超软地基排水板弯折特性与抗弯折结构

王海鹏，徐 杨，唐彤芝，吴月龙

(南京水利科学研究院岩土工程研究所，江苏 南京 210024)

新近吹填淤泥含水率高，几乎无结构性和强度，经浅层无砂真空预压处理3～4月，沉降压缩率可达到25%～35%[1-4]。处理后开挖常发现排水板存在较明显的弯曲(折)现象。相关专家学者在超软土及其处理技术方面开展了大量的研究[5-9]，围绕竖向排水板弯折对纵向通水量、真空度传递与损失、孔隙水渗流与土体强度增长影响等方面，关注于机理与影响效果开展了试验研究和理论分析，取得了较有意义的成果[10-13]。

本文基于压杆弯曲和管道恒定流的假设，分别从结构力学和流体力学的角度对排水板的弯曲变形及纵向通水量进行了理论计算分析；通过真空预压模型试验测试了人为弯曲状态下排水板板芯真空度与淤泥土体中孔隙水压力的分布特点；基于废弃料的利用提出了新型肋板结构，对其抗弯折能力和改善排水固结的实际功效进行了理论计算、工程应用和现场测试分析。

1 竖向排水板弯折的理论分析与模型试验

1.1 基于压杆弯曲的竖向排水板简化受力分析

以单根竖向排水板为对象进行分析。竖向排水板长细比很大，如板长3 m的B型板，长细比达到30，竖立于几乎呈流动状、强度几乎为零的超软淤泥中，排水板存在可以产生弯折变形的侧向空间。排水板的弯折变形主要与超软淤泥的大变形固结有关，是板-土相互作用的必然结果，其发展过程与淤泥结构性强度的增长有关，其弯折成因可基于细长压杆的弯曲理论[14]并结合必要的假设进行解释。

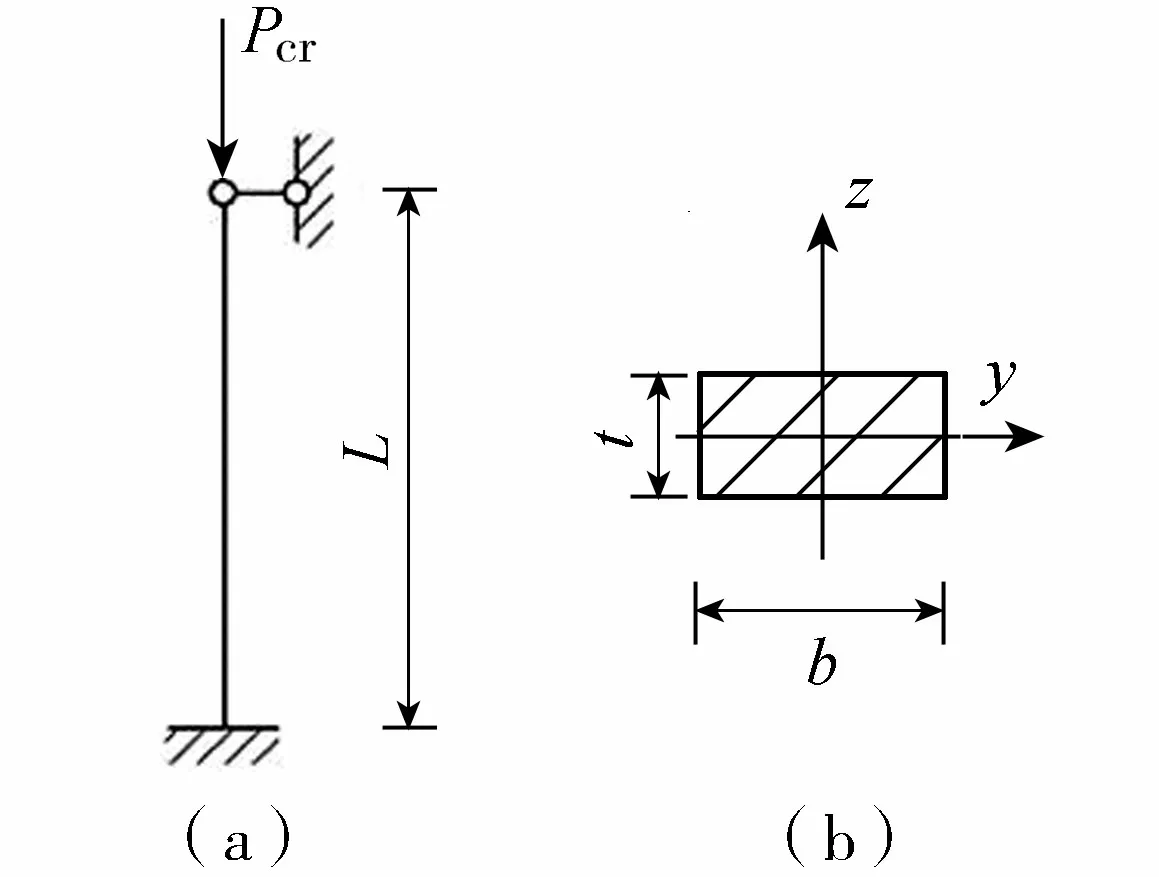
图1 排水板杆端支撑方式与受力简图Fig.1 Schematic diagram of support mode and force on rod end of drainage plate

理论而言，板侧淤泥对板的作用力呈对称性，相互抵消为零。工程实践中板顶端一般用扎绳缠绕紧裹于水平排水波纹管上，或采用专用直吸式接头与水平排水管连接，板顶端可视为允许竖向变形而不能侧向位移的铰支端，而板底端一般插入下卧硬土层，可视为不能产生竖向和侧向位移或转动的固定端。经简化基于压杆弯曲的单板受力分析见图1。

以B型塑料排水板为例，取弹性模量E=1 500 MPa，厚度t=4 mm，宽度b=100 mm，插设于地基中的板长L=3 m，根据文献[14]计算得到欧拉临界力Pcr=1.79 N。假定密封膜面平整，单根竖向排水板的顶端面范围内均受到抽真空产生的内外大气压力差80 kPa的作用，则得到理论作用力约为32 N，远大于Pcr，可见插设在超软淤泥地基中的竖向排水板在很小的作用力(外部荷载)下很容易产生弯曲变形。

1.2 基于管道恒定流排水板弯折通水量的理论计算

塑料排水板由齿槽状平板外包覆滤膜构成，在外侧受压的截面通水试验中可假设单个齿槽的水流形式为管道恒定流，其截面通水量Q可依据文献[15-16]进行计算。

定义塑料排水板试样弯折率K为

(1)

式中：H为原始试样长度，m；H′为弯折后试样长度，m。

考虑塑料排水板未弯折、S型弯折和Z型弯折3组类型分别进行纵向通水量理论计算分析： ①S型弯折曲率半径R分别取30 cm、35 cm、40 cm；②Z型弯折折角α′分别取60°、90°、120°。假设折弯段垂直距离为120 cm，原始试样H=400 mm，试验时的水力梯度宜为0.5，上下游水位差为0.2 m。

B型塑料排水板板宽100 mm、厚4 mm，单面共有31个齿槽，双面共有62个。单个齿槽尺寸为3.2 mm×2.0 mm，等效直径d=2.86 mm。板体截面Q≥25 cm3/s，单个齿槽Q=0.4 cm3/s。根据计算结果绘制不同弯曲率下排水板截面通水量的变化曲线，见图2。

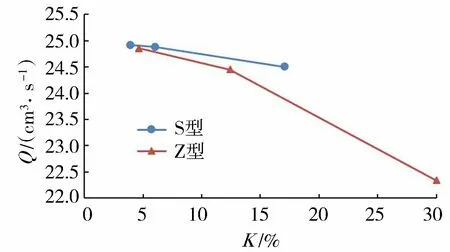
图2 排水板弯折率与截面通水量计算值的关系曲线Fig.2 Relationship curves between bending rate of drainage plate and calculated value of sectional water flow

由图2可见，Z型弯折对于截面通水量的影响要大于S型弯折。随着弯折率的增大，截面通水量明显减少。一般情况下抽真空时竖向排水板缓慢弯曲而不弯折时对其纵向通水能力影响较小，而急剧折角后排水板面上齿槽倒伏，排水通道受阻，通水量将显著减小。

上述计算可定性为反映弯折对纵向通水量的影响，但不能完全代表实际工况。插设在超软淤泥地基中的竖向排水板受力变形情况复杂，甚至可能会出现多处弯折甚至是扭折，对纵向通水量的影响很大。

1.3 竖向排水板弯折影响的模型试验

采用3个大小尺寸相同的油桶开展模型试验，每个油桶中预先插设2根人为弯折好的B型塑料排水板(弯折率分别为10%、20%和30%)。选择一根排水板,板芯内埋设深层真空度测头，深度为泥面以下0.4 m，在同一深度的两根排水板中间埋设1只孔隙水压力计。向油桶中灌注人造泥浆以模拟吹填超软土，3个油桶均连接同一吸水主管和一台7.5 W真空泵。管路连接后持续抽真空近1个月，监测真空度与孔隙水压力计读数，绘制相关变化曲线见图3～6。

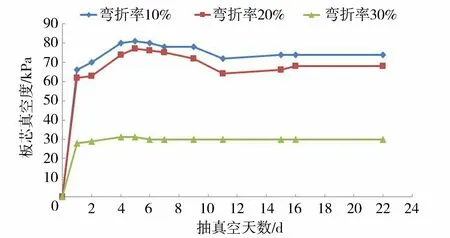
图3 板芯真空度的实测曲线Fig.3 Measured curves of vacuum degree of plate core

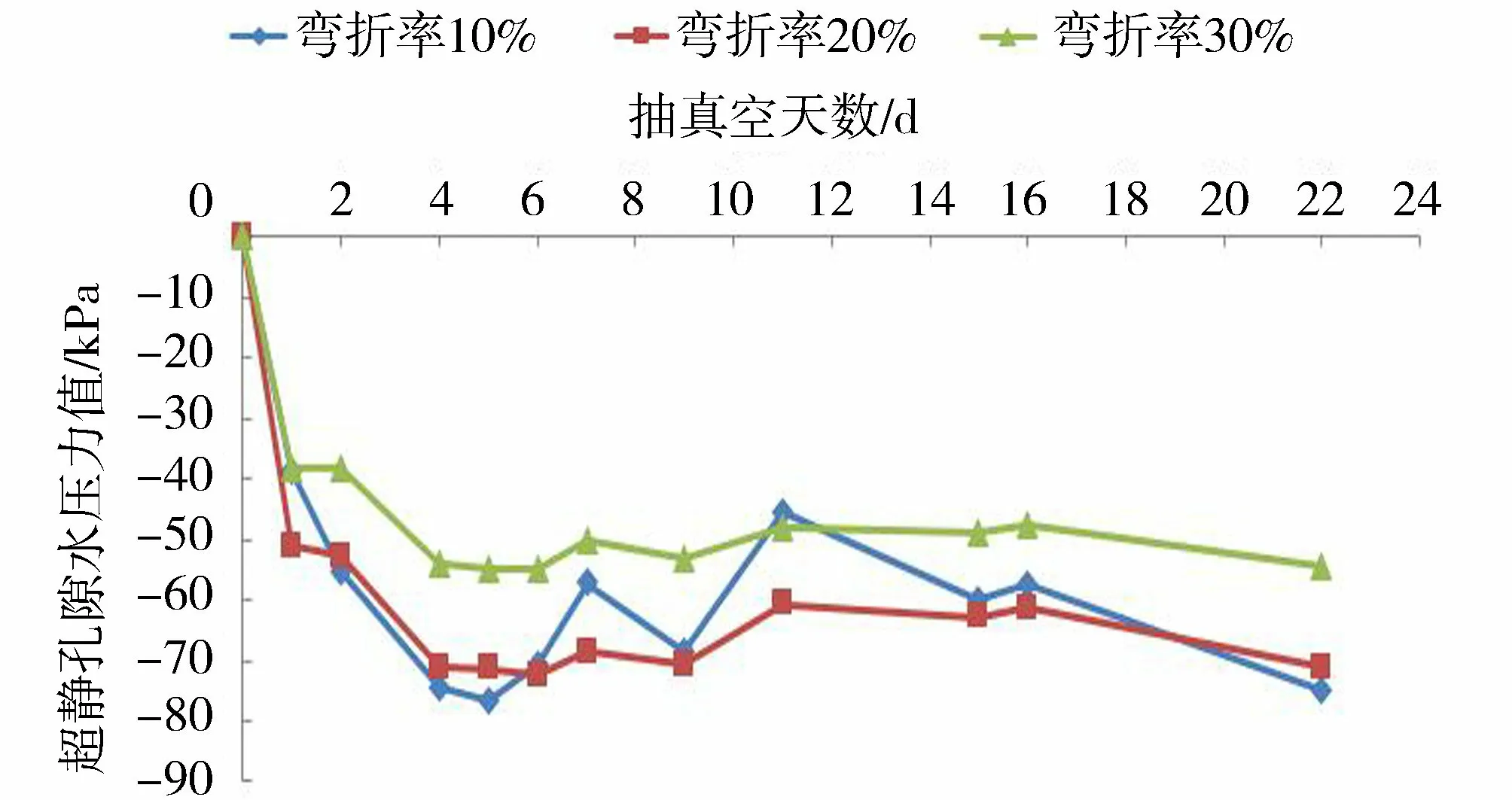
图4 淤泥中超静孔隙水压力的实测曲线Fig.4 Measured curves of excess pore pressure in silt

图5 排水板弯折率与板芯真空度的散点分布Fig.5 Scatter distribution diagram of bending rate and core vacuum degree of drainage plate

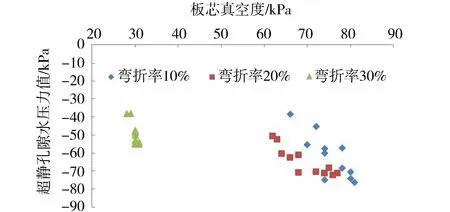
图6 板芯真空度与超静孔隙水压力的散点分布Fig.6 Scatter distribution diagram of core vacuum and excess pore pressure

试验结果表明：①竖向排水板弯折对真空度的传递和淤泥中超静孔隙水压力产生了比较明显的影响，弯折率越大，板芯真空度越小，抽真空时淤泥中产生的负的超静孔隙水压力值越低，不利于超软淤泥的排水固结。②由图5可见，弯折率由10%增加到20%，板芯真空度降低幅度为3～8 kPa，平均为5.6 kPa。弯折率由20%增加到30%，板芯真空度降低幅度为34～46 kPa，平均为39.6 kPa。由图6可见，弯折率为10%和20%时，板芯真空度与淤泥中的超静孔隙水压力构成的散点基本集中在一起，弯折率为30%时的散点则与弯折率为10%和20%时的散点明显拉开距离。弯折率对真空度传递的影响过程是非线性的，随着排水板弯折程度的不断加大，当达到某个弯折率时，其影响程度加剧，与图2反映的规律基本一致。

2 新型肋板结构的理论分析

2.1 基于废料利用的新型肋板结构

利用施工现场废弃的零散排水板，裁剪成一定长度的短板，称之为肋板，按一定的间距交错装订在排水板两侧，构成肋板复合体，一同插入淤泥地基中。新型肋板结构及现场布置见图7。

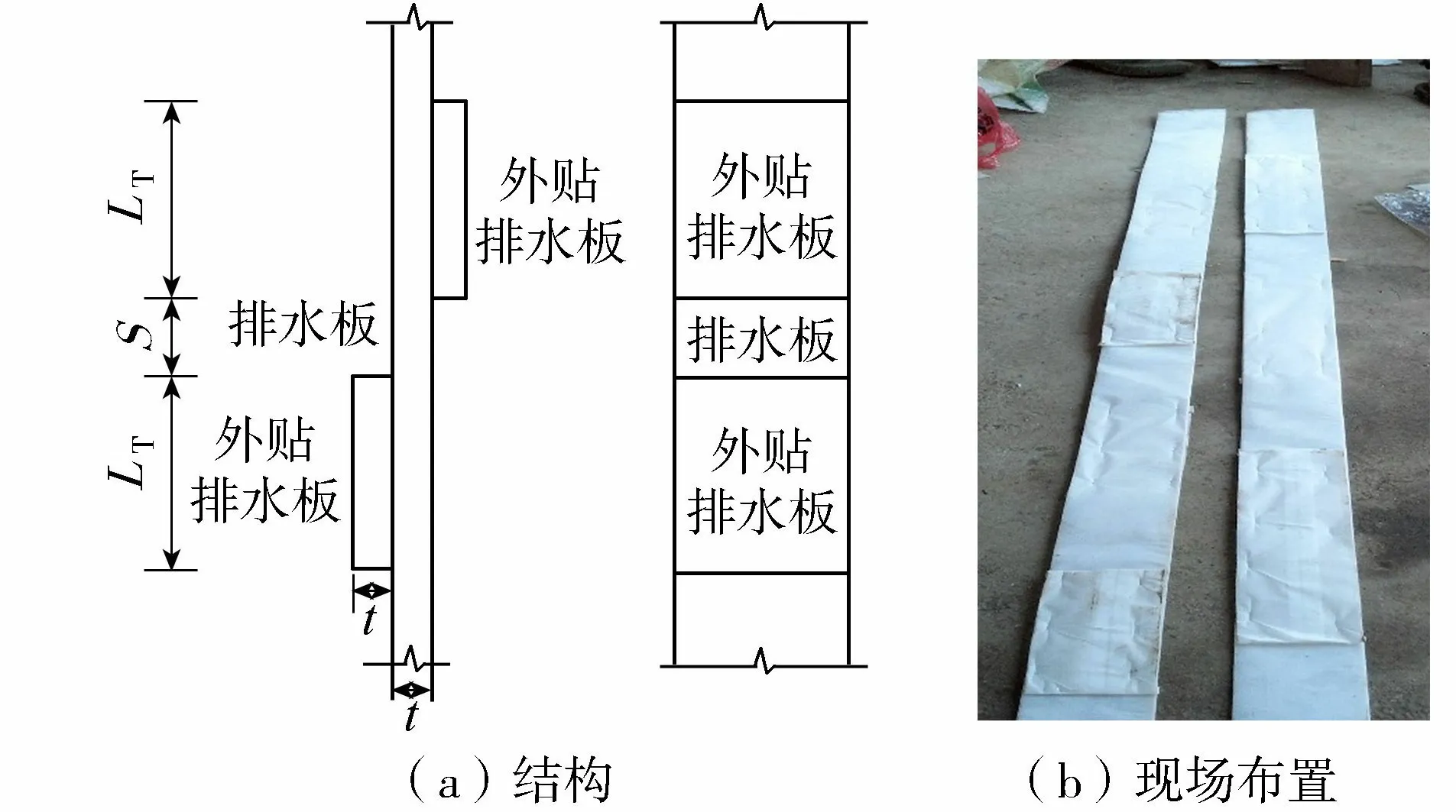
图7 新型肋板的排水板结构及现场布置Fig.7 Structure and in-situ configuration of drainage plate with new ribbed plate

2.2 新型肋板结构的截面抗弯刚度分析

截面抗弯刚度以材料的弹性模量E与构件横截面绕其中性轴惯性矩I的乘积表示。依据文献[14]对新型肋板结构未贴合段和贴合段的截面抗弯刚度进行计算。计算结果表明，采取加筋肋板措施后贴合段厚度增加一倍，而截面抗弯刚度则是未贴合段截面抗弯刚度的8倍。

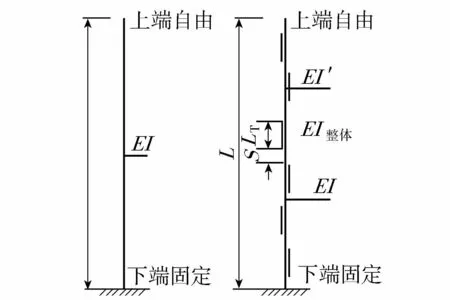
图8 两种板体结构整体稳定性计算简图Fig.8 Calculation diagram of overall stability of two plate structures

2.3 新型肋板结构的整体抗弯刚度分析

将插设于淤泥中的塑料排水板简化为下端固定、上端自由的轴心受压构件，按图8对原单板及新型肋板结构排水板的整体抗弯刚度进行计算。

单板欧拉临界力计算见文献[14]，新型肋板结构排水板的抗弯刚度EI整体根据肋板段和无肋板段的长度分配，分别采用不同的截面抗弯刚度进行加权平均计算，可得到：

(2)

式中：L1为肋板段的总长度，m；L为排水板的总长度，m。

由式(2)可得EI整体≥EI，肋板段的总长度越大，结构整体抗弯刚度越大，且数倍于原排水板，大大增强了新型肋板结构排水板的整体稳定性和抗弯折能力。

2.4 肋板布置方式及参数分析

综合考虑现场废弃料的有效利用和增强板体抗弯折能力两个方面，认为采用一定长度的肋板分别在排水板两侧按一定间距进行交错布置的方式比较合理。结合上述理论分析，肋板是排水板的抗弯增强体，板体抗弯刚度主要取决于肋板总长度及布置方式，肋板长度和排列间距是施工布设时需考虑的两个重要参数。

考虑加筋肋板板体结构的受力连续性，单板整体的临界力Pcr(整体)、肋板贴合段临界力Pcr(肋板段)和无肋板段临界力Pcr(无肋板段)三者理论上相等， 即

(3)

单板整体可视为顶端铰支、底端固定，其长度系数μ整体可取为0.7，而肋板段和无肋板段可视为两段铰支，其长度系数取μ肋板段=μ无肋板段=1.0。于是可得到肋板长度LT与间距S之间最佳的理论关系为：LT=2.828S。

在L一定、满足整体抗弯能力的情况下，可适当调整肋板长度与排列间距的大小，以便于现场操作并提高废弃料的有效利用率。

3 新型肋板结构排水板的现场试验

3.1 工程概况与试验方案

苏州某清淤工程排泥场堆放新近吹填淤泥，厚度3 m左右，测试天然堆置状态下吹填土的含水率为122.8%，塑性指数为21.9，粉粒和黏粒的细颗粒含量为75.5%，为典型的超软、高含水量细颗粒黏性土。采用逐步加载的无砂真空预压法进行地基处理，人工插设B型排水板，深度3 m左右，正方形布置，间距0.8 m。利用场地内原有隔堤并考虑施工方便划分为7个区。其中6区面积约1.6万m2，距吹填口最远、泄水口最近，处于吹填淤泥沿流道自然落淤的末端。该区于2014年6月初开始抽真空，监测显示淤泥地基固结状态正常。进入7月后现场检查发现一块区域(长宽均约20 m)的泥面明显软于四周场地，密封膜松软，经多次重点加抽后未能有效。揭膜后发现，泥面积水明显，仍呈强度很低的流塑状，表明该区域的排水系统基本失效。因此，选择该薄弱区域，重新插设新型肋板结构的排水板进行现场试验研究。

在试验区原有两排排水板中间，按间距0.8 m补插新型肋板结构的B型塑料排水板，板长2 m。利用现场废弃料按两种长度裁剪制作肋板，按间隔20 cm正反交错装订于母板上。方案 T1的肋板长度为40 cm，肋板数量为3个，方案 T2的肋板长度为30 cm，肋板数量为4个。新型肋板结构现场施工情况见图9。两个方案的肋板总长均为120 cm，根据式(2)可知两种方案的板体抗弯刚度相同，肋板长度和数量不同。

图9 新型肋板结构现场施工图Fig.9 Field construction of new ribbed plate structure

试验区布设了真空度(板芯内深度0.5 m、1.5 m处)、孔隙水压力(泥面以下1 m地基土)、表层沉降(试验区中间的泥面)监测。排水板补插完毕后，恢复原场地的土工布及2层密封膜，重新开始抽真空，并与大区抽真空保持一致。

3.2 现场监测与效果分析

3.2.1 真空度

对试验区埋设的水平波纹管内、膜下以及板芯不同深度的真空度进行监测，绘制真空度实测变化曲线如图10所示。由图10分析可知，真空压力从水平波纹管内向膜下泥面和地基板内传递过程中出现明显衰减，水平管内(最大值80 kPa，最小值72 kPa，平均值77.9 kPa)与膜下泥面(最大值78 kPa，最小值70 kPa，平均值74.6 kPa)衰减程度较小，沿板芯向地基板内传递的衰减幅度较大。实测板芯深层真空度：T1方案为0.5 m深度处平均值为57.1 kPa，1.5 m深度处平均值为48 kPa；T2方案为0.5 m深度处平均值为55.7 kPa，1.5 m深度处平均值为51.4 kPa。板芯0.5 m处真空度平均值为55.7～57.1 kPa，约为膜下真空度的69.6%～71.4%，板芯1.5 m处真空度平均值为48.0～51.4 kPa，约为膜下真空度的60.0%～64.2%。

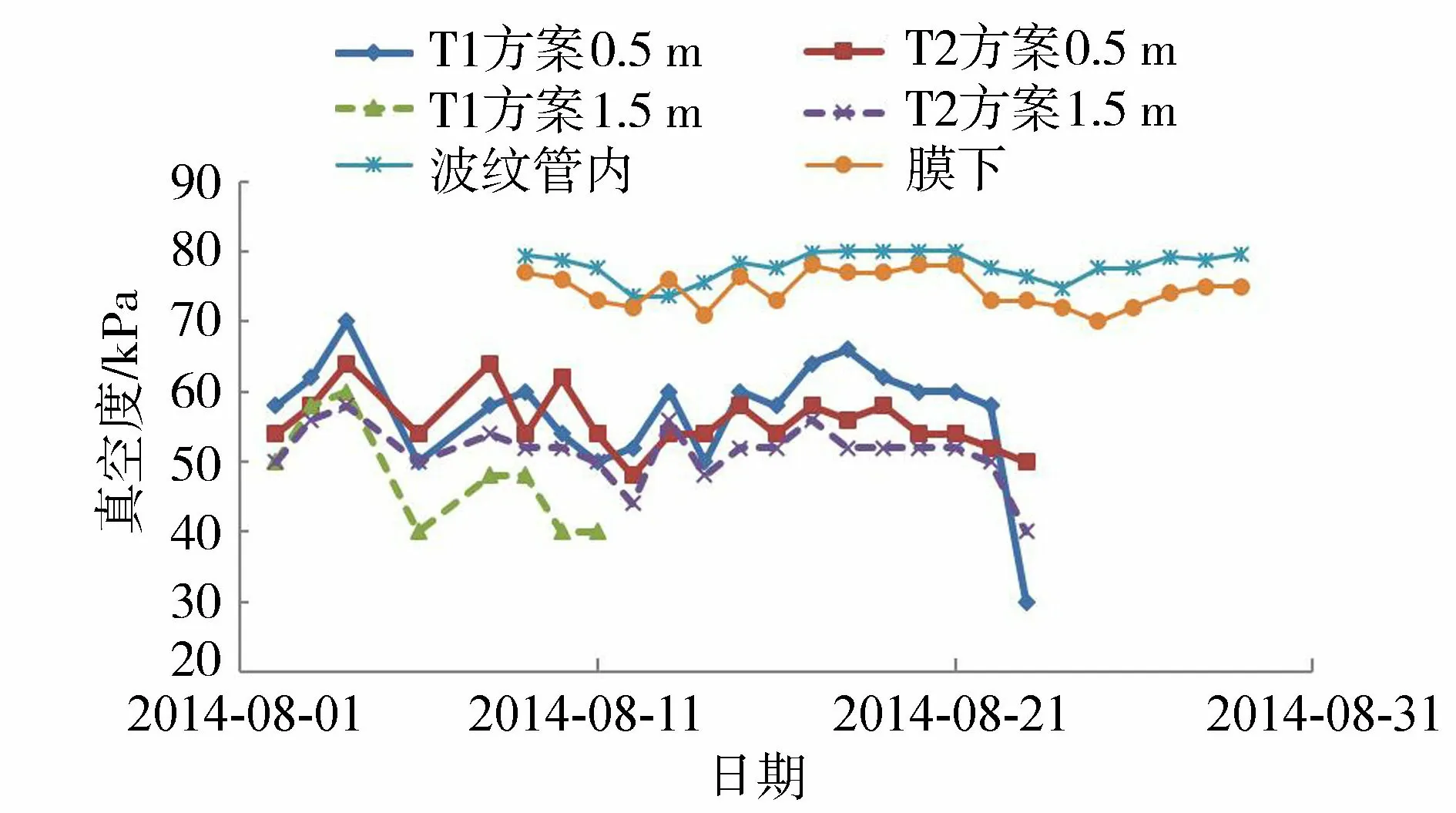
图10 真空度实测曲线Fig.10 Measured curves of vacuum

排泥场的2区、4区、5区沿深度也进行了板芯真空度监测，每个区域选择2根或3根竖向排水板，每根排水板沿板芯布设4个真空度测头，发现实测真空度均很低，基本没测到几次读数(故无法整理出有意义的曲线和数据)。对比表明，同样条件下，在B型板两侧按一定间距交错贴合废料短板，通过局部加筋增强的方式提高了排水板的整体抗弯折能力，一定程度上改善了真空压力的深层传递效果。通过现场试验还可以发现，在板芯埋设真空度测头，测头通过细小软管穿越板体与外面的真空表连接，细小软管铺设于滤布与板芯齿槽之间，这种目前常用的深层真空度监测方法虽然直观简便，但在超软淤泥地基中受到排水板易淤堵和弯折变形的影响，监测寿命较短，往往难以获得长系列的实测数据。

3.2.2 孔隙水压力

图11为抽真空期间1 m深度处超静孔隙水压力随时间的变化曲线。由图11可见，抽真空后淤泥地基内的孔隙水压力值减小速度较快，超静孔隙水压力曲线几乎呈线性陡状发展，表明重新插设带有肋板结构的排水板后，地基的排水固结体系得到改善和恢复，淤泥的排水固结状态较好。

抽真空期间(8月3—29日)T1和T2方案产生的孔隙水压力最大变化量(超静孔隙水压力值)分别为-11.4 kPa、-23.0 kPa，T2方案的负超静孔隙水压力值大于T1方案，停抽后T2方案的超静孔隙水压力消散也明显快于T1方案，与图7两个方案测得的深层真空度变化规律具有一定的相关性。就总体平均而言，T2方案测得的深层真空度比T1方案数值大、持续平稳性好。

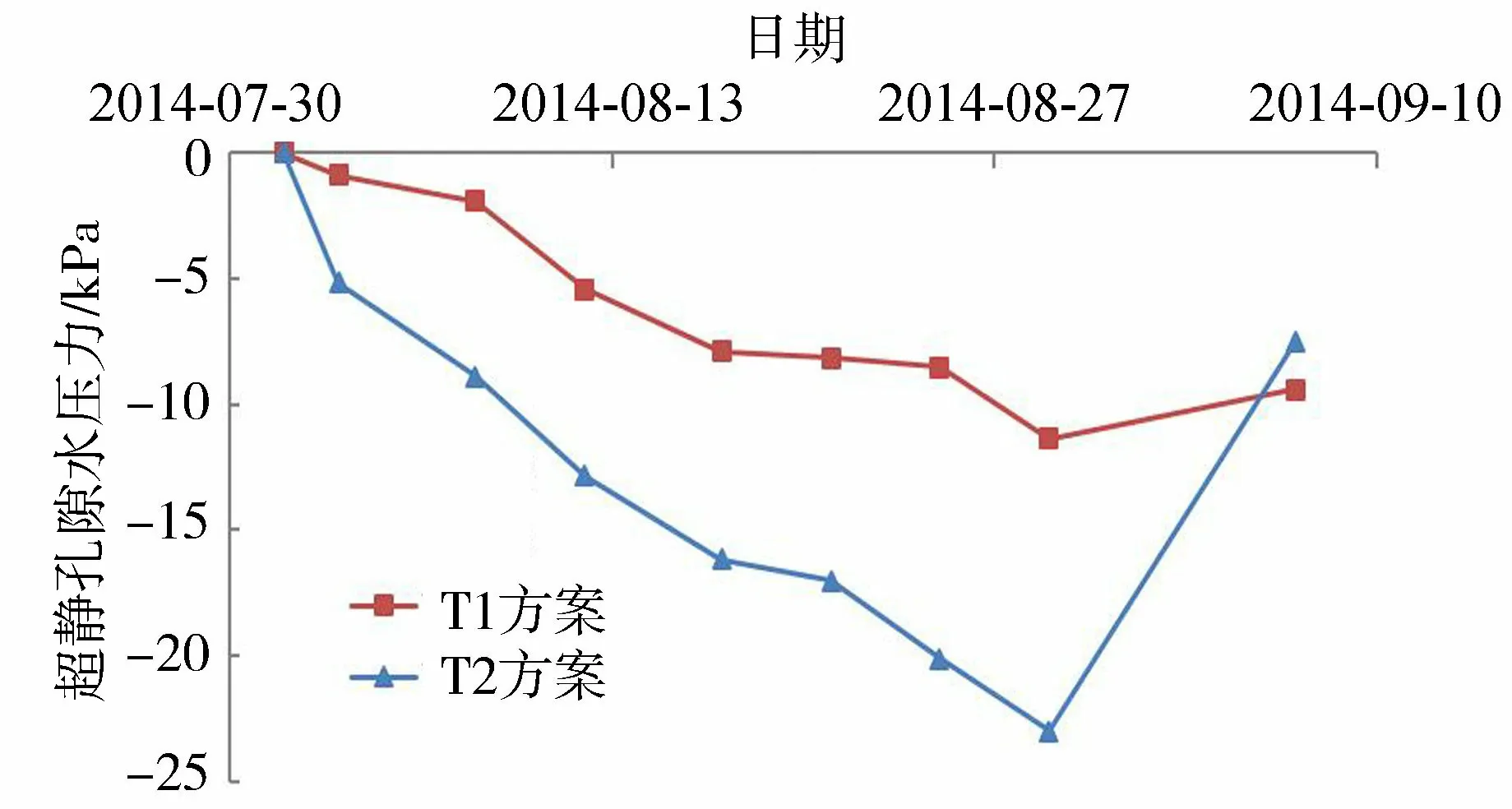
图11 泥面以下1 m处超静孔隙水压力变化曲线Fig.11 Variation curves of excess static pore pressure at 1 m below the mud surface

T1、T2两个方案的板体抗弯刚度相同，但肋板长度和数量不同，T2方案排水板两侧各两个肋板；T1方案排水板一侧两个肋板，另一侧一个肋板。通过对比两个方案在参数设计上的差异来初步定性分析导致真空度和孔隙水压力分布方面存在差异的原因：采用简单的装订贴合方式，肋板贴合段虽然提高了抗弯刚度，但同时在一定程度上肋板对贴合侧的渗流排水通道产生了不利的堵塞作用。T2方案肋板长度短，但数量多一个，且为偶数，通过交错对称布设可知，该方案的无肋板未贴合段的数量比T2方案多一个，则肋板的整体堵塞作用弱于T1方案，故整体有利于真空压力的传递和土体孔隙水的渗流排出。考虑到试验方案本身的局限性，用于对比的测试数据较少，本文的分析仅供参考，其合理性尚待进一步研究。

3.2.3 泥面沉降量分析

图12为试验区泥面沉降实测曲线，将近1个月的持续抽真空产生的累计沉降量为414 mm，抽真空12 d时的日沉降速率最大(27 mm/d)，停抽8 d后实测沉降量略有回弹，回弹量约为10 mm。实测累计沉降量曲线基本呈线性增长，发展平稳且波动性小。图13反映出地基土体的超静孔隙水压力与沉降变形之间存在良好的相关性。说明重新插设新型肋板结构排水板，通过提高竖向排水板抗弯折能力，改善了淤泥地基真空压力和孔隙水压力的时空分布状态，促进了土体的排水固结。

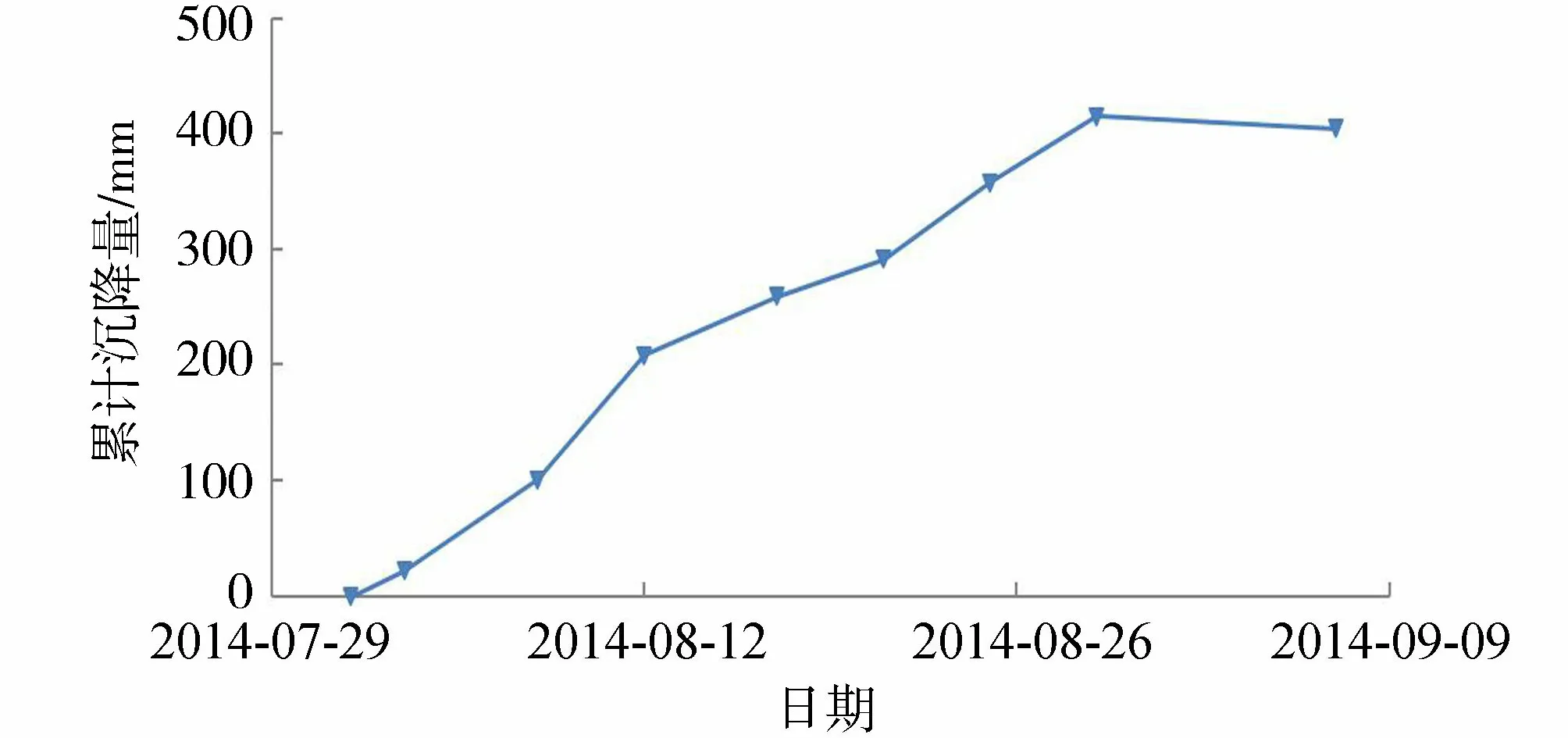
图12 泥面沉降变化曲线Fig.12 Variation curves of mud surface settlement

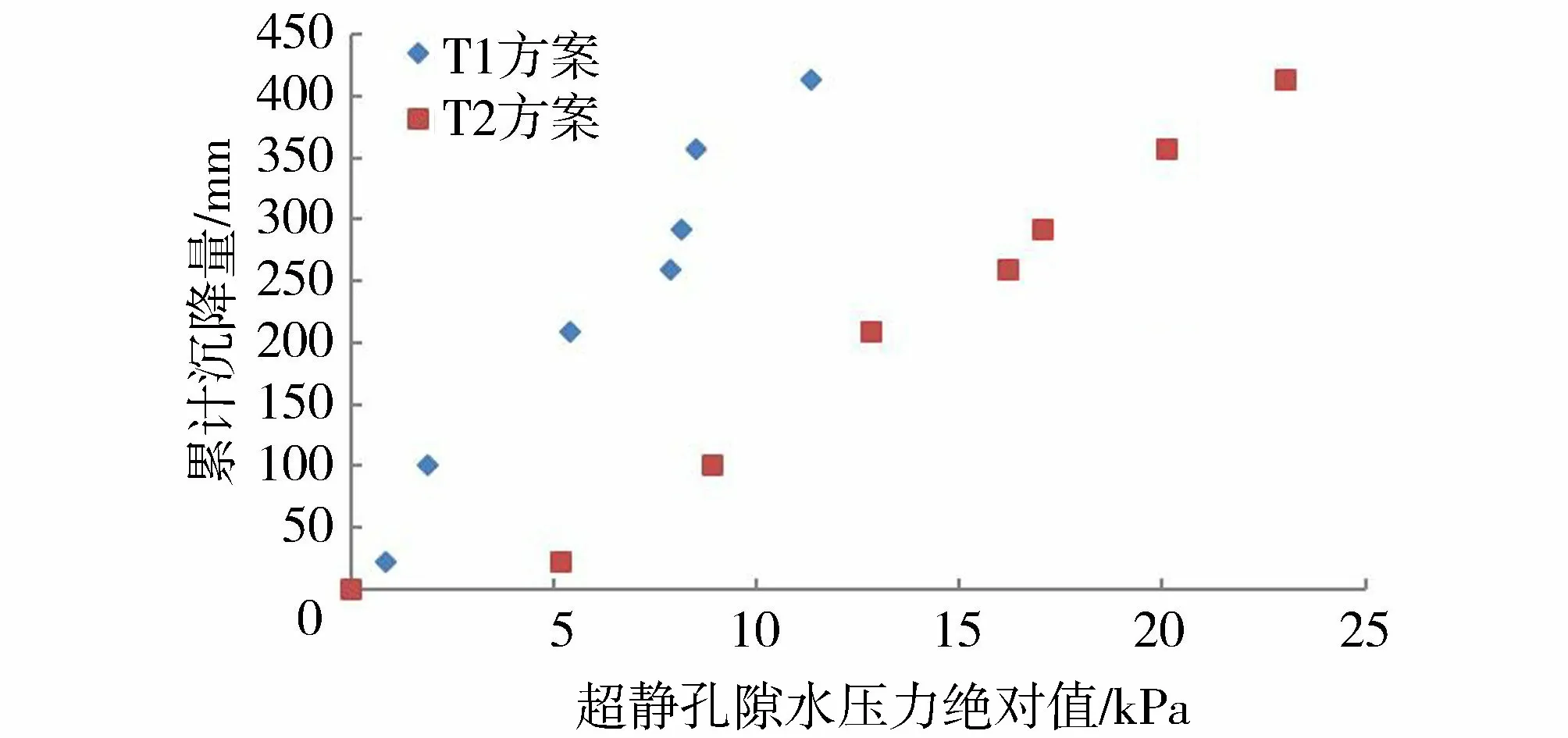
图13 泥面累计沉降量与超静孔隙水压力绝对值散点分布Fig.13 Scatter distribution diagram of cumulative settlement and absolute excess pore pressure

3.2.4 效果检验分析

抽真空完成后揭膜进行场地开挖。由图14可见泥面干燥硬实，土体内的排水板整体保持直立形状，总体反映了新型肋板结构的抗弯折能力强，可以有效适应超软淤泥地基的固结大变形。在肋板贴合段的接头处存在弯折现象，可能是由于肋板段与无肋板段之间的刚度差异和接头处两边板体受到的侧向摩擦力产生的局部附加弯矩造成的。

图14 抽真空结束后试验区现场开挖实景Fig.14 Actual scene of excavation in the test area after vacuuming

在6区场地选择6处进行十字板剪切强度测试，其中6号测点位于试验区内，整理测试结果见图15。由图15可见，经真空排水预压固结处理后，超软淤泥的强度得到了大幅度提高，处理前剪切强度Cu值几乎为零，处理后十字板剪切强度Cu值达16～23 kPa，试验区土体强度与其他区域基本相当。采用土层各深度处十字板剪切强度值的小值平均值乘以3.14作为整个土层的平均容许承载力[16]，推算得到加固后吹填淤泥土体的地基承载力为52.8～55.6 kPa。静载试验结果表明，场地内两处泥面地基承载力特征值分别为60 kPa和63 kPa，平均值为61.5 kPa，与十字板测试结果基本相当。检验结果均满足设计要求(不低于50 kPa)。

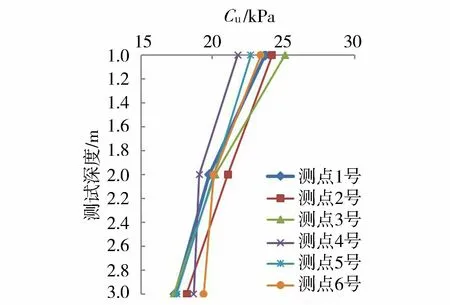
图15 抽真空结束后十字板剪切强度试验曲线Fig.15 Curves of cross plate shear test after vacuuming

3.3 效益分析与评价

在超软吹填淤泥中人工插设排水板，裁减后会产生单根长度不够的边角料，即成为废弃料，不同的排水板施工参数产生的废弃边角料数量不同。根据本文实例，排泥场处理面积共约8.6万m2，正方形插设排水板，间距0.8 m，单根长度3.3 m(平均插设深度3.0 m，另加缠包水平管的排水板长度0.3 m)，则塑料排水板总用量约为41 250 m，排水板单捆包装一般为200 m/捆，需206捆。每捆可裁剪成60根用于人工插设的单板，剩余2 m成为再次利用的边角料，再加上一些难以避免的损耗，初步估算该工程产生的边角料数量为排水板设计用量的1%以上。若利用这些废弃料做成新型肋板以提高竖向排水板的抗弯折能力，用于浅层局部薄弱区域以增强地基的排水固结功效，简单实用，既达到技术目的，又实现了废弃料的有效利用，技术经济性较好。

4 结 论

a.基于压杆弯曲的假设对竖向排水板进行受力计算，得到插设在超软淤泥地基中的排水板在很小的外部荷载作用下即可产生弯曲变形的结论。基于管道恒定流的假设计算分析不同的弯折形状和程度对通水量的影响，表明Z型弯折的通水量明显小于S型弯折，弯折率越大，通水量越小。

b.通过模型试验对人为弯折状态下排水板板芯真空度与淤泥土体中孔隙水压力的分布进行了测试，发现排水板弯折对真空度的传递和淤泥中超静孔隙水压力产生了明显的影响，弯折率越大，板芯真空度越小，淤泥中产生的负超静孔隙水压力值越低。弯折率由10%增加到20%，板芯真空度降低幅度为3～8 kPa，平均为5.6 kPa。弯折率由20%增加到30%，板芯真空度降低幅度为34～46 kPa，平均为39.6 kPa。弯折率为10%和20%时，板芯真空度与淤泥中的超静孔隙水压力构成的散点基本集中在一起，弯折率30%时的散点则与弯折率为10%和20%时的散点明显拉开距离。可见弯折率的影响是非线性的，随着弯折程度的不断加大，当达到某个弯折率时，其影响程度加剧。

c.基于废弃料的利用提出了新型肋板结构，对其抗弯折能力和改善排水固结的功效进行了理论计算和现场试验研究。新型肋板结构的截面抗弯刚度是普通板的8倍，板体抗弯刚度视肋板贴合的总体长度可提高数倍以上。加固后开挖板体基本呈直立状态，吹填土体十字板剪切强度达16～23 kPa，地基承载力特征值达60～63 kPa，满足设计要求。新型肋板结构可增强排水板抗弯折能力并改善排水固结效果，简单实用，实现了废弃料的有效利用，具有较好的技术经济性。

d.受条件限制，本文开展的新型肋板结构现场试验具有一定的局限性，主要表现为：试验区不是独立设区，而是大区里的局部薄弱区域，面积小，试验参数比较单一。在前期抽真空几乎无效的情况下重新揭膜补插肋板复合体，再与大区一起覆膜抽真空，因此试验区的真空压力场、渗流场分布不是完全独立的。

e.本文提出的肋板理论长度约为排列间距的2.828倍，应用时应综合考虑提高整体抗弯能力的技术性和有效利用现场废弃料的经济性进行适当调整，当板长一定时建议采用“数量多(偶数)的短肋板”方案。