邯郸市永年区不同PM修正模型麦田蒸散模拟对比

周 炜，王洪峰，栾清华，高 翔，张海生，王利书

(1.河北工程大学河北省智慧水利重点实验室，河北 邯郸 056038；2.邯郸市气象服务中心，河北 邯郸 056005； 3.河海大学农业科学与工程学院，江苏 南京 210098)

农田蒸散(evapotranspiration，ET)是农田作物蒸腾和土壤蒸发的总和，是土壤-植物-大气系统(soil-plant-atmosphere continuum，SPAC)中水分交换的关键过程[1]，也是可同时影响农田水量平衡过程和能量平衡过程的唯一要素[2]。农田蒸散的模拟和观测一直是农田水利学、水文学、土壤学、生态学、气象学等相关学科的重要研究内容，对于农田旱情监测、节水灌溉、提高作物水分生产力有重要的意义[3]。目前，农田蒸散测定方法主要有水量平衡法、光合作用仪法、热量法、蒸渗仪法、涡度相关法、波文比-能量平衡法、大孔径激光闪烁仪法、遥感法等[4-6]；农田蒸散模拟方法有Penman-Monteith(PM)模型法[7-9]、Shuttleworth -Wallace(SW)模型法、Clumping(C)模型法等[4]。其中，PM模型是1965年Monteith在Penman模型[5]考虑能量平衡和水汽扩散理论的基础上，引入冠层阻力建立的估算蒸散的模型[10]；之后，因其较明确的物理理论依据、较高的计算精度和较强的适用性成为在蒸散研究中应用最多的模型[11]。然而，该模型在计算下垫面蒸散时，未区分土壤蒸发和植株蒸腾，将其概化为一个单源大叶蒸腾模型[12]。显然，在农田自然生态系统中，即使作物封垄，作物蒸腾成为总蒸散的主要分量，土壤蒸发仍然不可忽略[13]。因此，研究者们为提高模拟精度，应用不同原理考虑并添加土壤蒸发，形成了不同形式的PM修正模型，其中比较经典的有基于分割可用能量为冠层吸收和土壤吸收的PM修正模型[14-16](简称PM-1模型)，基于分割地表为块状的冠层覆盖和土壤裸露的PM修正模型[12](简称PM-2模型)，使用双作物系数法，基于分割单作物系数为基础作物系数和土壤蒸发系数的PM修正模型[17](简称PM-3模型)。

以往有关蒸散模型的模拟效果对比较多关注于不同模型之间的对比，如张方敏等[18-21]对PM、Hargreaves、Makkink、Priestley-Taylor等不同蒸散模型进行了对比，结果表明PM模型具有较强的适用性；而同种模型不同修正结构下的模拟效果对比关注较少。由于不同类型的PM修正模型计算原理不同，同一条件和区域的蒸散模拟结果必然存在差异，而其在不同区域、不同农田下的适用性需要进一步研究。

本文以邯郸市永年区为研究区，基于区域农田种植现状，在空间上选择多个典型试验麦田，采用PM-1模型、PM-2模型和PM-3模型分别模拟冬小麦关键生长期农田的蒸散并以麦田水量平衡结果为参照，检验蒸散模拟的效果，以期为科学管理农田水分、制定合理灌溉制度提供参考。

1 研究区与数据采集

1.1 研究区概况

河北省邯郸市永年区(36°35′N～36°56′N，114°20′E～114°52′E)位于邯郸市主城区的北部及东北部(图1)，辖17个乡镇，总面积761.72 km2。全区地势西高东低，西部为低山丘陵，东部为平原；属温暖带半湿润大陆性季风气候，多年平均降水量为520 mm左右，年平均气温为10～21℃，年平均日照时数为2 464 h，年平均相对湿度为67%，雨热同期，利于农业粮食生产发展。经调研，永年区内耕地面积为5.29万hm2，占整个永年区面积的69%，且绝大多数为冬小麦-夏玉米轮作，一年两熟，其分布见图1(a)。灌溉方式主要是地下水井灌，少部分采用地表渠灌。综上，永年区在气候条件、作物轮作及灌溉制度方面均具有邯郸市县域的典型特征，故选取永年区为研究区，并在中东部9个乡镇的10块典型麦田开展研究。选取的麦田基本信息如表1所示，位置分布如图1(b)所示，10块麦田的土壤质地为粉砂质壤土或粉砂质黏壤土，均为冬小麦-夏玉米轮作，在关键生长期内均井灌1～2次，且灌溉时间总体较为一致，这些均具有永年区农田耕作管理的普遍特性。

图1 研究区麦田分布Fig.1 Distribution of wheat fields

1.2 数据采集与计算

1.2.1 土壤含水量数据

土壤含水量数据采集依托连续的现场土壤墒情试验。为更好地获取不同空间的区域农田蒸散分布特征，根据区域冬小麦种植分布(图1)情况，使用TRME-PICO-T3 TDR剖面土壤水分测量系统(包含传感器、读表、测管)于冬小麦关键生长期即2019年4月16日至5月27日对表1所示的10块试验田进行监测，监测频次为2日一测。依据文献[22]中有关华北地区冬小麦关键生长期主要根系分布在1 m深度的研究成果，监测深度为0～90 cm，分7层(0～10 cm、10～20 cm、20～30 cm、30～40 cm、40～50 cm、50～70 cm、70～90 cm)测量。监测仪器精度为±0.01%，为校验仪器，在监测前人工土钻采集10～20 cm、30～40 cm、50～70 cm层的土样，另采用称重烘干法获取含水量数据并与仪器监测同期数据进行比对。比对结果表明，监测数据较称重烘干数据相对误差低于5%，说明该仪器适用于永年区开展土壤墒情监测。

表1 试验田基本信息

1.2.2 关键土壤水分参数

田间持水量(θFC)和凋萎含水量(θWP)是PM模型对比分析中较为关键的两个土壤水分参数，也是两个比较抽象化的概念。选择环刀法获取土壤样品，开展土壤颗粒分析试验，获得土壤颗粒级配并进行经验估算。参考陈晓燕等[23-24]的研究结果计算各监测点的θFC和θWP：

θFC1=-2.353 3+0.069 26wsa+0.128 11wsi+1.694 26wcl

(1)

θWP=0.002 5wcl+0.033 9

(2)

式中：wsa为砂粒质量分数，%；wsi为粉粒质量分数，%；wcl为黏粒质量分数，%。为进一步减小不确定性，再将θFC经验公式[24]结果与式(1)进行比较：

θFC2=0.012 5wcl+0.023 2

(3)

1.2.3 气象和灌溉数据

气象数据采用永年气象站(站号为53895)日尺度实测数据，包括平均气温(T)、最高气温(Tmax)、最低气温(Tmin)、平均相对湿度(H)、最小相对湿度(Hmin)、10 m高平均风速(u10)、日照时数(n)以及降水量(P)。经实地调研，灌溉量数据可依据当地灌溉时长及管道出水流量计算，流量由流速仪测定。关键生长期温度、湿度及降雨灌溉量变化如图2所示。

图2 温度、湿度及降雨灌溉量Fig.2 Temperature, humidity, precipitation and irrigation

表2 冬小麦生育阶段划分、植被覆盖度及叶面积指数

1.2.4 作物生长指标

作物生长指标包括冬小麦生育阶段划分、植被覆盖度(fc)和叶面积指数(leaf area index，LAI)，如表2所示。生育阶段划分采用文献[25]的划分方式，LAI通过MODIS遥感影像提取(MOD13A1，产品数据是NDVI植被指数，空间分辨率为1 000 m，时间分辨率为16 d)。fc与LAI有较强的相关性，可通过关联公式经验推算：

fc=1.005[1-exp(-0.6l)]1.2

(4)

式中l为叶面积指数。计算结果与文献[25]基本一致。经多次调研，各监测点农民种植习惯较为一致，且整个监测期小麦生长差异较小。在各田内用卷尺人工测量5个2 m×2 m的代表点，并数出代表点内小麦株数以计算种植密度，结果显示种植密度差异并不显著。故概化监测期内各田的fc和LAI相同。生育阶段之间的作物生长指标采用线性内插。

2 模型与评价方法

2.1 PM模型法

2.1.1 模型基本原理

PM修正模型以Penman-Monteith公式为基础，是大叶假设下的单源结构形式，计算公式如下：

(5)

其中ra=208/u2

式中：E为蒸散量，mm；λ为蒸发潜热；Δ为饱和水汽压与温度曲线的斜率，KPa/℃；Rn为表面净辐射，MJ/m2；G为土壤热通量，MJ/m2；ρ为空气密度，kg/m3；CP为空气定压比热，MJ/(kg·℃)；es-ea为饱和水汽压差，KPa；γ为干湿表常数，KPa/℃；ra为空气动力学阻力，s/m；rc为冠层阻力，s/m；u2为2 m高平均风速。

PM模型模拟分直接计算和间接计算两种方式：①直接模拟蒸散时需要计算rc，可采用Jarvis等[26-27]提出的公式，即

(6)

其中F1=1.583Rn/(197.810 8+Rn)F2=(θ90-θWP)/(θFC-θWP)

F3=1-0.061(es-ea)F4=1-0.001 6(T0-T)2

式中：rmin为最小气孔阻力，对于冬小麦取85 s/m；le为有效叶面积指数，基于不同LAI的大小计算，采用李俊等[28]的研究结果；F1、F2、F3、F4分别为辐射[11]、土壤水分、空气湿度、温度影响因子；θ90为0～90 cm内的平均土壤含水量；T0为参考叶温，一般取25℃[28]。②间接模拟蒸散时不需要特别计算rc，直接采用FAO56定义下参考作物的rc=70 s/m，但需要进一步确定作物系数K。Δ、Rn等参数的确定可参考相关文献[29]。

2.1.2 模型修正策略

单源的结构形式不区分植被蒸腾和土壤蒸发，模型只在植被冠层郁闭的情况下模拟效果较好；双源的结构形式将冠层和土壤划分为两个相互独立又相互作用的源汇，将蒸散用植被蒸腾Ec和土壤蒸发Es之和表示，即

E=Ec+Es

(7)

通过进一步参数化的方式改善模型模拟效果。不同的参数引入和划分原理，产生PM模型不同的双源修正结构。

a.PM-1模型结构形式引入冠层透过率τ将可用能量分割为冠层利用的能量和土壤利用的能量，同时引入土壤蒸散系数f确定Es，从而将E分离为Ec和Es两部分[14]：

(8)

(9)

其中τ=exp(-kle)

式中k为辐射的衰减系数，设为0.6。τ根据Beer定律求解；f参考了文献[16]的研究结果。

b.PM-2模型结构形式引入fc将地表分割为块状，冠层覆盖地表利用rc确定Ec，土壤裸露地表引入参数土壤表面阻力rs确定Es，从而将E分离为Ec和Es两部分[12]：

(10)

(11)

其中rs=exp(8.4-5.9ms)ms=(θ10-θWP)/(θFC-θWP)

式中ms为土壤湿度指数，用θ10计算。

c.PM-3模型结构形式为双作物系数法的结构形式。区别于PM-1模型和PM-2模型，PM-3模型是蒸散的间接模拟模型，是单作物系数法的改进形式。PM-3模型结构形式引入基础作物系数Kcb和土壤蒸发系数Ke，将单作物系数K分割，从而将E分离为Ec和Es两部分[2]：

E=(KsKcb+Ke)E0

(12)

Kcb=Kc,min+Kcc(Kcb,full-Kc,min)

Ke=Kr(Kcb,full-Kcb)Kcc=1-exp(-kle)

式中：Ks为水分胁迫系数，等同于F2；E0为参考作物蒸散量；Kcc为冠层覆盖度系数；Kc，min为裸土最小作物系数，取0.1；Kcb，full为作物完全覆盖地表时的最大基础作物系数；h为冬小麦关键生长期平均高度，取1 m；Kr为土壤蒸发衰减系数，用θ10计算。

2.2 水量平衡法

冬小麦关键生长期的农田蒸散量利用水量平衡法计算[29]：

E=P+I-D+C±ΔW

(13)

式中：P为降水量，mm；I为灌溉量，mm；D为深层渗漏量，mm；C为地下水由毛管上升的水量，mm；ΔW为土壤水蓄变量，mm。考虑研究区冬小麦关键生长期主要根系分布的深度[22]及土壤含水量的测定情况，取ΔW的土壤层深度为90 cm。由于区域地下水埋深为20～60 m，考虑日尺度下90 cm土壤层深度范围内水量平衡的实际情况，D和C可忽略不计。

2.3 评价指标选取

从精度和分布均衡度两个层面选取指标评价PM-1模型、PM-2模型、PM-3模型的蒸散模拟效果。

a.精度评价以水量平衡法计算的2日蒸散量作为参照值，采用平均绝对误差(MAE)、均方根误差(RMSE)、标准均方根误差(NRMSE)、决定性系数(R2)、一致性指数(AI)及整体评价指标(GPI)[30-31]作为评价指标。平均绝对误差反映模拟值误差的实际情况；均方根误差反映模拟值与参照值之间的偏差；标准均方根误差是均方根误差的归一化处理，指标越小表示模拟效果越好；决定性系数和一致性指数分别反映模拟值与参照值之间相关性是否显著和离散程度及相对偏差；整体评价指标是对上述指标的综合处理，针对各指标的不同反映层面与优势进行最后的综合评价，指标越大表示模拟效果越好。

b.分布均衡度评价采用信息熵指标，可描述和判断蒸散在分布上的有序与无序、规则与杂乱、均匀与悬殊，公式可参考文献[32]。计算10块麦田关键生长期内2日蒸散量的时间信息熵，评价3种PM模型模拟的蒸散在时间分布上的均衡度，熵值越大表示模型模拟蒸散分布越均匀。

3 结果与分析

3.1 关键土壤水分参数确定及分析

鉴于田间持水量对PM模型分析的重要性，选用经验公式(1)(3)相互对比验证的方式来确定10个监测点的相应土壤水分参数值。图3为两种不同经验公式计算的田间持水量情况，结果表明两者相差不大，且在不同监测点的空间变化具有一致性；式(1)较式(3)计算的量值略高2%～3%，相对误差在4.76%～7.43%，表明式(1)在永年区计算θFC适用，可作为模型土壤水分参数的输入。所有监测点的田间持水量值在43.6%～24.14%，其中监测点F黏粒含量最少，θFC最低，持水性差，监测点E则与之相反，持水性好，θFC最高。所有监测点的凋萎含水量在8.78%～5.76%，与田间持水量的变化规律一致。

图3 关键土壤水分参数Fig.3 Key parameters of soil moisture

3.2 蒸散模拟结果评价

3.2.1 蒸散特性及精度评价

3种PM模型模拟及水量平衡计算的各监测点2日蒸散量变化过程如图4所示。图4可反映各监测点在关键生长期的蒸散均呈现波动中有所上涨的演变规律。大部分监测点在该过程中存在7～9轮的波动，水量平衡计算结果的趋势线斜率在1～1.5之间；相比之下，监测点D波动轮数减少且波动幅度明显更大，监测点E波动轮数增多且波动幅度偏小。各监测点出现蒸散最大峰值的日期不尽相同，大致分别在5月1日、5月17日、5月21日左右出现，总体都集中在抽穗-灌浆期，区域中部地区监测点G的峰值出现更早。整体而言，抽穗-灌浆期相较于拔节-抽穗期平均2日蒸散量均有一定程度的提升，而监测点D和H蒸散量较高，监测点F和E的蒸散量较低。

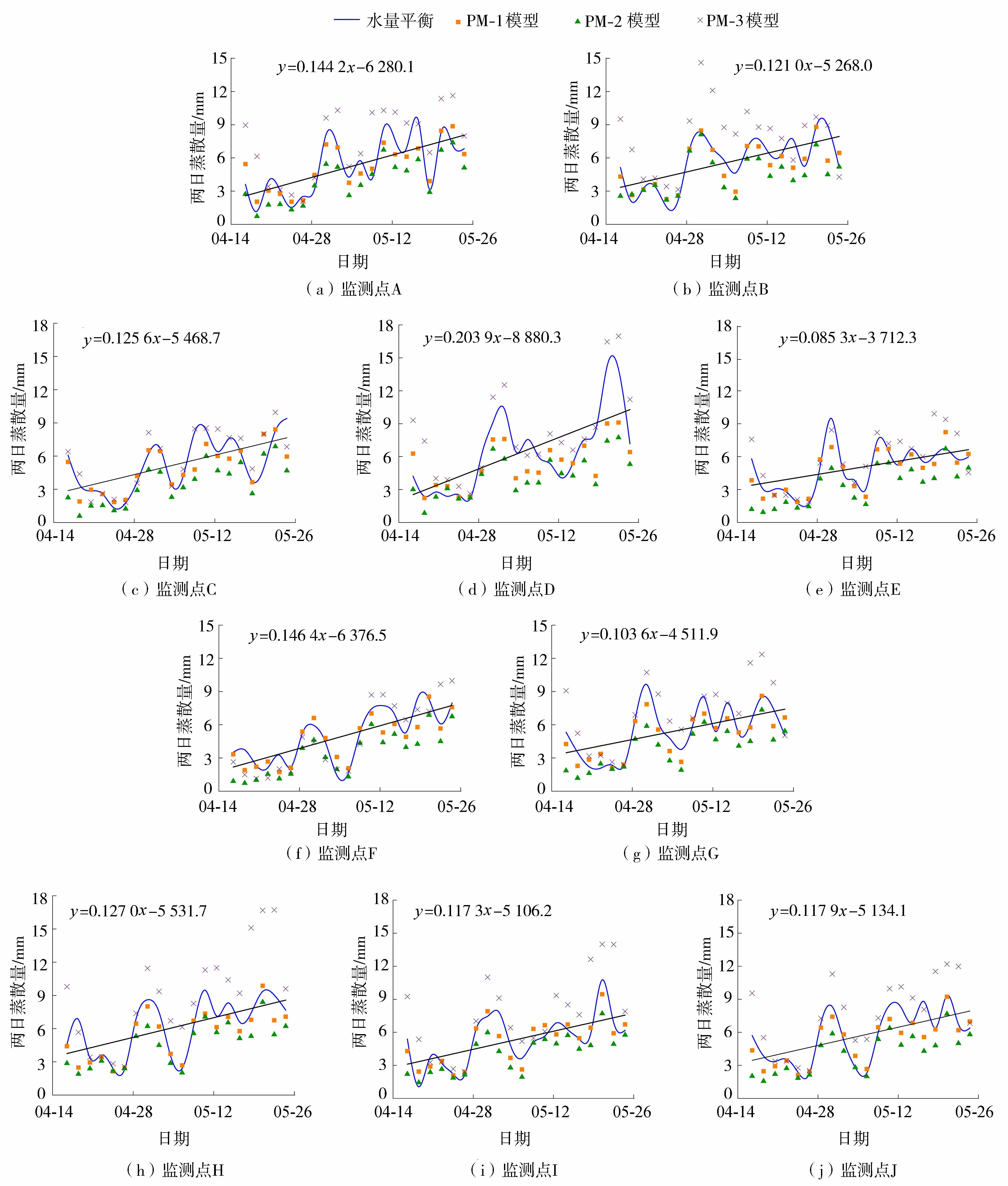
图4 各监测点蒸散模型模拟值与水量平衡计算值比较Fig.4 Comparison of simulated evapotranspiration and water balance results in various monitoring point

在不同的监测点蒸散模拟中，PM-2模型结构下蒸散模拟点相对更多地低于水量平衡蒸散曲线，而PM-3模型结构下蒸散模拟点则更多地高于水量平衡蒸散曲线，并且PM-3模型结构存在过高的蒸散估算点，表现在监测点B的拔节-抽穗期和监测点H的抽穗-灌浆期较为明显。由图4直观而言，整体PM-1模型的模拟点与水量平衡蒸散曲线更接近，相比而言，更适用于研究区。

为进一步量化体现3种模型的模拟效果，10个监测点不同模拟评价结果如表3所示。模拟结果从平均水平来看，PM-1模型的MAE、RMSE、NRMSE均是三者最小，R2、AI均是三者最大，说明PM-1模型在各指标反映层面均达到误差最小、拟合度最高、效果最优；其次是PM-2模型，除NRMSE和AI，其余指标结果均优于PM-3模型。

表3 各监测点蒸散模拟精度比较

就不同监测点的模拟效果而言，PM-1模型模拟结果的MAE、RMSE、NRMSE均在监测点D的精度最差，R2、AI分别在监测点C和G的精度最差。PM-2模型模拟结果的MAE、RMSE、NRMSE最差值与PM-1模型相同，而R2和AI表现最差的分别在监测点B和D。PM-3模型模拟结果的MAE、RMSE、NRMSE均在监测点H的精度最差；其R2和AI均在监测点B的精度最差。综上可知，不同PM模型在永年区蒸散模拟均具有较好的适应性，但整体相比而言，PM-1模型在不同评价指标的精度上均优于PM-2模型和PM-3模型。

在上述分项评价指标的基础上，采用GPI对3种模型的整体模拟精度进行排名，GPI越大，排名越靠前，模拟效果越好，结果见表3。PM-1模型模拟结果在监测点G和J中具有更优的精度表现，PM-2模型和PM-3模型的模拟结果最优的两个监测点分别为H和I、C和D。整体比较而言，PM-1模型的模拟结果在大多数监测点中的排名均最靠前，表明整体上PM-1模型较PM-2模型和PM-3模型具有精度上的优势，能够更适用于区域内多个不同典型麦田的蒸散模拟。

此外，对于PM-2模型和PM-3模型的模拟结果而言，在A、B、I、H、G和B这6个监测点中PM-2模型的排名比PM-3模型靠前，剩余4个监测点则PM-3模型的排名靠前。从总体模拟更优的数量上看，PM-2模型比PM-3模型更好，从空间分布而言，PM-2模型模拟在研究区的东部和中部麦田精度较好，而PM-3模型的较优结果更多地分布于研究区的西部麦田。

3.2.2 时间分布均衡度评价

为了对比分析3种PM模型模拟的蒸散在时间分布的均衡度，计算各麦田关键生长期2日蒸散量的时间信息熵值，如图5所示。熵越大，不确定性越强，变量分布越趋于均匀[32]。由图5可见，所有监测点中PM-1模型的信息熵值均高于PM-2模型和PM-3模型，表明PM-1模型模拟的蒸散比PM-2模型和PM-3模型模拟的蒸散在时间分布上更趋于均匀，有序度更高；在监测点B、D、F、H、I中PM-2模型的信息熵值高于PM-3模型，其余5个监测点PM-3模型高于PM-2模型。从10个监测点的信息熵平均值分析，PM-1模型、PM-2模型和PM-3模型分别为4.204 bit、4.158 bit、4.167 bit，也表明PM-1模型模拟蒸散在时间分布上具有更高的均衡度，而PM-2模型和PM-3模型在时间分布均衡度上较接近，其中PM-2模型略差。

图5 蒸散时间均衡度对比Fig.5 Temporal comparison of evapotranspiration equilibrium

3.3 讨论

本文3种模型都是对PM修正模型的修订，不同的修订参数和方式势必造成结果的差异。由式(5)可知，PM模型中等式右侧分子中的第一项Δ(Rn-G)是可用能量的量化，第二项ρCP(es-ea)/ra是空气干燥能力的描述，而分母中是通过地表阻力表示其他环境因子对蒸散的影响[33]。分母一致的情况下，分子中的可用能量项数值往往远大于空气干燥能力项数值(研究区2019年整个小麦关键期可用能量项数值约为空气干燥能力项数值的116倍)，空气干燥能力项基本处于可忽略的地位。PM-1模型正是利用该特点，抓主要项、舍次要项，采用对可用能量的分割计算Ec和Es，相比PM-2模型，模型结构更简约、计算较方便且不失准确性；PM-2模型在计算Ec和Es时分割整个地表，均考虑了对空气干燥能力的表达，相比PM-1模型，模型物理意义构成更完整；PM-3模型在分母计算上明显区别于PM-1模型和PM-2模型，固定地表阻力为70 s/m后模型阻力参数的确定易化而通用性变强，但由于最终依赖于一个综合系数对参考作物蒸散进行修订和转化，因而需要对准确获取该系数提高要求。

对于研究结果，PM-1模型相比PM-2模型的模拟精度更高，从模型本身公式表达和参数计算过程中究其原因进行探讨：①PM-2模型相比PM-1模型的Es表达更复杂并接近PM修正模型原公式，添加代入了更多的气象参数与土壤水分参数，尽管增强了模型的物理意义，但同时也加大了参数误差累积的可能性，其实际结果表明反而降低了PM-2模型的模拟精度。②PM-1模型和PM-2模型在Ec公式的表达上差别不大，在Es上的明显差别成为最终蒸散模拟结果较为不同的主要原因。在Es的计算中，PM-1模型和PM-2模型分别参考了文献[16]和[12]确定f～θ10和rs～ms之间的关系，前者基于华北平原区大量相关数据率定了该关系，而后者的研究区为美国南部大平原，显然PM-1模型与本文研究区适配度更高，保证了PM-1模型在研究区的模拟精度。

相较PM-1模型和PM-2模型，PM-3模型的蒸散模拟值整体偏高，其原因在于E0具有蒸散能力的性质，而计算的综合经验系数对其修正力度不够。具体而言：①相比PM-1模型和PM-2模型，PM-3模型缺少辐射、温度影响因子的修正考虑；②修正影响因子在公式中的置放位置至关重要。PM-1模型和PM-2模型针对rc的修正是对计算过程的修正，而PM-3模型针对E0的修正，是对计算结果的修正，前者物理成因上的关联更紧密具体，后者存在修正了整个公式中无物理联系的其余参数的可能而产生误差。

4 结 论

a.由模拟结果的精度对比分析可知，在冬小麦关键生长期，PM-1模型的农田蒸散模拟精度最高，R2和GPI的平均值分别可达0.773和3.105；其次是PM-2模型，R2和GPI的平均值分别为0.724和-1.745；PM-3模型的模拟精度最低，R2和GPI的平均值分别为0.701和-2.904。

b.从模拟结果的时间分布均衡度来说，PM-1模型的信息熵值明显高于PM-2模型和PM-3模型，具有高均衡度和有序度的特点。

c.PM-1模型、PM-2模型和PM-3模型各具优势和局限，综合分析表明，PM-1模型更适应研究区不同典型麦田关键生长期的蒸散模拟，可作为邯郸市永年区蒸散模拟和修订的工具。