电磁失电制动器机电一体化仿真技术研究
陈开楼,张稳桥,曾晓松,刘 勇
(贵州航天林泉电机有限公司,贵州 贵阳 550081)
0 引言
电磁制动器是现代生产中常见的一种自动化执行元件,具有使运动部件减速、停止或保持停止状态等功能,其操作简单、反应较快[1],国外在制动器设计方面,普遍采用计算机辅助产品设计(CAD),计算机辅助工程分析(CAE)和计算机仿真技术。近年来,虽然我国制动器设计制造技术在不断发展,但与发达国家比仍存在一定差距,在理论和工程实践方面需要开展进一步研究。因此,本文通过Ansys对电磁制动器的电磁吸力随气隙的变化规律、响应时间随气隙的变化规律、响应时间随弹簧力的变化规律等进行了仿真分析,提供一种电磁仿制动器的辅助设计方法,对电磁制动器的设计有着重要的意义。
1 电磁失电制动器结构及工作原理
1.1 电磁失电制动器结构
电磁失电制动器具有体积小、重量轻的特点,其制造工序多,涉及精密机械、精细化加工、绕组加工,其生产加工能力需求较高。结构设计是制动器设计的基础,其决定了整机方案的可行性、工艺性以及可靠性,所以整机的结构设计是关键[2-5]。制动器主要由磁轭、线圈、衔铁、弹簧、制动盘、盖板、摩擦片等零部件组成,其结构框图如图1所示,详细结构如图2。

图1 电磁失电制动器结构框图
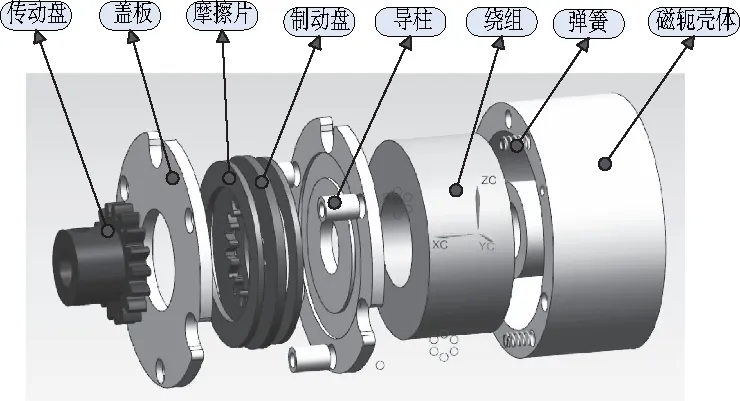
图2 电磁失电制动器三维结构爆炸图
1.2 电磁失电制动器工作原理
电磁失电制动器可实现通电快速解锁,失电迅速制动功能,其工作原理见表1。
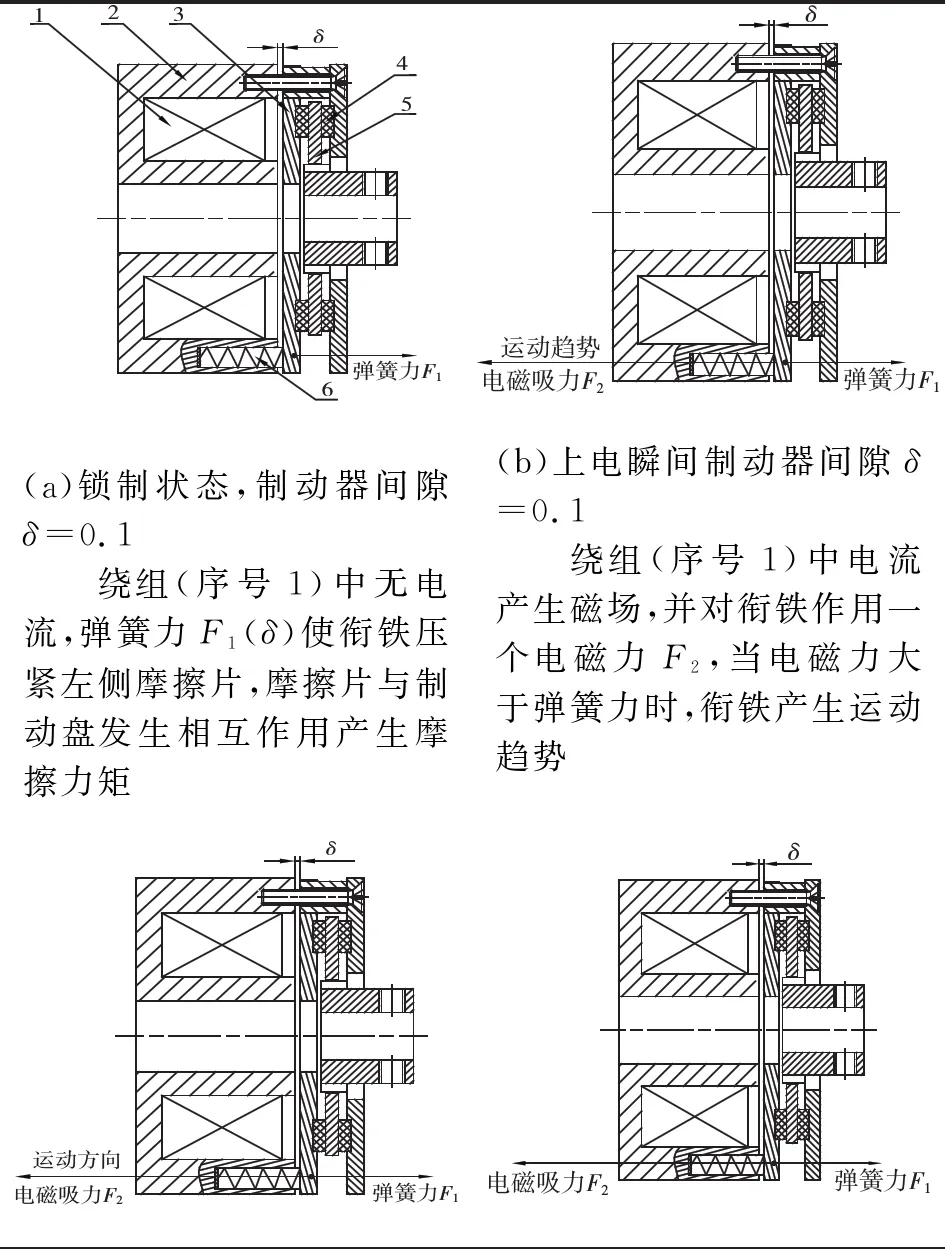
表1 制动器工作原理简述

续表1
2 电磁失电制动器机电一体化仿真技术研究
2.1 仿真模型建立
本项目拟选用常温下摩擦系数为0.42的摩擦片。根据相关公式,结合制动器体积,确定摩擦片内外径,采取适当裕量设计,以0.26 N·m为目标力矩,所需弹簧力为52 N。

图3 制动器三维仿真模型
依据上述结论及弹簧弹力,对电磁吸力进行优化设计。建立制动器磁路结构有限元模型,不断优化,平衡磁轭内外圈磁密及内外气隙磁密。优化后磁路结构模型如图3,并对制动器磁轭壳体、线圈、衔铁、求解域、运动区域进行网格剖分,其剖分效果分别如图4-图6。制动器网格划分均匀,满足瞬态场有限元分析的要求。

图4 壳体与线圈网格剖分图

图5 衔铁与运动区域网格剖分图

图6 求解域网格剖分图
制动器动态响应仿真需要增加外电路,进行场路耦合的机电一体化仿真,电路如图7。

图7 制动器动态响应仿真电路图
2.2 研究内容
电磁失电制动器机电一体化仿真内容见表2,经过机电一体化仿真,确保制动器制动力矩及响应时间等指标满足要求的前提下,进行磁路优化,提高制动器制动力矩密度,探索响应时间随气隙、弹簧弹力、温度等变量的变化规律,实现具有快响应功能的高制动力矩密度失电制动器设计。
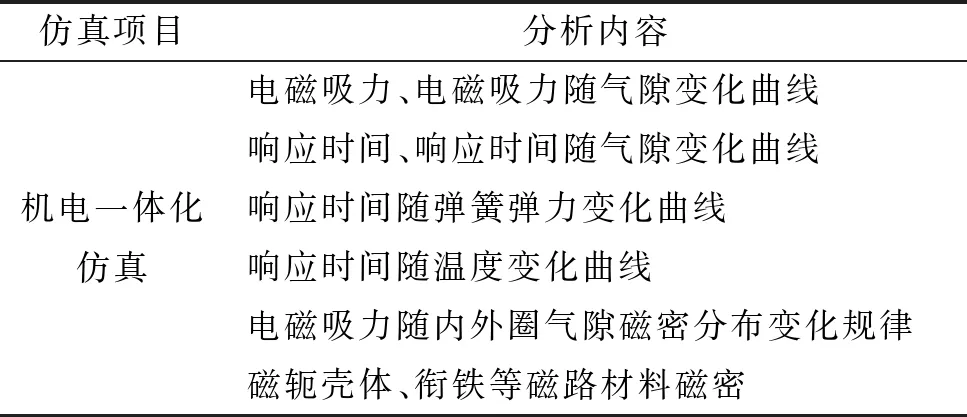
表2 机电一体化仿真分析内容
2.2.1 电磁吸力随气隙变化规律研究
仿真时设定摩擦片在运动域内沿着Z轴运动,摩擦片的行程为0.1 mm(气隙为0.1 mm),制动器解锁时,摩擦片沿着Z轴负向运动,逐渐靠近磁轭壳体端面。由前文分析可知,磁场吸力与气隙大小及内外侧平均气隙有关,对磁轭与衔铁间气隙进行了优化设计。图8为磁吸力随气隙大小的变化曲线,可知,随着气隙增大,磁吸力逐渐变小。因此,气隙越小,电磁吸力越大,可实现更高的制动力矩密度。

图8 磁吸力随气隙变化曲线
2.2.2 响应时间随气隙变化规律研究
磁路结构及材料相同的情况下,分别对气隙为0.05 mm、0.1 mm、0.15 mm、0.2 mm时制动器的解锁和制动过程的电流随时间变化曲线进行仿真,从而得出不同气隙对应的制动器响应时间。其中,图9、图10分别为气隙0.1 mm时对应的制动器解锁过程和制动过程中电流变化曲线。

图9 制动器解锁过程电流随时间变化曲线

图10 制动器锁制过程电流随时间变化曲线
从图中可以看出,制动器解锁时间为9.1 ms,满足指标要求(≤12 ms),制动时间为11.4 ms,满足指标要求(≤20 ms)。图11、图12分别为制动器解锁时间、锁制时间随气隙变化曲线,可知,在其他条件相同的情况下,制动器的解锁时间及锁制时间随气隙变大而线性变大。

图11 解锁时间随气隙变化规律
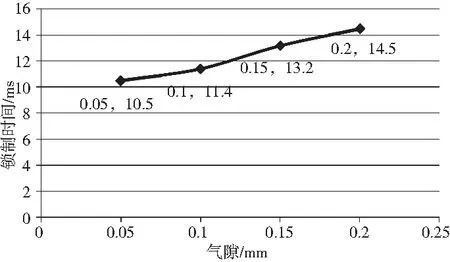
图12 锁制时间随气隙变化曲线
2.2.3 响应时间随弹力变化规律研究

图13 解锁时间随弹力变化曲线
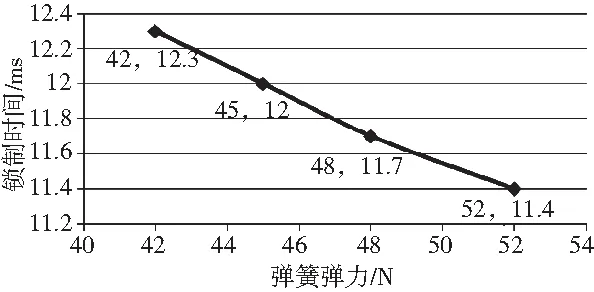
图14 锁制时间随弹力变化曲线
磁路结构及材料相同情况下,取气隙0.1 mm,分别对弹力为42 N、45 N、48 N、52 N时制动器的解锁和制动过程的电流随时间变化曲线进行仿真,从而得出不同弹力对应的制动器响应时间。分别如图13、图14所示。可见,随着弹簧弹力变大,解锁时间呈现增大趋势,锁制时间呈现减小趋势。因此,制动器设计过程中,制动力矩满足要求的前提下,尽量减小弹簧弹力,有助于提高制动器响应速度。
2.2.4 响应时间随温度变化规律研究
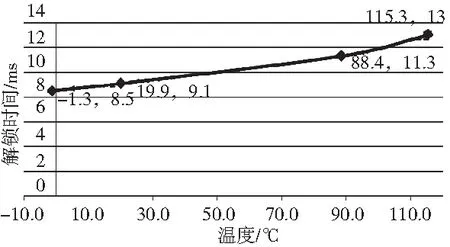
图15 解锁时间随温度变化曲线
铜电阻与温度正相关,制动器通电电压一定的情况下,电阻与电流成反比,因此改变电流值可等效实现温度的变化。磁路结构及材料相同的情况下,取气隙0.1 mm,分别对线圈电流为0.18 A、0.165 A、0.13 A、0.12 A(对应环境温度分别为+115.3 ℃、+88.4 ℃、+20 ℃、-1.3 ℃)时制动器的解锁过程的电流随时间变化曲线进行仿真,从而得出解锁时间随温度变化规律。因制动器锁制过程中制动器处于失电状态,线圈电阻的变化不会对锁制时间产生影响,而弹簧弹力几乎不受温度影响,因此温度变化仅影响制动器的解锁时间。制动器解锁时间随温度变化规律如图15所示,可知,随着温度升高,制动器解锁时间增大,因此最大环境温度对应的解锁时间符合要求,才能保证制动器全温度范围内的工作可靠性。
2.2.5 电磁吸力随磁路内外圈气隙磁密分布变化规律
制动器气隙分线圈内侧气隙和线圈外侧气隙,简称为内气隙和外气隙,文献[5]中通过解析法理论推导,证明只有当内气隙平均磁密与外气隙平均磁密相等时,制动器磁路结构才为最优,具有最大的电磁吸力。此处使用仿真软件,对该结论形成仿真结果支撑。
经不断调整制动器磁路结构,发现内外气隙平均磁密差值越小,电磁吸力越大,当内外气隙平均磁密值相等时,电磁吸力最大。图16、图17分别为内、外气隙平均磁密相等时的磁密分布图。

图16 内侧气隙磁密分布
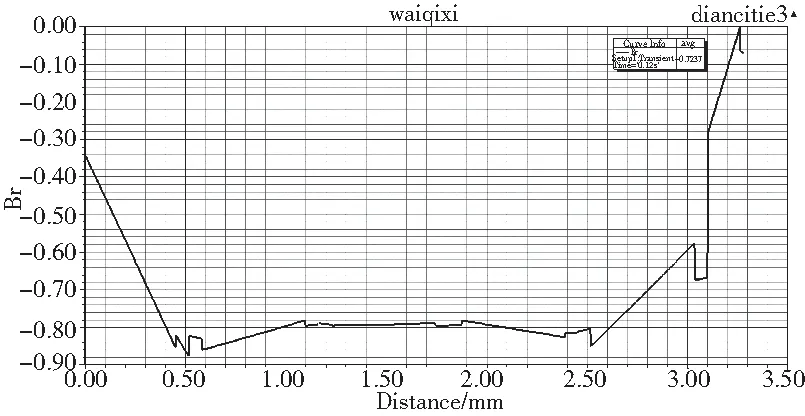
图17 外侧气隙磁密分布
2.2.6 磁轭壳体、衔铁等磁路材料磁密仿真

图18 磁力线分布图
磁轭壳体、衔铁共同组成制动器的磁路,机电一体化仿真过程中,当电磁吸力满足要求时,受磁路材料饱和磁密限制,必须对磁路材料磁密进行仿真。项目制动器磁路磁密分布如图18、图19,可以看出,制动器磁路部分最高磁密仅1.6T,而拟选用高导磁材料饱和磁密大于1.8T,因此磁密无局部饱和问题,制动器可以可靠工作。

图19 衔铁和磁轭磁密分布图
3 仿真结果
通过上述仿真,及综合考虑结构、电磁、力、热等因素对制动器响应速度及制动力矩的影响,最终选择参数如下:额定电压24 V,额定功率4 W,解锁电压小于等于18 V,静态制动力矩0.26 N·m,气隙长度0.1 mm,解锁时间小于等于20 ms,锁制时间小于等于12 ms。
4 测试结果
对其测试,结果如下,制动器工作电流和解锁电压测试接线如图20所示。测试工作电流为0.162~0.168 A,解锁电压为10.3~13.7 V,额定电压为24 V,计算制动器功率等于额定电压乘以工作电流得3.98~4.03 W,测试解锁时间与锁制时间接线如图21,解锁时间波形如图22,当电流从零上升到第一个峰值时,为衔铁开始运动的点,此时制动器成解锁状态,电流下降到第一个峰值时,此时衔铁到达解锁最终位置,最后电流持续上升逐渐到达稳定工作电流,测试得到电流从零上升到第一个峰值的时间为11.5~15.6 ms,即解锁时间为11.5~15.6 ms;锁制时间波形如图23,当电流从最大值下降到最低点然后上升到第一峰值时,制动器完成锁制,测试得到时间为10.3~13.6 ms,即锁制时间为10.3~13.6 ms。实测试数据如表4。

图20 工作电流和解锁电压测试接线图 图21 解锁时间与锁制时间接线图

图22 解锁时间波形图 图23 锁制时间波形图

表3 仿真与实测对比数据
5 结论
针对电磁失电制动器各指标的机电一体化研究,综合考虑结构、电磁、力、热等因素对制动器响应速度及制动力矩的影响,量化研究电磁吸力随气隙变化规律及响应时间随气隙变化规律、磁吸力最大时锁制时间随弹簧弹力变化规律、解锁时间随温度变化规律等,并通过多目标寻优方式,平衡电气性能与机械性能之间的相互影响与制约,最终对磁路材料磁密进行校核,保证制动器能可靠实现高制动力矩密度,可实现快响应、高制动力矩密度的电磁失电制动器设计。实测结果与仿真结果基本一致,因此,本文所述机电一体化仿真方法对失电制动器精准仿真设计具有重要意义。

