柱式弹性体的端面载荷分布和结构尺寸对端部效应的影响规律
韦铁平,林守强,杨晓翔,郭金泉,花海燕,林硕
(1.福建工程学院机械与汽车工程学院,福建 福州 350118;2.福建省计量科学研究院,福建省力值计量测试重点实验室,福建 福州 350003;3.福州大学机械工程及自动化学院,福建 福州 350108)
0 引言
柱式负荷传感器端面上变化的载荷分布将引起传感器示值发生改变的现象,称为端部效应[1].作为传感器测量误差的一个重要影响因素,端部效应的研究受到广泛关注[2-3].为研究端部效应的影响因素,对传感器压头的接触表面形状和硬度两个重要因素进行试验分析.Debnamr等[4]的结果发现,压头接触表面的形状对端部效应的影响远大于压头硬度对端部效应的影响.这说明,端面的载荷分布对端部效应影响很大.为寻求端部效应最佳的柱式弹性体尺寸,Robinson[5-6]对变化长径比的柱式弹性体进行模拟分析,发现长径比为3.5的柱式弹性体端部效应为零,并在此基础上,通过弹性力学理论及试验验证,发现长径比在1.3~1.7范围内存在另外一个端部效应零点,且载荷分布形式对端部效应影响很大.基于弹性力学理论,对称的两端面载荷分布作用下的解析解通过引入两个解耦位移函数获得[7].
此外,传感器端面与压头之间的摩擦特性对端部效应也有影响.研究发现,力值传递过程二者之间存在剪切应力,这将引起输出示值的滞后及端部效应[8-9].压缩试验下,由于端面与试验机接触面之间的接触摩擦特性,柱式弹性体的应变将发生非均匀性变化[10-11].综上所述,柱式负荷传感器的端部效应不仅受到载荷大小和分布形式的影响,同时还取决于其结构尺寸.而现有文献极少有涉及结构尺寸应对端部效应影响的研究.
因此,本文取长径比1.0的柱式弹性体为研究对象,不考虑弹性体端面与压头间的摩擦特性,针对端面的载荷分布和结构尺寸对端部效应的影响进行研究.首先,对两种情况建立力学边界条件模型,并以载荷分布模型为例推导其平衡微分方程;其次,引入两个解耦位移函数来表达解析解;最后,根据边界条件计算待定系数,并确定各应力分量值.进一步地,结合胡克定律讨论两种边界条件下传感器桥路输出随着贴片位置的变化规律.
1 理论分析
1.1 边界条件
如图1所示,选择柱式负荷传感器关键受力部件—柱式弹性体作为研究对象,考虑到尺寸大小和理论分析需求,将柱式弹性体简化为直圆柱体[12].假设所分析的有限长圆柱体为均匀各向同性的线弹性体,半径为R,长度为2H,如图2所示.模型的柱坐标系(r,θ,z)原点O和Z轴分别为柱体的中心和对称轴.
首先,研究弹性体非对称、非均匀性载荷分布对端部效应的影响规律,弹性体两端面的载荷分布如图2(a)所示.图2(a)中显示,右端面受到均匀分布的拉伸载荷与环状形分布的压缩载荷作用,环状形载荷分布平均半径为x0,宽度为δ,且右端面上的合力为零.此外,左端面上无载荷作用,可看作均匀性载荷分布.其次,研究尺寸效应对端部效应的影响,两端面的载荷分布情况如图2(b)所示.弹性体右端面受到均匀分布的拉伸载荷与圆面分布的压缩载荷叠加作用,圆面半径为r0.此外,右端面合力为零,左端面上无载荷作用,可看作均匀性载荷分布.

图1 柱式负荷传感器结构示意图Fig.1 Structural diagram of column load sensor

图2 基于弹性力学理论分析的柱式弹性体力学模型Fig.2 Mechanical models of the cylindrical elastomer based on the theory of elasticity
由图2可知,由于右端面上载荷分布不同,两个力学模型右端面的轴向应力σz(r)分布存在差异,其他应力分量一致.二者边界条件如下:
在柱体侧表面r=R上,
σ=0,τrθ=0,τrz=0
(1)
在柱体两端面z=±H上,
τzr=0,τzθ=0
(2)
在左端面z=-H上,
σz=0
(3)
在右端面z=+H上,σz(r)在载荷分布条件和尺寸效应模型下分别为:
(4)
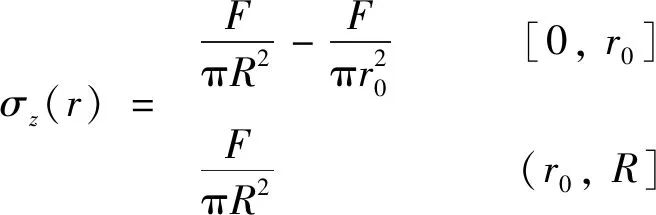
(5)
其中:作用于右端面上的拉伸载荷和压缩载荷的合力均为F.
两个力学模型的解析解推导过程相似,下文以载荷分布模型为例进行推导.
1.2 平衡微分方程
根据胡克定律,本构方程为:
σij=2Gεij+λεkkδij
(6)
其中:i、j、k=r、θ、z,λ为Lame常数,λ=2μG/(1-2μ),G为剪切弹性模量;δij为Kronecker函数(当i=j时,δij=1;当i≠j,δij=0);σ和ε分别为应力张量和应变张量,应变与位移关系可表示为:

(7)
其中:u=urer+uθeθ+uzez;∇u为位移梯度张量;式(7)中应变张量分量为:

(8)
不考虑体力,将式(8)代入式(6)可得位移函数表示的应力,然后代入∇·σ=0,则平衡微分方程为:

(9)
其中:Ω=[(∇u)T-∇u]/2,为自旋张量;e=∇·u,为体积应变.
2 位移函数求解
2.1 位移函数
对于有限长圆柱体轴对称解析解的求解,Love[13]通过引入单个位移函数推导;胡海昌[14]引入两个位移函数来表示空间问题的通解;侯宇等[15]采用H变换和Stocks变换推导;Chau等[16]提出采用双Fourier级数表示的双位移函数求解解析解.本研究则根据文献[16]引入两个位移函数Φ和Ψ.

(10)
其中,

(11)
将式(10)代入式(9),可得解耦控制方程

(12)

联立式(6)、(8)和(10),应力分量为:

(13)

(14)

(15)

(16)

(17)

(18)
2.2 位移函数的级数表达式
根据文献[14],有限长圆柱体在任意端面载荷作用下的两个位移势函数的级数表达式为:

(19)

(20)

由图2可知,力学模型为轴对称问题,因此所有的应力变量和位移变量均与θ无关.故ωn=0,Ψ=0,τzθ=τrθ=0及l=0,式(20)简化为:

(21)
其中:k=1,2;J0和I0分别为零阶Bessel函数和零阶修正的Bessel函数;λs为J1(x)=0的正零根.当k=1时,关于z的函数为奇函数sin(ηmz)、sinh(γsz)和zcosh(γsz);当k=2时,关于z的函数为偶函数cos(ηmz)、cosh(γsz)和zsinh(γsz).
3 待定系数的确定
将式(21)代入式(13~18),并做推导.将式(13)和式(15)关于z进行Fourier-Bessel级数展开,结合边界条件(1)有
(2μ-1)C0+μA0=0
(22)

(23)

(24)
根据边界条件(1)及式(16),有

(25)

(26)
将式(14)和式(15)关于r进行Fourier-Bessel级数展开,结合边界条件(2)有

(27)

(28)
将σz(r)进行Fourier-Bessel级数展开,并结合上式与边界条件(4)有
2(2-μ)C0+(1-μ)A0=0
(29)
其中:Gs(r0)为σz(r)进行Fourier-Bessel级数展开的系数,根据文献[13],Gs(r0)为:

(32)

4 数值模拟结果与讨论
4.1 无量纲化计算的参数设置

图3 桥路输出计算流程图Fig.3 Flow chart of bridge output calculation
为使研究具有普遍性,对物理量单位归一化.各物理量数值设置如下:拉伸载荷和压缩载荷F=π;弹性模量E=1.0;尺寸R=H=1.0;材料的泊松比μ=0.3.为分析轴对称非均匀性载荷的影响,图2(a)中右端面上δ足够小(ε0=10-4,ε0为环状形面积与弹性体横截面的比值)时,认为环状形压缩载荷为集中力;为研究结构尺寸对端部效应的影响,图2(b)选择r0/R=0.5.根据桥路输出公式,其输出值正比于(εz-εθ),记作εb;εb值越大表示端部效应越明显,计算流程图见图3.
4.2 结果与讨论4.2.1 端面载荷分布对端部效应的影响
图4为在变化的轴对称非均匀性载荷下,弹性体引起周向应变、轴向应变和桥路输出的变化曲线图.载荷分布如图4(a)时,压缩载荷沿径向平均半径取x0=0、0.2、0.4、0.6、0.8和1.0.
从图4(a)可知,周向应变在变化载荷分布下,其曲线变化十分复杂.周向应变值在z≈0.6H和z≈-0.5H处发生变号,且x0=0、0.2、0.4和0.6时的周向应变变化趋势与平均半径为x0=0.8和1.0时相反;此外,x0=0、0.2、0.4和0.6的周向应变比x0=0.8和1.0的波动幅度剧烈,且最大值发生在两端面附近.
从图4(b)可知,除两端面附近,平均半径x0=0、0.2、0.4和0.6载荷分布作用下的轴向应变呈单调递增,且均为正值;x0=0.8和1.0时,轴向应变呈单调递减,且均为负值.在两端面附近的轴向应变变化剧烈,尤其是受到非均匀性载荷分布的一端;但当远离端面时,轴向应变变化平缓,符合圣维南原理.
由图4(a)和图4(b)可知,轴向应变比周向应变大得多.因此,桥路输出变化曲线与轴向应变十分接近,如图4(c)所示.桥路输出在两端面变化最剧烈,尤其是在轴对称非均匀性载荷分布的右端面.此外,桥路输出零点出现在z≈-0.625H,即远离加载端面约为1.625H处,该值与文献[17]一致,说明了本文计算的准确性.

图4 端面不同载荷分布下的变化曲线图Fig.4 Changing curves under different loading distribution
4.2.2 端部效应的灵敏度

图5 端部效应灵敏度κ随着长径比d0的变化规律Fig.5 Sensitivity of end effect κ versus aspect radio d0

4.2.3 结构尺寸对端部效应的影响


图6 结构尺寸对端部效应的影响规律曲线Fig.6 Influence curves of structure size on end effect
由图6(a)可知,周向应变端部效应曲线呈抛物线形状.由于载荷分布的非对称性,抛物线对称轴偏向右端;周向应变最大值发生在两端面处;且随着尺寸的增大,周向应变的端部效应减小.由图6(b)和图6(c)可知,轴向应变的端部效应远大于周向应变的,因此桥路输出的端部效应与轴向应变的分布几乎一致.由图6(c)可知,桥路输出值的端部效应为单调递增(除了右端面附近的一小段),零点在z≈-0.55H处,即远离加载端面约为1.55H处,落在(1.30~1.70)H范围内,与文献[17]一致;且在非均匀性载荷作用下,右端面的端部效应远大于左端的.

图7 结构尺寸对端部效应的影响规律Fig.7 End effect versusstructure size for the cylinder
为深入研究尺寸对端部效应的影响,考察长径比为1.0圆柱体的端部效应随着结构尺寸的变化规律.以尺寸R=H=0.5作为基数,则尺寸增长倍数依次为1.0、1.5、2.0、2.5、3.0、3.5和4.0倍.以桥路输出的端部效应最大正值来计算端部效应随着尺寸倍数增大的衰减速度关系,如图7所示.图中显示,结构尺寸对端部效应的影响十分显著.随着尺寸的增大,端部效应呈非线性衰减,端部效应的衰减值与尺寸增长倍数对应的值分别为100%、44.5%、25.1%、16.1%、11.1%、0.08%和0.06%.由此可知,尺寸越小,端部效应对结构尺寸越敏感;随着尺寸增长倍数的增加,敏感度迅速衰减.因此,弹性体的设计尺寸要合理,尺寸过小,将带来较大的端部效应;尺寸过大,抑制端部效应效果不明显且不利于传感器结构轻巧化的要求.
5 结语
1) 两个力学模型的端部效应分布规律符合圣维南原理,且零点落在(1.3~1.7)H区间内,说明模型计算结果的准确性.
2) 柱体两端面非对称的载荷引起的端部效应也为非对称的,且端部效应在非均匀载荷分布的一端比均匀分布的一端变化更加剧烈;柱式弹性体长径比越大,端部效应受到端面载荷分布的影响越小.
3) 大尺寸柱式弹性体有利于抑制端部效应,但当弹性体尺寸增大超过3.5倍时,通过增大尺寸来抑制端部效应的效果迅速消失.

