基于邻域驱动的粒子群算法
李国森,闫 李,郭倩倩,赵启凤,岳彩通
(1.中原工学院 电子信息学院,河南 郑州 450007;2.郑州大学 电气工程学院,河南 郑州 450001;3.郑州大学 产业技术研究院,河南 郑州 450001)
0 引 言
在实际科学和工程应用中,大多数优化问题包含多个彼此冲突的目标[1]。在进行优化时,需要找到使所有目标达到最优的一组Pareto最优解集(Pareto set,PS)。所有Pareto最优解映射至目标空间形成Pareto前沿(Pareto front,PF)。基于Pareto支配关系的多目标算法是解决多目标问题的经典方法,能在一次运行后得到逼近真实PF的解集[2,3]。
在多目标优化问题中,存在一种特殊的优化问题,即多模态多目标优化问题(multimodal multi-objective optimization problems,MMOPs)[4,5]。MMOPs在决策空间中包含多个PS对应于目标空间中同一PF。研究者关注的是Pareto最优解在决策空间中的分布情况,旨在在决策空间中找到更多的Pareto最优解[6]。
为求解多模态多目标问题,Li等[7]采用多种变异策略,动态调整种群的进化方向。Tanabe等[8]引入分解的思想,划分多个子问题进行同时优化。Liu等[9]采用双档案重组策略提高决策空间的多样性。Qu等[4]采用自组织机制提高种群的寻优速度。Yue等[10]提出多模态多目标遗传算法,提高对决策空间的搜索能力。
上述研究在一定程度上提高了解在决策空间的分布性,但仍存在算法多样性缺失、获得的PS不完整等不足。本文提出基于邻域驱动的粒子群算法。算法采用邻域驱动策略,构建多个独立的邻域,引导种群开采多个解。同时采用吸收机制,借鉴邻域粒子的搜索经验,提高算法对邻域空间的深度搜索能力。
1 基本概念
1.1 多模态多目标优化问题
图1给出了多模态多目标问题示意图[11,12]。在决策空间中存在两个PS,分别为PS1和PS2。两个PS均对应于目标空间中的PF。其中,位于PS1上的A1和位于PS2上的A2均对应于PF上的A′。在决策空间中找出多个最优方案(如A1和A2),可为决策者提供多种选择。

图1 多模态多目标优化问题
1.2 粒子群算法描述
在D维决策空间中,种群POP由N个粒子组成。其中第i个粒子的位置记为xi,飞行速度记为vi,该粒子通过跟踪个体最优pbest和全局最优nbest更新自己的位置和速度[13,14]。在第t次迭代,其更新公式如下
vi(t+1)=w·vi(t)+c1·rand·(pbesti(t)-xi(t))+
c2·rand·(nbesti(t)-xi(t))
(1)
xi(t+1)=vi(t+1)+xi(t)
(2)
其中,c1、c2是学习因子,w是惯性权重;rand∈[0,1]。
2 算法设计
2.1 邻域驱动策略
标准粒子群算法在迭代后期存在种群多样性丢失,早熟收敛等问题,很难在决策空间找到多个最优解[15]。鉴于此,本文提出邻域驱动策略。基本思想是根据相似度将整个种群划分为多个邻域,每个邻域内的粒子共享最优信息,粒子独立在自己的邻域空间内独立进化,推动整个种群获得更多的最优解。具体方法为:
首先,计算粒子间距离。分别计算每个粒子与种群中其它粒子的距离。第i个粒子与第j个粒子的欧式距离定义如下
(3)
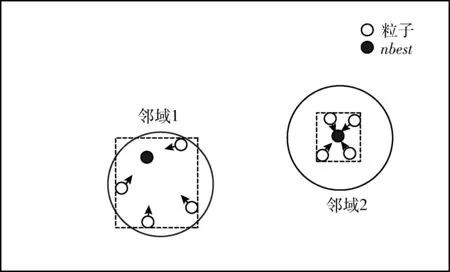
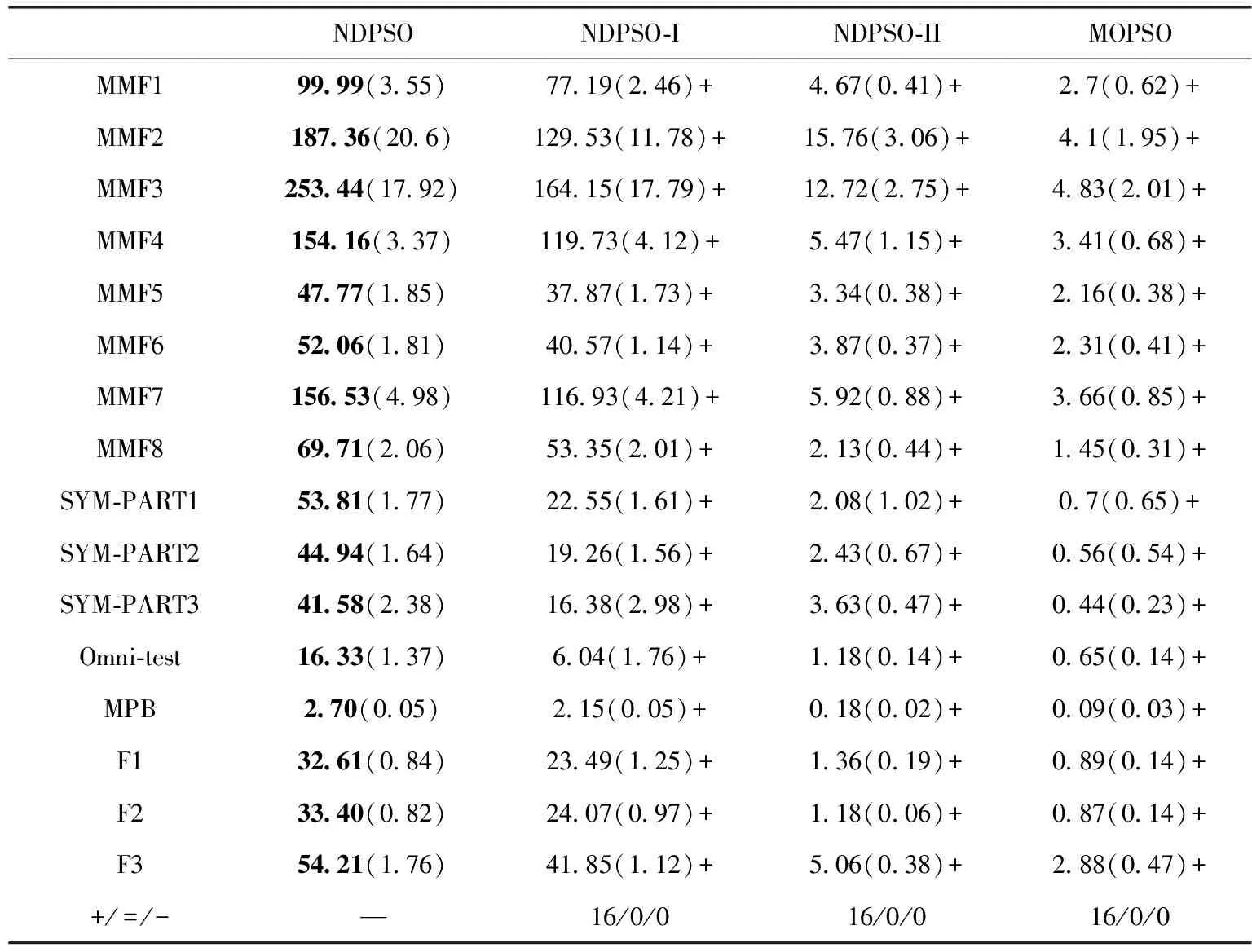
其次,划分邻域。在种群规模为N的种群POP中,集合SP表示已加入邻域的粒子,集合NLi表示第i个粒子的邻域集合,nsize表示邻域的大小。从种群POP中,先找出距离第1个粒子最近的nsize个粒子,将其加入SP和NL1中。接着找出距离第k(1 最后,分配最优nbest。第i个粒子的nbest选取方法为:对NLi中的粒子进行非支配排序,选取排在第一的粒子作为nbest。 图2给出邻域驱动策略示意图。从图2中可知,整个种群划分成4个邻域,每个邻域内包含5个粒子,其中一个粒子是邻域nbest,nbest指导邻域内个体进化。根据欧式距离作为粒子间的相似度,相似的个体被划分到同一邻域内,邻域中的个体在各自的空间内搜索。另外,邻域随着迭代次数动态更新,若某些粒子早熟停滞,在邻域信息的牵引下跳出局部区域。按照这种方式,提高粒子在寻优时的活性,种群逐渐在决策空间能够找到更多解。 图2 邻域驱动策略 在粒子群算法中,如果粒子仅被最优解引导,将快速收敛到最优解附近[16]。为了挖掘邻域内的潜在解,提高算法的搜索活力,本文提出吸收机制。基本思想是吸收邻域内所有粒子的搜索经验,引导粒子在邻域内充分开采。 假设第i个粒子的邻域集合记为NLi,该邻域的上边界记为UBi,下边界记为LBi,对角线距离记为Li。集合L记录每个粒子对应的对角线距离。 首先,在d维,上边界UBid和下边界LBid计算如下 UBid=max(NLid) (4) LBid=min(NLid) (5) 其中,NLid表示邻域集合NLi中所有粒子的第d维。 其次,依据邻域的上下边界,计算对角线距离Li。公式如下 (6) 最后,如果满足rand (7) 图3示例了吸收机制。邻域1和邻域2的搜索范围用虚线给出。相比于邻域2,邻域1的搜索范围较大。可以采用式(7)对邻域内的粒子进行更新。一方面,式(7)对邻域内所有粒子的信息进行了综合学习,促进邻域中优秀信息的流动,增强种群对邻域的搜索能力;另一方面,莱维分布兼顾小范围的开采和大范围的勘探[17,18],能够更全面搜索整个邻域,避免陷入局部区域。 图3 吸收机制 步骤1 随机初始化粒子种群POP,外部档案EXA=POP。 步骤2 根据邻域驱动策略划分邻域,为每个粒子分配nbest。 步骤3 按照式(1)、式(2)更新粒子的位置和速度。 步骤4 按照式(4)、式(5)、式(6)计算每个邻域的上下边界和对角线距离。 步骤5 判断是否采用式(7)更新粒子位置。 步骤6 更新外部档案EXA=[POP;EXA]。 步骤7 重复步骤2~步骤6,直至满足终止条件。 步骤8 输出外部档案EXA。 为了检验算法的有效性,采用12个典型多模态多目标测试函数和1个多模态多目标实际问题[4,11],分别为MMF1-MMF8、SYM-PART1、SYM-PART2、SYM-PART3、Omni-test、MPB。另外,为了进一步评估算法的性能,根据测试函数的设计方法[11],设计3个具有不同难度的测试函数,其PS和PF分布情况如图4所示。测试函数F1的表达式如下 (8) 该函数在决策空间的维度是2。决策变量x1和x2的取值范围分别为-4≤x1≤4, -4≤x2≤4。在决策空间中存在4个不连续的PS。比具有连续PS的函数更难求解。同时,在目标空间中PF存在拐点(Knee point),需要算法具有较高的收敛性。其PS和PF分布情况如图4(a)、图4(b)所示。 测试函数F2的表达式如下 (9) 该函数和测试函数F1在决策空间的维度、决策变量的取值范围、PS个数均相同。在决策空间中PS分成15个片段,比函数F1多2个,因此增加了算法的寻优难度。其PS和PF分布情况如图4(c)、图4(d)所示。 测试函数F3的表达式如下 (10) 该函数在决策空间的维度是3。决策变量x1、x2、x3的取值范围分别为-1≤x1≤1, 0≤x2≤1, 0≤x3≤1。 在决策空间中存在8个PS。其PS和PF分布情况如图4(e)、图4(f)所示。该函数的变量维度和PS个数均增加,更具有挑战性。 图4 测试函数F1、F2、F3的PS和PF 本文采用8个对比算法,分别为DE_RLRF[7]、RVEA-ADA[8]、TriMOEATA&R[9]、SSMOPSO[4]、MO_Ring_PSO_SCD[11]、MMOGA[10]、DN-NSGAII[7]、Omni-optimizer[19]。 对比算法参数保持与相应文献一致的设置。所提算法参数设置如下:c1=c2=2.05,w=0.7298,nsize=5。所有算法种群规模N=800,最大迭代次数T=100,独立运行30次[11]。此外,采用Wilcoxon秩和检验来判断算法得到的结果是否具有显著性差异。符号“+、=、-”分别表示所提算法显著优于、相似于、差于对比算法。 本文选取两个性能指标对算法进行评价: (1)帕累托解集近似性(PSP)[11]:衡量算法获得的PS的多样性和收敛性。PSP值越大,表明算法在决策空间中的性能越好。 (2)超体积(HV)[20,21]:评估算法获得的PF的收敛性和多样性。HV值越大,表明算法在目标空间中的性能越好。 3.4.1 策略性能对比 为了验证所提策略的有效性,将所提算法与MOPSO(基本粒子群算法)[11]、NDPSO-I(仅采用邻域驱动策略的MOPSO)和NDPSO-II(仅采用吸引机制的MOPSO)进行对比。表1显示了不同策略下算法的平均值和标准差。 表1 各策略PSP性能结果对比 从表1可以看出,NDPSO-I和NDPSO-II的性能明显优于MOPSO。原因是邻域驱动策略通过构造多个不同的小生境,形成相对独立的邻域空间,引导粒子在邻域内独立进化,实现对多个最优解的同步搜索。吸收机制通过对邻域信息的提取和利用,指导粒子向整个邻域搜索,促进粒子对邻域的深度开采,维持种群的进化动力。其次,NDPSO在所有测试函数上获得较好的PSP值。从秩和检验上看,NDPSO的性能在统计意义上优于对比的算法。进一步表明所提策略的有机结合,协同地提高了粒子群算法的整体性能。 3.4.2 算法性能对比 本节从两个角度对算法的性能进行比较。首先比较算法在决策空间中的性能。表2列出了不同算法在测试函数上的PSP值。如表2所示,NDPSO在所有测试函数上具有很高的PSP值,在决策空间中显示出很好的性能。SSMOPSO的性能排第二。SSMOPSO根据物种形成原理,建立多个小生境,保持种群多样性。MO_Ring_PSO_SCD的表现紧随其后。MO_Ring_PSO_SCD采用环形拓扑结构和特殊拥挤距离,增强种群的开采能力。DE_RLRF在大多数测试函数上表现较好。DE_RLRF根据种群进化状态,分配有效寻优策略,加快找到最优解的速度。Omni-optimizer和DN-NSGAII的性能接近,通过引入决策空间拥挤距离,提高解的分布性。TriMOEATA&R、RVEA-ADA、MMOGA的表现略差。TriMOEATA&R引入双档案重组机制,对维持解的多样性起到促进作用。RVEA-ADA引导种群优化多个子问题,改善种群对最优区域的探索能力。MMOGA采用邻域划分策略,有利于找到更多的解。其次比较算法在目标空间中的性能。表3给出了不同算法在测试函数上的HV值。所提算法在MMF5函数上获得了最优的HV值。RVEA-ADA在MPB上显示较好的性能。TriMOEATA&R在SYM-PART1和F3上表现很好。MMOGA在2个测试函数上获得了最高的HV值。DN-NSGAII在8个测试函数上获得了最优的HV值。Omni-optimizer在F1和F2上性能较好。其实,所有算法在相同测试函数上获得的HV值处于相同的数量级上,且接近于最优值。表明所有算法在目标空间中的表现相当。 表2 不同算法PSP性能结果对比 表3 不同算法HV性能结果对比 为了直观地比较算法的性能,图5和图6分别给出了算法在F3上获得的PS和PF。F3在三维决策空间中包含8个PS。从图5可以看出,NDPSO能够找到全部PS,且获得的PS能够均匀分布在真实PS上。DE_RLRF、TriMOEATA&R、SSMOPSO、MO_Ring_PSO_SCD找到的PS不完整,不能很好地使粒子布满整个真实PS。RVEA-ADA、MMOGA、DN-NSGAII、Omni-optimizer获得的PS分布性较差,基本上集中在PS的某一部分上。从图6可以看出,所有算法在目标空间中获得的PF相差不大,且均能覆盖到整个真实PF上。总体来说,所提NDPSO算法在决策空间中能够获得分布性良好的解集。 图5 不同算法所获得的PS对比 图6 不同算法所获得的PF对比 3.4.3 算法收敛性比较 算法的收敛性是衡量算法性能的指标之一。选取F1来测试算法收敛性。F1在决策空间具有4个PS,每个PS是不连续的,优化难度较大。将决策空间划分为4个面积相等的子区域,分别为区域1 {x1∈[-4,0],x2∈[0,4]}、 区域2 {x1∈(0,4],x2∈[0, 4]}、 区域3 {x1∈[-4,0],x2∈(-4,0]} 和区域4 {x1∈(0,4],x2∈[-4,0)}。 每个子区域均包含一个PS。收敛性是指在每次迭代时种群分布在每个子区域中解的比例[11]。如果种群在每个子区域中解的比例均等于25%,表明算法具有良好的收敛性。 图7为算法在每次迭代时的收敛性变化曲线。对于图7(a),随着迭代次数越来越大,种群在每个区域中所的比例逐渐接近25%。在第50次迭代后,种群在每个区域中比例逐渐趋于平稳,最终稳定在25%。表明所提算法在收敛性能上表现良好。对于图7(b)、图7(f),在第30次迭代后,区域1和区域3中解的比例大于区域2和区域4。表明DE_RLRF和MO_Ring_PSO_SCD在后期迭代中更侧重于优化区域1和区域3。对于图7(c),在第80次迭代之后,区域3中解的比例略大于25%,而区域2中解的比例略小于25%。表明RVEA-ADA在后期优化中,更多的粒子在区域3中搜索最优解。对于图7(d)、图7(e)、图7(h)、图7(i),每个区域的收敛曲线波动频繁,且不稳定于25%。表明TriMOEATA&R、SSMOPSO、DN-NSGAII和Omni-optimizer的收敛性能较差。对于图7(g),在第40次迭代后,区域1和区域2中解的比例明显大于区域3和区域4中解的比例。表明在迭代后期MMOGA更倾向于对区域1和区域2的探索。 图7 不同算法的收敛性对比 基于以上分析,可得出所提算法的收敛性能优于其它比较算法。 3.4.4 实际应用 为了测试算法在工程问题上的求解能力,选择一个经典的实际优化问题-基于地图的优化问题(缩写为MPB)进行实验[4]。该问题在决策空间有3个不连续的PSs。将所提算法与其它8个算法进行对比。从表1的结果可以看出,所提算法在该问题上获得PSP值高于其它对比算法。图8给出了算法的获得的PS情况。由图8可见,所提算法在决策空间具有很好的多样性,能够获得更多最优解。其它算法能够找到一部分的解,但存在获得的PS不完整。例如,MO_Ring_PSO_SCD能够找到3个PS,但得到的最优解集在部分区域有缺失。MMOGA获得的大多数最优解分布在真实PS的边界处。综上所述,所提算法在解决实际问题上是有效的。 图8 不同算法在实际应用上获得的PS对比 本文提出基于邻域驱动的粒子群算法(NDPSO)。采用了邻域驱动策略和吸收机制。邻域驱动策略将整个种群划分为多个不同的邻域,粒子在自己的邻域独立进化,增强解在决策空间的分布。吸收策略通过学习邻域潜在的有用信息,加强对邻域最优解的开采能力,增大找到更高质量解的概率。同时为了全面评估算法性能,本文设计3个多模态多目标测试函数。通过和8个多模态多目标算法相比,表明NDPSO能够提高解在决策空间的多样性,且获得的PS分布均匀。在未来的工作中,将MMOPs扩展到约束优化问题中,设计约束多模态多目标测试函数。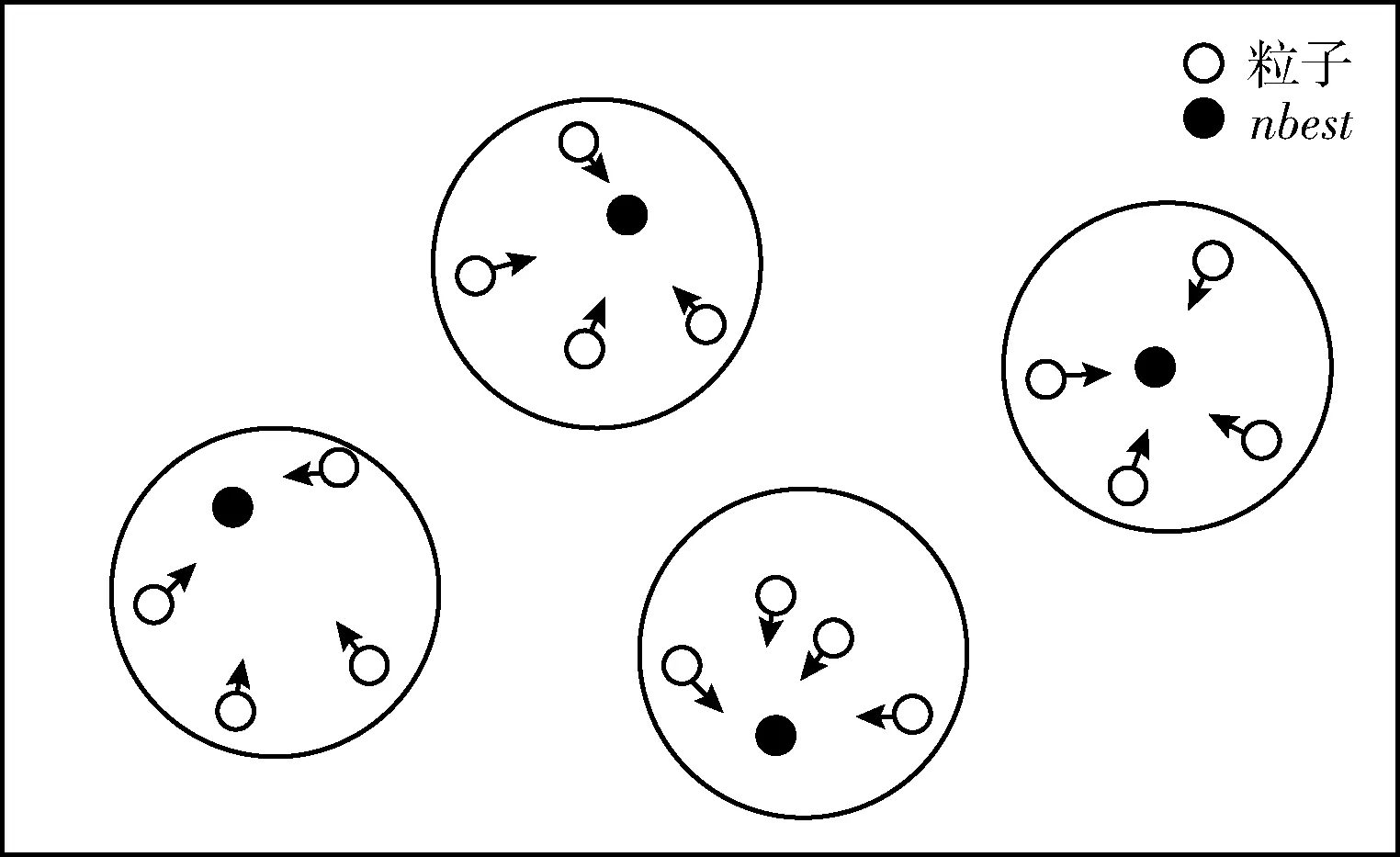
2.2 吸收机制
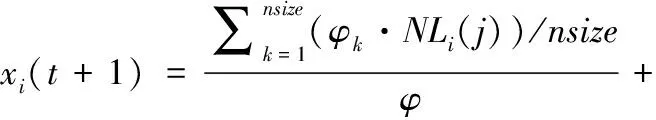

2.3 算法流程
3 实 验
3.1 测试函数



3.2 实验设计及参数设置
3.3 性能指标
3.4 实验结果






4 结束语

