边缘计算中的边缘服务器放置策略

赵兴兵，李 波，杨志军，保利勇，丁洪伟+

(1.云南大学 信息学院，云南 昆明 650000；2.云南省教育厅 教学仪器装备中心，云南 昆明 650000)

0 引 言

在移动边缘计算中，将具有计算能力和数据存储功能的边缘服务器(edge server，ES)放置在基站上，能够将核心网的部分功能下沉到网络边缘，有效降低网络传输时延。这使得研究ES放置问题具有重要意义。

目前，有关边缘服务器放置的研究较少，微云放置[1-6]和计算卸载[7,8]等都能为ES放置[9]提供一定的参考。文献[2]使用基于整数线性规划的方法对WMAN中用户和微云之间的时延进行优化，并且试图向远程云分配用户请求。文献[5]考虑将用户分配给最近的微云，以此最小化时延，并提出了基于密度优先的放置方法。文献[9，10]都对具有能量感知的ES放置进行了研究。ES放置的能耗问题包括ES的能耗和移动设备的能耗。ES的能耗主要来源于CPU，提高CPU的使用率可以优化ES的能耗；移动设备的能耗主要取决于接入时延，即优化移动设备能耗的问题本质上是优化时延的问题。文献[11]针对5G蜂窝网中的ES放置问题，提出了基于最大等效带宽的方法来最小化系统的时延开销和能量开销。文献[12]提出了基于混合整数线性规划的方法优化WMAN中ES放置的时延和负载均衡。

上述文献中，文献[1]的方法能直接用到大规模WMAN中放置ES，因为微云的放置位置一般不是基站，而为了节约部署成本，ES必须被放置在基站位置上；文献[9-11]都涉及了ES放置的能量问题，但由于用户的移动性和基站能量的无线性，优化能耗的意义较小。文献[12]提出的混合整数线性规划(MIP)在问题规模较大时表现较差。针对上述问题，本文提出一种改进遗的传算法MGA对ES进行放置，该方法对初始化种群、选择、交叉和遗传变异操作进行了改进，大幅提升了ES放置的性能。

1 ES放置模型分析

1.1 物理网络模型

用无向图G={V,E} 表示WMAN的基础设施网络，其中V=B∪C∪U。B={b1,b2,…,bm} 表示基站的集合；C={c1,c2,…,ck} 表示ES的集合；U={u1,u2…,un} 是用户的集合。E代表网络中的链路(包括基站之间的有线连接和基站与用户之间的无线连接)和逻辑分配关系。X和Y分为基站分配矩阵和ES部署矩阵，引入二进制变量xik={0,1} 表示分配关系，xik=1表示将bk分配给ci， 否则没有，xik∈X；yjk={0,1} 表示部署关系，yjk=1表示将cj放置在bk， 否则没有，yjk∈Y。 以图1的放置场景为例，其中yij=1；xie,xij,xir=1。

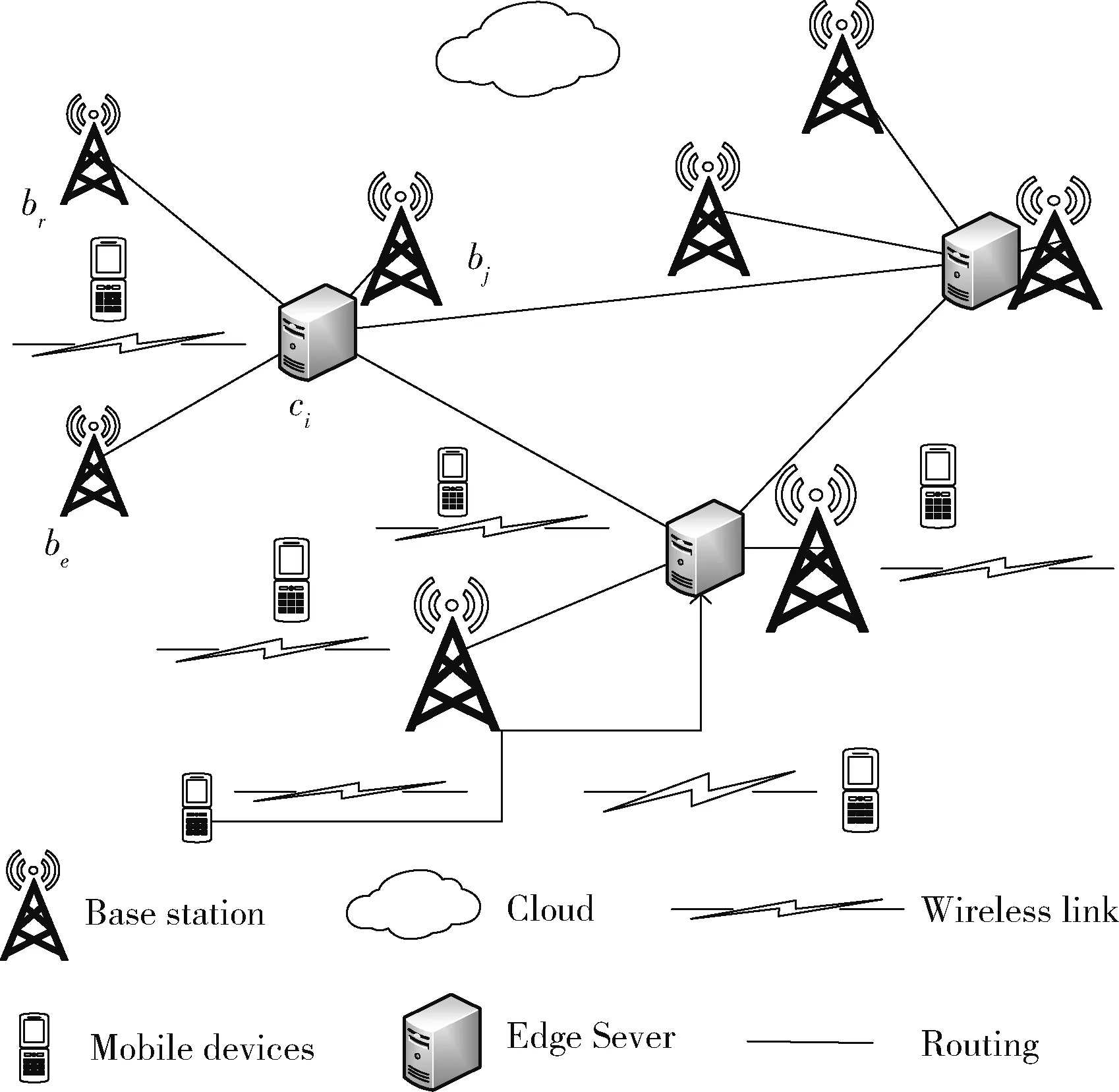
图1 ES放置场景

1.2 问题描述

基于以上分析，假设ES与某个基站共址，WMAN中的ES放置问题可定义为：在有许多基站的无向图G中，通过划分子网的思想，寻找k个合理的位置放置ES，同时考虑基站与ES之间的分配关系，使得放置后ES的平均时延最小，并且使得ES的负载均衡最优。

1.3 ES放置模型

每个子网中，用户的服务请求通过基站汇集到ES中处理，可以计算出ES的负载，如式(1)

(1)

其中，Bh表示第h个子网；wi为ui的负载。

定义1 负载均衡BL。负载均衡定义为网络中所有ES的负载的均衡程度，值越小越好。考虑经济学中用来测量收入分配差异程度的基尼系数[13]与负载均衡的相似性，引入基尼系数来计算负载均衡，其数学模型如式(2)

(2)

其中，gi为将每户收入由低到高排列后，从第1户到第i户的总收入。

同理，用每个ES的负载表示每户收入； ϖi表示将所有ES的负载从小到达排列后，从第1个ES到第i个ES的负载之和。将负载均衡定义为式(3)

(3)

ES的时延包括用户请求经基站转发到达ES，产生的本地传送时延和ES将部分负载迁移到远程云处理产生的远程传送时延。对于每个子网，ES的本地传送时延Dh表示所有用户请求经基站转发到达ES的总时延(本文不考虑移动用户请求接入基站之前的无线时延)，数学模型表示为式(4)

(4)

其中，dhj是第j个基站与其所属的第h个ES之间的距离；η为电磁波的传播速度。

对于每个ES，远程传送时延Rh是将负载中将超出W·90%的部分迁移到远程云处理产生的(假设远程云的计算能力非常强，则这部分负载产生的处理时延和排队时延可以忽略不记)，数学模型如式(5)

(5)

其中，T为将负载迁移到远程云处理所需的最大时延；W为ES负载的阈值。

(6)

其中，dh=Dh+Rh， 表示每个ES的时延。

由以上分析可知，ES放置问题是一个多目标优化问题，传统优化方法难以解决。定义一个新的指标(系统开销)，通过加权将多个优化目标转化为一个，实现目标函数降维，降低实现难度。

定义3 系统开销S。 系统开销定义为负载均衡和平均时延的加权和，其值越小，表明系统性能越好，如式(7)

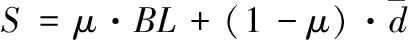
(7)

其中，μ是经验系数。根据经验，在优化过程中，负载均衡和平均时延同样重要，所以μ的值为0.5。

经过以上分析，将WMAN中的ES放置问题建模如下

(8)

其中，式(8a)是优化的目标函数。式(8b)～(8d)表示实现优化目标的约束条件；式(8b)表示所有子网能够覆盖全部用户；式(8c)表示所有基站都必须被分配给ES，且一个基站只能被分配给一个ES；式(8d)表示所有ES都被放置在基站上，且一个基站只能放置一个ES。

2 基于改进遗传算法的放置方法

2.1 传统遗传算法

GA是一种经典的种群进化算法，它模拟生物优胜劣汰的进化机制，最终得到问题的最优解。问题的可行解被抽象为染色体上基因型对应的表现型，求解优化问题的最优解等同于寻找最优的基因型。但GA存在容易陷入局部最优、收敛性差和在问题规模较大时寻优精度较低等问题，为此，本文提出MGA改善相关问题并解决大规模WMAN中的ES放置问题。

2.2 算法描述

算法主要思想：考虑大规模离散优化问题编码变量较多的问题，提出了实数编码的方式，降低了算法的实现难度与计算量；由于初始种群对于智能进化算法有较大影响，在算法开始时，采用多轮随机不重复解策略维持初始种群的多样性，扩大了全局搜索范围；在进行选择操作时，采用部分优秀父代和子代共同竞争的策略产生新的子代，保证了种群多样性，增强了算法的寻优能力；进行交叉操作时，提出了优秀父代非线性交叉节点选择算法，该算法使得MGA在早期拥有较强的全局搜索能力，在后期拥有较快的收敛速度；变异操作时，结合提出的编码方式，采用随机打乱整条染色体上基因排列的策略，能提供全新的解，进一步扩大了算法的全局搜索范围。

2.3 染色体编码

大规模WMAN中的ES放置问题本质是寻找ES到基站的映射关系，这是一个离散多目标优化问题，传统的二进制编码方法难以解决。为了减少编码变量，进而降低算法运算时间，并且易于进行交叉和变异操作，本文使用一个二维实数矩阵对染色体进行编码。

如表1所示，矩阵的形状为m×3，每一行表示一个ES的部署关系和一个基站的分配关系。每行中,第一个数据表示基站编号；第二个数据代表在此基站上放置的ES的编号，若为0，表示不放置；第3个数据是ES的编号，表示将此基站分配给ES。以表1为例，第一行表示在第一个基站上放置第一个ES；第二行表示第二个基站不放置ES并将第二个基站分配给第二个ES；第m行表示在第m个基站上放置第二个ES。

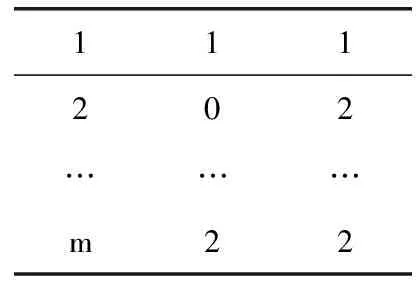
表1 染色体基因编码

因为WMAN中的ES放置问题存在约束条件，所以矩阵元素的取值必须满足以下规则：

(1)第二列元素的取值是一个整数，来自 [0,k+1]；

(2)第三列元素的取值是一个整数，来自 [1,k+1]；

(3)在每行中，如果第二列的数据不为0，则第三列的数据和第二列相同。

2.4 初始化种群

种群由一组染色体组成，每一条染色体都是问题的一组可行解；初始种群对于问题求解有重要影响。为了保证初始种群的多样性并提高搜索效率，采用多轮随机不重复解策略产生初始种群，过程如下：

(1)产生形状为N×m×3的零数组保存种群，转入步骤(2)；

(2)随机产生一个形状为m×3的数组，作为问题的一组解，与编码规则比较，若满足编码规则，转入步骤(3)；否则，重复步骤(2)；

(3)将满足编码规则的染色体加入种群，并判断当前种群的数量是否为N， 若满足，则结束；否则，转入步骤(2)。

2.5 适应度函数

适应度函数应该反映染色体的优劣程度，以便为种群进化方向提供指导。染色体的优劣程度与负载均衡和平均时延有关。将适应度函数定义为式(9)，适应度函数值越小，染色体越优秀；否则，染色体的性能越差

(9)

2.6 选择操作

对于大规模放置问题，选择操作主要考虑避免陷入局部最优与保证种群的多样性，本文使用部分父代和子代共同竞争的方式选择进入下一代的个体，过程如下：

(1)产生形状为N×m×3的零数组保存种群；转入步骤(2)；

(2)对所有染色体按照适应度函数值进行从小到大排序，保存前20%的染色体作为优秀父代染色体，转入步骤(3)；

(3)随机选择一条步骤(2)中的剩余染色体作为母亲染色体；随机在步骤(2)的优秀父代染色体中选择一条作为父亲染色体；将父亲、母亲染色体进行交叉、变异操作，产生子代染色体；转入步骤(4)；

(4)根据式(9)计算子代染色体的适应度函数值，并与步骤(2)中的所有优秀父代染色体的适应度函数值比较，若子代染色体的适应度函数值更小，则将子代染色体加入种群，转入步骤(5)；否则，重复步骤(4)；

(5)判断子代种群的数量，若为N，退出选择过程；否则，转入步骤(3)；

通过部分父代和子代共同竞争的选择策略，有效避免了陷入局部最优并保证了子代种群的多样性。

2.7 变异与遗传操作

(1)交叉操作对于算法的全局搜索能力有重要影响，结合大规模放置问题变量较多的特点，提出非线性优秀父代交叉点选择算法进行交叉操作，如下

(10)

2)根据2.6节的步骤(3)确定父亲染色体和母亲染色体，并将父亲、母亲染色体上位于交点之后的所有基因交换，交换后的父亲染色体作为子代染色体，转入步骤(3)；

3)对子代染色体按2.3节的编码规则进行检查，并进行规则化；

采用该策略，在算法前期，交叉节点的位置靠前且变化缓慢，算法有较强的全局搜索能力；随着算法进行，交叉节点的位置以更快的速度向染色体的末端移动，算法的收敛速度越来越快；并且始终与优秀父代染色体发生交叉也在一定程度上保证了收敛性。

(2)采用的变异策略为随机打乱整条染色体上的基因排列。变异操作对于算法的全局搜索能力重要意义。对于2.3节的实数编码，随机打乱染色体的基因排列将导致：①ES的位置改变；②基站与ES间的分配关系改变。所以，随机打乱整条染色体上的基因排列可以为算法提供前所未有的解。

2.8 算法流程

步骤1 按照2.3确定编码规则，按照2.5节确定适应度函数F(X)， 转入步骤2；

步骤2 初始化参数(种群数量N，权重性能参数，经验系数μ，最大远程传送时延T)，按照2.4节初始化种群，设定迭代次数L，转入步骤3；

步骤3 根据式(9)计算所有染色体的适应度函数F(X)， 按照2.6节进行选择操作，产生子代种群，转入步骤4；

步骤4 判断是否满足退出循环的条件，若满足条件，退出循环，转入步骤5；否则，转入步骤3；

步骤5 根据式(8a)计算种群中所有染色体的系统总开销，找出系统总开销最小的染色体的基因型(对应矩阵X和Y)，根据X和Y以及式(3)～式(6)计算负载均衡和平均时延。

3 仿真与结果分析型

3.1 数据集说明

本节使用来自上海市电信局的真实数据集对算法进行仿真。原始的数据集中包含大量无用信息，必须经过处理才能使用。经过处理后得到包括563 902个用户和2753个基站的有用信息，包括基站的编号、经度、纬度、15天的累计接入时长(作为负载)和用户数量等信息，部分基站信息见表2。

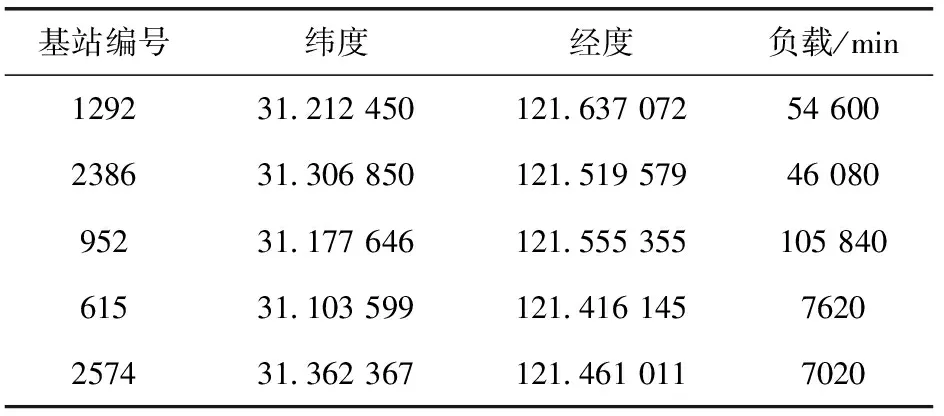
表2 部分基站的信息

3.2 仿真环境及实验设计

仿真环境配置为Intel(R) Core(TM) i7-9750H CPU 2.60 GHz处理器，Windows 10操作系统，Python 3.7版本。设置λ为0.6；N为60；T为0.5 s。为了评估本文算法的性能，选取两种比较典型的放置算法(Random[12]和K-means[14])以及文献[12]的混合整数线性规划(MIP)方法与MGA进行对比，并设计了以下两组实验：

实验1：保持ES和基站的数量之比为ρ=0.1， 不断增加基站的数量，测试各种方案的放置性能。这一组实验旨在研究各种复杂环境对放置效果的影响。尽管保持了ρ=0.1， 但是少量的基站不能完全反映WMAN中复杂的基站分布情况，所以需要对不同基站数量下的放置情况进行研究。

实验2：保持基站的数量为2753，不断增加ES的数量，测试各类方法的性能。这一组实验旨在研究基站数量一定时，不同数量的ES对放置结果的影响，能够找出最佳的ES放置比例。

3.3 实验结果分析

(1)实验1结果分析

实验1的结果如图2所示，横坐标为基站的数量。图2(a)中，当基站数量为1280时，MGA的平均时延最小，为0.13 s，相比K-Means、Random和MIP分别减少了0.16 s、0.11 s和0.08 s；可以发现，随着基站数量增加，4种算法的平均时延均基本保持不变，但MGA的平均时延是最小的，其次是MIP、Random和K-Means；在基站数量为1820时，K-Means、MIP和MGA的平均时延均有减少的趋势，分析其原因是：此时数据集中出现了一个基站分布较为密集的区域，这3种方案都在这个区域找出了较为合理的ES布局，而Random没有。

图2 ρ=0.1时放置性能随基站数量的变化

图2(b)中，随着基站数量的增加，MIP、Random和K-Means的负载均衡均有下降的趋势，这是由于ρ保持不变，随着基站数量增加，ES的数量也增加，每个基站可以分配的潜在ES的数量也增加，基站会被分配给更加合理的ES；对于MGA，随着基站数量增加，算法计算迅速增大，在一定的计算能力下，寻优精度有所下降，所以负载均衡有轻微的上升，但始终优于其余3种方案。

图2(c)中，MGA的系统开销小于MIP、Random和K-Means，相比以上各种方案，系统开销平均下降了约35.3%、45.2%和52.7%；MGA的系统开销保持在0.17左右，说明其足以应对大规模WMAN中复杂的基站分布情况。

(2)实验2结果分析

实验2的结果如图3所示，横坐标为ES的数量。图3(a)中，MGA的平均时延相比MIP、Random和K-Means平均分别减少了0.05 s、0.09 s和0.12 s；当ES的数量为280时，4种方案的平均时延都表现为上升，分析其原因为此时所有方案都将ES放置在了某些用户较为稀疏的地方，导致了这些ES的时延增加，进而影响了平均时延；放置其余数量的ES时，所有方案的平均时延均有下降的趋势，因为随着ES数量增加，ρ持续增大，每个ES都趋向于负责更近、数量更少的基站，所以平均时延下降。

图3 基站数量一定时放置性能随ES数量的变化

图3(b)中，K-Means的负载均衡随ρ增加而下降，分析其原因是：K-Means是基于距离的聚类方法，当基站数量固定时，聚类数量越多，每个聚类中的基站数量越少；而单个基站的负载相差不大；所以聚类中基站数量越少，ES的负载相差越小；其余3种方案的负载均衡都随ρ增加而上升，Random上升的原因是方法本身存在随机性，MGA和MIP上升是因为随着ρ增加，解空间迅速增大，受计算能力的限制，寻优精度下降；但是MGA的负载均衡始终优于其它方案，相比MIP、Random和K-Means平均分别下降了19.1%、18.9%和18.6%。

图3(c)中，MGA相比MIP、Random和K-Means系统开销平均下降了约54.1%、42.9%和20.6%；4种方案的性能曲线的变化都在ES的数量为280时开始变得缓和，说明此后再增加ES的数量带来的回报开始减少。所以，对于数据集对应的真实WMAN，保持ES与基站的数量之比ρ=280/2753=0.1017时，ES放置有最大的回报率。

3.4 分析适应度函数的权重性能系数

适应度函数F(X)的权重性能系数λ不同于计算系统开销时的经验系数μ。λ对MGA的寻优精度有重要影响。采用实验的方法对λ的最佳取值进行研究，设置基站数量为500，ES的数量为50,运行20次程序，然后取平均值，得到图4。由图4可知，λ=0.6时，MGA的寻优效果最好。(注：本文其它实验的λ均为0.6)

图4 系统开销随λ的变化

3.5 收敛性分析

设置基站数量为500，ES的数量为50，λ=0.6，运行程序20次，然后取平均值得到图5。由图5可知，MGA在前600次迭代过程中收敛速度较快，迭代1400次后算法的系统开销保持不变，找到全局最优解。使用MGA使系统开销从0.208下降到0.172，下降了约17.3%，并在后期保持不变。

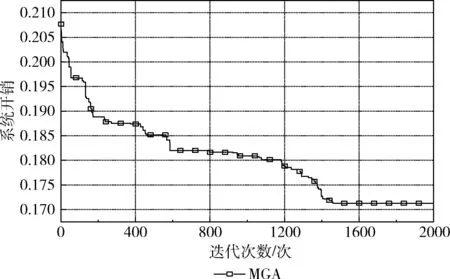
图5 系统开销的收敛曲线

4 结束语

针对移动边缘计算中WMAN环境下的ES放置问题进行了研究。对ES的放置场景进行了介绍，通过划分子网的思想将其建模为优化负载均衡和平均时延的多目标优化问题。提出一种改进的遗传算法解决该优化问题。MGA在编码、初始化种群、选择、交叉和变异等操作方面均做了较大改进，增强了算法的全局搜索能力，保证了算法的收敛性。基于真实数据集的仿真结果表明，相比于其它算法，当ρ在0.036到0.167内变化时，MGA能够很好解决复杂WMAN中的ES放置问题，对于解决其它大规模离散优化问题也有一定的帮助。ES放置问题是一个NP难的多目标优化问题，随着基站数量增加，解空间急剧增大。传统优化算法难以解决，未来会将考虑使用多目标优化算法，其能够快速找到Pareto最优解，有效解决问题。