桥上无缝线路断轨力深化研究
张 泽,黄晨睿
(1.中铁第四勘察设计院集团有限公司,武汉 430063; 2.长安大学长安都柏林国际交通学院,西安 710021)
1 概述
无缝线路将标准长度钢轨焊接为长钢轨线路,在我国得到了广泛应用[1-2]。桥上无缝线路梁轨相互作用复杂,由于钢轨焊接接头质量、施工时锁定轨温超过设计锁定轨温、运营养护作业不当等原因,在秋冬季节昼夜温差较大的情况下,钢轨内部将承受反复的拉压荷载,当钢轨温度力超过钢轨强度限值时,钢轨很容易在焊缝处发生折断[3]。
当桥上无缝线路发生断轨时,储存在钢轨内部的巨大温度力将通过轨道结构或道床传递到桥梁,进而再传递到桥梁墩台,桥梁墩台断轨力往往较大,影响桥梁专业设计。针对桥上无缝线路断轨力,相关学者对其进行了研究。龚小平[4]考虑相邻钢轨影响,推导了桥上无缝线路断轨力计算公式,并采用有限元手段对公式进行了计算验证;徐庆元[5-7]考虑高速铁路空间特性,建立了高速铁路断轨力空间计算模型,研究了计算模型对钢轨断缝值的影响;闫子权[8]建立了桥上无缝线路三维计算模型,研究了单线桥梁单根钢轨折断与两根钢轨同时折断桥梁墩台断轨力的区别;陈伟新[9]计算分析了东江特大桥桥上不同断轨位置下的墩台断轨力。
根据TB 10015—2012《铁路无缝线路设计规范》(以下简称“《无缝线路规范》”)及计算模型计算的断轨力往往较实际情况大,本文在吸收相关学者研究成果的基础上,建立了钢轨-桥梁-桥梁墩台三维有限元空间力学计算模型。采用建立的模型,考虑不同轨道类型、不同简支梁跨长,分别计算研究了双线4根钢轨折断,1根钢轨折断其他钢轨不折断工况下,桥上无缝线路断轨力计算公式修正值[10],相关研究成果对于更精准计算桥上无缝线路断轨力具有较大意义,可更好的指导我国桥梁合理设计,并为后续规范修编提供研究基础。
2 常规断轨力计算方法
《无缝线路规范》[11]中桥上无缝线路固定区断轨力计算如下
F断=r×L
(1)
式中,r为线路纵向阻力;L为桥梁梁长。
当计算值大于固定区钢轨温度力时,断轨力采用固定区温度力。
目前,桥上无缝线路纵向力计算采用双线性阻力模型[12-13],以无砟轨道常阻力扣件为例,线路纵向阻力示意如图1所示。
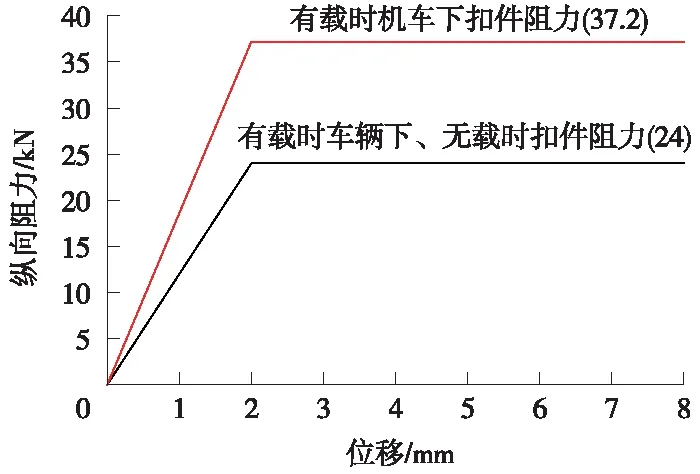
图1 桥上无缝线路纵向阻力示意
《无缝线路规范》中的计算公式有3个假定:①计算跨长内的所有非线性阻力弹簧均超过其屈服位移;②在同一位置处所有钢轨同时折断;③钢轨断轨力全部传递到桥梁墩台上。
但实际上,我国地域广阔,不同地区温差较大,采用此种算法,对于温暖地区,断轨力将比实际取值要大。即使对于我国温降最大地区,当梁长足够长时,也只有断轨两侧一定范围内的线路阻力可以达到屈服,因此,对于跨度较长的简支梁,采用此公式计算的断轨力也会比实际更大。此外,钢轨在低温下折断,一般只有1根钢轨折断,双线桥梁在同一位置处4根钢轨同时折断的概率很小,公式计算的断轨力也要较实际更大。
为更准确地计算墩台断轨力,国内大多采用线-桥-墩一体化梁轨相互作用模型,模型可以考虑线路非线性阻力特性,但此模型仅包含1根钢轨[14-16]。对于单线桥梁,计算结果为2根钢轨同时折断,对于双线桥梁,计算结果为4根钢轨同时折断。1根钢轨折断时,其断轨力并不会全部传递到桥墩上,相邻钢轨也会承担一定的断轨力,采用常规断轨力计算模型仍无法考虑1根钢轨折断而相邻钢轨不折断对其的影响。因此,桥上无缝线路断轨力计算模型需深化研究。
3 计算模型及参数
3.1 计算模型
为深化桥上无缝线路断轨力取值,考虑多线钢轨间的耦合关系,基于梁轨相互作用理论[1,17-19],建立了线-桥-墩一体化三维有限元计算模型,以简支梁为例,二维及三维实体模型分别如图2、图3所示。
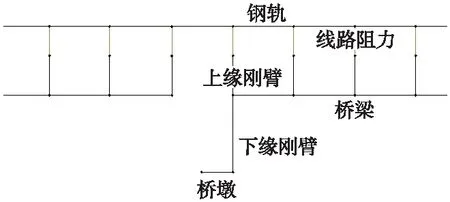
图2 线-桥-墩一体化二维有限元计算模型主视
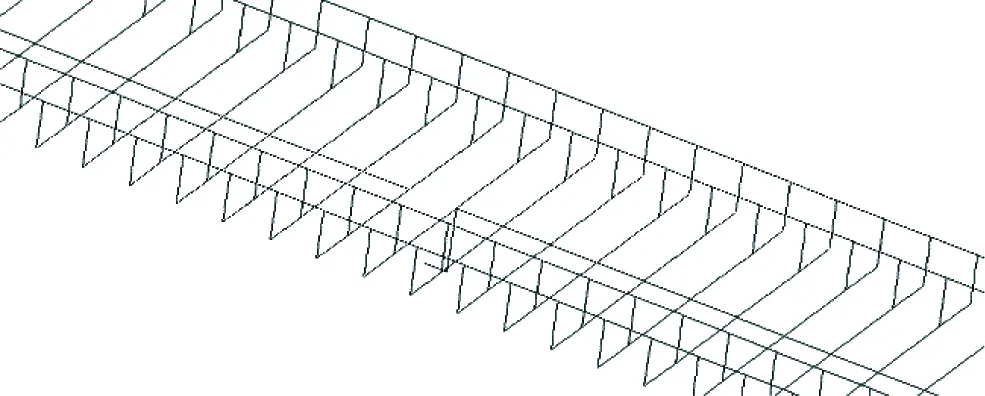
图3 线-桥-墩一体化三维有限元计算模型主体
双线模型共建立4根钢轨,简支梁两边各为100 m路基。钢轨、桥梁采用Beam4空间梁单元模拟,线路纵向阻力单元采用Combin39非线性弹簧单元模拟,桥梁墩台采用Combin14线性弹簧单元模拟。桥梁上缘刚臂采用刚体单元模拟,单元长度为简支梁梁面至桥梁中性轴的距离,本处简支梁为常截面,故在模型中刚臂单元长度均相同。桥梁下缘刚臂单元长度为简支梁墩顶至桥梁中性轴的距离,用于精确计算桥墩受力。
当双线桥梁一根钢轨折断时,一部分断轨力通过桥梁传递至桥梁墩台,一部分断轨力被邻线钢轨承担,相比常规计算模型,三维空间计算模型计算结果更加接近实际。
3.2 计算参数
简支梁跨数取10跨,跨长分别为16,20,24,32,40 m,简支梁两端各取100 m路基,桥梁布置如图4所示。

图4 桥跨布置示意
简支梁上铺设常阻力扣件,计算断轨力时,根据相关研究成果,桥梁跨中断轨时,钢轨断缝值及桥墩断轨力最为不利,因此,断轨位置选择在桥梁中部折断。我国南北差异较大,为获得我国最不利温降幅度,对《无缝线路规范》中所有城市的历史最不利温降幅度进行统计,其中,我国东北漠河地区钢轨最大温降60.8 ℃,为最不利地区,因此,计算时钢轨温降取60.8 ℃。
4 断轨力取值研究
本节研究16,20,24,32,40 m简支梁在不同断轨根数下,无砟轨道及有砟轨道墩台断轨力随墩刚度的变化规律,并分析单根钢轨折断工况下与理论计算公式的差异,为《无缝线路规范》修订提供依据。
4.1 计算工况
分别计算不同断轨根数、不同轨道类型及简支梁纵向墩刚度下的墩台断轨力,共计44种工况,计算工况如表1所示。

表1 计算工况
4.2 计算结果
4.2.1 双线4根钢轨折断
当双线桥梁在同一位置处4根钢轨同时折断时,无砟轨道、有砟轨道墩台断轨力随墩刚度变化分别如表2、表3所示。
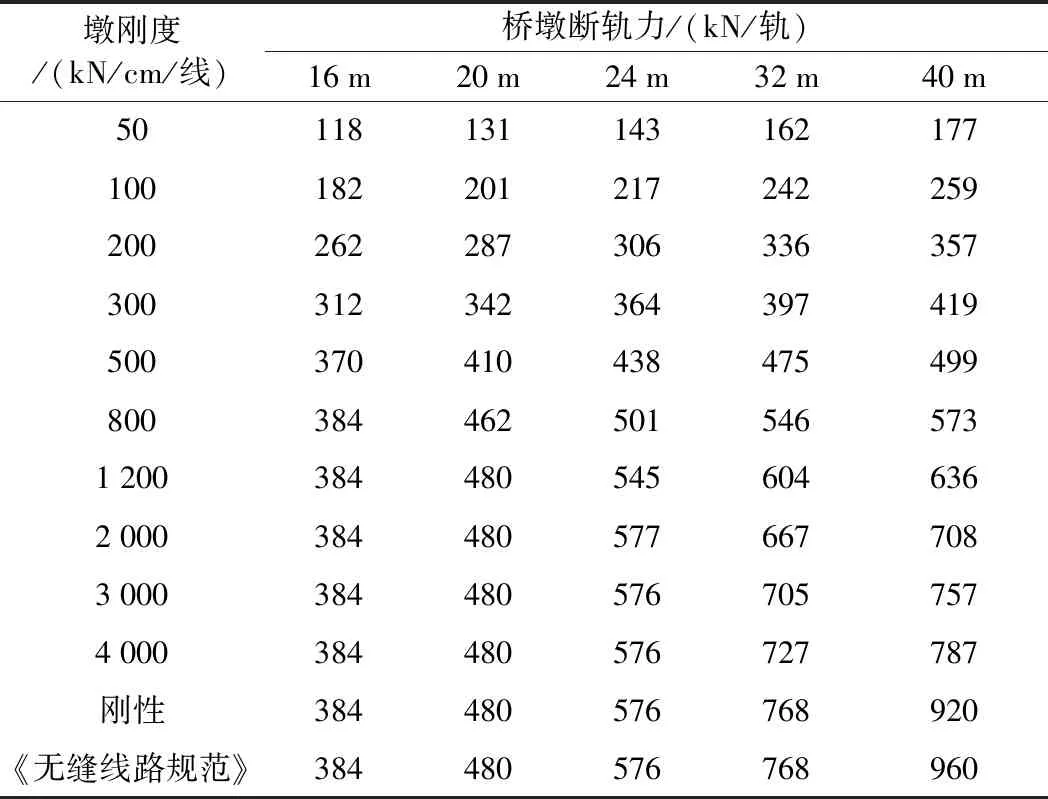
表2 无砟轨道简支梁墩台断轨力计算
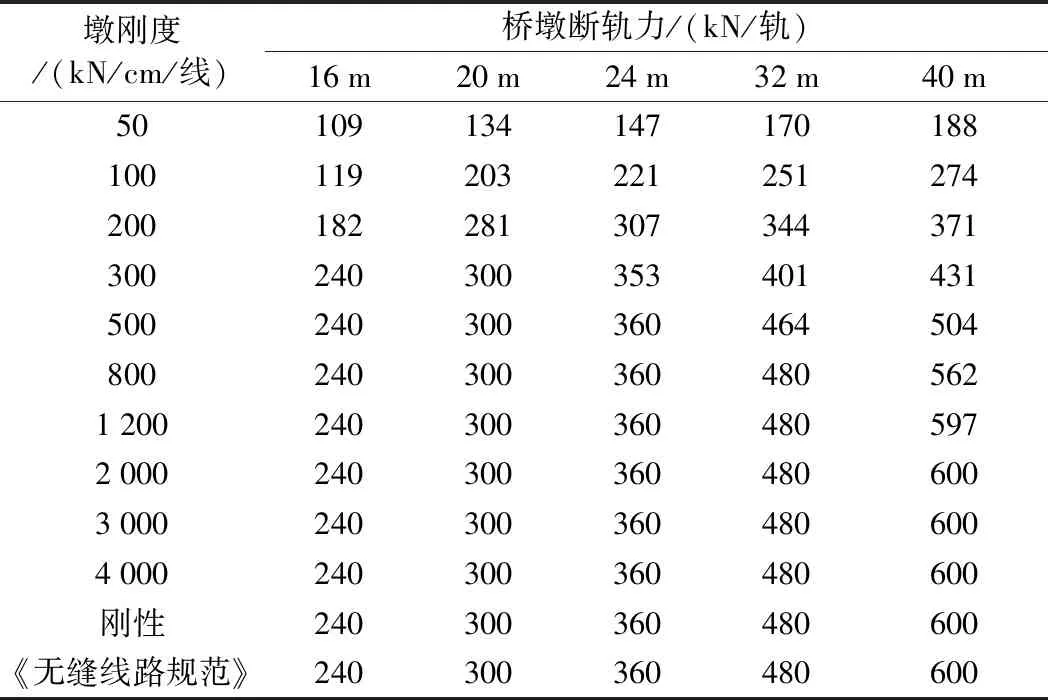
表3 有砟轨道简支梁墩台断轨力计算
无砟轨道、有砟轨道墩台力随着墩刚度变化如图5、图6所示。

图5 无砟轨道墩台断轨力随墩刚度变化曲线

图6 有砟轨道墩台断轨力随墩刚度变化曲线
从图5、图6可以看出,在我国温降最大区域,当双线桥梁4根钢轨在同一位置处全部折断时,随着墩刚度增加,墩台断轨力先快速增加,之后增加幅度变缓,最后趋于一定值。
从表2可知,对于无砟轨道,跨长为32 m及以下简支梁在墩刚度为刚性时的墩台断轨力与《无缝线路规范》相同,跨长为40 m简支梁在墩刚度为刚性时的墩台最大断轨力为920 kN,小于《无缝线路规范》计算值960 kN。主要原因是即使在我国最大温降地区,钢轨巨大的断轨力也无法使40 m简支梁上所有阻力弹簧均屈服,即伸缩区长度要小于40 m。由此可以推断,当跨长更长时,计算的断轨力均会比《无缝线路规范》计算值更小。
对于有砟轨道,计算的不同跨长简支梁墩台断轨力均与《无缝线路规范》值相同,《无缝线路规范》具有较好的适应性。但以40 m跨长简支梁为例,当墩刚度为2 000 kN/cm/线时,墩台力才与《无缝线路规范》计算值相同。TB 10621—2014《高速铁路设计规范》[20]中,40 m跨长简支梁最小墩刚度限值为340 kN/cm/线,远小于本文计算值2000 kN/cm/线,由此可以看出,《无缝线路规范》计算的断轨力是相对保守的。
4.2.2 双线单根钢轨折断
当双线桥梁在同一位置处仅有单根钢轨折断,而相邻其他钢轨不折断时,无砟轨道、有砟轨道墩台断轨力随墩刚度变化分别如表4、表5所示。
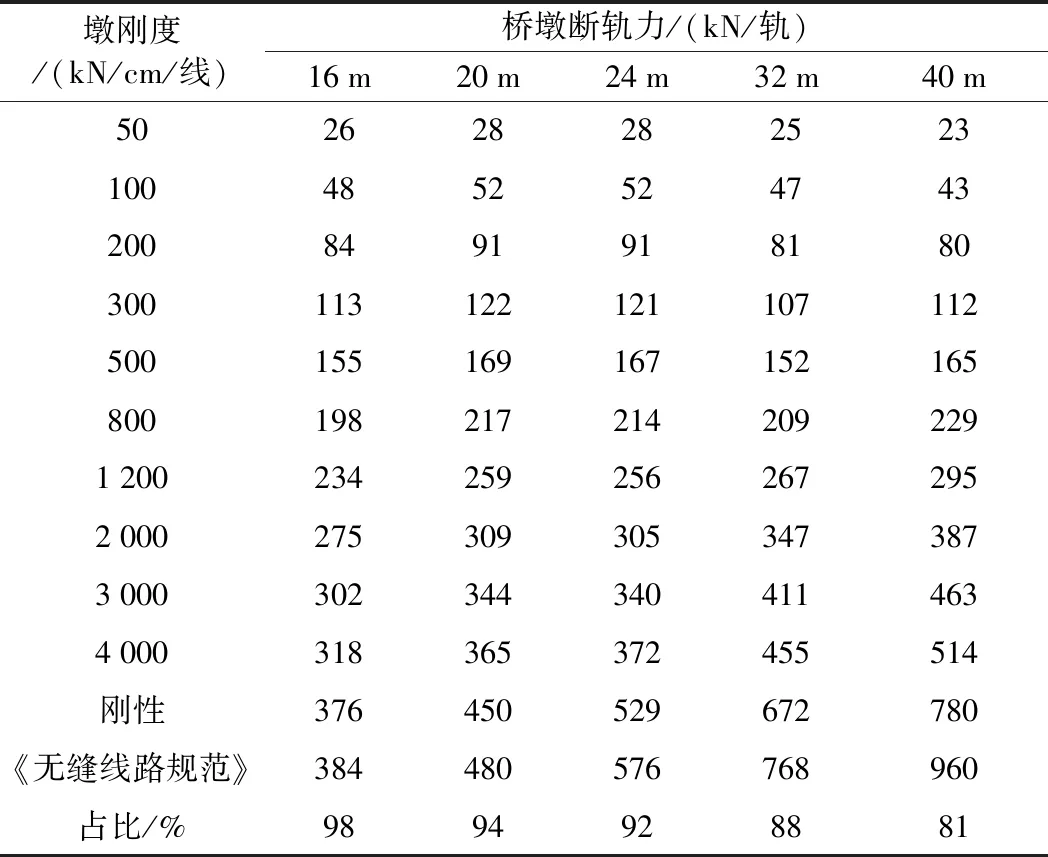
表4 无砟轨道简支梁墩台断轨力计算
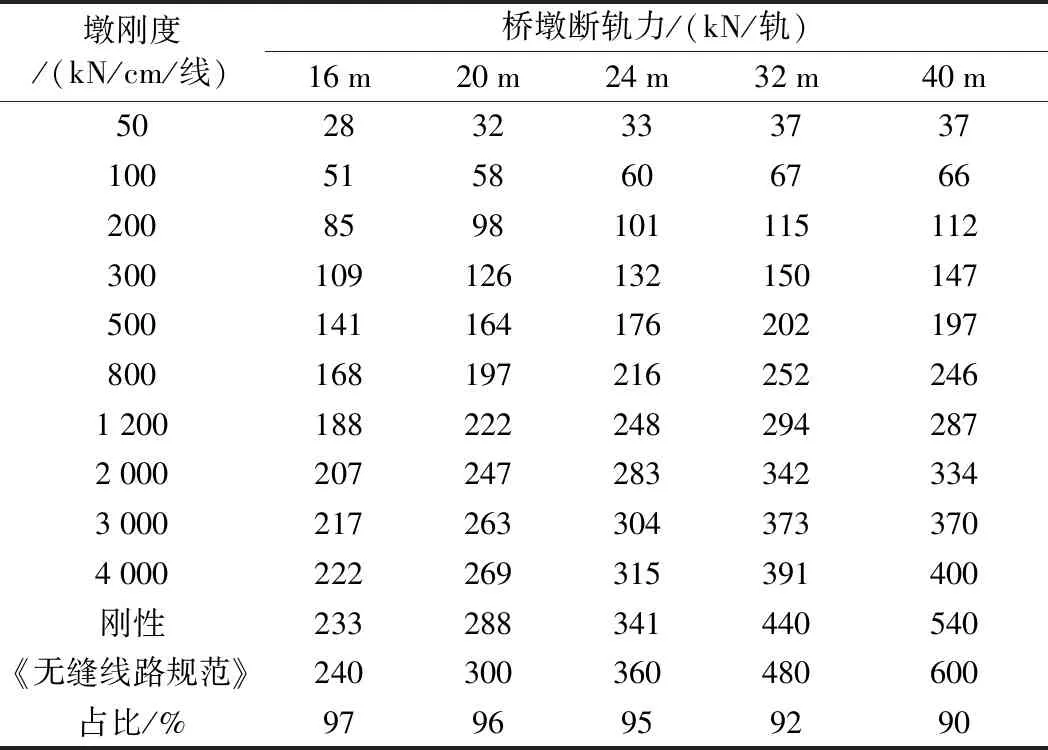
表5 有砟轨道简支梁墩台断轨力计算
墩刚度为500 kN/cm/线,无砟轨道32 m简支梁单根钢轨折断工况下,断轨侧及非断轨侧钢轨断轨力及位移分别如图7、图8所示,对比两图可以看出,当双线桥梁1根钢轨折断时,断轨侧钢轨在断轨位置处的断轨力为0,但在同一位置非断轨侧,钢轨纵向力可达1 337 kN,大于钢轨温度力1 166 kN。由此可以看出,当双线桥梁1根钢轨折断时,其巨大的断轨力并不会完全传递到桥梁墩台上,由于邻线非折断钢轨的影响,有很大一部分力将由邻线钢轨承担。
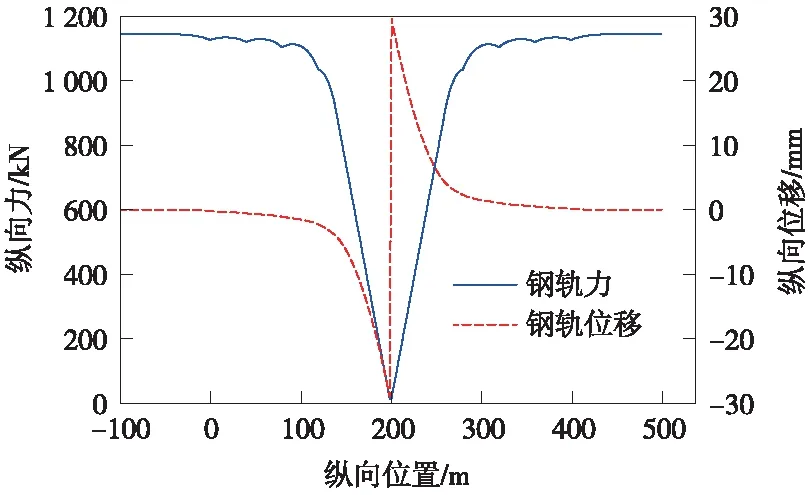
图7 断轨侧钢轨纵向力及位移计算

图8 非断轨侧钢轨纵向力及位移计算
对比分析表4和表2、表5和表3可以看出,在相同墩刚度下,双线桥梁4线钢轨折断时计算的钢轨断轨力要大于单根钢轨折断工况,且墩刚度越小,单根钢轨折断断轨力要比4根钢轨折断断轨力更小,表明墩刚度越小,断轨力由邻线所承担的力越大,传递到墩台上的力越小。当墩刚度不断增加到接近刚性时,墩台断轨力不再改变,且计算的断轨力由于邻线钢轨的承担作用,均小于《无缝线路规范》计算值。
表4、表5中,“占比”为墩刚度为刚性时的断轨力与《无缝线路规范》比值,对比可知,无砟轨道16 m简支梁断轨力为规范值的98%,40 m简支梁断轨力为规范值的81%;有砟轨道16 m简支梁断轨力为规范值的97%,40 m简支梁断轨力为规范值的90%。墩刚度为刚性时,随着简支梁跨长增加,单轨折断断轨力与规范值相比,占比越小。相同简支梁跨长下,无砟轨道比有砟轨道占比小。
5 断轨力计算公式修正
根据以上计算可知,当墩刚度接近刚性时,墩台断轨力将为一定值,且单轨折断断轨力始终小于《无缝线路规范》计算值。因此,考虑相邻钢轨不折断影响,《无缝线路规范》中断轨力计算公式可按下式修正
F断=a×r×L
(2)
式中,a为断轨力折减系数,按表6取值。

表6 断轨力计算公式修正系数
6 结论
考虑单根钢轨折断,其他钢轨不折断的影响,建立了钢轨-桥梁-桥梁墩台三维有限元空间力学计算模型。考虑不同轨道类型、不同简支梁跨长,对桥上无缝线路墩台断轨力进行了深化研究,在此基础上,提出了桥上无缝线路断轨力计算公式修正系数。研究得到以下结论。
(1)以我国温降最大地区漠河为例,双线桥梁4根钢轨折断时,当墩刚度接近刚性时,无砟轨道40 m及以上简支梁断轨力小于《无缝线路规范》计算值。
(2)当桥梁墩刚度取《高速铁路设计规范》最小限值时,计算的无砟轨道及有砟轨道墩台断轨力要远小于《无缝线路规范》计算值,即采用公式计算的断轨力为极不利值。
(3)一根钢轨折断,其他钢轨不折断时,钢轨断轨力将有较大的一部分传递到相邻钢轨上,桥梁墩台上断轨力小于四根钢轨同时折断的情况,当墩刚度接近刚性时,断轨力将为一定值。
(4)根据墩刚度为刚性时的墩台断轨力,提出了钢轨断轨力计算公式修正值,简支梁跨长越长,修正系数越小,相同简支梁跨长下,无砟轨道修正系数小于有砟轨道。
(5)当温度较低、桥梁跨度较长、墩刚度较小时,钢轨在断轨后的无缝线路伸缩区将较短,用公式计算的断轨力将大大超过其实际值,且《无缝线路规范》计算公式未考虑墩台刚度影响,因此在进行墩台力计算时,可采用本文提出的修正计算公式。

