客货共线铁路弹性支承块式无砟轨道结构极限状态设计法研究
陈 潇
(中铁第四勘察设计院集团有限公司,武汉 430063)
基于可靠度理论的极限状态设计法已经成为国际工程结构设计的主流方法[1-2]。我国铁路工程设计方法正在从容许应力法向极限状态法转换[3-5],铁路轨道自2011年起开展了系列研究课题和试设计工作[6-7],于2018年正式发布Q/CR 9130—2018《铁路轨道设计规范(极限状态法)》[8]。然而,前期研究工作主要针对高速铁路典型无砟轨道结构型式,如CRTSⅠ、Ⅱ、Ⅲ型板式及双块式无砟轨道[9-10],缺乏对客货共线铁路弹性支承块式无砟轨道极限状态设计法的充分研究[11]。客货共线铁路等级、运营条件及轨道类型与“转轨”研究对象不同,急需对客货共线弹性支承块式无砟轨道极限状态设计方法进行研究。
以设计速度160 km/h客货共线铁路为对象,结合弹性支承块式无砟轨道结构特点,分析弹性支承块式无砟轨道结构计算模型和加载方式,提出弹性支承块式无砟轨道极限状态设计表达式及分项系数,并结合衢宁铁路弹性支承块式无砟轨道结构进行道床板极限状态法试设计。
1 计算模型与加载方式
以客货共线Ⅰ级铁路、设计速度160 km/h、运营货车轴重25 t为对象,隧道内弹性支承块式无砟轨道由钢轨、预埋铁座式弹性可调扣件、预制混凝支承块、支承块下弹性垫板、橡胶套靴及道床板等组成,轨道结构高度为600 mm,如图1所示。
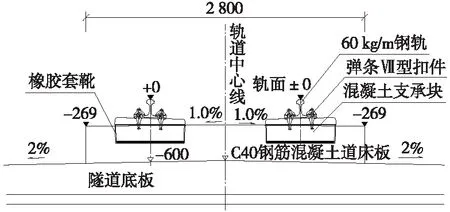
图1 隧道内弹性支承块式无砟轨道结构断面示意(单位:mm)
弹性支承块式无砟轨道结构区别于高速铁路CRTSⅠ、Ⅱ、Ⅲ型板式及双块式无砟轨道的特点主要是低刚度和可修复性[12-13]。弹性支承块式无砟轨道结构垂直弹性由轨下和块下双层弹性橡胶垫板提供;橡胶套靴则提供了轨道的纵、横向弹性变形,使这种无砟轨道在承载、动力传递和振动能量吸收方面接近坚实均匀基础上的碎石道床轨道。由于套靴的隔离作用,支承块可从道床结构中取出,使运营中损伤的弹性支承块系统具有可修复性。
Q/CR 930—2018《铁路轨道设计规范(极限状态法)》条文说明中规定:“列车竖向荷载引起的主体结构中的弯矩或应力,一般按‘弹性地基梁-板理论’进行计算”,对非板式轨道的模型和加载方式未明确。下文对模型是否考虑支承块、橡胶套靴、垫板,以及加载方式进行分析。
1.1 计算模型
钢轨采用60 kg/m、U75V无螺栓孔新钢轨;扣件类型采用弹条Ⅶ型扣件,根据TJ/GW 152—2016《客货共线铁路隧道内弹性支承块式无砟轨道用部件暂行技术条件》中规定,轨下垫板的静刚度为100~120 kN/mm,动静刚度比考虑为2.0;支承块为C50混凝土结构;橡胶套靴刚度为200~300 kN/mm,块下垫板刚度为60~90 kN/mm,动静刚度比考虑为1.8;道床板分块浇筑,板长为6.58 m,宽为2.8 m,采用C40混凝土现场浇筑。列车竖向荷载标准值Pk=2Pj,Pj为静轮重,取设计静轴重的一半,则Pk=250 kN。
分别建立不考虑和考虑支承块结构模型,如图2、图3所示。
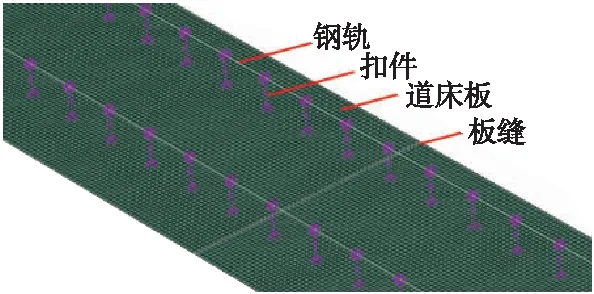
图2 不考虑支承块结构模型

图3 考虑支承块结构模型
加载方式采用单轴双轮加载[14],两种计算模型的道床板弯矩结果如表1所示。

表1 道床板弯矩最大值 kN·m/m
由表1可知,不考虑支承块模型计算所得的弯矩值明显大于考虑支承块模型的弯矩值:纵向最大正、负弯矩值分别增大2.68倍和1.01倍;横向最大正、负弯矩值分别增大1.82倍和0.93倍;正弯矩增大更为明显。
可见,支承块结构(含橡胶套靴和块下垫板)对列车荷载作用下道床板弯矩值影响较大,从而影响道床板的理论计算配筋结果,因此,建议在客货共线铁路轨道弹性支承块式无砟轨道结构设计时,计算模型考虑支承块、块下垫板、橡胶套靴。
1.2 加载方式
加载方式考虑单轴双轮、双轴四轮(两轮对间距2.5 m)、三轴六轮(轮对间距为2.5 m、2 m)3种加载方式,如图4所示。根据列车荷载的作用位置,选取板中、板边、板缝3种工况对模型进行计算,以便得到最不利加载位置的计算结果。

图4 加载方式
根据计算结果,单轴双轮、双轴四轮和三轴六轮3种方式的最不利加载位置分别为板中、板边和板缝,道床板弯矩结果见表2。

表2 不同加载方式道床板弯矩计算结果 kN·m/m
由表2可以看出,对于道床板板底正弯矩,随着加载轮对增加,板底正弯矩有下降趋势,列车荷载采用单轴双轮加载且作用在板中时,板底正弯矩最大;对于道床板板顶负弯矩,随着加载轮对增加,板顶负弯矩有上升降趋势,列车荷载采用三轴六轮加载且作用在板缝时,板顶负弯矩最大。
2 极限状态设计表达式及分项系数
2.1 功能函数
隧道内弹性支承块式无砟轨道为单元结构,承载能力极限状态为道床板正截面抗弯承载力满足要求,正常使用极限状态为最大道床板裂缝宽度满足要求。
洞口小于200 m隧道内无砟轨道主要考虑列车荷载、温度作用,洞口大于200 m隧道内无砟轨道仅考虑列车荷载。
道床板承载能力功能函数为
G(X)=MR-Md-Mt
(1)
式中,MR为道床板承载力的随机变量;Md为道床板列车荷载作用效应的随机变量;Mt为道床板温度梯度作用效应的随机变量。
正常使用功能函数为
G(X)=wlim-w
(2)
式中,wlim为道床板裂缝宽度限值;w为道床板计算裂缝宽度。
2.2 随机变量概率模型及统计参数
(1)列车荷载效应
无砟轨道在列车荷载作用下的效应,按有限元计算确定。考虑列车轮载、扣件刚度、块下垫板刚度、线下基础刚度、道床板弹性模量为基本随机变量(表3),通过点估计有限元法[15],采用立方正态分布来描述随机参数下弹性支承块式无砟轨道结构25 t轴重列车荷载效应统计特征,列车荷载作用下,道床板弯矩的前四阶统计矩[16]如表4所示。

表3 基本随机变量概率分布及统计特征参数

表4 列车荷载效应统计参数
(2)温度梯度作用效应
根据前期转轨研究对无砟轨道温度梯度的观测数据,其设计基准期的最大值分布为极值Ⅰ型分布,正温度梯度变异系数为0.158,负温度梯度变异系数为0.275。根据Q/CR 9130—2018《铁路轨道设计规范(极限状态法)》,最大正温度梯度为90 ℃/m,最大负温度梯度为45 ℃/m,板厚350 mm的修正系数为0.89,可求得最大正温度梯度作用效应标准值90.92 kN·m/m,最大负温度梯度作用效应标准值45.46 kN·m/m。
(3)抗力参数
结构抗力的概率分布及统计参数一般应根据其几何参数制作出实体模型,并通过试验确定。对于承载能力极限状态的强度检算,抗力也可以用弯矩来表示。对于纯弯构件,最大可承受弯矩与钢筋抗拉强度成正比,因而,最大可承受弯矩的变异系数可取为与钢筋抗拉强度相同。根据铁科院《铁路工程结构极限状态法设计关键抗力参数动态采集与分析》中的研究成果,HPB300、HRB400的力学性能统计分布建议值见表5。

表5 钢筋力学性能统计参数取值
2.3 道床板极限状态法分项系数计算
以距隧道洞口小于200 m范围弹性支承块式无砟轨道道床板的极限状态法设计为例,荷载效应考虑温度梯度效应和列车作用效应。
(1)承载能力极限状态法
客货共线铁路轨道弹性支承块式无砟轨道道床板承载力极限状态法设计表达式为
γdMdk+γtMtk≤φRMR
(3)
式中,γd,γt分别为列车荷载效应分项系数、温度梯度作用效应分项系数;φR为道床板截面抵抗弯矩分项系数。对安全等级为二级的道床板进行极限状态设计时,其承载能力极限状态下的目标可靠指标为βT=3.7。
以道床板纵向正截面为例,采用极限状态法进行设计并配置钢筋,作用组合为列车荷载正弯矩效应+正温度梯度作用效应。采用一次二阶矩法[17]确定设计表达式中分项系数,计算求得的道床板分项系数设计表达式为
0.953MR≥1.161Mdk+0.47Mtk
(4)
(2)正常使用极限状态
对道床板进行正常使用极限状态(裂缝宽度不超过限值)设计时,功能函数为
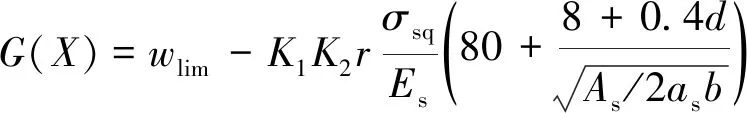
(5)
其中

(6)
上式不能反映抵抗弯矩和作用弯矩效应的直接关系,但由于采用极限状态法设计截面配筋时,保持道床板尺寸、混凝土等级及钢筋种类不变,式中除受拉钢筋面积与直径以外的其他参数均已知(保护层厚度为35 mm,h0、as可根据截面高度与钢筋直径计算),因此,将正常使用极限状态方程等价于
G′(X)=f(As,d)-Mdk-Mtk≥0
(7)
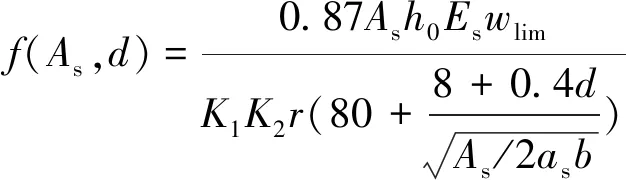
(8)
极限状态法设计表达式为

(9)
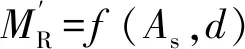
以道床板板底横向裂缝宽度不超过限值的设计为例,采用极限状态法进行设计并配置钢筋,作用组合为常用列车荷载正弯矩效应+常用正温度梯度作用效应。采用一次二阶矩法确定设计表达式中分项系数,计算求得的道床板分项系数设计表达式及等效抵抗弯矩值为
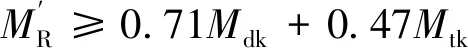
(10)
(3)道床板设计分项系数取值建议
由于规范设计表达式形式对结构抗力(即道床板承载力)不取分项系数,仅对作用效应取分项系数,因此,将上述分项系数表达式中MR的系数转化为1,仅作用效应取分项系数。分别对道床板纵横向上、下层分析极限状态法设计分项系数,列于表6。
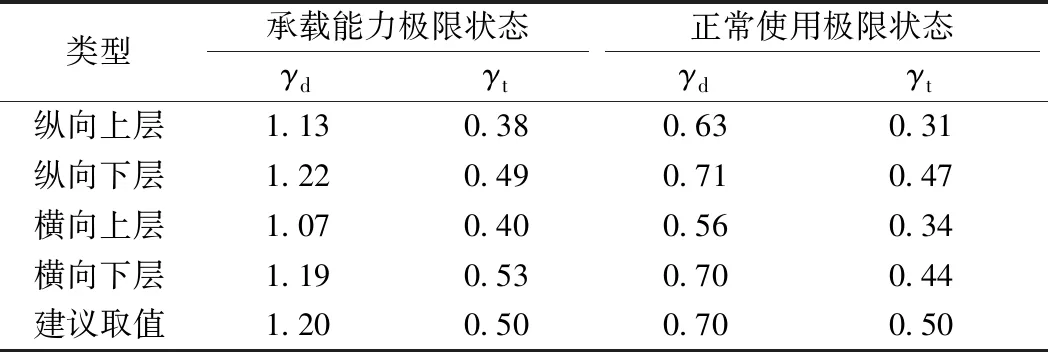
表6 道床板极限状态法设计分项系数
3 极限状态法试设计
以衢宁铁路隧道内弹性支承块式无砟轨道结构为对象,轨道结构如图1所示,采用极限状态法和容许应力法分别对其道床板进行配筋计算,道床板混凝土强度等级为C40,为分块结构,宽2 800 mm,厚351 mm,采用HRB400级钢筋。
隧道内弹性支承块式无砟轨道为单元结构,承载能力极限状态设计时,道床板按受弯构件进行正截面受弯承载力设计[19-20];正常使用极限状态设计时,道床板按受弯构件计算最大裂缝宽度。
3.1 距洞口小于200 m隧道地段
洞口小于200 m的隧道内无砟轨道主要考虑列车荷载、温度作用,承载能力和正常使用极限状态设计作用分项系数根据本文建议取值。道床板配筋计算结果如表7所示。
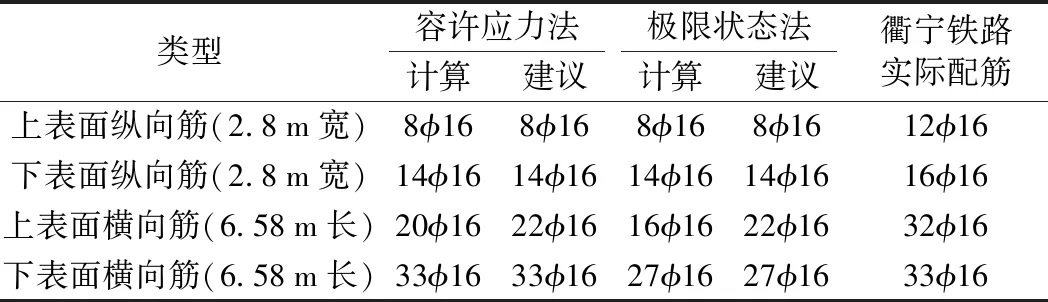
表7 计算配筋与衢宁铁路配筋对比(距洞口小于200 m)
(1)理论计算配筋比较
对于隧道地段(距离洞口小于200 m)的弹性支承块式无砟轨道道床板,极限状态法计算的纵向配筋结果与容许应力法计算配筋一致;横向上表面和下表面配筋分别减少4φ16 mm和6φ16 mm,减少20%和18%。
(2)建议配筋量比较
距洞口小于200 m隧道地段的弹性支承块式无砟轨道道床板,考虑最小配筋率后,极限状态法计算的纵向配筋结果与容许应力法计算配筋一致;横向上表面和下表面配筋分别减少2φ16 mm和6φ16 mm,减少10%和18%。
采用极限状态法建议的配筋与衢宁铁路纵横向钢筋均减少,纵向钢筋上下层分别减小4根、2根,横向钢筋上层减小10根、下层减少6根;采用容许应力法的建议配筋与衢宁铁路纵横向钢筋均减少,纵向钢筋上下层分别减小4根、2根,横向钢筋上层减小10根、下层相同。
3.2 距洞口大于200 m隧道地段
洞口大于200 m的隧道内无砟轨道仅考虑列车荷载,分项系数按本文建议取值。道床板配筋计算结果如表8所示。

表8 计算配筋与实际项目配筋对比(距洞口大于200 m)
(1)理论计算配筋比较
对于隧道地段(距离洞口大于200 m)的弹性支承块式无砟轨道道床板,极限状态法计算的纵横向配筋结果比容许应力法计算配筋均有减少:纵向上表面和下表面配筋分别减少1φ16 mm和2φ16 mm,均减少30%;横向上表面和下表面配筋分别减少1φ14 mm和3φ14 mm,减少14%和23%。
(2)建议配筋量比较
距洞口大于200 m隧道地段的弹性支承块式无砟轨道道床板,考虑最小配筋率要求后,采用极限状态法计算的纵横向配筋与容许应力法一致,均为最小配筋率要求。
两种方法建议配筋与衢宁铁路实际配筋相比,纵向钢筋上层减小3根、下层减少7根,横向钢筋上层减小8根、下层减少10根。
4 结论
结合客货共线铁路弹性支承块式无砟轨道结构特点,分析了弹性支承块式无砟轨道结构计算模型和加载方式,提出了弹性支承块式无砟轨道极限状态设计表达式及分项系数,并开展了道床板极限状态法试设计,主要结论如下。
(1)建议在客货共线铁路弹性支承块式无砟轨道结构设计时,采用考虑支承块、块下垫板、橡胶套靴的计算模型,加载方式采用最不利加载形式。
(2)对于距洞口小于200 m地段隧道内弹性支承块式无砟轨道道床板,建议承载能力极限状态下,列车荷载和温度梯度作用分项系数分别取1.2、0.5,正常使用极限状态下分别取0.7、0.5。
(3)采用极限状态法对弹性支承块无砟轨道结构道床板进行了配筋计算,距离洞口小于200 m地段道床板纵向配筋结果与容许应力法计算配筋一致;横向上表面和下表面配筋分别减少2φ16 mm和6φ16 mm。

