挡土墙地震主动土压力拟静力法的集中与分散模式对比

郑 涛,肖世国

(1.西南交通大学地质工程系,成都 610031； 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

引言

挡土墙是边坡工程中广泛应用的支挡结构，土压力是作用在挡土墙上的主要荷载，在地震作用下的土压力是挡土墙抗震设计的重要因素之一。因此，合理简便地确定地震土压力是挡土墙抗震设计实践中所关注的重要问题之一。

地震土压力的经典计算方法之一是Mononobe-Okabe法(简称M-O法)，该法基于库伦土压力理论，采用拟静力方式将地震作用转化为地震惯性力，作用于滑动土楔体。由于受制于库伦土压力的假定条件，M-O法也存在不适于黏性土、无法确定土压力分布模式等局限性。SHUKLA等[1]分析了复杂条件下黏性土地震土压力，拓展了M-O法的应用范围。M-O法假定地震土压力线性分布，土压力作用点位于距墙底1/3墙高处，而大量试验发现，地震主动土压力合力大小与M-O法结果接近，但地震土压力作用点高于1/3墙高[2-6]。实际上，基于M-O法基本假设，条分法可确定土压力分布问题。刘忠玉[7]采用水平层分析法得到了无黏性土地震主动土压力非线性分布；王立强等[8]推导了加速度均匀和线性分布情况下无黏性土地震土压力非线性分布模式，得到土压力作用点在0.42～0.46倍墙高之间；林宇亮，孙勇等[9-12]分别利用水平条分和斜向条分的方式推导了考虑填土坡顶倾斜、填土黏聚力、墙土黏聚力、坡顶受均布荷载、拉裂缝存在等复杂条件下地震主动土压力计算公式；夏唐代等[13]考虑地震加速度放大效应，结合拟动力法和水平层分析法，得到考虑时间和相位变化时挡土墙后黏性土地震主动土压力非线性解；张国祥[14-15]在水平层分析法基础上，通过旋转挡土墙模型的方式对拟静力条件下土压力问题进行转换，简化了地震土压力计算公式推导过程；HAN等[16]采用水平条分方式给出了层状填土地震土压力的拟静力计算方法；陈奕柏[17]用斜向条分方式推导了考虑挡土墙偏转影响的地震土压力分布、合力及其作用点位置计算公式。

以往这些采用水平或斜向条分方式计算地震土压力的方法，得到了一些有意义的结果。然而，需注意的是，在基于条分模式采用拟静力法分析地震土压力时，地震惯性力存在两种可能的施加方式，一种是针对各土条将地震惯性力施加于该土条质心，简称“分散模式”；另一种是将滑动土楔体视为整体，地震惯性力施加整个滑体的质心，简称“集中模式”。现行规范[18]中也说明了有这两种施加地震惯性力的方法，但并未指明这两种模式的差异性及其工程适宜性。

鉴于此，针对墙背倾斜、层状填土、顶面有局部条形荷载等一般条件下的刚性挡土墙地震主动土压力问题，基于拟静力算法，采用斜向条分法研究“分散模式”与“集中模式”施加地震惯性力时，其对地震主动土压力大小、分布形式、作用点位置及挡土墙稳定性分析结果的影响或差异。

1 地震主动土压力算法

1.1 公式推导

为简化分析，对挡土墙和墙后土体作以下基本假设：

(1)挡土墙为刚性体；

(2)墙后土体为层状土体，各层土面均为平面且平行于整个土体顶面；

(3)墙后土体达到极限平衡状态时，破裂面是一个过墙踵的平面。

针对墙后滑动土楔体，采用平行于墙后土体顶面的斜向条分法(自上而下分为n个等厚平行土条)分析土压力问题(图1)。其中，假定各土条的上下表面切向力相互抵消[19]，即，条间切向力对墙背土压力的影响很小[20]，可忽略不计，以近似简化分析问题。

对于地震惯性力施加的分散模式，第i条块受力模式如图2所示。在图1、图2中，H为墙高；β为填土顶面倾角；α为墙背竖向倾角；θ为土体破裂角；R和N为破裂面下土体对滑动土楔体的法向力和切向力；P和T为墙体对滑动土楔体的法向力和切向力；Ri和Ni为破裂面下土体对条块i的法向力和切向力；Pi和Ti为墙体对条块i的法向力和切向力；Wi为条块i质量；qi为条块i-1与条块i之间的竖向作用力，假定其作用于两者界线的中点(对于第一个土条q1大小和作用点由坡顶面荷载q确定)；cwi、δi、ci、φi分别为第i条块墙土间黏聚力、墙土间摩擦角、填土黏聚力和内摩擦角；kh为水平地震系数；kv为竖直地震系数。填土表面作用距墙顶内缘水平距离为a、分布宽度为b的均布条形荷载q。

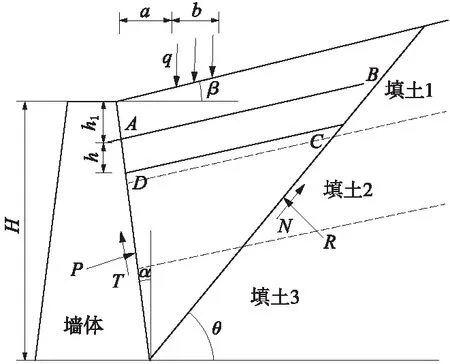
图1 一般条件下刚性挡墙主动土压力分析模型

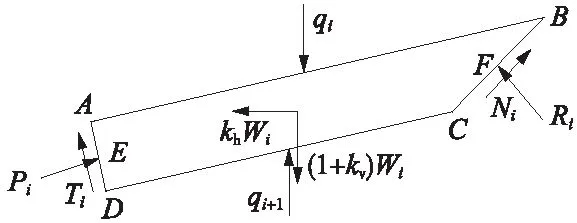
图2 分散模式时任一条块受力示意

由图1、图2中的几何关系可得

(1)

式中，若土条厚度足够小，则可近似认为AB=CD=EF，以简化计算。

对第i土条ABCD建立静力平衡关系，可得

(1)水平向力的平衡方程

Tisinα-Picosα-Nicosθ+Risinθ+khWi=0

(2)

(2)竖向力的平衡方程

(1+kv)Wi+qi-qi+1-Ticosα-Pisinα

-Nisinθ-Ricosθi=0

(3)

(3)对于BC段中点F的力矩平衡方程

[(1+kv)Wi|EF|+qi|AB|-qi+1|CD|]cosβ/2-

[Ticos(β-α)-Pisin(β-α)]|EF|-

khWi|EF|sinβ/2=0

(4)

由于墙后滑楔体处于极限平衡状态，根据Mohr-Coulomb强度准则，Ni和Ti满足

Ti=Pitanδi+cwi|AD|

(5)

Ni=Ritanφi+ci|BC|

(6)

将式(5)、式(6)代入式(2)～式(4)，于是，式(2)～式(4)中所包含的4个独立未知量Pi、qi+1、Ri与θ，可通过这3个方程得到Pi、qi+1、Ri分别与θ的关系式。这样，由i=1(第1条)开始，可计算得P1、q2、R1分别与θ的关系式，将其代入第2条的平衡方程中，便可算得P2、q3、R2分别与θ的关系式，由此依次向下递推到第n条(最后一条)，可得到每一条块相应的土压力与θ的关系式。从而，将每个条块相应墙背的法向土压力Pi与切向力Ti分别叠加，可得到整个墙背法向土压力和切向力的合力En、Tn(均只含一个未知量θ)，即

(7)

最后，整个墙背主动土压力合力Ea为

(8)

对于地震惯性力施加的集中模式，非滑体质心及滑体质心所在条块土条受力模式分别如图3(a)、图3(b)所示，其中，W为整个滑动土楔体的重力。

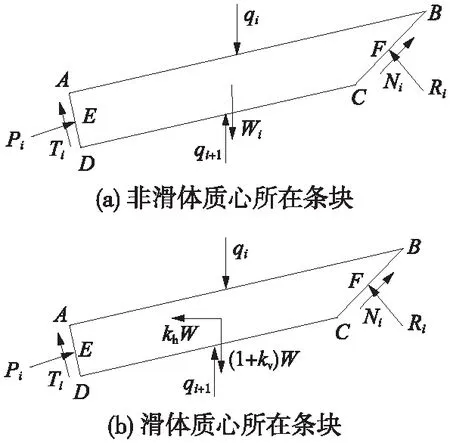
图3 集中模式时任一条块受力示意

对非质心所在条块，其静力平衡关系为

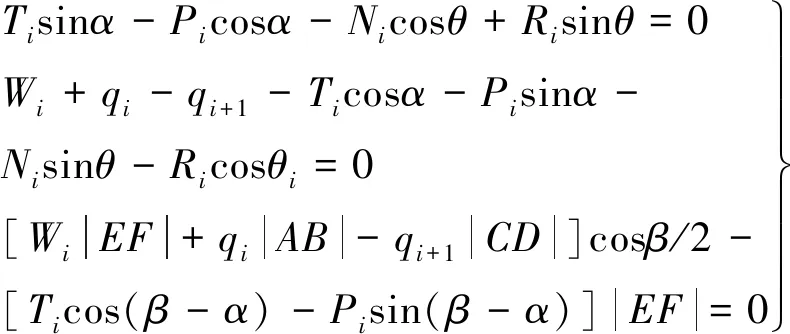
(9)

对质心所在条块，其静力平衡关系为

(10)

于是，根据式(9)、式(10)，同样采用前述方法，通过式(5)～式(8)，可求解出集中模式的主动土压力合力(只含一个未知量θ)。

1.2 计算求解

由前述可见，由式(8)确定的主动土压力是滑裂面倾角θ的函数，根据主动土压力概念，Ea是θ变化过程中(0<θ≤90°+α)相应的土压力极大值，即有

(11)

因此，根据式(11)可确定墙后土体处于主动极限状态时滑裂面倾角，再由式(8)即可确定相应的主动土压力。

2 实例分析与验证

某铁路工程重力式路肩挡土墙，墙体为混凝土，路基填料属于砂类土，墙体置于工程性质良好的地基上。墙高9.6 m，其余尺寸见图4。墙体及土体主要物理力学参数见表1。设计水平地震系数kh=0.1，竖向地震系数kv=0。

图4 实例横断面(单位：m)

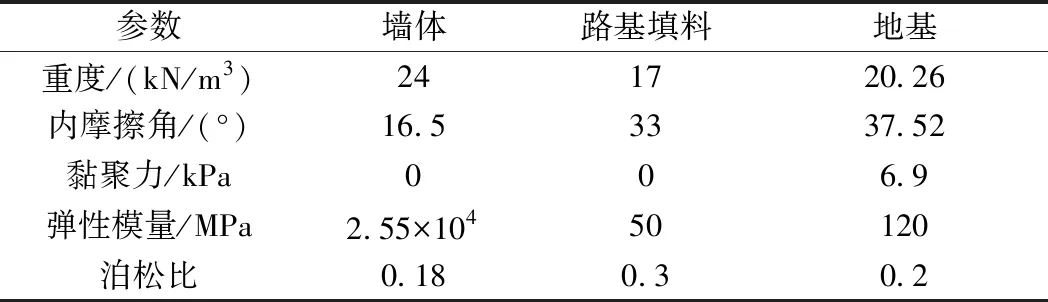
表1 实例主要物理力学参数

分散与集中模式下地震主动土压力计算结果见表2。表中同时给出了FLAC3D数值模拟(模型见图5)与振动台模型试验(与表1参数具有相似性)结果。可见，对于本例，分散与集中模式得到的地震主动土压力大小相同，比振动台模型试验结果偏高约6.6%，FLAC3D比试验结果偏高5.3%，各方法土压力值较为一致。对于土压力合力作用点位置(以土压力作用点距墙底高度与墙高之比定义为作用点高度比)，分散模式与模型试验、FLAC3D结果均较为接近，明显低于集中模式的结果，后者位置比前者高出33%(表2)，说明相对于分散模式，集中模式时墙体稳定性更不利。此外，集中模式时土压力分布图中明显存在一个应力集中点(图6)。

表2 各方法得到的土压力结果

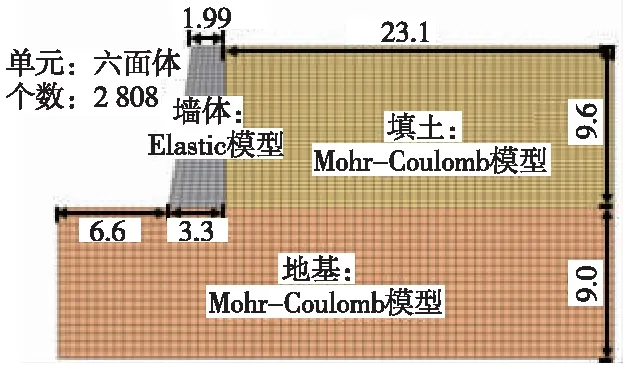
图5 实例FLAC3D数值模型(单位：m)

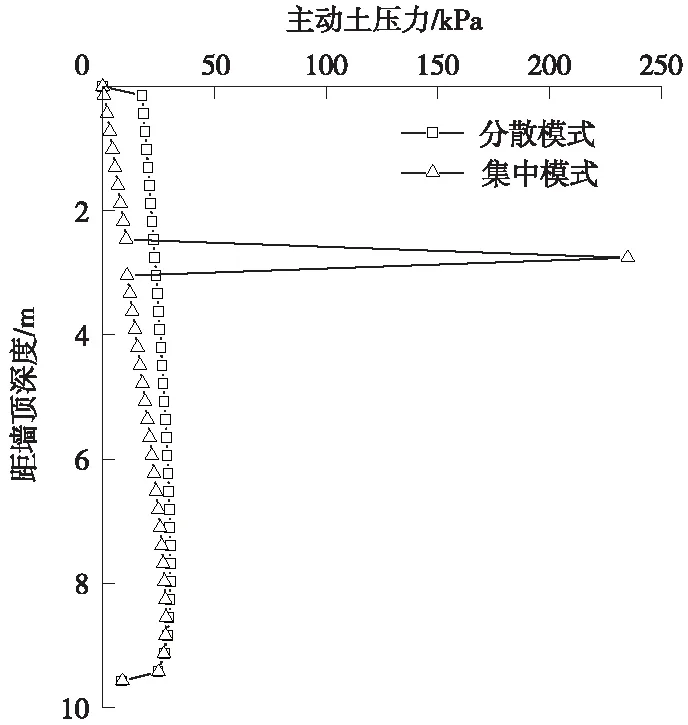
图6 分散与集中模式地震主动土压力分布

3 集中与分散模式差异性分析

3.1 主动土压力大小

(1)实例1——墙后均质填土

某重力式挡墙墙高H=5 m，α=5°，β=10°；墙后土体重度γ=19 kN/m3、黏聚力c=5 kPa、内摩擦角φ=30°；墙-土界面δ=0.5φ，cw=0.5c；设计水平地震系数kh=0.2、竖向地震系数kv=0.5kh；在土体表面作用的局部条形荷载q=10 kPa，相应的a=2 m、b=1 m。

以上述参数作为基本参数，采用控制变量法，按照本文方法得到分散模式与集中模式下地震主动土压力随土体顶面倾角、墙背竖向倾角以及土体内摩擦角、黏聚力变化曲线如图7所示。可见，在各种参数变化下，对于本例所示的均质填土，两种模式得到的地震主动土压力大小相同。

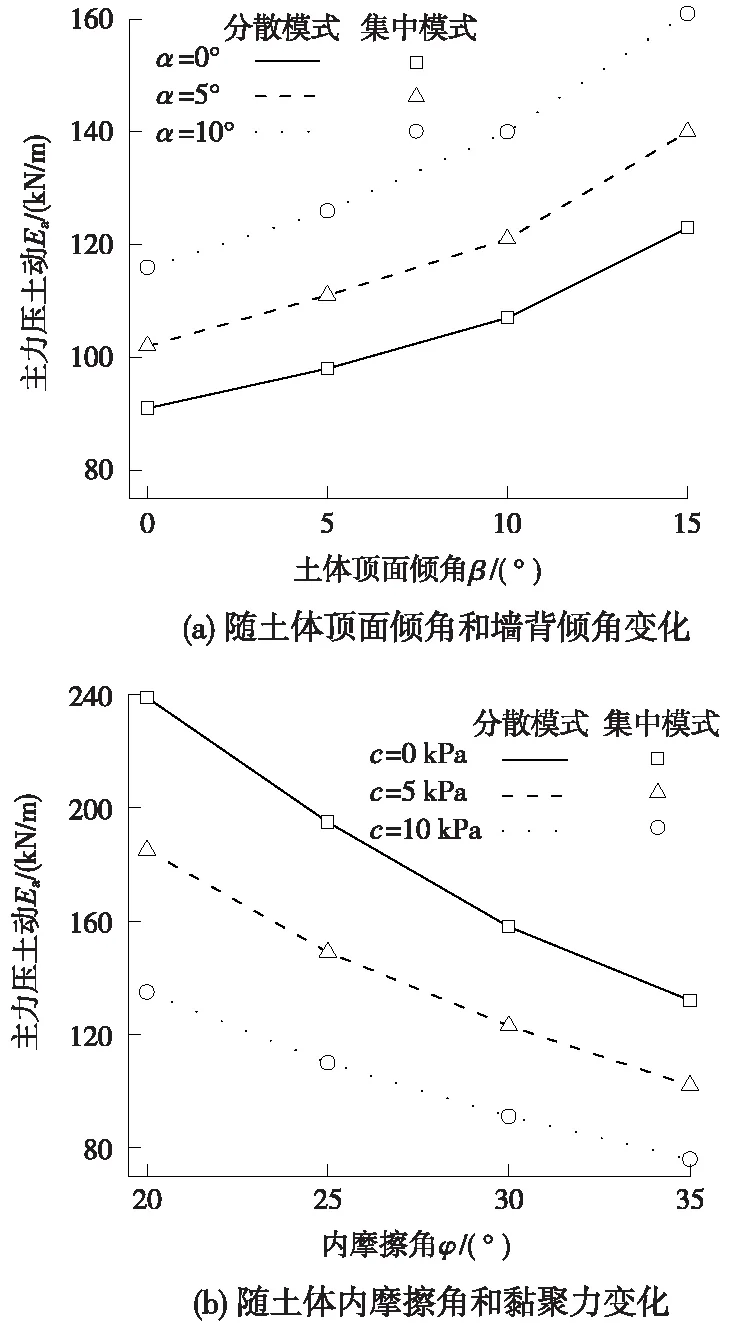
图7 实例1两模式的地震主动土压力对比

(2)实例2——墙后两层不同性质填土

如图8所示的某墙背直立的刚性挡墙墙高H=6 m，墙后填土水平，表面有大小为10 kPa的满布荷载，填土为两层性质不同的土体，每层厚3 m，具体参数见图8，其余参数同实例1。在不同水平地震系数下，分散模式与集中模式得到的地震主动土压力结果如图9所示。可见，对于本例所示的两层填土，两种模式得到的地震主动土压力大小相同。

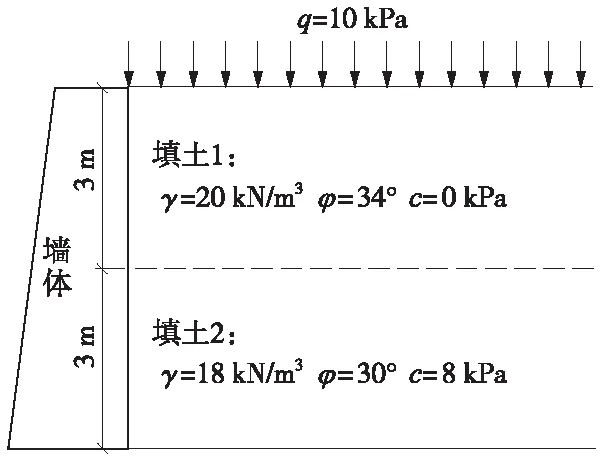
图8 实例2

图9 实例2两模式的地震主动土压力对比

(3)实例3——墙后三层不同性质填土

如图10所示的某俯斜式刚性挡墙墙高H=9 m，填土表面水平且无荷载。墙后填土为三层性质不同的土体，每层厚度为3 m，具体参数见图10，其余参数同实例1。在不同水平地震系数下，分散模式与集中模式得到的地震主动土压力结果如图11所示。可见，对于本例所示的三层填土，两种模式得到的地震主动土压力大小相同。

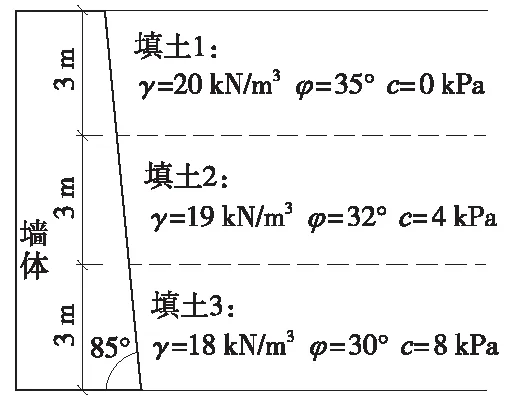
图10 实例3

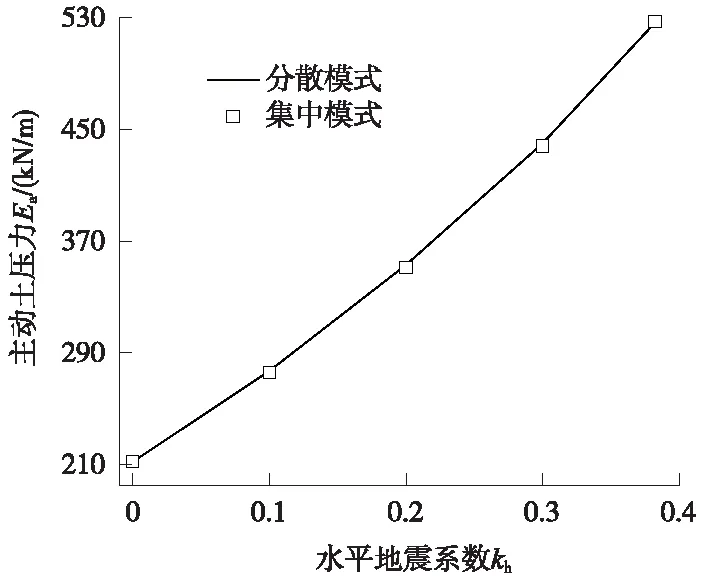
图11 实例3两模式的地震主动土压力对比

3.2 主动土压力合力作用点

对于前述工程实例1、2、3，分散与集中模式时地震主动土压力合力的作用点位置比随水平地震系数变化曲线如图12所示。可见，两种模式下土压力作用点位置比均随kh增大而增大，当kh>0.2后，集中模式的结果趋于收敛，但分散模式的结果仍显著增大，呈近似线性变化；kh<0.4时，分散模式的土压力作用点位置比均小于集中模式，在kh=0.2时，两模式地震土压力作用点位置比差值达到最大值，其后差异逐渐减小。因此，就墙体抗倾稳定系数而言，集中模式比分散模式计算值偏小，偏于安全一面，尤其当kh<0.2时其差异较为明显。

特别地，对于分散模式，以实例1为例，其土压力分布随水平地震系数变化结果如图12所示。可见，由于滑动土楔体呈倒三角形，此时土楔体上部土条的地震力比下部土条大，因而，随水平地震系数增大，上部土条的土压力也相对显著增大，导致整个土楔体的土压力作用点位置逐渐升高，如图13所示。

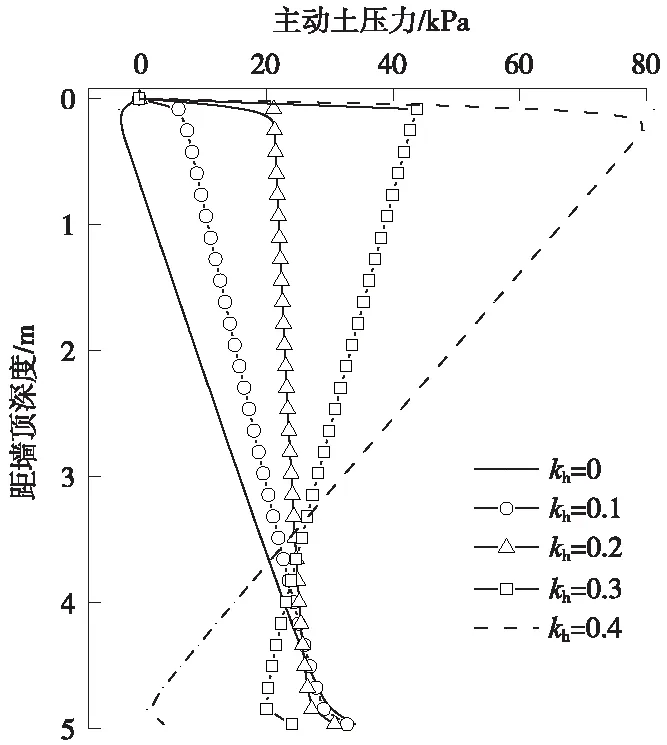
图12 实例1分散模式土压力分布

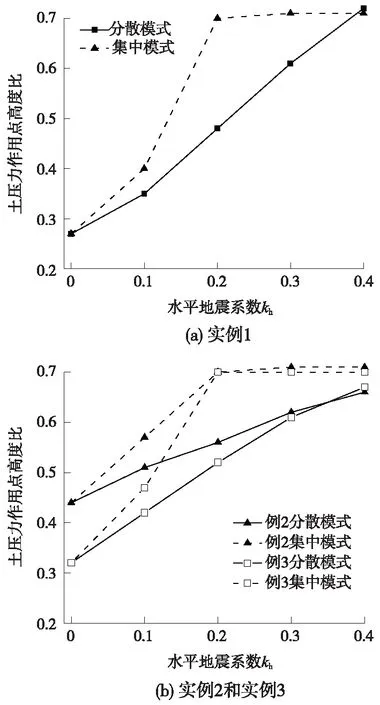
图13 两模式的土压力作用点位置比对比

为进一步说明此问题，针对实例1，以图14所示的某混凝土挡墙设计方案给出具体结果，其中，墙体重度γw=23 kN/m3，挡墙与地基摩擦系数取0.4，由规范[21]规定的地基承载力抗震调整系数，可取地震条件下地基抗震容许承载力[σ]=325 kPa，且根据规范[22]定义地基承载稳定系数为[σ]/σmax(σmax为墙底最大压应力)。在不同水平地震系数下，墙体及地基承载稳定系数计算结果见表3。

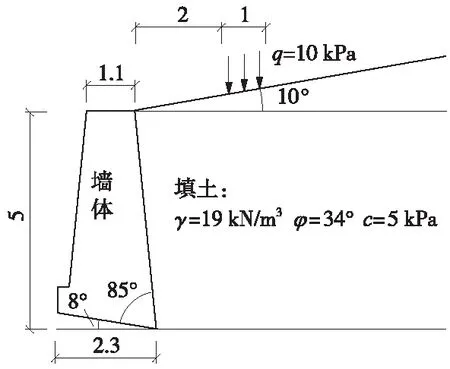
图14 某混凝土挡墙设计方案(单位：m)

表3 两模式的墙体及地基承载稳定系数对比

由表3可见，在不同设计地震水平系数下(kv=0.5kh)，两种模式的墙体抗滑稳定系数相同；对于墙体抗倾稳定系数，在kh<0.4时，分散模式大于集中模式，二者相对差值(以分散模式为基准)变化曲线如图15所示，相对差值随着kh增大呈先增后减趋势，在kh=0.2时，两模式的墙体抗倾覆稳定系数差值达到最大。类似地，对于地基承载稳定系数，分散模式的结果亦大于集中模式(在抗倾稳定系数小于1时，墙体倾覆而无基底压应力)。因此，综合而言，对于墙体稳定性及地基承载力，集中模式比分散模式的计算结果均偏于安全一面。

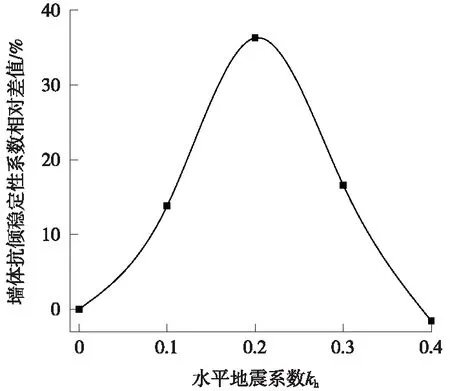
图15 两模式的墙体抗倾覆稳定系数差异

就本设计方案而言，若取kh=0.2(kv=0.1)，则集中模式抗倾覆与地基承载稳定系数均不满足规范要求[19]，因而，需调整墙体的设计几何尺寸，取墙顶宽为1.4 m、墙底宽为2.9 m，其墙体抗倾覆稳定系数可达1.46(大于1.3)，地基承载稳定系数达到1.02，满足墙体地震稳定性要求。因此，相比于分散模式，集中模式所设计的每延米墙体的混凝土方量增加约20.5%。

4 结论

基于拟静力法，采用平行于土面的斜条分方式，对地震惯性力施加的分散模式与集中模式，推导了地震主动土压力计算公式，对比分析了两种模式计算结果的差异，主要得出以下结论。

(1)对于地震主动土压力，可采用斜条分法，基于各土条力的平衡方程，采用递推方法建立墙背主动土压力与土体破裂面倾角之间的关系，从而根据极值求解方法确定土压力及破裂角。

(2)无论墙后是均质填土还是层状填土，对于地震主动土压力，分散模式和集中模式计算的土压力合力大小相同。

(3)分散模式和集中模式计算的地震主动土压力分布模式不同，集中模式时存在显著的土压力应力集中点。

(4)集中模式的地震主动土压力作用点高于分散模式结果，随着水平地震系数由零开始逐渐增大，二者差异先增大后减小，当水平地震系数取0.2时，二者差异最大。

(5)对于墙体稳定性和地基承载力，分散模式大于集中模式的计算结果，后者比前者的设计结果偏于安全一面(相对保守)。