新高考背景下提升高三数学一轮复习效果的几点探索
杨元韡 (江苏省常州高级中学 213003)
随着《普通高中数学课程标准(2017年版2020年修订)》(下称《课程标准》)的颁布,全国大部分省市已陆续进入新高考阶段.从2021年起,江苏等七省的数学高考采用全国新高考I卷,近两年的全国新高考I卷相对于江苏省自主命制的高考卷,在试卷结构、试题题型、试题难度、考查内容上都发生了较明显的变化,最为显著的变化是全国新高考I卷没有考试说明,给命题带来了更大的灵活性.
面对上述变化,高三数学一轮复习起着至关重要的作用.一轮复习不仅要全面梳理知识,更要注重知识之间的联系,纵横比较,揭示规律,提炼方法,构建网络,而且还要为二轮大单元微专题复习提供知识、方法、思想的基础,提升学生在陌生情境中解决问题的能力.如何在新高考背景下提升高三数学一轮复习效果就成为一个值得探讨的话题.笔者根据自身高三数学一轮复习的教学实践,结合苏州大学出版社出版的《高中数学教学与测试(总复习)》(下称《总复习》)等教学资源,谈几点做法.
1 引导学生形成整体观与联系观,构建知识网络体系
通过教师的积极引导,让学生形成整体观与联系观,以构建知识网络体系,是一轮复习的重要任务.这里的整体观主要是单元内的整体观,即立足于单元整体视角,明确单元的逻辑主线,凸显单元的核心内容,厘清单元内各部分之间的关联.这里的联系观是指在融会贯通单元各节、单元之间内容的基础上,形成综合运用单元内或单元间多个知识点与方法解决问题的意识,充分体现了思维的广阔性与灵活性.为增强学生的整体观与联系观,可先从单元入手,合理划分每一节内容,再从节这个更小的单位,引导学生理清它所包含的知识关联,继而将各节知识进行“整合”,构建本单元的知识网络体系,其常见的“整合”形式为制作思维导图或框图.
据笔者广泛了解,大部分高中学校采用一轮复习参考书与校本资料相结合的形式作为一轮复习的资源.市面上多数高三数学一轮复习参考书的知识梳理部分是以填空题的形式罗列本节的知识点,以识记为主,容易造成知识的碎片化.以“三角函数”作为大单元为例,《总复习》将其划分为7节,“三角函数的和、差、倍角公式”是其中一节,该节的“本课导航”栏目中既清晰明了地给出了《课程标准》对本节课的学习要求,还给出了公式关系图(因篇幅所限,仅列部分):
(1)两角差的余弦公式cos(α-β)=cosαcosβ+sinαsinβ(记作Cα-β),可以采用几何证法(麦克肖恩证法)或者向量证法(向量数量积的“算 两次”).
这样的公式关系图不仅给出了具体的公式,还粗略地给出了它们的关联,并没有像教材中那样详细地给出过程,有较大的“留白”空间.事实上,在有意义的条件下,三角函数的和、差、倍角公式都是恒等式,可以通过代换的方法从一个公式得到另一个公式,从而形成一串公式.教师可以让学生补全这些“箭头”推理的“留白”空间,在厘清各公式联系的同时,强化变换这一基本思想,更好地帮助学生作出本节内容或整个单元的思维导图或框图,构建知识网络体系.教学实践表明,一般来说,学生越是善于做单元的思维导图或框图,其数学学业水平往往也越好.
2 例题精选兼顾单一性与综合性,以螺旋式巩固旧知
在高三数学一轮复习中,例题的选择要依据复习的内容而定.例如概念复习课的例题要聚焦概念本身,通过对概念的辨析与运用,让学生厘清概念的内涵与外延;再如公式复习课的例题要关注公式及其各类变形的运用,增强运用公式的灵活性等.
精选例题要兼顾单一性和综合性.例题的单一性是指例题本身考查的知识点或方法单一,其目的更加凸显所要复习的核心概念、定理、公式等,去除一些冗繁的干扰条件,直奔主题;例题的综合性是指例题本身考查的知识点或方法有多个,往往需要综合运用已经复习的知识点、方法及本节知识点、方法才能顺利解决.综合性例题的好处在于对已学习内容进行巩固,同时又将问题的重心放在对本节课内容的考查上,不喧宾夺主.如果高三一轮复习都采用单一性例题线性地推进复习过程,前面学习的内容很容易遗忘;如果都采用综合性例题复习,则时间上消耗过多,且主题不够凸显,容易出现费时费力又效果不佳的窘境.因此,两者要兼顾,它们的比例可以根据学情调整,这样可以以螺旋式巩固旧知,减少遗忘.从近几年的全国I卷来看,综合性的试题占有相当大的比例,单一性的试题越来越少,这是新高考变化的整体趋势.下面给出两例及说明.
·单一性的例题举例(《总复习》第5.1节例2及变式形成的题组):
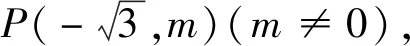
变式1 已知角α的终边经过点P(5m, -12m)(m≠0),求sinα,cosα,tanα的值.
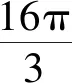
说明此题组聚焦三角函数的定义,三个问题的难度拾阶而上.例题与变式1都是利用终边上点的坐标来求相应的三角函数,其中包含方程思想、分类讨论思想,属于定义的正向应用;变式2可以通过挖掘情境中的信息,利用三角函数的定义得出点坐标,属于定义的反向应用.通过对题组的思考,学生对三角函数的定义会有较为深刻的认识.
·综合性的例题举例(《总复习》第5.5节 习题):
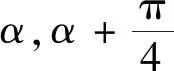
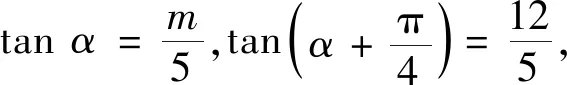
说明本题小巧精致,虽为习题,但仍可作例题使用.一方面考查了三角函数的定义,另一方面考查了三角函数和差角公式,但是考查的重心仍在后者,起到了复习旧知又巩固新知的效果.本题可以利用正余弦的和差角公式求解,也可以用正切的和差角公式求解,具有较宽的入口,不禁锢学生思维,教师可以让学生比较多种解法哪个更简洁.
3 习题选择注重层次性与创新性,增强学生思辨能力
在高三数学一轮复习中,习题选择是非常重要的,它是提高学生学习质量的重要途径.习题选择建议以备课组为单位,进行合理分工,保质保量完成整体的习题设计,减少每位教师工作量的同时提高效益.
习题选择要注重层次性,要有基础题、中档题、较难题及难题,它们的比例可依据学情而定.基础题应聚焦概念、定理及公式本身;中档题与较难题有一定的思维量,不偏不倚,需要综合运用多个知识和方法解决;难题往往具有较高的思维量,有一定的探究性和启发性.这样可以让学生从多个难度层次上得到练习.《总复习》将习题按难度要求分为三类:练习巩固、思考运用、拓展探索,相对而言题量适中,有较大的选择余地.若删除了其中部分习题,不足的部分可以用校本资料作为补充,形成适合本校学生学情的资源库.
习题选择要注重创新性.新高考背景下试题的创新力度非常大,如出现以社会生活、数学文化为背景的情境题,解答题中出现的结构不良试题体现了条件设置的变化,填空题中出现的举例题则体现了设问形式的变化.面对新高考不断创新的特点,习题中也要选择适当的具有创新特色的题目,来增强学生的思辨能力,减少畏惧心理,以便学生从容应对陌生情境.《总复习》紧扣新高考特点,设置了一系列创新性问题,这些问题大部分集中在拓展探索栏目里,非常值得基础中等及以上的学生选用.下面以2022届高三四校联考的一道试题为例,说明其创新之处.
题目已知△ABC中,角A,B,C所对的边分别为a,b,c,sinBcosA>sinC.
(1)求证:B为钝角;
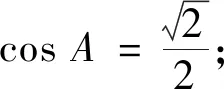
解析(1)证略(提示:可以化“边”证明,也可以化“角”证明).
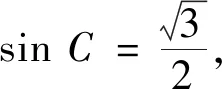
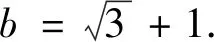
说明本题不属于结构不良题,尽管结果是封闭的,但仍具有探究性.本题的主要亮点是设问方式比较新颖独特,具有创新性的特点.要求证明只有某确定的3个条件组成的条件组存在相应的三角形与之对应,言外之意是含3个条件的其他条件组都不存在相应的三角形与之对应.解答时,如果学生结合(1),很快就得到①②相互矛盾,通过推理发现只有两种可能,这样就减少了讨论的类别,最后判断这两种情形即可.本题考查了学生的逻辑推理能力和思辨能力,是一道非常好的试题,作为习题或考题使用都比较合适.
4 “错题”改编体现变化性与延展性,潜移默化纠正偏差
在高三数学一轮复习中,学生做错题的归因是多样的,有一些是对数学概念、定理、公式的理解出现偏差造成的,也有一些是审题不清、运算错误等造成的.若将学生做错的题简称为“错题”的话,则典型的“错题”往往不是在极个别的学生中出现,而是在一个小群体(约20%~30%的学生)中出现,主要是因为概念记忆模糊不清、对定理与公式的适应条件不清、基本思想方法不熟练等原因造成的.
以典型的“错题”为蓝本,经过改编,可以成为具有变化性和延展性的题组,适合进行有针对性的偏差纠正.改编的方式,可以是转换试题的情境,可以改变试题的设问方式,可以交换条件(或部分条件)与结论(或部分结论),这样改编题在形式上与“错题”有较大差别,学生对它们具有新鲜感.长期做“错题”改编,能达到潜移默化、润物细无声般的纠偏效果.具体的做法流程为“题目→错解→交流→归因→改编→反馈→总结”,其中的交流环节即与做错题目的学生交流找到出现问题的真正原因,它是做好合理归因的前提,“错题”改编之后还有反馈环节,检验学生有没有真正地实现纠偏,最后总结环节应该有一定的延展性,如得到一般性结论,给出方法总结、解题感悟等,避免出现就题论题的情况,最终使学生达到融会贯通的状态.下面以一个数列问题为例,列举部分环节加以说明.
题目已知数列{an}的前n项和为Sn,an≠0,a1=1,且2anan+1=4Sn-3(n∈N*),求数列{an}的通项公式.
错解 因为2anan+1=4Sn-3(n∈N*) ①,所以2an-1an+2=4Sn+1-3 ②.②-①,得2an+1(an+2-an)=4an+1.因为an+1≠0,所以an+2-an=2.因此,数列{an}的奇数项与偶数项构成公差为2的等差数列,故数列{an}是公差为1的等差数列.又a1=1,则an=n.
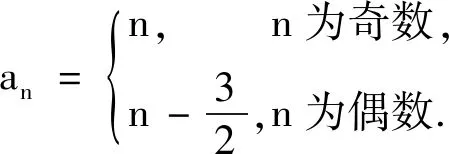
改编(1)一个项数为8的有穷数列{an},其奇数项和偶数项分别构成公差为3的等差数列,但数列{an}不是等差数列,则数列{an}可以是.(写出满足条件的一个数列即可)
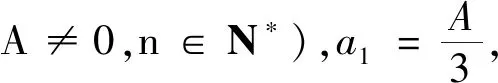
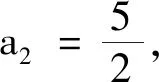
总结(1)若一个数列的奇数项和偶数项分别成公差相同的等差数列,当且仅当该数列的前三项成等差数列时,这个数列成等差数列;(2)先求数列的通项公式,再借助于定义,这也是证明数列是等差数列(或等比数列)的一种方法;(3)回到定义是证明数列是等差数列或等比数列的最根本的方法,深刻理解两个定义非常重要.
5 结语
新高考背景下,如何提高高三数学一轮复习的效果还有很多方面值得我们去思考,本文仅提了几点做法作为探索,希望能抛砖引玉,也希望能看到更多且更有效的在减轻学生学习负担的基础上提高数学关键能力的具体做法!

