着力方法探究 促进思维进阶
——一道中考几何作图题的解法探索与思考
杨牛扣 (江苏省泰州市姜堰区第四中学 225500)
2022年泰州市中考数学第25题第(2)小题是一道尺规作图题,题目虽小,但很精辟,起点低、入口宽,在原有知识基础上考出了新高度.该题融入了多个知识点,蕴含着多种数学思想方法,要求学生有一定的分析推理、逻辑思维能力,体现了从考查知识到考查能力和素养的转变,可以深挖,扩大教学价值.
1 试题呈现
(2022年江苏省泰州市中考第25题)已知在△ABC中,D为BC边上的一点.
(1)如图1,过点D作DE∥AB交AC边于点E.若AB=5,BD=9,DC=6,求DE的长.

图1 图2 图3
(2)在图2中,用无刻度的直尺和圆规在AC边上作点F,使∠DFA=∠A.(保留作图痕迹,不要求写作法)
(3)如图3,点F在AC边上,连结BF,DF.
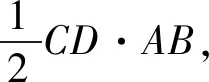
本文主要研究第(2)题尺规作图.
2 新课标视角下的几何作图题解读
2.1 以生为本,递进式构建问题链
本题是试卷的倒数第二题,应该有一定的难度,但该题从学生的角度出发,设置了三个梯度明显的问题,递进式引导学生分步解决,减轻了学生的恐惧心理,提升了信心.第(1)题是起点低的基础题,由DE∥AB,得到△DEC∽△ABC,从而直接可得DE=2;第(2)题尺规作图,有多种解法;第(3)题考查直线与圆的位置关系,需借鉴第(2)题的思路分析,利用面积关系和平行关联出相似,进而进一步求解.所以第(2)题是解决本题的关键,承上启下.第(2)题的基本思路是作一个角等于已知角,平时的画法是先画一条射线,以射线的端点为待定角的顶点,再作出与已知角相等的角.而本题考出了新花样,角的顶点是待确定的点,直接用尺规作图显然难以完成.因此,必须要转移,但怎么转移、依据什么方法转移,是本题思维进阶的精彩之处.
2.2 基于课标,动静中凸显素养观
《义务教育数学课程标准(2022年版)》提高了尺规作图的教学要求:让学生在经历尺规作图的过程中,增强动手能力的同时,更加注重作图原理的探寻、空间观念和逻辑思维的发展.本题以尺规作图为背景,关注方法探究,设置思维生长路径.从第(2)题开始,为学生的思考留白,聚焦初中数学相似、等腰三角形、直角三角形、圆等核心知识,将知识、方法和能力以及数学的素养融为一体,有较好的区分度、信度和效度,要求学生动手画(草图与尺规作图相结合)和动脑想(直观思考与逻辑推理相结合),在数形结合、动(画图)静(思考)交替中凸显数学核心素养的培养.
3 解法赏析
五种基本作图是尺规作图的精华,是解决复杂尺规作图问题的基础[1].面对相对复杂的几何作图问题,找到作图的思路是难点,常用的方法是“画一画、试一试、证一证”,即以结论推条件,先假设已作好,画出草图,然后借助几何直观进行逻辑分析,探索出作图方法,最后通过演绎推理再加以验证.
思路1构造平行和等腰三角形(梯形)转移角.
画法1 如图4,以D为顶点,作∠CDE=∠B,交AC边于点E,则有DE∥AB;再以点D为圆心、DE长为半径画弧,交AC边于点F,进而得到∠DFA=∠A.所以点F即为所求.
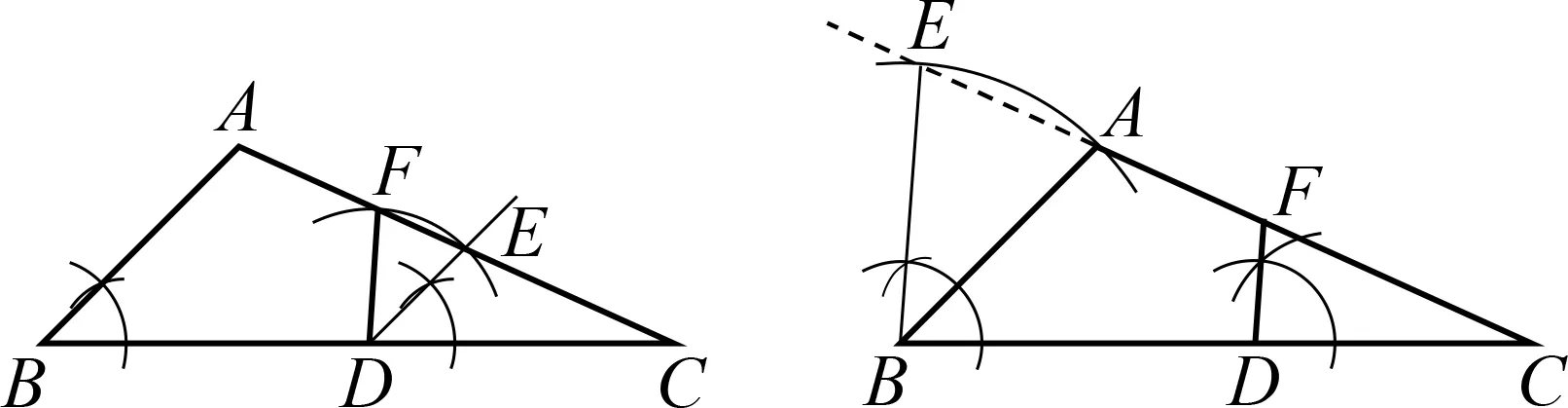
图4 图5
画法2 如图5,以点B为圆心、BA长为半径画弧,交CA的延长线于点E,则有∠BEA=∠BAE;再以D为顶点,作∠CDF=∠EBC,交AC边于点F,则有DF∥BE,进而得到∠DFA=∠BAC.所以点F即为所求.
评析平行线和等腰三角形是几何题中转移角最常见的模型.画法1依据第(1)题顺势而得,是最直接的思路,先依据确定的顶点D,作出一个等角,构造平行的特殊位置关系,将∠A“平行”转移至以E为顶点的角,再利用等腰三角形,将∠A“方向”转移,进而求解.画法2与画法1的思维路径一致,只是转移顺序相反.
画法3 如图6,以点D为顶点,作∠BDE=∠C,交AB边于点E,则有DE∥AC;再以D为顶点,作∠EDF=∠AED,交AC边于点F,进而得到∠DFA=∠A.所以点F即为所求.
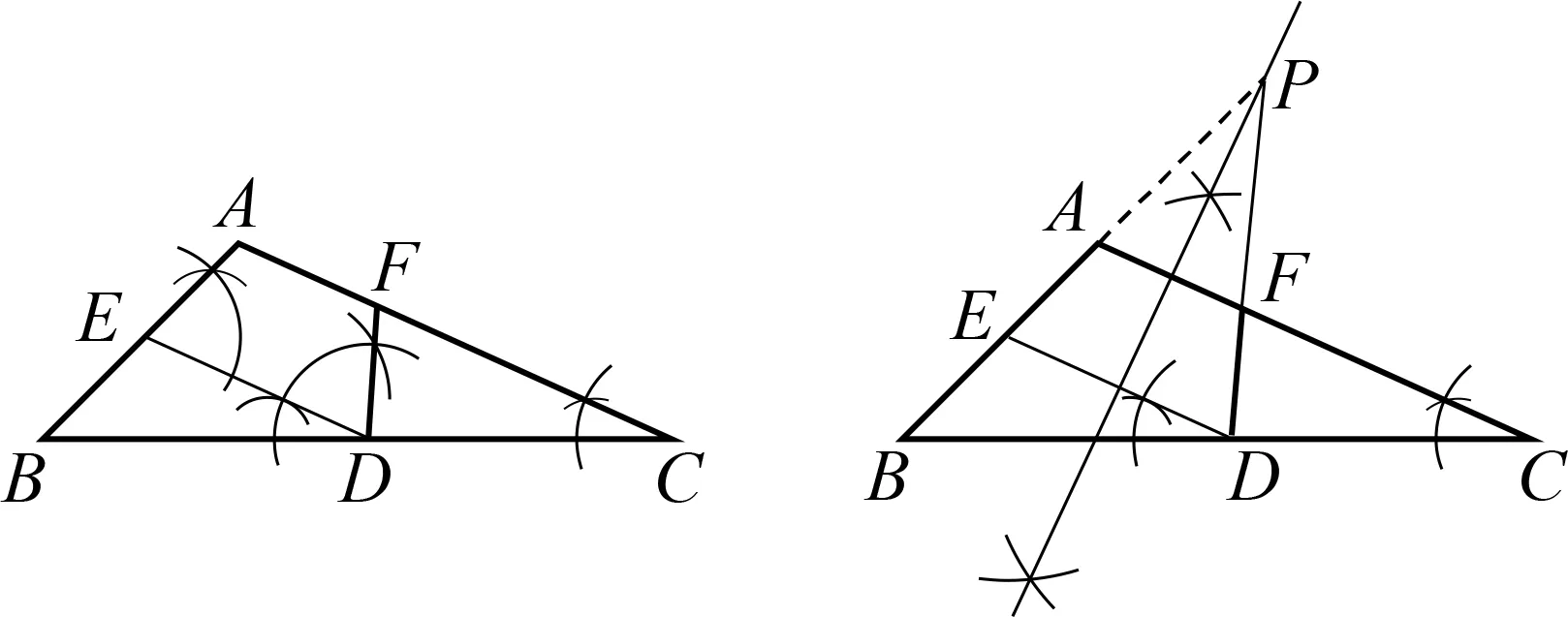
图6 图7
画法4 如图7,以点D为顶点,作∠BDE=∠C,交AB边于点E,则有DE∥AC;再作线段DE的垂直平分线交BA的延长线于点P,连结DP交AC边于点F,进而得到∠DFA=∠BAC.所以点F即为所求.
评析抓住∠DFA=∠A具有公共边的特点,在画法1、2的基础上,转换角度,构造以公共边为一边的对应外角,依据等角的补角相等,自然形成画法3,只不过,此种画法要求学生要对等腰梯形的性质有所了解;若对上述性质不了解,可再利用平行转移角,由相等的角关联到相等的边,从而形成作线段DE中垂线的思路(画法4).
思路2构造相似三角形转移角.
画法5 如图8,以点C为顶点,作∠ACE=∠ACB,交BA的延长线于点E;再以点D为顶点,作∠CDF=∠CEA,交AC边于点F,进而得到∠DFA=∠BAC.所以点F即为所求.
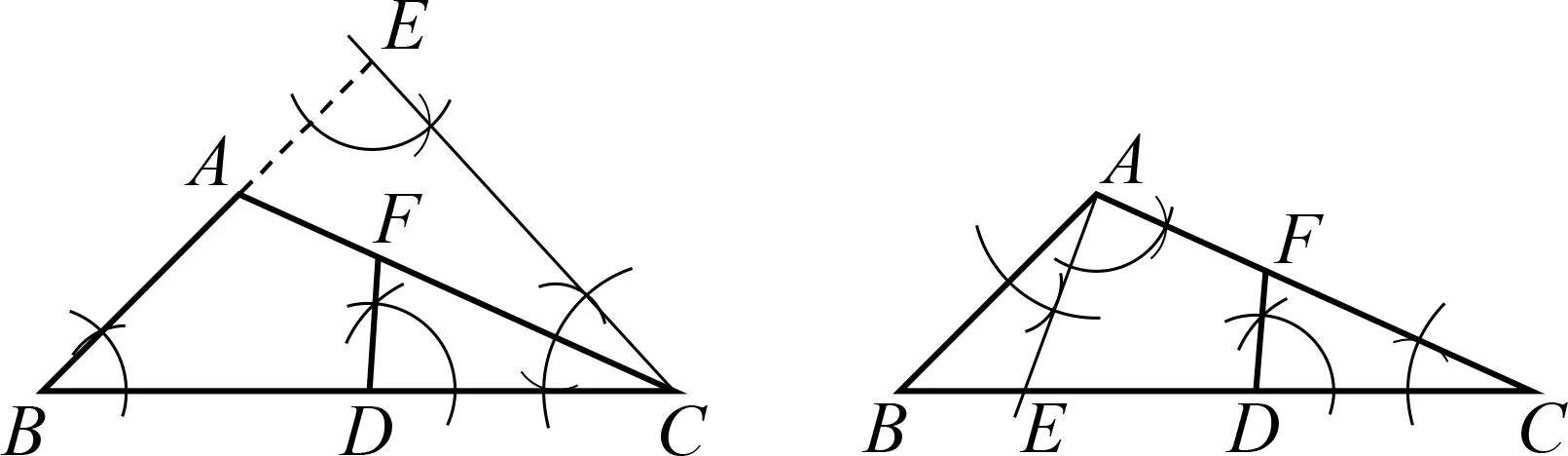
图8 图9
画法6 如图9,以点A为顶点,作∠BAE=∠C,交BC边于点E;再以点D为顶点,作∠CDF=∠CAE,交AC边于点F,进而得到∠DFA=∠BAC.所以点F即为所求.
评析受思路1的启发,继续以寻找相等的角为突破口,不难关联出∠DFA的另一个外角∠DFC,画出草图,由不确定到确定,自然联想到相似三角形的对应角相等.画法5是向外作相等的角,画法6是向内作相等的角,分解∠A.
思路3构造直角三角形转移角.
画法7 如图10,过B,D两点分别作AC边及所在直线的垂线,垂足分别为M,N;再以D为顶点,作∠NDF=∠MBA,交AC边于点F,进而可得∠DFA=∠BAC.所以点F即为所求.
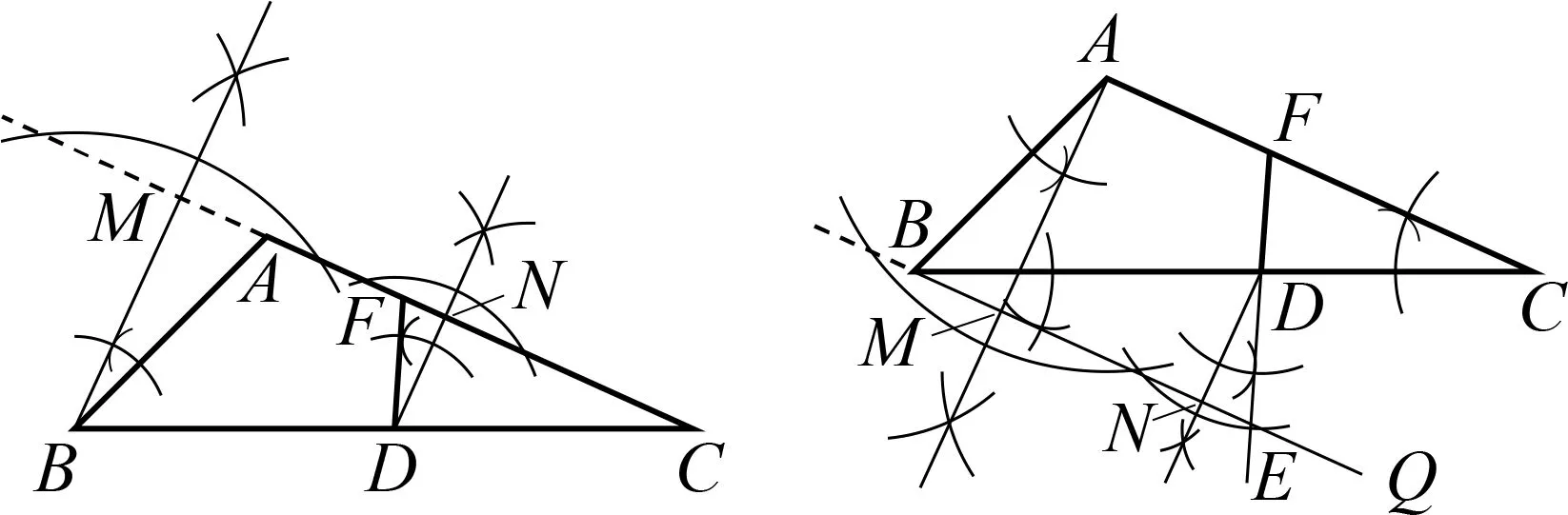
图10 图11
画法8 如图11,以点B为顶点,作∠CBQ=∠C,则有BQ∥AC;分别过A,D两点作射线BQ的垂线,垂足分别为M,N;再过点D作∠NDE=∠BAM,交BQ于点E,延长ED交AC于点F,进而可得∠DFA=∠BAC.所以点F即为所求.
评析依据最近发展区理论,在思路2相似三角形转移角的思路启发下,可以多点开花,构造特殊三角形(直角三角形)转移角.画法8只是极少部分学生的画法,其实质是画法7的延伸,换了一个作垂直的方式,但体现了灵活的思路和扎实的基本功,以及良好的解题素养.
4 教学导向
4.1 关注新课标,正确引导几何作图的教与学
新课标的新要求是我们教学的内容和方向.细化到平时的尺规作图教学中,既要夯实基础,强调五种基本作图的画法,更要注重基本图形和几何直观的重要性,引导学生探索作图的方法,培养学生的探索性思维(包括直接思维、发散思维、联想思维)和直观想象力、逻辑推理能力[2].
本题的精彩之处在于一环套一环,先由基础的相似求线段长,再以作一个角等于已知角的基本作图为切入点,最后关联应用.尽管第(3)问有些难度,但整个题目的灵魂在第(2)问,借助于尺规作图,要求学生利用几何知识加以解决,这是教学中引导学生探究几何作图的常用路径.
4.2 聚焦生长性,深入探究尺规作图的本质特征
如何确定点F是本题的突破点,如果只是简单地从尺规作图的角度去思考,就会很难找.解决尺规作图问题的基本思路是“倒过来想”,面对“∠DFA=∠A”的原始问题,先假设这一点已存在,然后画草图分析,用几何的知识分析推理;有了思路,再细化分解成若干基本作图.这就要求学生能跳出尺规作图看尺规作图,不能仅单纯地记住尺规作图的画法,要善于寻找条件知识与结论知识之间的逻辑关系或转化轨迹[3].这样的思考体现了数学解题过程与结果的统一,其实质就是彰显了数学教学的生长性.学生通过画草图分析推理,在画中思、在思中画,实现“怎么想”“怎么想得到”层层递进的深入思考,形成数学思维的生长链,在几何作图中享受数学思维生长的全过程,这一过程正是新课标下尺规作图本质特征的体现.
“教育的本质就是一棵树摇动另一棵树,一朵云推动另一朵云,一个灵魂召唤另一个灵魂.”平时的教学中,我们要注重提炼几何图形的特征,引导学生追根溯源,关注知识链生成,积极探索作图方法,尝试一题多解、一题多图,让学生在动手实践和推理分析中积累经验,生长思维.

