助力探究 揭示本质
——“用二分法求方程的近似解”教学实录与反思
张国良 (江苏省武进高级中学 213149)
1 基本情况
1.1 授课对象
高一学生已初步理解了函数图象与方程解之间的关系,具备用数形结合解决数学问题的能力,这为理解函数零点附近的函数值符号提供了知识储备.虽然学生熟悉一元二次方程解与函数零点的关系,但对于一元高次方程、超越方程与对应函数零点之间的联系还比较模糊.另外,学生对计算器的使用不够熟练,这些都给学生学习本节内容造成一定困难.
1.2 教材分析
本节课是《普通高中教科书·数学》(苏教版)必修第一册第8章“8.1二分法求方程近似解”第2课时,要求学生能够借助计算器或计算机用二分法求方程的近似解,从中体会函数与方程之间的联系.用二分法求方程的近似解既是本册书中的内容,又是对函数知识的拓展,既体现了函数在解方程中的重要应用,同时又渗透函数与方程、数形结合、转化与化归的数学思想,培养学生的图形能力、判断能力以及利用现代信息技术解决问题的能力.
教学目标 (1)能够借助计算器用二分法求方程的近似解,了解二分法是求方程近似解的常用方法;(2)掌握用二分法求方程近似解的操作流程,感受信息技术的优越性;(3)通过探究活动,体会数学的“逼近”思想,感受精确与近似的相对统一.
教学重点 利用二分法求方程的近似解.
教学难点 二分法求方程近似解的操作流程.
2 教学过程
2.1 情境体验,感受思想
师:同学们,让我们先做一个猜数游戏.
计算机随机给定10~90之间的二位整数,让学生猜这个数,对于每次猜测的结果,计算机的提示是“对了”或“大了”或“小了”(图1).

图1
2.2 师生讨论,理解感悟
师:只要给出一个不超出该范围的整数,采用正确的方法,都可以在7次以内猜中,你们是否可以做到?
师:为什么采用正确的方法,7次以内一定能猜中?
学生讨论并回答.
师:上述猜数游戏中,每次猜数都将所给区间一分为二,进行比较后得到新的区间,再一分为二,进而使得所猜数逐步逼近计算机给出的数,这种思想就是二分法.
师:在游戏活动中我们也能学到很多知识,下面请同学们再举例说明二分法的一些应用.
生:输电线路的故障检测等.
师:我们今天就来一起研究用二分法求方程的近似解.
揭题 用二分法求方程的近似解.
师:前面我们已经学习了一元二次方程实数解的有关问题,如方程x2+3x-1=0有两个不相等的实数解,那么你能知道方程x3+3x-1=0的实数解的情况吗?近似解呢?
2.3 活动探究,课堂建构
师:请同学们对这个三次方程的实数解提出一些问题.
生1:该方程有无实数解?
生2:该方程若有实数解,有几个?
生3:这个实数解大概是多少?
生4:函数y=x3+3x-1的图象是怎么样的?
生5:如何获得方程x3+3x-1=0的近似解?
……
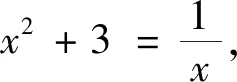
引导学生思考:还可以通过函数的单调性知道该方程只有一个实数解.
师:这个实数解在区间(0,1)内,能否更精确些?
记f(x)=x3+3x-1,设方程x3+3x-1=0的实数解为x0,则x0∈(0,1).
第一次:f(0)<0,f(0.5)>0
第二次:f(0.25)<0,f(0.5)>0
第三次:f(0.25)<0,f(0.375)>0
第四次:f(0.312 5)<0,f(0.375)>0
第五次:f(0.312 5)<0,f(0.343 75)>0
第六次:f(0.312 5)<0,f(0.328 125)>0
第七次:f(0.320 312 5)<0,f(0.328 125)>0
第八次:f(0.320 312 5)<0,f(0.324 218 75)>0
让学生展示自己的解决策略,师生共同完成前三次的计算,组织同桌的两位学生合作,一人计算,一人记录,完成后面的计算过程,并展示学 生的成果.在此过程中教师借助几何画板显示这个实数解的范围逐步缩小,直观形象地体现出二分法的思想(图2).通过这种活动来创造探究 机会,促进学生主动探究,并注重学生参与、探究的实效,在提出问题、建构数学、解决问题方面进行有意识的引导,培养学生的合作精神与协作能力.
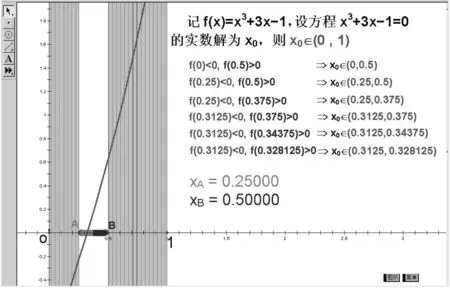
图2
师:若精确到0.1呢?算几次就可以了?
师:若精确到0.01呢?
由学生讨论并总结得出:欲近似到0.1,由两个端点近似值都为0.3,则x0=0.3;欲近似到0.01,由两个端点近似值都为0.32,则x0=0.32.
通过上述解题过程,结合几何画板,形象地给出一段区间,不断地取一半,并表明每一段的两个端点的符号.
师生讨论:(1)精确度如何达到?二分的次数如何确定?有无规律?(2)使用二分法有无前提条件?(3)二分法的一般思路和操作流程是什么?
2.4 巩固反馈,总结提炼
利用计算器,求方程lgx=3-x的一个近似解.(精确到0.1)
小组合作,一人计算,一人记录,完成后通过投影展示学生的研究成果.
通过学生思考并用自己的语言把二分法的解题过程表达出来,并展示学生的成果,让学生共同评价和完善补充.
生:二分法求方程的近似解就是每次都取区间的中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法,其实质是不断把函数零点所在的区间逐步缩小,使区间两个端点逐步逼近零点,进而得到函数零点近似值.
师:大家一起来完善用二分法求方程的近似解的操作流程.
用二分法求方程的近似解的操作流程如图3所示.
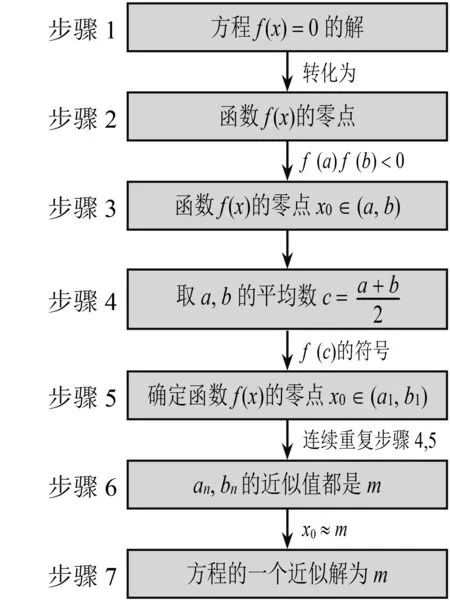
图3
2.5 体验交流,练习拓展
请学生谈谈利用二分法求方程近似解的一些体验,并进行交流.例如:
(1)近似计算高中阶段较少遇到,用二分法求方程的近似解是数学严谨而科学的体现.
(2)无限逼近的思想是高中数学重要的思想方法,如我国古代数学家刘徽用割圆术计算圆周率π也正是用无限逼近的思想.
(3)操作流程是一种算法思想.算法是数学及其应用的重要组成部分,是计算科学的重要基础,通过本堂课让学生感受到程序化思想,体会算法思想在解决问题和培养理性思维中的意义和作用.算法思想已经成为现代人应具备的一种不可或缺的重要数学素养.
师:利用计算器,求方程10x=3-x的一个近似解.(精确到0.1)
师:结合上述方程lgx=3-x,你能得到什么结论?
借助几何画板作图,帮助学生获得y=10x与y=lgx的关于直线y=x的对称关系,从而获得这两个方程的实数解的和为定值3.
·巩固练习
下列函数图象中,不能用二分法求函数零点的是( ).
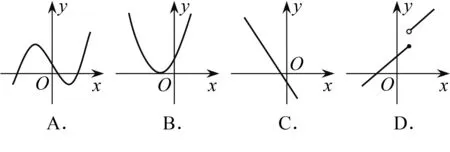
利用以上图象,指出对于连续函数f(x)满足f(a)f(b)<0,则函数在(a,b)上至少有一个零点;但f(a)f(b)>0,却不能得出函数在(a,b)上一定没有零点.
·课后拓展
师:同学们有无其他方法求方程的近似解.
提示:如秦九韶法、迭代法等.
3 回顾反思
3.1 教学效果
利用信息技术与课程整合,动态图象的演示,激发学生学习兴趣、激活学生思维,掌握二分法的本质,较好地完成了教学目标.
3.2 教学反思
本节课通过猜数游戏创设情境,不仅激发了学生的学习兴趣,学生也在猜数过程中初步感受二分法的思想.利用几何画板求方程近似解的动态效果,优势有三:
(1)动态逼近
几何画板能动态展示零点所在的区间,直观地体现“逼近”的过程,动态变化过程清晰明了,这样有利于突破传统教学的难点,帮助学生揭示数学本质,提高了探究活动的有效性,充分体现了信息技术与数学课程的有机整合.
(2)形象直观
在教师的引导下,学生也可以观察图形、猜测并验证,在观察、探索、发现的过程中增强对函数零点的感性认识,形成丰厚的经验背景,从而更有助于理解.
(3)操作简单
借助几何画板可实时作出函数图象,一切操作都只靠工具栏和菜单实现,隐藏、显示可以反复操作.
本节课由学生自主提出一些问题,主动探究,总结体验探究过程,从而获得方法,体验到成功的乐趣.学生只有通过自主探究、创造性运用知识、合作交流才能完成相关课题,这将促进学生学习方式发生转变,由被动接受、死记硬背、机械训练变为自主探究、注重过程、合作交流,有利于提升学生的数学核心素养.

