以史为鉴 循序而为 自然铺路*
姜鸿雁 (江苏省无锡市蠡园中学 214072)
教育哲学家杜威认为,教育即生活,教育即生长,教育即经验的改组或改造.“生长”是世间一切有生命的事物的共同特征[1].如果通过科学地组织教育教学活动,使学生知识的学习、能力的提升、品格的培育如身体那样自然生长,那就实现了“教育即生长”的理想状态.汪晓勤教授提出:数学的学习是知识的逻辑顺序、学生的心理顺序、历史发展的客观顺序的融合[2].笔者在教学实践中,结合具体教学内容,努力遵行“三序融合”的教育教学规律,力争为学生“自然生长”铺路.
1 借史“迎合”心理状态,自然点燃学习知识的火花
《义务教育数学课程标准(2022年版)》提出建议:重视设计合理问题,问题提出应引发学生认知冲突,激发学习动机,促进学生积极探究,让学生经历数学观察、数学思考、数学表达、概括归纳、迁移运用等学习过程[3].课堂教学应充分体现学习新知的必要性,积极营造有利于学生形成“愤”“悱”心理的氛围,激发学习动机,为“启”“发”做准备.在实际教学时,知识的逻辑顺序不一定与学生的学习心理“合拍”,教师应何为?
案例1切线的判定定理.
·教学内容简析
苏科版初中数学教材(下称“教材”)将“切线的判定定理”安排在九年级(上册)第2章第5节第2课时[4].学生经第1课时的学习,知道由直线与圆公共点的个数或d与r的数量关系,可以判断直线与圆的位置关系.从数学逻辑角度,继续学习切线的判定方法是自然的,但从学生角度,切线的判定方法已有两种,为何还要学习切线的判定,仅仅是多一种判定方法?如果只在这个层次,教师“奉送强加”,学生“逆来顺受”,不是理想的“教育即生长”的教学状态.
《几何原本》第3卷命题16对切线的描述:由一个圆的直径的端点作直线与直径成直角,则该直线落在圆外,又在这个平面上且在这直线与圆周之间不能再插入另一条直线[5].“直线与圆周之间不能再插入另一条直线”如此形象直观的表达,适合学生心理,教师可以运用这一史料,设计恰当的问题情境,形成认知冲突,“点燃”想学习新方法的思维火花,为自然学习添砖加瓦.
·部分教学流程及分析
判断下列直线与圆的位置关系(图1~ 图3),并说明理由(实录针对图2和图3).

图1 图2 图3
生1:相切,感觉直线与圆只有一个公共点.
教师将直线延伸(图4).
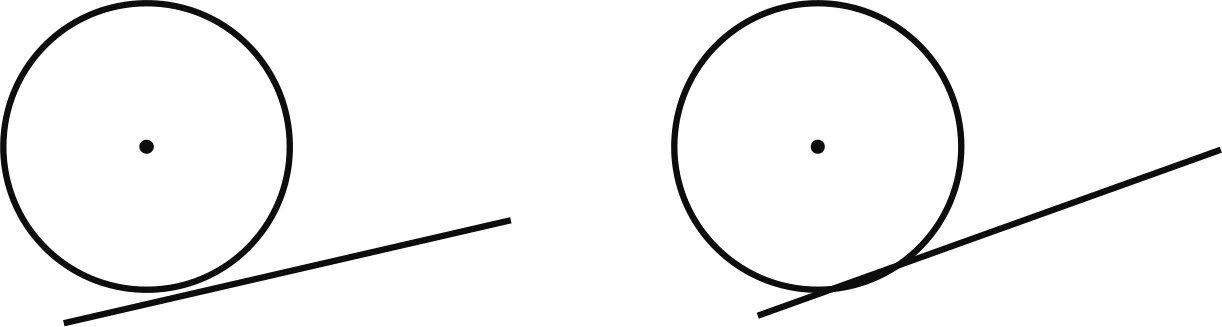
图4 图5
生1:相离,圆和直线之间有一点“空隙”,但像相切.
师:“空隙”说明直线和圆之间还可以“插入”直线.图3呢?(学生提出延伸直线,如图5)
生2:相交,有点像相切,好像只有一个公共点.
师:说说你们此时的想法.
生2:用直线与圆的公共点个数来判断直线与圆的位置关系“不靠谱”.(“不靠谱”好传神!)
生3:可以量圆心到直线的距离d与r,然后比较大小.
生4:度量会有误差,图2和图3的d与r大小一定非常接近,判断不准确.
师:这怎么办呢?已学的两种方法不能很好地解决问题.
生(合):必须要学习其他判定方法!……
评析本设计运用顺应式的方式[6]将《几何原本》第3卷命题16这一史料融入问题情境,设计“判断图2和图3中直线与圆的位置关系”这一问题,产生旧知不能较好地解决问题的现实,学生在直观中尝试→在尝试中质疑→在质疑中修正的过程中点燃思维的“火种”,在“愤”“悱”的心理状态下迈进新知识领域.当笔者将《几何原本》中关于切线的描述展示出来时,学生感叹自己与伟大的数学家想法是相通的,这无疑给学生的学习多了一份积极的心理暗示.
教师根据教学内容,结合历史发展中的相关材料,寻找古今融合点,并整合到教学设计中,促进学生形成认知冲突,有利于点燃思维的导火索,有利于理性思维的自然绽放,有利于良好学习品质的自然形成.
2 由史“深探”逻辑关联,自然指明能力提升的方向
我国现代数学教育家傅仲孙先生提出几何教学的三境界:知其然,知其所以然,知何由以知其所以然.笔者认为,傅先生提出的三境界,不仅对几何教学而且对整个数学教学都有指导性意义.学生在学习过程中,随着基本活动经验的不断积累,有些数学知识的逻辑顺序与学生的心理似乎比较“合拍”,能达到“知其然,知其所以然”的 境界,如果教师在“知何由以知其所以然”下功夫,可以自然提升学生发现问题、提出问题的能力.
案例2求根公式法解一元二次方程.
·教学内容简析

用配方法解关于x的方程ax2+bx+c=0 (a≠0)实现了“知其然、知其所以然”.笔者认为,如何让学生想到用配方法解这个方程是实现“知何由以知其所以然”的关键,没有解决这个问题的学习过程不算自然,知识的逻辑顺序与学生的学习心理顺序“看似合拍”,其实“貌合神离”.教师若能审视历史发展的客观顺序,可以对深度剖析知识内部的逻辑顺序有所启发,使教学设计锦上添花.
·部分教学设计及分析
环节1 思维热身.
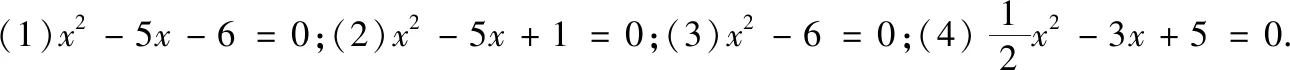
环节2 探索新知.
观察方程(1)~(3)的各项系数与方程的解,发现了什么?(详见文[7])
评析笔者如此设计,是受人类探索一元n次方程求根公式的这段历史的启发.一元二次方程求根公式——看似复杂的“结构”,其独特的对称美反映的是用系数a,b,c表示方程的根,公式就是方程的根与系数之间的“必然关联”,它启发人们继续探索一元三次、四次方程……的求根公式;当人类探索到一元五次方程的求根公式时,数学的王国向人们敞开了另一片天地!可以认为,探究方程的根与系数之间的关联性是这段历史发展的“引擎”,让学生在此得到体悟尤其珍贵!所以笔者通过“控制变量”,分别改变方程的二次项系数、一次项系数、常数项中的一个,设计不同的方程,引导学生发现只要改变方程的一个系数,方程的根随之发生变化,这说明方程的根与系数之间存在着“某种必然关联”,以此激活学生探索新知的心理欲望.只有用字母表示各项系数实现一般化,才能揭示“必然关联”,用配方法解关于x的方程ax2+bx+c=0(a≠0)水到渠成!整个过程不仅巩固配方法、提升运算能力、为下节课作铺垫,更是充分调动学生由已知探究未知的心理需求,自然提升学生发现问题、提出问题的能力.课堂上,笔者用附加式的方式[6]介绍人类探索一元n次方程求根公式的历程,让学生懂得什么是学海无涯.
客观的历史发展顺序可以促进教师深度剖析知识的逻辑顺序,从而促进学生在自然状态下提升能力.
3 展示历史发展画卷,自然提供培育品质的土壤
有些数学核心知识因自身特点,教材编写的专家结合学生的年龄、心理特点,在不同学段,以不同的方式和要求不断渗透,可谓“草蛇灰线,伏脉千里”,实现学生能力发展的阶段性和一致性.学习这些知识时,学生的心理顺序与数学的逻辑顺序融合得一般较好,这为学生自然地学习提供便利,但对教师的教学设计提出新的挑战,如何追求自然生长新的意义与价值?
案例3三角形内角和定理.
·教学内容简析
本节内容教材安排在七年级(下册)第12章第2节第3课时[8].因小学有过实验几何的操作经历,教材第7章已有理性证明的渗透(有些教师已经给予定理证明的教学),学生对这一结论已熟悉于心.如果这节课的价值只是重现证明的书写过程,学生一定会觉得味同嚼蜡,索然无味(详见文[9])!当知识的逻辑顺序与学生学习的心理顺序比较一致时,教师通过古今对照,从客观的历史发展顺序挖掘适当的素材,给学生优异品格的自然培育提供土壤.
·部分教学设计及分析
环节1 证法探寻.
已知:如图6,△ABC有三个内角∠A,∠B和∠C.
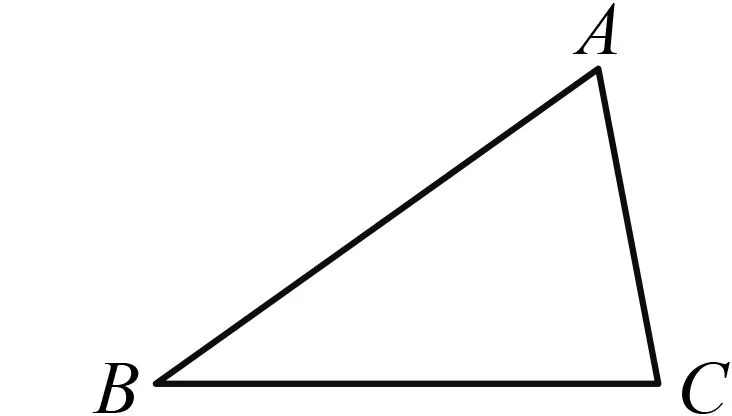
图6
求证:∠A+∠B+∠C=180°.
环节2 古今碰撞.(观看“史话三角形内角和”小视频,详见文[9])
评析从文[9]可以看到,通过不同的证明方法,努力实现“知其然,知其所以然,知何由以知其所以然”,这是理性精神的追求;在教师播放“史话三角形内角和”小视频后,在一声声“小**数学家”称呼的背后,看到学生的喜悦与兴奋,在学生的心中悄然播下对数学爱好与兴趣的种子,给学生营造良好的数学学习的心理状态,在一句句“创新、探索、钻研、自我挑战……”中,数学学科的育人功效悄然发生.
学科教学最终指向人的教育,立德树人是数学学科应当承担的责任.数学发展的历程与人类文明的诞生、发展相伴相随,每一个结论从发现到证明,每一个概念从形成到完善、每一个数学符号从发明到得到公认……无不彰显人类坚韧、挑战与创新的精神力量,数学史中的人文故事是培育学生优异品格的巨大宝藏,教师在课堂教学中,结合所学内容对学生进行潜移默化地培育,以促进学生品格的自然成长.
4 结束语
法国数学家庞加莱(Henri Poincaré,1854—1912)认为,如果我们想要预见数学的未来,适当的途径是研究这门学科的历史与现状.作为数学教师,可能没有时间、精力也没有必要专门研究整个数学学科发展的宏伟历史,但是,我们可以了解与教学内容有关的历史素材,可以根据历史的相似性,洞察学生的学习心理;通过历史发展的轨迹,深入思考数学知识内部的逻辑关系;通过客观存在的历史人文故事,培育学生人格的发展.如案例1,历史让教师更懂学生;案例2,历史让教师更懂数学,让学生感受到学海无涯;案例3,学生不仅与伟大的数学家进行思维碰撞,也接受他们优异品格的熏陶.
遵守教育教学规律,合理安排课堂教学的关键环节,努力让学生的能力与品格随着知识的学习得到自然地发展,是我们不断追求的方向.

