涉及导曲线与分担超平面的正规定则

范楚君， 刘晓俊

（上海理工大学 理学院 上海 200093）

1 问题的提出

正规族理论的核心问题是关于正规定则的研究，其发展主要分为两大板块：一是亚纯函数正规族的研究，这方面的主要方法有Zalcman 引理以及涉及导数的Pang-Zalcman 引理；二是关于一般复流形间全纯映射族的正规定则。

则当t=3,4,5时 ， F在D上正规。

定理6 是对定理4 和定理5 结果的进一步推广。

事实上，对于N=3而 言，当t=3，即超平面处于一般位置时，只须要求 2t+2=8个超平面即可。

2 定义与符号

先介绍 PN(C)相关的定义与符号[5]。

PN(C)=CN+1{0}/～是N维复射影空间。对任意x=(x0,x1,···,xN),y=(y0,y1,···,yN)，x,y∈CN+1{0},x～y当 且仅当存在某个 λ ∈C， 使得(x0,x1,···,xN)=λ(y0,y1,···,yN)。 (x0,x1,···,xN) 的等价类记作[x]=[x0:x1:···:xN]，则

PN(C)上可引入一个自然的度量，即对于点[ω]和 [ω′]之 间的 距 离，采用 CN+1中 2 个圆 γ 和 γ′之间的欧几里得距离来表示，其中， γ 和 γ′分别代表在球面S2N+1上 的这2 个点（这里取 |ω|=|ω′|=1）。简单计算可得

再假设 ω′=ω+dω ， 并舍去关于 |dω|的二阶以上的小量，得到相应的度量形式：

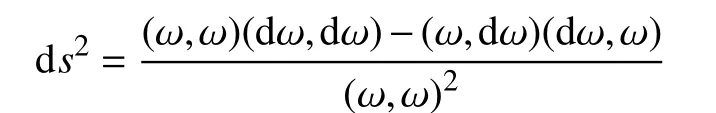
定义1 设U⊂D是 开集，若f0,f1,···,fN在U内全纯且没有公共零点，则称f˜ =(f0,f1,···,fN)是f的一个既约表示。

对全纯曲线f的任何一个既约表示f˜，定义全纯函数

再取

定义2 设f=[f0:f1:···:fN]:D→PN(C)是一个全纯曲线，z∈D， 再设f˜是f在z处的任何一个既约表示，记

其中， αℓ=(aℓ0,aℓ1,···,aℓN)T为非零法向量，ℓ=1,2,···,q。

按照文献[6]中关于t次一般位置的定义，有定义4。

定义4 设N,t,q均 为正整数，且t≥N,q≥2t-N+1。称 超 平 面H1,H2,···,Hq⊆PN(C)处 于t次 一 般 位置，当且仅当对任意集合P⊆{1,2,···,q}， #P=t+1，存在单射µ :{0,1,···,N}→P， 使得Hµ(0),···,Hµ(N)处于一般位置。#P表示集合P中元素的个数是t+1 个。

而对于超曲面的情形，有定义5。

定义5[7]设M⊆PN(C)是一个非空闭子集，t是一个正整数，Q1,Q2,···,Qq是 PN(C)中q(≥t+1)个超曲面，称它们关于M处于t次一般位置，如果对任意 {i0,i1,···,it}⊆{1,2,···,q}，有

3 主要引理

1991 年，Aladro 等[8]将Zalcman 引理进行推广，得出结论：由双曲区域映射到一般的Hermite流形上的全纯映射族仍满足Zalcman 引理。这为正规族理论的发展开创了新的方向。

引理1 设 F是一族从 Cm中 的双曲区域 Ω映到PN(C)的 全纯映射。 F 在 Ω上不正规当且仅当存在子列 {fn}⊂F ，点列 {zn}⊂Ω 满 足zn→z0∈Ω，正数列 { ρn}满 足 ρn→0+，使得

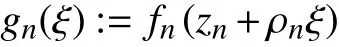
在 Cm上 内闭一致收敛于从 Cm映 射到 PN(C)的非常值全纯映射g(ξ)。

在主要定理的证明过程中，还需要如下的引理2。

引理2(Hurwitz 引理)[2]设 {fn(z)}是定义在区域D⊂C内 的一列全纯函数，a∈C是任意一个复数，且设fn(z)在D的任意一个紧子集上一致收敛于非常值的全纯函数f(z)。 若存在点z0∈D，使得f(z0)=a， 则对于每一个充分大的n， 方程fn(z)=a在D内 有根。此外，存在z0的 某邻域U，使得f(z)-a在U内根的总数与fn(z)-a在U内根的总数相同（计重数）。

1999 年，Eremenko 证 明 了 一 个Picard 型 定理，即引理3。

引理3[9]设f:C →X是一条全纯曲线，其中X是 PN(C)中 的一个闭子集。再设Q1,Q2,···,Q2t+1是PN(C)中 的超曲面，关于X处于t次 一般位置。若f不取Qi， 即〈f,Qi〉≠0, 1 ≤i≤2t+1， 则f必为常映射。

为了便于辅助主要定理的证明，将引理3 推导为引理4。

引理4[7]设f:C →PN(C)是一条全纯曲线，H1,H2,···,Hq均 是 PN(C)中 处于t次一般位置的超平面，其中，q≥2t+1,t≥N，若对每个i∈{1,2,···,q}，f不取Hi， 或者f(C)⊆Hi，则f必为常映射。

引 理5[3]设g=[g0:g1:···:gN]:C →PN(C)是一条有穷级的全纯曲线，且g0(ζ)≢0，N≥2是一个整数。Hℓ={x∈PN(C):〈x,αℓ〉=0}是 PN(C)中处于一般位置的超平面，且其第一系数aℓ0均不为零，ℓ=1,2,···,N+1.g˜(ζ)=(g0,g1,···,gN)(ζ)是g的 任 意既约表示，令

若Gℓ(ζ)≠0且Gℓ′(ζ)≠0, ζ ∈C ， 则g是线性退化的。

引理6[10]设f(z)为 整函数，若f(z)的球面导数f#(z) 有 界，则f(z)的级最多为1。

4 主要定理的证明

4.1 定理3 的证明

b.若p2=0 ， 则p0,p1不全为零。

(a)若p1≠0 ， 则g1,g3可 由g0,g2线 性 表 出，类似于a 的证明，矛盾；

(b)若p0≠0,p1=0 ， 而g0≠0，矛盾。

因此， F在D上正规。

当N=3，t≥4时 ，所需超平面的个数会随着t值的增长而增加。目前，仍未能找到明确的上界。