基于深度学习和单目摄影测量的混凝土表面裂缝测算方法
王 浩,金银龙,刘 全,张宏阳,马骏骁
(武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
0 引 言
近年来,中国水利、桥梁、隧道等基建工程数量及规模都领先世界,其安全运营及管理对保障国民经济具有重要意义。而裂缝作为这些基建工程常见的病害问题之一,存在着重大安全隐患,应该引起足够重视[1]。传统人工检测方法,难以满足现代工程领域对高效率、高精度的裂缝检测需求。同时在国家大力推进工程智能化、信息化建设的背景下[2],研究新兴智能化技术在混凝土裂缝检测中的应用具有重要意义。
目前,许多学者将深度学习、计算机视觉等新兴技术应用到混凝土裂缝识别检测中,并取得了很大进展。孟庆成、Ni等[3-4]基于机器视觉理论搭建了ResNet18网络模型框架对混凝土裂缝图像进行识别,取得良好效果。刘新根等[5]使用两个深度卷积神经网络实现了对隧道衬砌和裂缝图像的分类识别。CHA,JANG等[6-7]使用卷积神经网络的深层结构来检测混凝土裂缝。章世祥等[8]采用卷积神经网络Mask R-CNN为主干框架,融入ResNet模型与特征金字塔网络(FPN)建立了裂缝病害识别网络体系。韩晓健、苑玮琦、周颖等[9-11]基于计算机视觉对混凝土裂缝识别分割处理,识别精度较高,但处理效率较低。
而在混凝土裂缝特征提取方面,主要是在裂缝图像识别的基础上,运用数字图像处理技术对图像中裂缝占有的像素点数进行量测,常用的图像处理方法包括边缘检测、阈值分割、骨架提取等[12-13]。也有学者通过做场景标记换算图像像素对应的实际距离,来估算裂缝在三维场景的实际长度、宽度等几何特征。缪盾[14]基于Canny算法计算边界像素来测量裂缝的像素长度和宽度,并通过像素解析度求得实际长度。王一兵等[15]采用VDM粒子测量方法计算裂缝面积和宽度,并对识别结果进行骨架提取,进而计算长度。这些方法本质上还是计算像素点所代表的尺寸。但是相机是根据凸透镜成像的原理制成的,所拍摄的物体并不是按照固定比例缩放到图像中,每像素换算到三维场景中,所代表的尺寸是变化的[16-19]。因此,仅通过换算像素对应的尺寸来计算裂缝的几何特征会造成较大偏差。
综上,人工检测混凝土表面的方法效率低,而现有智能检测方法多是对裂缝图像的识别,未能给出计算裂缝实际几何特征的测算方法。为此,本文基于深度学习算法设计了裂缝检测模型,实现了混凝土表面裂缝高效率、高精度的自动检测;并基于单目摄影测量原理,分析二维裂缝图像与三维空间场景间的空间尺度对应关系,给出系统可靠的计算裂缝几何信息的理论方法,实现了基于二维图像提取裂缝实际几何信息。该方法解决了目前根据混凝土表面裂缝图像难以精准提取实际空间几何信息的难题,为该领域的工程人员提供了一定的技术支持。
1 理论基础与技术路线
针对混凝土表面裂缝检测和几何信息提取问题,本文结合深度学习和单目摄影测量技术提出一种快速有效的裂缝测算方法。该方法基于Unet深度学习算法设计裂缝检测模型,可以达到像素级别的识别结果,有效提高了裂缝图像的分割精度,并且Unet网络能从较少的训练图像中,依靠数据增强方法有效利用有限标注数据实现Unet深度学习模型的训练,完成影像特征的识别[20-21]。同时,基于单目摄影测量技术分析二维裂缝图像与三维场景间的空间尺度对应关系,探索了相机以不同角度拍摄裂缝平面时,图像像素对应的实际空间尺寸分布情况和变化规律,进而确定裂缝像素对应的空间几何尺度;然后利用数字图像处理技术基于裂缝图像的空间尺度对应关系计算裂缝几何信息。本方法的技术路线具体如图1所示。
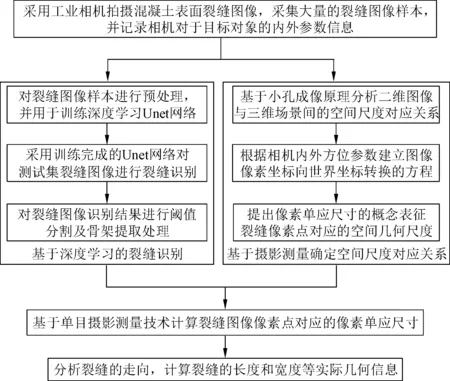
图1 混凝土表面裂缝测算方法技术路线Fig.1 Technical route of concrete surface crack measurement method
2 基于深度学习的裂缝识别
2.1 样本准备和预处理
采用工业相机采集不同混凝土建筑物表面裂缝图像,并记录相机的内外方位参数。本实验共采集了1 000张各类混凝土裂缝照片,裂缝形态包括单条裂缝、分叉裂缝和裂缝网络。从样本集中,随机选取700张裂缝图像作为卷积神经网络的训练集,剩下的300张作为用于测试裂缝模型识别效果的测试集。
相机直接获取的裂缝图像尺寸大,包含许多无关背景信息,并且由于裂缝样本图像采集时,相机外方位参数是随机的,裂缝图像的缩放比例并不一致。为消除背景图像的影响,改善图像质量,需要对裂缝图像进行预处理。预处理方法包括:① 将样本图像以500×500像素的裁剪框进行裁剪;② 采用双边滤波法对混凝土表面裂缝进行降噪平滑处理;③ 对裂缝图像进行二值化,以白色表示背景,黑色表征裂缝。
2.2 Unet模型训练
数据增强:由于训练集图片仅有700张,数目远低于正常训练集的5 000张要求,对输入的训练集图像做了数据增强处理,主要处理包括图片锐化增强、随机翻转、随机噪声处理以及自动对比度调整。由此扩展训练集样本数,使Unet神经网络得到更为充分的训练。
参数设置:等间隔调整学习率StepLR,每训练20次,学习率会乘以0.8;本模型的Loss函数使用计算二分类的交叉熵函数,其中的Loss权重设定如下:背景Loss权重设为0.05,裂缝Loss权重设为2.0;将一次抓取的样本数量定为16,训练次数epoch为100次。使用Adam优化器,权重增值为1×10-4,学习率设为1×10-4。
训练过程:更新一个epoch循环表示训练中的所有训练样本均被使用过一次,随机开始下一轮循环,一共完成100个循环。执行代码开始训练后,载入初始未经训练的Unet裂缝分割算法模型,分批次将训练所用的图片与标签输入到网络中,一个epoch后进行梯度清零、损失函数计算、反向传播和模型的参数更新。每个循环保存一次权重参数,之后的验证环节使用第100个循环生成的权重文件进行预测。
2.3 裂缝识别结果分析
采用训练完成的Unet裂缝检测模型对测试集中未经训练的300张混凝土表面裂缝进行识别。图2中展示了典型的单条裂缝、分叉裂缝和裂缝网络的识别结果,可见训练后的Unet模型可识别出图像中的混凝土裂缝(图像中红色标记区域)。

图2 混凝土表面裂缝图像识别结果Fig.2 Concrete surface crack image identification results
图3展示了Unet模型的准确率变化情况,在训练集与测试集上准确率均超过95%,表明模型预测图像有无裂缝的结果与训练集标签显示一致的比例达到95%以上,识别结果准确可靠。
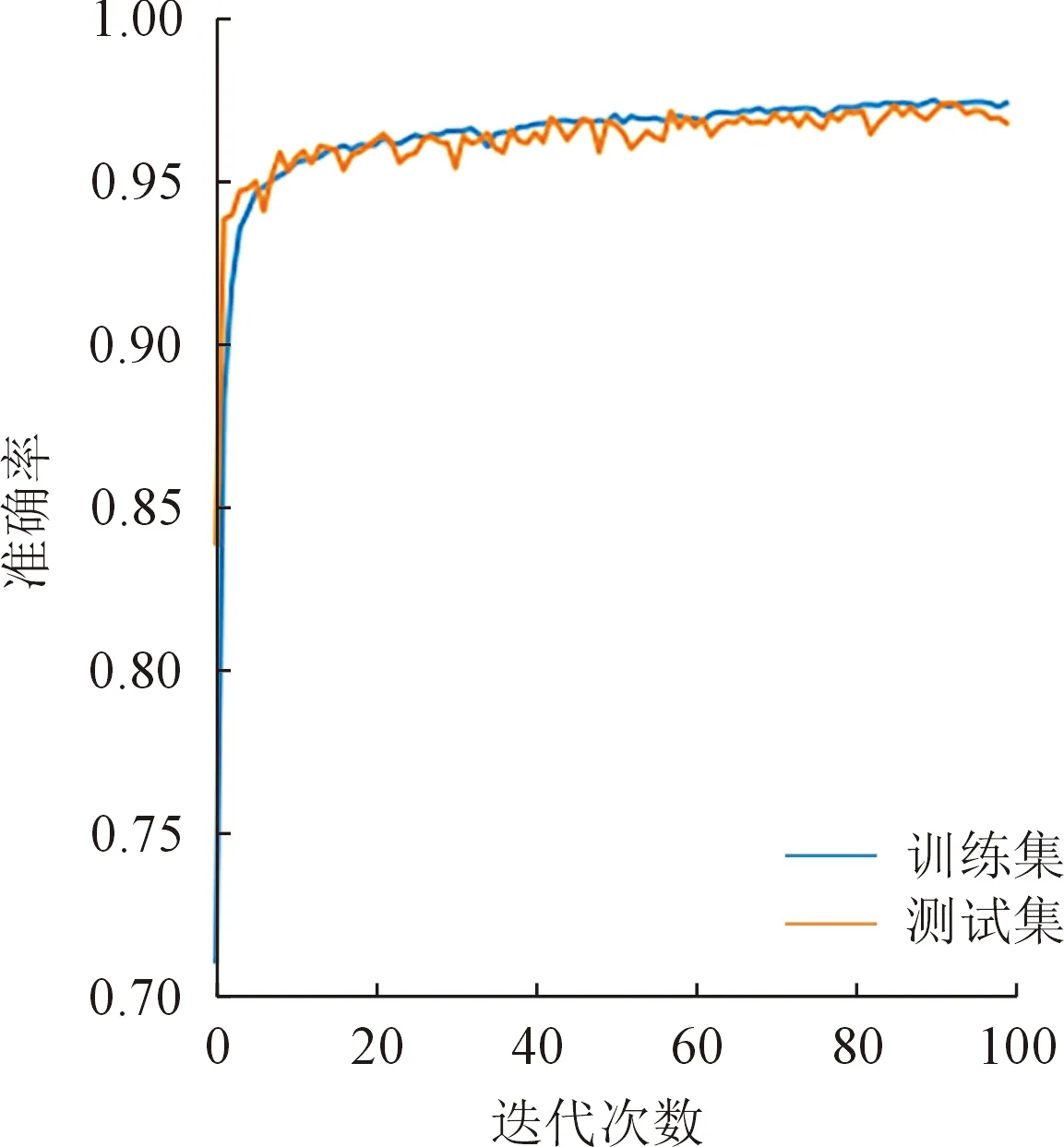
图3 准确率变化情况Fig.3 Changing trend of accuracy
2.4 阈值分割
虽然Unet模型可以实现对图像中裂缝的准确识别,但对于细小裂缝或存在较大倾斜角度的裂缝图像,裂缝清晰度会被稀释模糊,模型无法准确判别裂缝与背景的分界线,导致分割的裂缝宽度大于实际裂缝宽度,如图4(b)所示。因此需要对模型的裂缝识别结果进行精细分割,提高裂缝识别的精度。
Unet模型在识别裂缝过程中,可以对预测裂缝像素进行色彩处理,使整幅图像中,背景区域与实际裂缝区域的RGB值存在明显差异。然后基于RGB进行阈值分割处理,更精细地提取图像中裂缝所在区域。同时为便于计算裂缝宽度特征,将裂缝图像进行二值化处理,实际裂缝所在区域标为白色,其他区域为黑色,结果如图4(c)所示。

图4 阈值分割处理后的结果对比Fig.4 Comparison of results after threshold segmentation
2.5 裂缝骨架提取
混凝土表面裂缝图像经过模型识别和阈值分割后,裂缝在图像中的实际区域已经被提取出来。为了方便分析裂缝的走向和长度特征,需要对裂缝进行骨架提取,将多像素点宽度的裂缝转换成单像素点宽度的图像。
采用K3M算法对阈值分割后的图像进行骨架提取,结果如图5所示。可以看出骨架线与模型识别地裂缝区域宽度相差较大。虽然在裂缝破碎带区域,提取的骨架线仍不满足单像素点宽度的提取目标,但像素点数量已经大量减少,有利于计算裂缝走向和长度等特征。

图5 裂缝骨架线提取结果Fig.5 Extraction results of fracture skeleton line
3 基于摄影测量的裂缝信息提取
基于上述裂缝图像识别结果,根据摄影测量技术确定的二维裂缝图像与三维场景间的空间尺度对应关系,可以计算裂缝的实际几何信息。具体方法如下所述。
3.1 确定空间尺度对应关系
3.1.1 成像模型
单目摄影测量技术是利用一台拍照设备获取单张图像,根据二维图像信息以立体视觉原理恢复场景的三维空间信息,实现对空间对象的几何信息提取。这种方法本质上是利用小孔成像的原理,通过图像像素坐标系向世界坐标系的转换,确定像素与三维空间场景的几何关系,计算图像上每个像素恢复到三维场景中对应的实际尺寸大小,进而计算目标对象的几何特征。该方法需要依次完成像素坐标系向图像坐标系、相机坐标系以及世界坐标系的转换。
图6中展示了4个坐标系之间的关系,其中坐标系Ouv-uv为像素坐标系;O-xy为图像坐标系;OC-XCYCZC为相机坐标系;Ow-XwYwZw为世界坐标系;P(Xw,Yw,Zw)为世界坐标系中的一点,p(x,y)是世界坐标系中点P在图像中的投影,根据摄影测量原理和几何关系可得下列坐标转换关系式,并用齐次坐标系与矩阵形式表示。
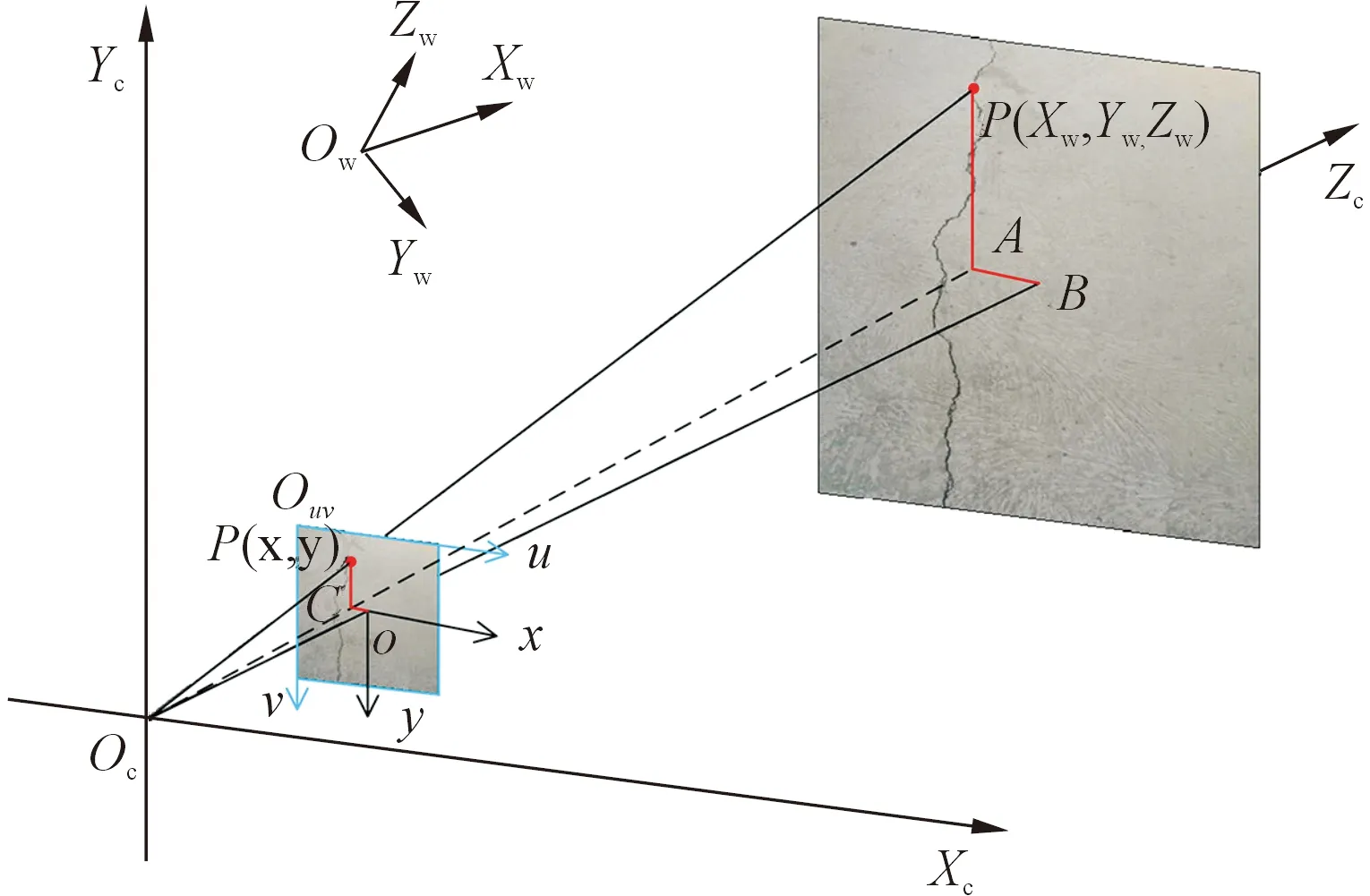
图6 4个坐标系之间关系示意Fig.6 Schematic diagram of the relationship between the four coordinate systems
(1) 像素坐标系向图像坐标系转换
(1)
(2)
式中:dx,dy分别为每个像素在图像平面上的物理尺寸;u0,v0分别表示原点平移的距离,即图像坐标系在像素坐标系中的坐标。
(2) 图像坐标系向相机坐标系转换,根据三角相似关系可得:△OCOC∽△OCAB,△OCpC∽△OCPA,则点P在相机坐标系与像平面坐标系中的关系满足:
(3)
(4)
式中:f为相机焦距,mm;x,y分别表示物体在像平面坐标系下的坐标点,pixel。
(3) 相机坐标系向世界坐标系转换
(5)
式中:R为旋转矩阵,描述了相机坐标系相对于世界坐标系的旋转变量;T为偏移矩阵,描述相机位标系相对于世界坐标系的平移变量。
3.1.2 裂缝倾斜影像的空间尺度转换
按照式(1)~(5)可实现像素坐标向世界坐标的转换,但这要求像平面与物平面(裂缝所在三维空间平面)平行,即相机要正对混凝土裂缝平面拍摄,否则在图像坐标系向相机坐标系转换时,不满足三角相似关系,进而通过式(1)~(5)实现像素坐标系向世界坐标的转换是不正确的。
然而在实际工程中,存在一定倾斜角度的混凝土裂缝平面是非常常见的,同时由于裂缝所处位置较高或者较偏,难以保证相机正对混凝土裂缝平面拍摄,即像平面与裂缝平面一般不平行,使裂缝图像存在倾斜角度,如图7所示。为探究裂缝图像存在倾斜角度时,二维裂缝图像与三维场景间的空间尺度对应关系,作出以下假设。
与像平面平行的物平面为理想物平面,裂缝实际平面与理想物平面之间的夹角为θ。根据摄影测量原理,实际裂缝平面一点P,在理想物平面上对应点为P′;B′为相机光轴与理想物平面的交点;直线BP垂直相机光轴;A,A′分别为点P,P′在平面OC-ZCXC上的投影点;直线DE是裂缝实际平面和理想物平面的交线;∠α是直线AOC与相机光轴的夹角;∠β是直线AOC与直线POC的夹角;∠γ是直线POC与相机光轴的夹角。

图7 裂缝倾斜图像的空间尺度转换示意Fig.7 Spatial scale transformation of crack tilt images
根据空间几何关系,只要确定了直线POC的距离L,∠α,∠β,∠γ即可通过式(6)求出点P在相机坐标系中的位置。
(6)
实际拍摄中,不管相机以何种角度拍摄裂缝,相机光轴与裂缝实际平面总存在交点B′,即能对于裂缝实际平面上任一点P确定平面Oc-PB′,并通过点B′确定理想物平面。找到理想物平面后,即可根据式(1)~(4)确定点P′在相机坐标系中的坐标,进而根据三角关系求出∠α,∠β,∠γ的大小。然后在三角形OcPB′中,已知两角夹一边,根据正弦和余弦定理,即可求出直线POC的距离L的值。
通过上述方法可以确定存在倾斜角度的裂缝平面上一点在相机坐标系中的位置。然后联合式(1)~(6)确定图像像素在世界坐标系的位置,为方便表示将其简写为
P(Xw,Yw,Zw)=F(p(u,v))
(7)
式中:F表示像素坐标系与世界坐标系之间的对应关系。
3.1.3 像素单应尺寸确定及其分布规律
像素单应尺寸是指二维图像中每个像素对应到三维空间场景中的实际尺寸大小,单位为mm/pixel。而每个像素对应的像素单应尺寸Δd,可以通过两个斜对角像素的间距换算到三维空间所对应的实际尺寸进行计算,如图8所示,计算方法如式(8)所示:
(8)
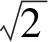

图8 像素单应尺寸计算示意Fig.8 Diagram for calculating pixel homography size
以图像光心点为中心,分别计算当相机分别以与水平面存在0°,15°,30°以及45°的角度拍摄裂缝图像时,即裂缝图像倾斜角度分别为0°,15°,30°以及45°时,裂缝图像中某一直线上的像素对应的像素单应尺寸随着像素到中心的距离分布规律,如图9所示。
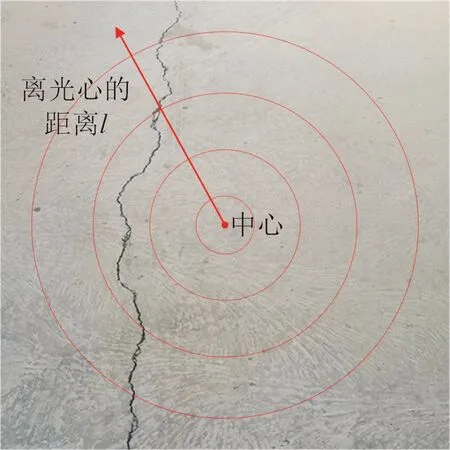
图9 分布规律计算方法示意Fig.9 Diagram of calculation method for distribution regularity
计算结果如图10所示,可以发现:

图10 像素单应尺寸变化规律Fig.10 Change regularity of pixel homography size
(1) 裂缝图像倾斜角度不为0°时,即相机非正对裂缝平面拍摄,像素单应尺寸随着到中心的距离增大而增大;同一距离处,裂缝实际平面与理想物平面夹角越大,对应的像素单应尺寸越大;裂缝图像倾斜角度越大,像素单应尺寸变化不均匀程度越大。
(2) 裂缝图像倾斜角度为0°时,即相机正对裂缝平面拍摄,此时像素单应尺寸是均匀分布的,图像中每个像素对应到三维场景中的几何尺寸大小是均匀不变的。
以裂缝图像倾角30°为例,探究图像中每个像素对应的像素单应尺寸分布规律,结果如图11所示。从图11中可知:每一列像素点(u轴)两端的像素单应尺寸较大,中间较小,这符合图10中的规律,即越偏近中点,像素对应的实际尺寸越小;每一行像素点(v轴)两端的像素单应尺寸较小,中间较大,是因为裂缝平面与理想物平面是以u轴为交线形成夹角的,造成每一行中间部分的像素对应的三维场景坐标之间梯度较大,进而像素单应尺寸较大。

图11 倾角30°对应的像素单应尺寸分布规律Fig.11 Distribution regularity of pixel homography size corresponding to inclination angle of 30°
3.2 计算裂缝几何信息
以图4(a)为例,采用工业相机采集裂缝样本,并记录相机的内外参数,如表1所示。在第2节对该裂缝图像的处理结果的基础上,基于单目摄影测量理论计算裂缝的走向、宽度以及长度。

表1 相机内外参数设定
3.2.1 计算裂缝走向
基于裂缝骨架提取的结果,获取图像中裂缝骨架所占有的像素,然后根据像素坐标进行线性回归拟合,拟合的结果如图12所示,拟合得到裂缝骨架像素行列坐标之间的关系为
col=-0.07455×row+179.01587
(9)
式中:col,row分别表示像素列、行坐标。
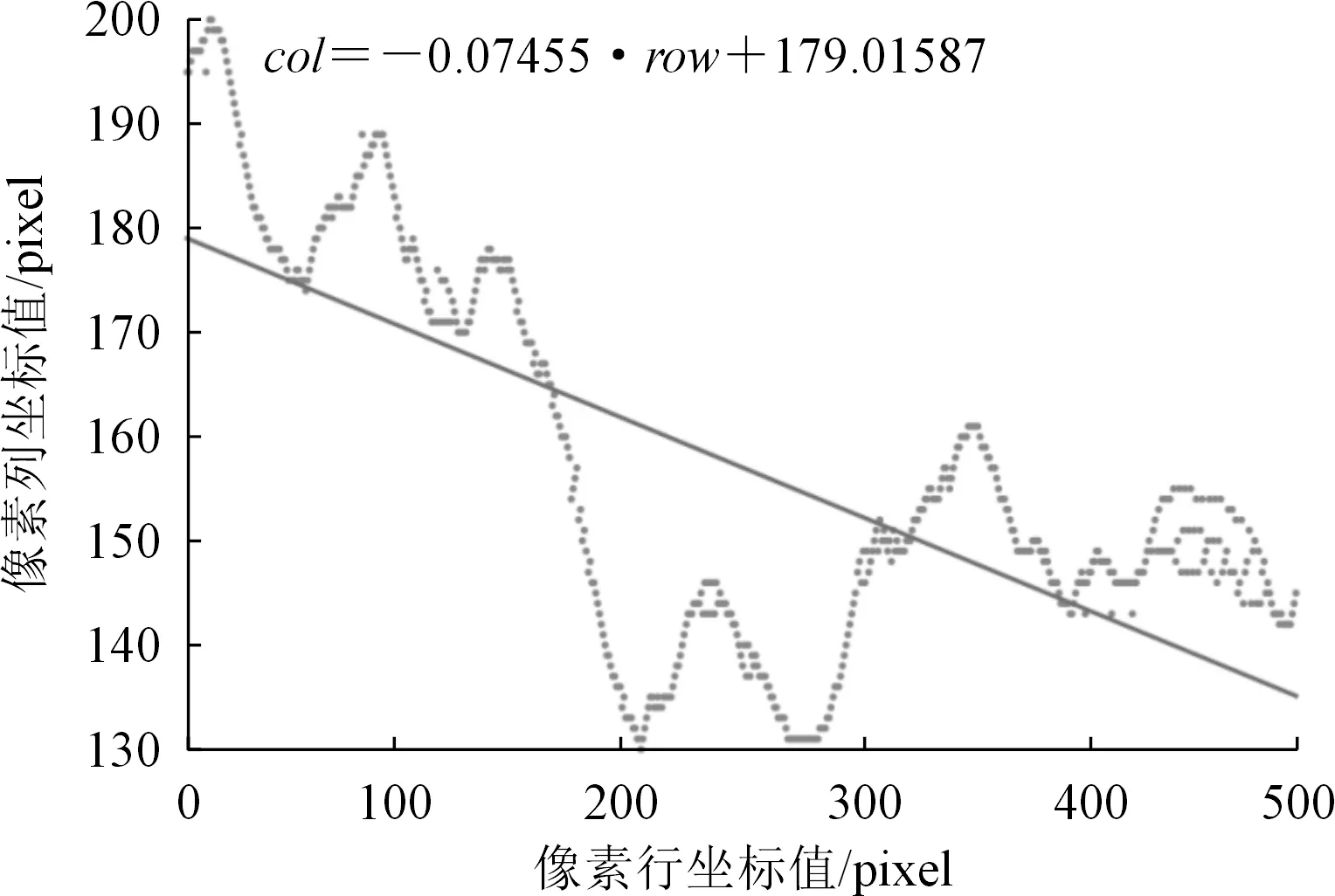
图12 线性回归拟合Fig.12 Linear regression fitting
根据式(9)计算该线性方程在裂缝图像上的分布,检查拟合的结果是否可靠。如图13所示,可见拟合的结果符合裂缝图像像素分布。然后根据线性方程的斜率计算得到,该裂缝图像的走向与垂直方向的夹角为4.26°,进而裂缝的实际走向可通过相机外方位参数换算得到。

图13 图像中裂缝走向Fig.13 Crack direction in the image
3.2.2 计算裂缝宽度
裂缝宽度可以用与裂缝图像走向垂直的方向上裂缝开裂尺寸大小表示。因此,需要根据裂缝图像走向,将裂缝阈值分割后的结果(图4)逆时针旋转4.26°,使裂缝图像走向线竖直,结果如图14所示。然后计算每行中裂缝像素点的个数,并根据式(1)~(7)计算每个像素对应的像素单应尺寸,如图15所示。再将每行的裂缝像素对应的像素单应尺寸进行累加,即可得到裂缝图像中每行像素对应的裂缝实际宽度,进而通过比较每行裂缝宽度得到裂缝最大宽度,计算方式如式(10)所示。裂缝最大宽度的计算结果为21.13 mm。

(10)
式中:Erow表示图像的第row行中位于裂缝区域的像素集合。

图14 裂缝图像旋转结果Fig.14 Crack image rotation result

图15 裂缝像素对应的像素单应尺寸Fig.15 Pixel homography size of crack pixels
3.2.3 计算裂缝的长度
根据裂缝图像骨架提取结果(图5),利用式(1)~(7)计算图像中裂缝骨架像素对应的像素单应尺寸(图15),然后利用式(11)对裂缝骨架像素对应的像素单应尺寸进行积分,即可得到裂缝的长度,计算结果为0.967 m。

(11)
式中:E为图像中裂缝骨架所在像素的集合,p(u,v)∈E。
4 案例结果分析
本文基于深度学习设计裂缝检测模型并进行训练,采用未经过训练的裂缝图像进行模型检测实验,分析二维裂缝图像与三维场景间的空间尺度对应关系,进一步提取了该图像中裂缝的实际几何信息。实验内容和结果包括:
(1) 基于Unet深度学习算法设计的混凝土表面裂缝检测模型,可以实现高效率、高精度的裂缝自动检测识别,识别准确率可达95%(表2)。但是,对于细小裂缝或者拍摄存在较大的倾斜角度的裂缝图像,裂缝清晰度会被稀释模糊,模型无法准确判别裂缝与背景的分界线,导致分割的裂缝宽度大于实际裂缝宽度,因此需要结合阈值分割法进行精细分割,提高裂缝的分割精度。

表2 多个裂缝样本的几何信息测算精度
(2) 基于单目摄影测量技术分析二维裂缝图像与三维场景间的空间尺度对应关系,研究发现:当裂缝影像倾斜角度为0°,即相机正对裂缝平面拍摄时,像素对应的三维场景中实际尺寸是均匀分布的,这是现有文献研究的适用情况;而当裂缝影像倾斜角度不为0°,即相机非正对裂缝平面拍摄时,像素对应的三维场景中的实际尺寸是变化的,现有研究方法就不再使用,具体呈现的分布规律为:越远离图像光点,像素单应尺寸越大;倾斜角度越大,像素单应尺寸均匀性越低。
(3) 基于Unet模型识别结果和单目摄影测量技术确定的空间尺度对应关系,利用图像处理技术计算裂缝走向、长度和宽度等几何信息。对于本案例中的单条裂缝,实际人工测量的最大裂缝宽度约为20 mm,长度约为1.05 m,可见采用本方法的计算结果与实际人工测量结果相近。采用式(12)计算本方法的测算精度,可得裂缝最大宽度测算精度为94.4%;长度测算精度为92.1%。采用同样的方法对测试集中多个裂缝样本进行实验,对于交叉裂缝和裂缝网络先将其分为单条裂缝,再计算其长度和宽度信息。裂缝几何信息测算精度结果如表2所示。

(12)
可见,采用本方法计算得到的长度和宽度信息与人工测量结果相近,精度可达90%,验证了本方法的可靠性。
5 结论与展望
针对混凝土表面裂缝图像识别及几何特征提取难题,本文提出了一种基于深度学习和单目摄影测量的混凝土表面裂缝几何信息测算方法。首先采用Unet网络实现对裂缝图像的快速准确识别,准确率可达95%;并基于单目摄影测量原理建立二维图像与三维空间场景间的尺度对应关系,分析相机以不同角度拍摄裂缝平面时,裂缝图像对应的空间尺度分布规律,给出了系统可靠的计算裂缝几何信息的理论方法;然后在裂缝图像识别的基础上,基于裂缝图像的空间尺度对应关系计算裂缝走向、长度以及宽度等几何信息,通过与人工测量结果进行比较,测算精度可达90%,验证了本方法的可靠性。可见,本方法可以实现基于裂缝二维图像较精准计算裂缝实际几何信息,推进了深度学习在实际工程中的应用,为运用新兴智能技术解决传统工程问题提供了一种新思路。但本研究未考虑对裂缝破碎带的处理以及裂缝长度计算还存在一定的误差,因此今后还需进一步分析研究。

