块度预报模型在南水北调中线工程渠首爆破开挖中的应用

陈宗光，谢洁方

(1.中国电建集团 中南勘测设计研究院有限公司，湖南 长沙 410014； 2.湖南劳动人事职业学院 建工系，湖南 长沙 400100)

0 引 言

南水北调工程是中国重大战略性跨流域水资源配置工程，旨在解决北方地区水资源短缺问题[1]。南水北调中线渠首枢纽工程地处丹江口水库东部，位于汤山与禹山之间的垭口地带，区内主要地貌单元有：剥蚀残山、垄岗、水系及人工地貌等。工程区内地表多为第四系覆盖，基岩主要出露奥陶系中统第二岩组(O22)、第三岩组(O23)及白垩—下第三系(K～E)。受多期构造作用的影响，褶皱、断裂较为发育。断层主要发育北西西向和北北东向两组，规模一般不大。裂隙以陡倾角为主，闸基岩体未发现倾缓角裂隙。南水北调中线渠首枢纽工程爆破开挖中，要求尽量减少钻孔量和降低单耗，确定合理、高效的爆破孔网参数，尽量降低爆破呈现石块的大块率，减少孤石解炮的次数，以达到降低成本的要求。以往研究中，通常在有级配要求的规格石料生产(如堆石坝填筑料生产)时，采用爆破块度预报模型进行爆破效果评估，以调整爆破方案，控制爆破效果[2-4]。然而，在水工建筑物岩石基础或地下厂房爆破开挖过程中，需严格控制保护层开挖效果，建立爆破平均块度预测模型，有利于避免超欠挖问题。本文通过选取或者建立合理的爆破块度分布模型来预测爆破块度，使之满足设计级配要求，动态调整确定相应的爆破参数，以指导现场施工。

1 KUZ-RAM爆破块度预测模型

从20世纪50年代起研究人员就开展了对爆破块度分布的研究，提出了一系列爆破块度预报模型。主要包括4类：能量理论模型、应力波理论模型、块度分布函数模型以及新近发展起来的损伤力学模型，比较有代表性的分别有GAMA模型、G·Harries模型和KUZ-RAM模型等[5]。

KUZ-RAM块度预报模型[6-7]在矿山应用多年，虽然在水利水电工程爆破中进行块度预报存在一定误差，但可以利用爆破试验资料对模型进行适当修正，提高预报精度。该模型建立了各种爆破参数(如最小抵抗线W，孔距a，炸药单耗q，台阶高度H，凿岩精度和炮孔直径d等)与爆破块度分布的定量关系，便于将这些参数与爆破块度分布进行量化分析。而且，这些参数都是已知的，数形结合、形象直观，便于推广应用。计算爆破平均块度时，运用了综合性很强的岩石系数A，该系数反映了岩石物理力学特性和节理裂隙情况的影响，真实还原现场地质情况。再结合现场监测数据对模型进行修正，提高预测精准度。

KUZ-RAM模型是一个典型的露天台阶式开采爆破数学模型，从基本组成和各参量的数学定义来看，适用条件为[8]：① 炮孔为向下平行布置，连续柱状装药；② 爆破延时一般在毫秒范围内的群孔爆破，而不适宜于单孔爆破；③ 炸药性能主要由密度和相对威力来描述；④ 岩石性能主要由强度指标和节理性质来描述和计算；⑤ 炮孔堵塞性能好，集中起爆。南水北调中线工程渠首爆破采用连续柱状装药，采用毫秒延时的群孔爆破，且炮孔性能良好，因此，可以采用KUZ-RAM模型估算爆破后的块度尺寸范围。

1.1 预测原理

KUZ-RAM模型的基本表达式由Kuznetsov方程[9]、Rosin-Rammler分布函数[10]和块度不均匀系数[11]n计算式组成：

(1)

R=1-exp[-(X/X0)n]

(2)

n=(2.2-14W/d)(1-e/W)

[1+(m-1)/2]L/H

(3)

1.2 块度预报

在爆破开挖现场收集了多组爆破开挖的孔网参数及块度分布数据，本文选取8组数据进行分析，具体爆破孔网参数如表1所示。

表1 渠首开挖工程右岸爆破孔网参数

表2 KUZ-RAM模型计算值

通过以上研究发现，该模型反映的爆破块度分布线性特征和变化趋势与实际情况大体保持一致。将模型计算结果与现场实测数据对比分析，如表3所示。

表3 模型计算n值和平均块度值与实测结果的比较

2 KUZ-RAM模型修正

将爆破试验收集的实际块度分布资料与模型计算的平均块度和块度不均匀性指数n进行比较，分别对实际值和计算值进行回归分析，得出模型修正前后计算值的关系式，最终确定修正后的KUZ-RAM模型。

2.1 关于岩石系数A的修正

岩石节理和裂隙对爆破的块度分布有很大影响。岩石本身的强度、密度和破碎性等性质与爆破块度密切相关，采用岩石系数A反映这些影响和关系。应考虑岩石物理力学性质和节理裂隙发育情况的综合性指标。模型中规定的几种不同情况的取值，无法全面、客观地反映不同岩性、不同节理裂隙开度及分布对岩石破碎块度的影响。Cunningham CVB[4]用现场反馈的实际资料进行改进和修正，提出确定岩石系数A的新方法，并给出了式中各值的取值方式：

A=0.06(RMD+JF+RDI+HF)

(4)

其中，RDI=25RD-50；E<50 GPa时，HF=E/3；E≥50 GPa时，HF=UCS/5。

式中：RMD为岩体性能系数；JF为节理特征系数；RDI为密度系数，g/cm3；RD为密度，g/cm3；HF为硬度系数；E为弹性模量，GPa；UCS为抗压强度，MPa。

2.2 关于平均块度计算公式的修正

图1 平均块度实测值与计算值回归直线Fig.1 Regression line between measured and calculated average lumpiness

(5)

为了验证修改后公式的效果，将表1中的爆破孔网参数代入到公式(5)中，并与原模型计算值比较(表4)。由表4可看出，模型修正后平均块度的计算值与实测值的相对误差，相较于原模型平均块度的计算值与实测值的相对误差，有了大幅度降低，预报准确性得到了保证。

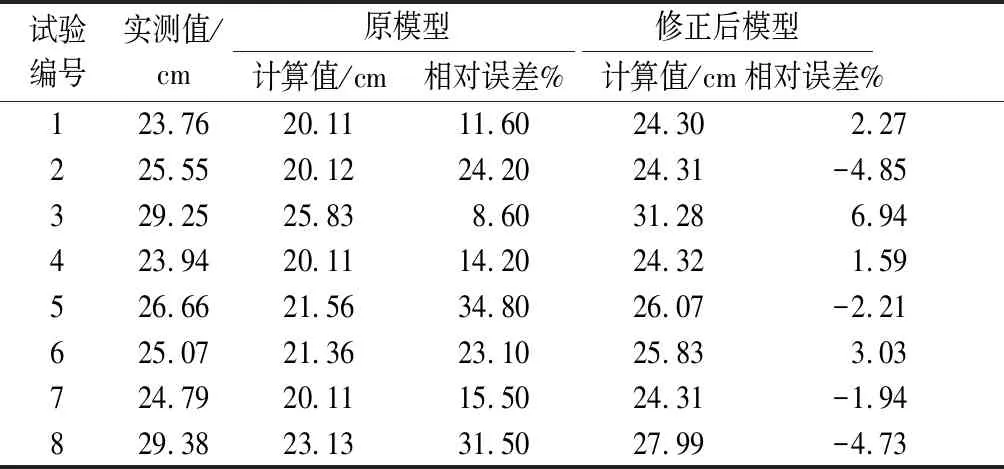
表4 模型修正后平均块度计算值与原模型计算值比较

若用平均块度的实测值作为横坐标，用模型修正后平均块度的计算值作为纵坐标，将两者进行回归分析(图2)。

图2 平均块度实测值与模型修正后的计算值回归直线Fig.2 Regression line the measured value of average lumpiness with the calculated value after model modification

由图2可看出，回归直线斜率接近于1，截距可忽略不计，相关系数|R|=0.89。当α=0.01时满足置信区间，认为率定参数满足精度要求。由此可见，平均块度的实测值与模型修正后的计算值高度相关。修正后的平均块度计算公式(5)比原模型的计算式(1)误差较小，预报更为精确。

2.3 关于n值计算公式的修正

n′=

(6)

(7)

原模型适用的块度不均匀指数n在0.8～2.2之间，经修正后的爆破块度模型适用的n值在0.7～1.0之间，原模型在南水北调中线渠首爆破开挖工程中的应用得到了延伸。

2.4 修正后模型工程应用情况

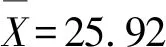
表5 工程应用中原模型与修正后模型的对比

(2) 进行爆破参数优化的可能性。利用修正后的KUZ-RAM模型对爆破参数进行优化设计，能够降低爆破开挖成本，提高工程的经济性。为了验证这一结论，选取一组未按照修正后的KUZ-RAM模型进行优化设计的爆破试验参数(表6)。

表6 未按照模型进行优化设计的爆破试验参数

由表6可知，未按照模型进行优化设计时，单耗q=0.35 kg/m3，居于0.25与0.48之间，可优化的空间仍然较大。

3 结 论

结合南水北调中线工程渠首现场爆破试验数据，对KUZ-RAM模型进行了修正，以实现对工程中的爆破块度更为准确的预报。主要结论如下：

(1) 应用KUZ-RAM模型作为预报爆破块度的基本模型是可行的，但其所确定的块度分布与实际情况有较大出入，在实际工程应用中应加以修正。

(2) 本文对KUZ-RAM块度预报模型的岩石系数、平均块度及块度不均匀系数的计算式进行了修正，在进行块度预报时，相对误差较小，预报更为精确。

(3) 基于工程试验数据对KUZ-RAM 模型进行了修正，可实现对爆破孔网参数的优化设计，减少钻孔量和降低单耗，达到降低开挖成本、提高经济性的目的。

然而需要指出的是，该模型的修正公式是基于南水北调中线工程渠首爆破开挖试验数据得出的，因此适用范围存在局限性。在其他工程条件下，应根据实际情况进行修正，结合地质和地形等特征的变化进行动态调整。