一道新高考导数压轴题的分析与延伸
雷 蕾 (江苏省南京市第一中学 210001)
2022年新高考I卷第22题是一道函数与导数综合的压轴题,考查了利用导数研究函数的极值与最值、零点等知识,体现了分类讨论、数形结合、函数与方程、转化与化归等数学思想,对学生的逻辑推理、直观想象、数学运算等核心素养要求较高.下面笔者从分析高考真题、推广一般结论、探究其他性质这三个方面展开,对这道压轴题进行深度解析,供大家参考.
1 分析高考真题,厘清解题思路
试题(2022年新高考I卷第22题)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.
(1)求a;(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.
思路 (1)分2步:①分别求出f(x)与g(x)的最小值(用a表示),由f(x)与g(x)的最小值相等建立关于a的方程;②利用导数求解关于a的方程.
(2)分3步:①证明f(x)与g(x)的图象只有一个交点(x0,y0);②证明直线y=y0与f(x),g(x)的图象各有另一个交点;③证明从左到右的三个交点的横坐标成等差数列.
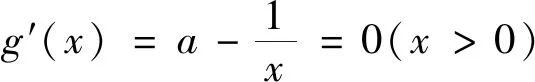
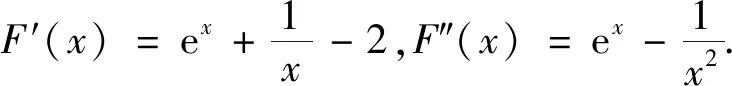
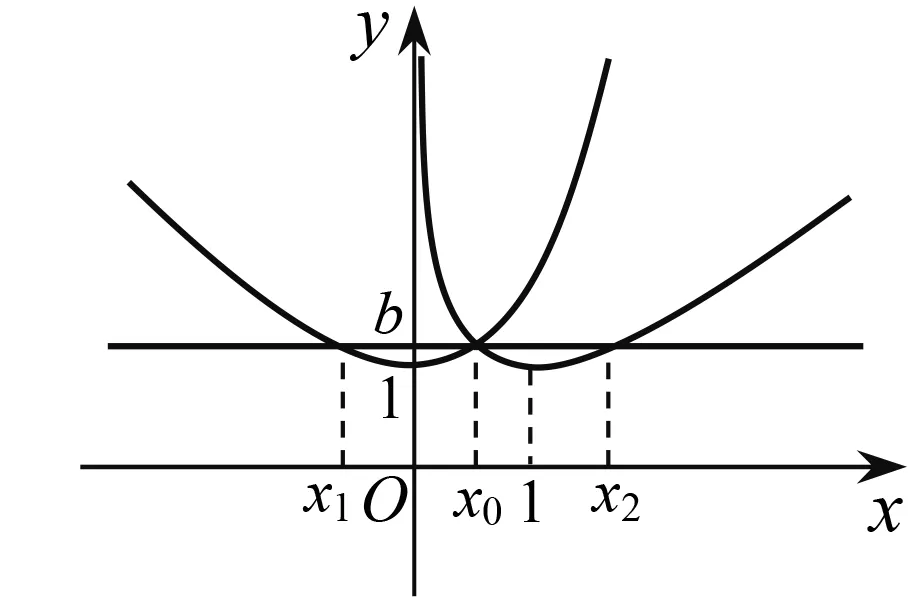
图1
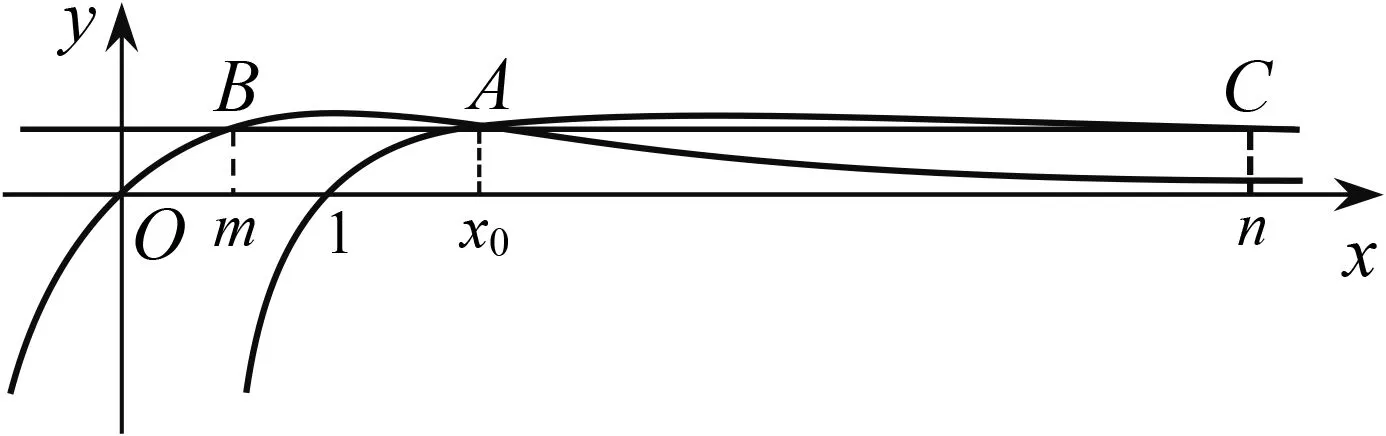
因为f(lnx0)=x0-lnx0=ex0-x0=f(x0),由f(x)的单调性可知,直线y=b与f(x)的图象交于两点(lnx0,b),(x0,b).因为g(ex0)=ex0-x0=x0-lnx0=g(x0),由g(x)的单调性可知,直线y=b与g(x)的图象交于两点(x0,b),(ex0,b),所以存在直线y=b与f(x),g(x)的图象有三个交点,其横坐标从左到右依次为lnx0,x0,ex0.由ex0-x0=x0-lnx0知,其横坐标成等差数列.
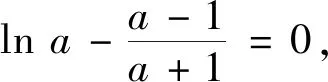
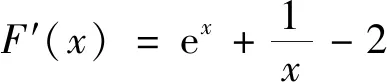
2 探究其他情况,得出一般结论
从上述分析可以发现,本题的第(2)题就是从直线y=b经过f(x)与g(x)图象的交点出发进行命制,考查了一种特殊情形.那么,对于一般情况,也就是直线y=b不经过f(x)与g(x)图象的交点时,是否有类似的结论?
变式1 已知直线y=b与f(x)=ex-x和g(x)=x-lnx的图象共有四个不同的交点.
(1)求实数b的取值范围;
(2)设这四个交点的横坐标从左到右依次为x1,x2,x3,x4,求证:x1+x4=x2+x3.
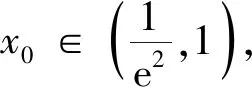
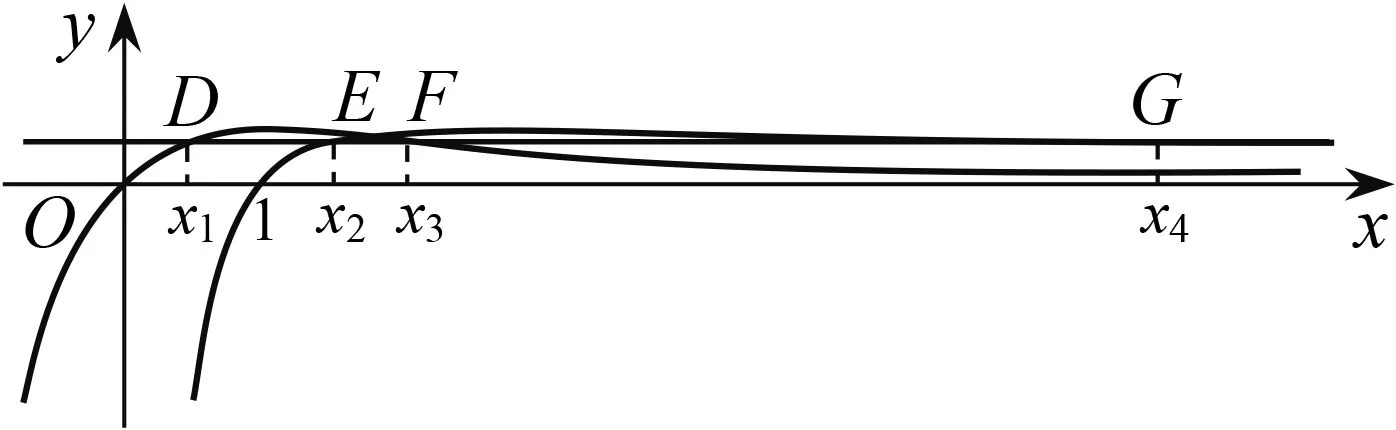
(2)①由(1)知,当b∈(1,y0)时,直线y=b与f(x)图象交点的横坐标从左到右依次为x1,x2,直线y=b与g(x)图象交点的横坐标从左到右依次为x3,x4,即f(x1)=f(x2)=g(x3)=g(x4)=b,其中lnx0 图2 图3 ②由(1)知,当b∈(y0,+∞)时,直线y=b与f(x)图象交点的横坐标从左到右依次为x1,x3,直线y=b与g(x)图象交点的横坐标从左到右依次为x2,x4,即f(x1)=g(x2)=f(x3)=g(x4)=b,其中x1 综上,x1+x4=x2+x3. 评注(1)对于变式1第(1)题中的交点个数问题,也可以用零点存在定理进行判断: (2)若将试题与变式1中的函数一般化,即f(x)=ax-x,g(x)=x-logax,其中a>1,容易判断f(x)与g(x)都只有一个极小值点,且极小值相等.利用f(logax)=g(x)与g(ax)=f(x)可以证明: ①若直线y=b与两条曲线y=f(x)和y=g(x)共有三个不同的交点,则从左到右的三个交点的横坐标成等差数列; ②若直线y=b与两条曲线y=f(x)和y=g(x)共有四个不同的交点,设这四个交点的横坐标从左到右依次为x1,x2,x3,x4,则x1+x4=x2+x3. 通过对试题与变式1的分析,我们发现函数f(x)与g(x)之所以具有上述性质,关键是满足两点:①f(logax)=g(x),g(ax)=f(x);②f(x)与g(x)都只有一个极值点,且极值相等. 下面笔者适当改变f(x)与g(x)的解析式,使其满足上述两个关键点,探究其他函数的类似性质. (1)若直线y=b与两条曲线y=f(x)和y=g(x)共有三个不同的交点,试探究:从左到右三个交点的横坐标之间的关系; (2)若直线y=b与两条曲线y=f(x)和y=g(x)共有四个不同的交点,试探究:从左到右四个交点的横坐标之间的关系. 放大延伸至建设工程全产业链上、全生命期管理上,还需要有更专业的合同管理、设备材料采购管理等进行配套,通过对工程数字化设计成果的充分利用,可以为“面向全产业链集成” 的工程数字化企业在今后必然会到来的生产任务的发展开创一个全新的业务领域,延长业务链条,增加新的赢利点。 图4 图5 综上,若直线y=b与两条曲线y=f(x)和y=g(x)共有四个不同的交点,设从左到右四个交点的横坐标分别为x1,x2,x3,x4,则x1x4=x2x3. ②当x∈(e,+∞)时,lnx>1,因为f(x)在(1,+∞)上递减,易证x>lnx,所以f(x) ①若直线y=b与两条曲线y=f(x)和y=g(x)共有三个不同的交点,则从左到右三个交点的横坐标成等比数列; ②若直线y=b与两条曲线y=f(x)和y=g(x)共有四个不同的交点,设这四个交点的横坐标从左到右依次为x1,x2,x3,x4,则x1x4=x2x3. 总之,对于一道典型的高考真题,我们不能仅仅局限于解决这个问题,还应从多个角度对其进行剖析,充分挖掘其价值.通常可以思考如下问题:你能用多种方法求解这个问题吗?这个问题的命题意图是什么?改变条件或目标后这些方法还适用吗?这个问题能否推广到一般情形?等等.只有真正弄清这个问题的来龙去脉,把握其各种变化,我们在遇到新问题时才能做到灵活处理、巧妙应对.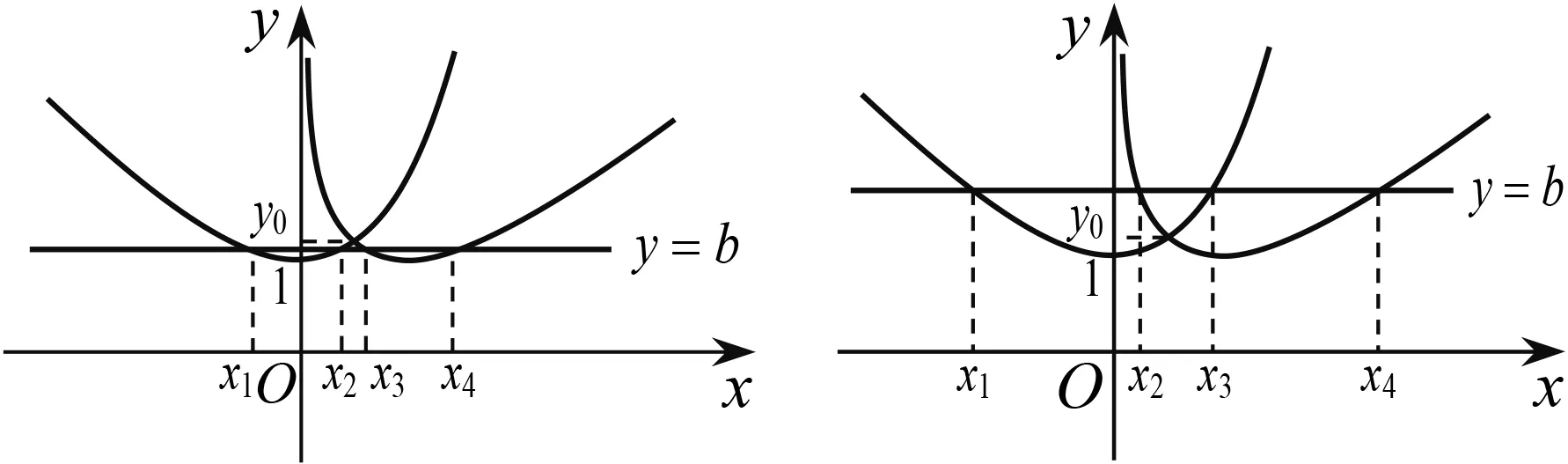
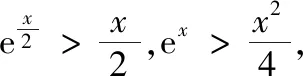
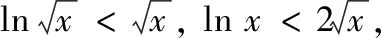
3 总结命题规律,探究其他性质
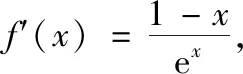
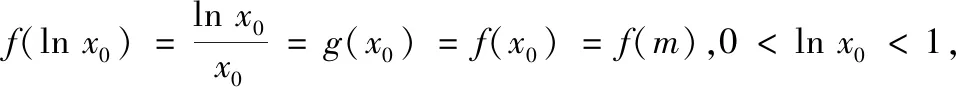

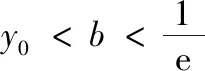
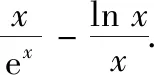

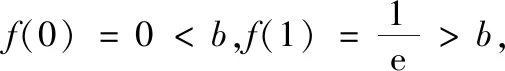
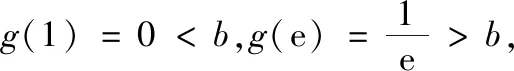
4 结语

