圆锥曲线对称问题“转化法”

甘肃省张掖市第二中学 纪相林

“圆锥曲线与方程”是湘教版选修(一)第2章的内容，虽然是选修内容，但其重要性却不容忽视.近几年来，“圆锥曲线对称问题”已成为高考中频繁出现的一个热点和难点问题.因此，熟悉这类问题的常见题型，掌握和运用“转化法”解题的方法与技巧也就显得十分重要[1].

圆锥曲线对称问题通常包括中心对称和轴对称两大类.对于中心对称类问题，一般采用“转化中点法”，利用中点坐标公式进行求解；对于轴对称类问题，一般采用“等价转化法”，将原问题转化为它的等价问题进行求解[2].

下面通过对典型例题的解析，来了解和掌握运用“转化”法来解决问题的方法与技巧.

1 转化中点法

一般情况下，对于中心对称类问题，主要根据“两对称点连线段被对称中心平分”这一性质，将其转化为中点问题进行解决.

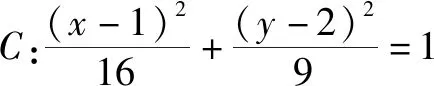
x′=-4-x，y′=2-y①

因为P′(x′,y′)在椭圆C上，所以

方法与技巧:本题属于曲线f(x,y)=0关于点Q(m,n)的对称曲线类典型问题.解决这类问题，首先将坐标平移，使原点移到对称中心Q，在新坐标系下原曲线为f(x′+m,y′+n)=0，其对称曲线为f(-x′+m,-y′+n)=0，然后再依据x′=x-m，y′=y-n将坐标系平移回原坐标系，可得到对称曲线的新方程f(2m-x,2n-y)=0，最后再把已知曲线方程中的x换成2m-x，y换成2n-y即可.

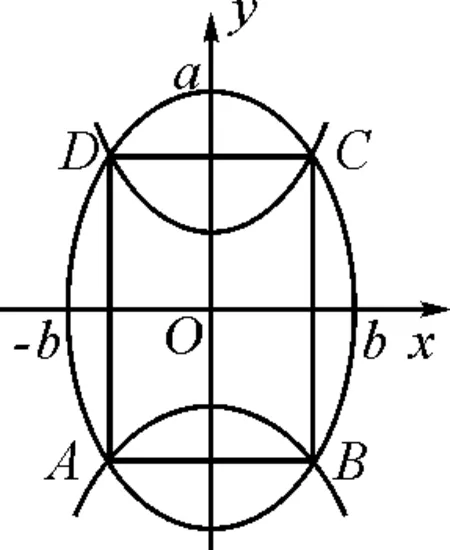
图1

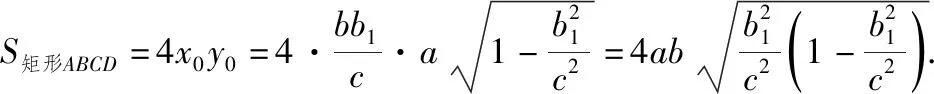
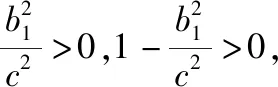
方法与技巧:在本题中，由于双曲线与椭圆有公共焦点，且有相同的对称轴，其四个交点组成以坐标轴为对称轴的矩形，我们只要研究在第一象限的情况即可解决问题.由此可见，对于一般的二次曲线问题，利用它转化为标准形式后的对称轴和对称中心来解决较为便捷[3].

2 等价转化法

对于求椭圆上存在两点关于某一条直线l对称类问题，我们可以化繁为简，将其转化为等价问题来解决.

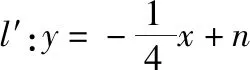
13x2-8nx+16n2-48=0

③

设l′与椭圆C的两个交点P(x1,y1)，Q(x2,y2)，显然x1≠x2.

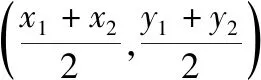
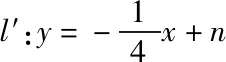
图2

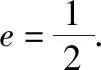
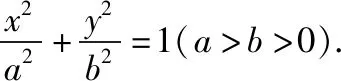
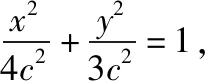
假设在E上存在关于直线l对称的两个不同的点B(x1，y1)和C(x2，y2).

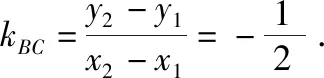
设BC的中点为M(x0，y0)，则

因为点M在直线l上，所以

2x0-y0-1=0 ④

3x0-2y0=0 ⑤

④×2-⑤,得x0=2.这表明BC的中点就是点A,当然这是不可能的.也就是说，椭圆E上不存在关于直线l对称的相异两点.

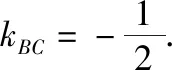
方法与技巧:本题仍然是采用将待证点B，C等价转换为已知点A的间接证明思路.在具体证明过程中，首先根据已知条件求出椭圆方程，然后利用椭圆的方程、性质和已知直线的斜率得出假设的BC中点的坐标与椭圆E上的点A重合的反面结论，从而使原题得证.

从上述典型例题的方法与技巧的总结中，我们可以看出，运用“转化法”解决圆锥曲线对称问题具有较强的可行性与实用性，关键是要充分、灵活地利用好椭圆、直线与点的相关性质.