基于用户用电行为预测的需求侧负荷调控

马爽，王绎

(1.北京信息科技大学 自动化学院，北京 100192；2.中国电建集团昆明勘测设计研究院有限公司，昆明 650051)

0 引言

风力和光伏的大规模接入为电力系统提供了更多的清洁能源形式，但可再生能源的随机性和波动性也为电网的安全稳定运行带来了新的挑战。随着智能电表的普及和科技的发展，需求侧的可控负荷资源为电力系统削峰填谷和新能源消纳等提供了新的解决方案[1]。然而，用户的用电行为具有复杂性和多样性[2]，在一定程度上影响了负荷调控效果。在先进量测技术和数据管理技术的基础上，利用负荷数据研究用户的用电规律并预测用户用电行为随时间的变化趋势，建立合理的需求侧负荷调控机制，对于节约响应成本和促进可再生能源消纳具有重要意义。

目前，已有学者针对需求侧电力用户用电行为展开研究。文献[3]建立了基于分时电价的用户可调节潜力指标，基于负荷的调节潜力大小对用户的用电行为进行聚类分析。文献[4]在分析居民用户基本负荷、可调度负荷、电动汽车负荷和储能负荷的基础上，以电网负荷波动最小为调控目标建立需求侧响应模型，并通过对用户侧用电行为的聚类分析求解调控结果。文献[5-6]通过分析用户用电行为的多维影响因素，提出了融合K-means和自组织竞争神经网络的用户可调节潜力的二次聚类方法，实现基于负荷特性的可调节潜力综合聚类。类似地，文献[7-8]将无监督极限学习机和主成分分析用于用户用电行为分析，针对用电行为的复杂性、随机性和不确定性，对用电负荷数据进行聚类，得到不同的用电模式。整体而言，目前的研究大多以居民的静态负荷数据为基础，通过对历史负荷数据的聚类分析得到各时段的可调控负荷潜力或居民用电模式。但是电力负荷数据本质上是一种随时间推移而观测到的时间序列值，具有典型的趋势性、季节性和周期性等，负荷用户用电行为的时间尺度特征需要进一步挖掘。

在需求侧负荷调控策略方面，文献[9]以电热水器为对象，研究了面向新能源消纳的聚合负荷协同控制策略，在建立热水器负荷控制模型的基础上，从状态感知、实时分析、科学决策和精准执行4个环节进行负荷控制，实现了电网的供需平衡调节。为降低不确定性对负荷调控的影响，文献[10]从时间角度描述了影响负荷调控的不确定性因素，建立了考虑鲁棒性与经济性的电热水器调控两阶段优化模型，在不确定集合的约束下实现对新能源的精准消纳。文献[11]融合了中央空调的调控特性、居民舒适度和用电经济性等多方因素，提出了3种中央空调负荷聚合策略，并研究了聚合负荷参与平抑分布式电源出力的性能。文献[12]通过分析居民用户对电热水器和中央空调的使用习惯，提出一种考虑时域特性的异构温控负荷联合调控策略，使负荷的使用时段与风电出力尽可能匹配。现有研究针对需求侧的负荷调控取得了较好的效果，但用户负荷时间序列的随机性和规律性对负荷调控的影响仍需要深入研究。在面向新能源消纳时，较少考虑可调节负荷序列与新能源发电出力序列之间的趋势相关性。

综上所述，本文以新能源消纳为研究场景，针对用户用电行为的日周期性和周周期性，提出基于时间序列预测的用电行为分析和需求侧负荷调控策略。在分析用户历史负荷序列的基础上，采用双周期季节性差分自回归移动平均模型预测用户可调控负荷的时域使用行为。从用户负荷功率与风力发电出力的时序关联度出发设置调控优先级，实现用户可转移负荷参与新能源消纳的有序调控。

1 用户用电行为时间序列预测

居民用户可参与需求侧互动的负荷主要包括可削减负荷和可转移负荷两类。可削减负荷为在不影响用户舒适度的情况下可削减的部分负荷量，如：空调、智能电子设备等；可转移负荷则为在规定的时间段内满足用电需求即可的负荷，如热水器、洗碗机、电动汽车等[13]。为了最大程度地减少需求侧调控对居民用电的限制，本文只针对热水器和电动汽车两种可转移负荷展开研究，不削减用户的总用电量，并假设在智能电表和非入侵式探测技术的帮助下，可以获取居民家庭每种电器的负荷序列。

用户负荷虽然随时间波动，但也表现出与居民行为习惯强相关的周期性，例如电热水器的使用与用户的洗浴行为有关，其使用时段相对集中在早晨及晚上。根据2015 年深圳市夏季典型负荷曲线[14]，居民用户的负荷具有明显的日周期性和周周期性，工作日和周末也可以明显被区分开。借鉴文献[15]的交通流预测模型，本文采用双周期季节性差分自回归移动平均(double seasonal autoregressive integrated moving average，DSARIMA)模型实现对居民用户可转移负荷使用行为的预测。差分自回归移动平均(autoregressive integrated moving average，ARIMA)模型的基本思想为将预测对象随时间推移而形成的数据序列描述为一个随机序列，再依据时间序列的过去值及现在值预测未来值。DSARIMA模型则在ARIMA模型的基础上考虑了时间序列的周期性，在模型中采用了一个以天为单位的短季节周期和一个以周为单位的长季节周期，如式(1)所示：

φ(B)φ(BSS)φ(BSL)(1-B)d(1-B)DS(1-B)DLxt=

C+θ(B)θ(BSS)θ(BSL)εt

(1)

式中：xt为可转移负荷的时间序列；B为后移算子，满足Bnxt=xt-n；d为差分次数；SS和SL分别为短季节和长季节周期的长度；DS和DL分别为短季节和长季节差分次数；BSS和BSL分别为短季节和长季节周期的后移算子；φ(B)和θ(B)分别为ARIMA模型的自回归系数多项式和移动平滑系数多项式；C为常数；εt为残差项。

φ(BSS)=1-φ1BSS，1-φ2BSS,2…-φPSBSS,PS为短季节模型的自回归系数多项式；θ(BSS)=1-θ1BSS，1-θ2BSS,2…-θQSBSS,QS为短季节模型的移动平滑系数多项式；φ(BSL)=1-φ1BSL，1-φ2BSL,2…-φPLBSL,PL为长季节模型的自回归系数多项式；θ(BSL)=1-θ1BSL，1-θ2BSL,2…-θQLBSL,QL为长季节模型的移动平滑系数多项式；其中PS和PL分别为短季节和长季节周期自回归(seasonal autoregressive，SAR)项的滞后阶数，QS和QL分别为短季节和长季节周期移动平均(seasonal moving average，SMR)项的滞后阶数。

DSARIMA模型同时考虑了两个周期的时间序列预测，符合居民用户在工作日和周末具有不同用电行为的特定规律。基于DSARIMA模型的用户负荷时间序列预测将每周划分为工作日(周一到周五)与非工作日(周六与周日)两个周期，并将每天划分为n个时段，将当前预测时间段的前Z天(同为工作日或非工作日)同一时间段的负荷构建为时间序列，分别预测两类日期中各时段的热水器和电动汽车负荷，以描述用户在不同时段对两类电器的使用行为，具体流程为：

1)采用自相关图法对所选取的热水器和电动汽车负荷序列的平稳性进行检验，并通过差分运算处理不平稳的序列，确定差分次数d、DS和DL；

2)根据最小信息量准则确定模型阶数PS、QS、PL和QL；

3)采用最大似然估计法对DSARIMA模型进行参数估计，确定φ和θ值；

4)对参数确定后的模型进行残差检验，确定检验结果呈现随机正态分布且不自相关；

5)利用最终确定的模型进行热水器和电动汽车负荷序列预测并得出结果。

2 面向风电出力消纳的负荷有序调控

本文所提出的面向风电出力消纳的需求侧负荷调控架构如图1所示，假设风电出力信息可由电网侧获取，通过对各个时间段内可转移负荷的有序调控，实现对目标风力发电的消纳。具体描述为：

1)电网调度中心根据风力发电出力的历史数据等信息，确定各个时段需要消纳的风力发电量，作为待消纳的已知目标量下发给聚合商；

2)聚合商提前与参与风电消纳的用户签订合同，并获取用户对于电热水器和电动汽车的负荷可允许转移时间约束；

3)聚合商根据所采集的用户负荷历史数据，分别构建工作日和非工作日的负荷时间序列，采用DSARIMA模型预测消纳时段内用户对电热水器和电动汽车负荷的用电行为；

4)在消纳时段，聚合商根据用户可转移负荷的响应容量与风电出力的差异和时序相关度等，确定用户的调控优先级及各时段内的调控量，实现负荷有序调控。

为了跟踪风电出力，确保各个时间段内取得良好的新能源消纳效果，本文以各时间段内风电出力功率与需求侧负荷聚合功率之间的偏差最小为目标函数，如式(2)所示。

(2)

针对上述调控目标与约束，按照负荷优先级划分的调控方法，实现对各时间段内用户负荷的有序调度。各时段可聚合的负荷功率为

(3)

式中：p1,j和p2,j分别为参与消纳的电热水器和电动汽车的固定功率；μ1,j和μ2,j分别为参与消纳的电热水器和电动汽车的调控因子；M和N分别为参与消纳的电热水器和电动汽车的数量。

用户可转移负荷的调控因子如式(4)和式(5)所示，只有当调控时间处于用户允许的时间范围内才可参与需求侧响应。

(4)

(5)

式中：T1,j和T2,j分别为电热水器和电动汽车的负荷可允许转移时间段。

负荷调控优先级同时受到用户使用习惯、用户行为预测结果和风电出力的影响。为了最大程度地降低负荷调控对用户舒适度和用电习惯的影响，本文根据式(6)确定各时段电热水器和电动汽车的负荷调控优先级：

(6)

式中：γi,j表示i时间段内第j个参与消纳的负荷(电热水器或电动汽车)的负荷时间序列预测值与风电出力功率之间的皮尔逊相关度，具体计算方法可参考文献[16]。λi,j取值范围为[0,1]且与γi,j呈正相关，以确保各时段内与风电出力功率变化趋势相似性最高的负荷优先参与消纳，同时减少对用户电器使用习惯的影响。在负荷调控过程中，按照λi,j确定各类负荷的调控顺序。

3 算例分析

以某住宅区域用户夏季某一工作日/非工作日的用电情况为例，调控时段为该日0点至24点，将1天划分为48个时段，每个时段30 min。以预测日前50 d的历史负荷数据作为样本集，其中工作日35 d，非工作日15 d，分别预测下一个工作日/非工作日的用户负荷功率情况，算例仿真平台为Matlab。

对于下一个工作日的每一个时段，采集该时段前35 d同一时段的数据和该时段前24个时段的数据，依据DSARIMA模型采用1阶差分进行预测，得到第36个工作日的负荷数据。同样地，对于下一个非工作日的每一个时段，采集同样的方法得到第16个非工作日的负荷数据。分别采用基本ARIMA模型和DSARIMA模型预测负荷时间序列，差分阶数均为1。在负荷历史数据时间序列的基础上，根据最小信息量准则确定模型参数PS、QS、PL和QL分别为7、7、4、6，并依据绝对平均误差(mean absolute error，MAE)和均方根误差(root mean square error，RMSE)评价预测性能，结果如表1所示。

表1 负荷时间序列预测结果分析 kW

从表1可以看出，采用DSARIMA模型进行负荷时间序列预测时，在工作日和非工作日都取得了更好的效果，从而说明用户用电在工作日和非工作日都呈现一定的规律性和周期性，而DSARIMA模型能够更好地捕捉用户行为在不同时期的变化趋势。

图2为采用DSARIMA模型对某一用户工作日负荷的预测结果与真实负荷数据的对比图。由图2可知，负荷时间序列的预测值能够较为准确地刻画用户对家用电器的使用习惯，为需求侧负荷的有序调控奠定了基础。

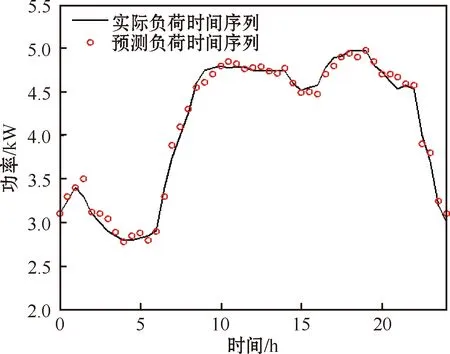
图2 基于DSARIMA模型的负荷序列预测结果

为了验证本文面向风电出力消纳的负荷有序调控策略的可行性，以我国西部地区某风电场一天的实际风电出力曲线作为消纳目标，如图3中的蓝色实线所示。需求侧电热水器和电动汽车的相关参数设置如表2所示，分别采用本文算法和文献[12]的贝叶斯网络模型预测用户的用电行为，并分析负荷参与风电出力消纳的效果，结果如图3所示。

表2 可转移负荷参数设置

图3 风电消纳效果对比分析

由图3对比结果可知，本文策略在全天均取得更好的消纳效果，受居民用户的用电习惯影响，当深夜风电出力功率较大时，参与需求侧调控的可转移负荷功率略显不足。本文的调控策略从用户用电习惯分析及其与新能源发电出力的相关性出发，在负荷可转移时间的约束下，优先聚合各时段内与风电出力功率变化趋势相似的负荷，从而在很大程度上避免需求侧调控对用户正常用电带来的影响，提升新能源消纳效果与能源利用效率。

4 结束语

本文以新能源消纳为应用场景，研究了基于负荷时间序列预测的用户用电行为分析和需求侧负荷有序调控方法。针对用户负荷使用习惯在工作日和非工作日呈现出的周期性，采用DSARIMA模型预测各个时间段的用户可转移负荷序列。以负荷功率与风力发电出力的差异性作为消纳目标函数，以二者的时序相关性指导负荷有序参与需求侧新能源消纳。本文的研究方法可适用于居民家用负荷参与电网负荷调峰、新能源消纳等场景，下一步将重点研究包含电力负荷在内的需求侧综合能源调控。