随机不确定时延Markov系统鲁棒容错控制及应用

付兴建，吕永霞，严航

(北京信息科技大学 自动化学院，北京 100192)

0 引言

容错控制是当电子控制系统的传感器、执行器等部件出现故障时仍能保持系统性能的一种方法。设计鲁棒容错控制系统时，需要同时考虑系统故障、建模误差和外界干扰等不确定因素的影响[1-3]。当前容错控制系统的研究集中在设计合适的控制机制，解决系统执行器、传感器、系统本身和关联链接等机构各类故障的自动补偿和抑制，以及不同故障模式下的性能优化问题[4-6]。随着高精尖技术的发展，鲁棒容错控制有很广泛的应用前景。

Markov系统是一类包含连续时间状态变量和离散时间模态变量的混杂系统或随机系统，可用于描述受随机突变和环境变化影响的系统，这与网络控制系统的特性比较一致。Markov系统主要由两部分组成，其中一部分是Markov的跳变参数模态，通过从有限个离散事件的集合中选取得到；另一部分是系统的状态变量，它是随时间而变化的量。Markov系统可以用来描述广泛的实际系统，包括航空航天系统、制造系统、电力系统和无人机编队系统等[7-8]。特别地，由于元器件故障或外界的环境变化、网络延迟等随机突变现象，系统发生结构或者参数上的突然变化，这时系统往往可以抽象为Markov跳变系统模型进行建模和分析。近年来，Markov系统的研究成为热点，主要研究包括稳定性与控制设计、故障检测与容错控制等[9-11]。

本文针对具有随机不确定时延的Markov网络系统，对系统自身存在的各种元器件故障和外界扰动的情况进行分析，给出了故障模型；考虑双网络时延，设计了依赖网络时延的状态反馈控制器；基于Lyapunov稳定理论，研究了随机Markov系统在执行器故障和扰动情况下的鲁棒容错控制。对系统中存在不同特性的传感器故障，给出了鲁棒容错控制律存在的条件，使得闭环系统渐近稳定并且满足一定的干扰抑制水平，保证了随机不确定时延的Markov网络系统的稳定性和可靠性，降低了系统对故障的敏感度。最后，通过应用仿真，将所提出的方法应用于四旋翼无人机姿态系统，仿真了系统在干扰和故障发生后，其姿态的响应变化曲线，验证了容错控制方法的有效性。

1 故障建模

故障建模针对如下系统：

(1)

式中：x(t)为系统状态向量；y(t)为输出；ε(t)为外部扰动;A、B、C、D是适当维数的常数矩阵。

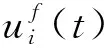
i=1,2,…,m

(2)

定义：

(I-ρ(t))u(t)+Ω(t)

(3)

其中：

ρ(t)=diag{ρ1(t)ρ2(t) …ρm(t)}

Ω(t)=diag{Ω1(t)Ω2(t) …Ωm(t)}

式中I为适当维数的单位矩阵。

现对系统作如下假设。

假设1：系统内的所有状态都是能观测的。

假设2：在执行器故障下，系统是能控的。

则结合故障情况的状态空间表达式，有：

(4)

2 Markov系统鲁棒容错控制器设计

2.1 问题描述

假设τ1(t)表示系统传感器到其控制器的网络时延；τ2(t)表示系统控制器到目标执行器的网络时延。假设τ1(t)、τ2(t)为任意随机的Markov链，记为τ1(η1(t))、τ2(η2(t))。其中，η1(t)、η2(t)是连续时间的Markov随机过程，分别表示网络时延τ1(t)和τ2(t)的模态，并且相应的有限状态集合分别为S1={1,2,…,N1}和S2={1,2,…,N2}，而η1(t)所对应的转移概率矩阵为

(5)

(6)

假设所考虑的系统状态是可观测的，则可设计如下的依赖网络时延的状态反馈控制器：

uT(t)=Kx{t-τ1[η1(t)]-τ2[η2(t)]}

(7)

式中：uT(t)为到达执行器端的控制输入；K为待求的鲁棒容错控制器；η1(t)∈S1,η2(t)∈S2。

考虑时延、不确定性以及外部干扰ε(t)，可把系统(1)写为如下形式：

(8)

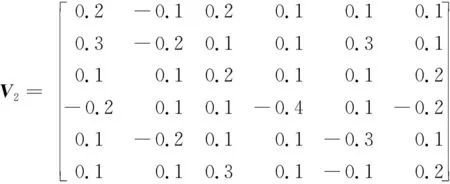
[ΔAΔB]=HF(t)[V1V2]

(9)

式中：H、V1、V2为适当维数的实常数矩阵。

2.2 鲁棒容错控制器设计

在给出本文主要结论之前，先给出如下定义和引理。

(10)

成立，则称系统是约束条件下稳定的。

定义2在零初始条件下，假定γ>0，对于任意非零外部扰动输入ε(t)∈L2[0,∞)，若满足

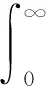
(11)

则称由式(7)和式(8)组成的闭环系统满足H∞性能γ。

引理[12]给定适当维数矩阵Y=YT和矩阵R1、R2，则

(12)

对所有满足Σ(t)TΣ(t)≤I的矩阵Σ(t)成立，当且仅当存在一个常数κ>0，使得：

(13)

接下来，给出在鲁棒容错控制器作用下，随机不确定时延Markov系统稳定的条件。

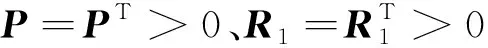
(14)

其中：

Π22=-R1-R2，Π42=B(I-ρ(t))K，Π43=BΩ，

Π51=R2A，Π52=R2B(I-ρ(t))K，Π61=V1P则闭环系统是稳定的，并且具有H∞性能。式中*表示矩阵的对称转置部分。

证明定义随机过程{x(t),τ1(η1t),τ2(η2t)}，其中x(t)=x(t+s)，s∈[-τ1(η1t)-τ2(η2t),0]，另外，η1t和η2t分别表示η1(t)和η2(t)，则可得该随机过程为强Markov过程。构造Lyapunov泛函：

V(xt,η1t,η2t)=V0(xt,η1t,η2t)+

V1(xt,η1t,η2t)+V2(xt,η1t,η2t)

(15)

式中：

V0(xt,η1t,η2t)=xT(t)Px(t)

(16)

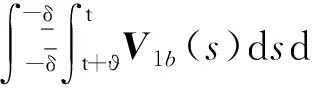
(17)

其中：

(18)

其中：

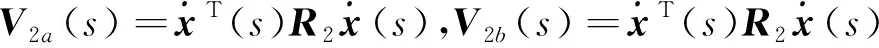
ΔV(xt,a,b)≤

xT(t)HTP(a,b)(Ax(t) +B(I-ρ(t))Kx(t-

τ1(a)-τ2(b))) +(Ax(t)+B(I-ρ(t)Kx(t-

τ1(a)-τ2(b)))TP(a,b)Hx(t) +

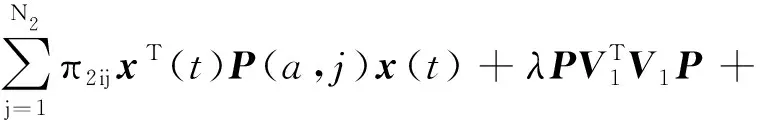
τ2(η2))R1x(t-τ1(η1)-τ2(η2)) +

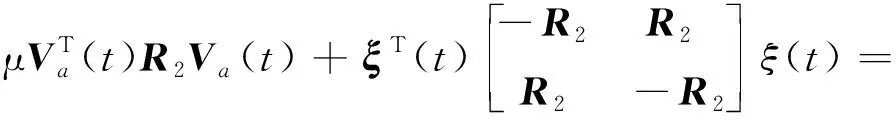
ξT(t)Ν(a,b)ξ(t)

(19)

其中：

ξT(t)=[xT(t)xT(t-τ1(a)-τ2(b))]；

Va(t)=Ax(t)+B(I-ρ(t))Kx(t-

τ1(a)-τ2(b))；

N(a,b)=

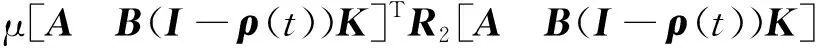
(20)

根据Schur补引理，结合式(14)可得N(a,b)<0。

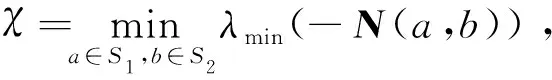
[V(x(T),η1(T),η2(T))]-[V(x0,η10,η20)]=

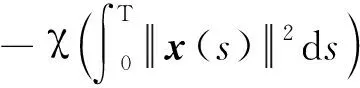
(21)

当T→∞时，对上述不等式两端取极限，可得：

(22)

Ψ(Φ,η10,η20)

(23)

根据定义1，闭环系统是稳定的。

下面证明系统满足H∞性能。根据以上证明，有：

ΔV(xt,a,b)≤ζT(t)Ξ1(a,b)ζ(t)

(24)

式中：ζ(t)=[ξT(t)εT(t)]T

Ξ1(a,b)=

对如下泛函指标：

(25)

在零初始条件下则有：

V(x0,η10,η20)=0，V(x(∞),η1(∞),η2(∞))≥0

(26)

可得：

J=

V(x(∞),η1(∞),η2(∞))≤

(27)

将式(25)代入(29)可得：

γ-1zT(t)z(t)-γεT(t)ε(t)+ΔV(xt,t,a,b)≤

ξT(t)γ-1CTCξ(t)-γεT(t)ε(t)+

ζT(t)Ξ1(a,b)ζ(t)≤ζT(t)Ξ2(a,b)ζ(t)

(28)

式中：

Ξ2(a,b)=

μ[ABK]TR2[ABK]+γ-1CTC

再结合Schur补引理，对于所有的ε(t)∈L2[0 ∞)，当ζ(t)≠0时，即有

(29)

根据定义2，系统满足H∞性能。

3 应用仿真研究

在四旋翼无人机姿态控制系统中，由于控制系统可能会存在元器件故障或外界环境变化等随机突变现象，这时，姿态控制系统可以抽象为Markov系统模型进行建模和分析。

本文以某种四旋翼无人机[13]为例，对所提出的具有随机不确定时延Markov网络系统的鲁棒容错控制进行应用仿真研究。

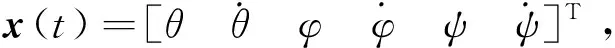
其中：

为简便，假设转移概率矩阵为

其他参数选取：时延τ1(t)=0.1sint；τ2(t)=0.2cost；F(t)=0.1sint。

在无故障和扰动情况下，取Ωi=0，ρ=0。由(14)式可解得

K=

此时，俯仰角、滚转角和偏航角姿态变化，如图1～3所示。可看出，系统在无故障情况下，能快速达到稳定。

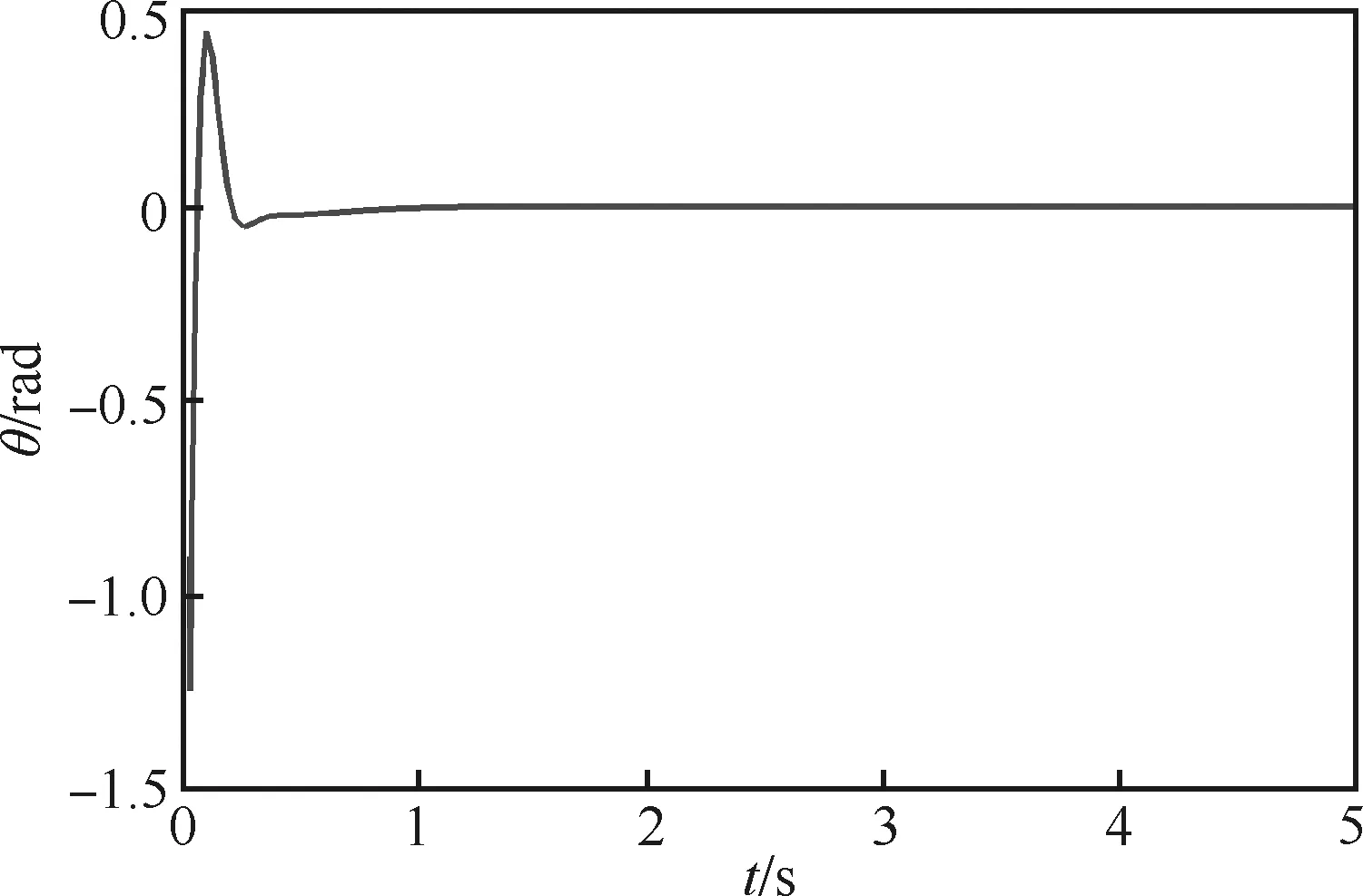
图1 俯仰角曲线

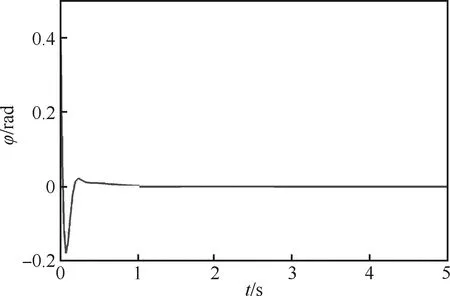
图2 滚转角曲线

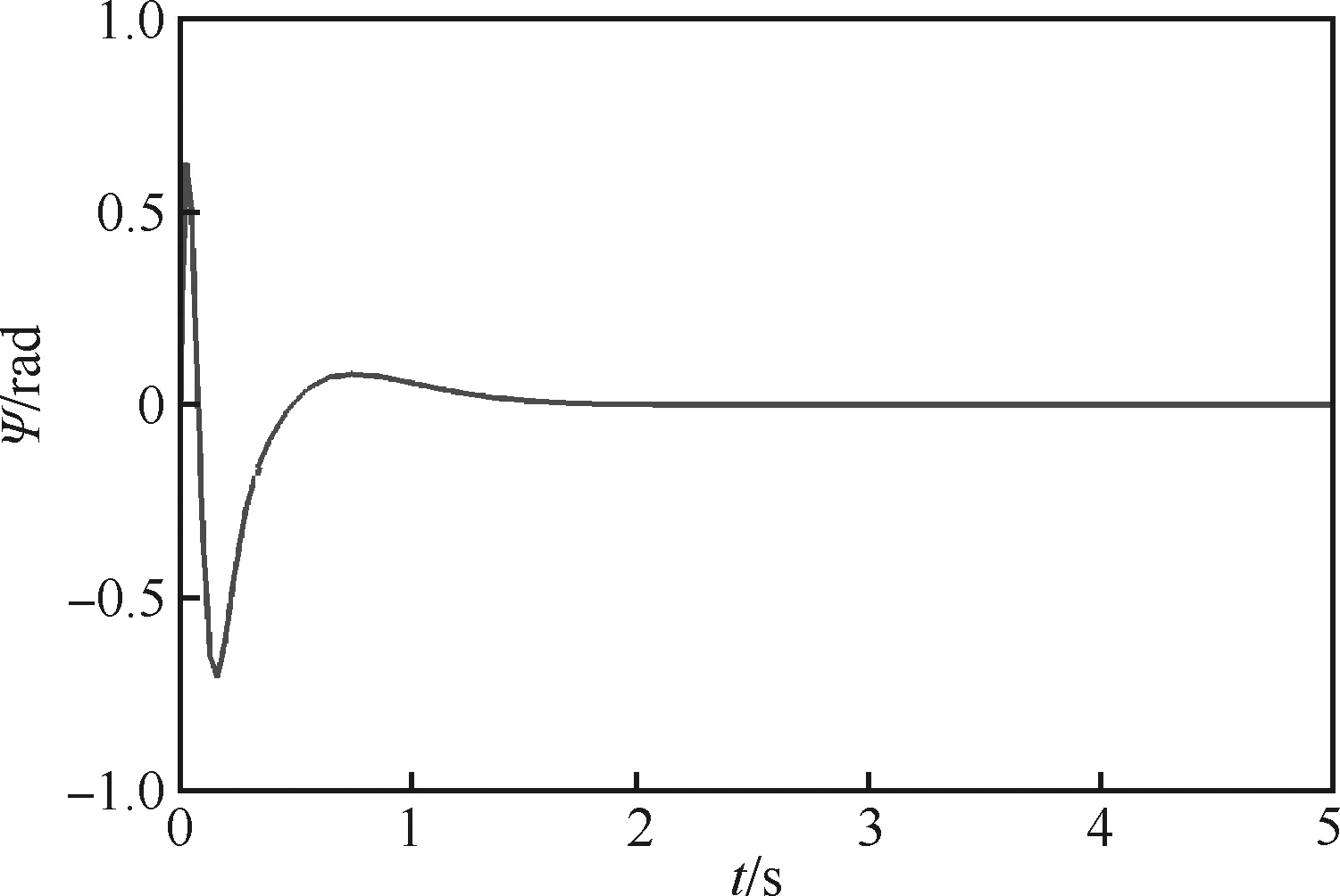
图3 偏航角曲线

K=

则无人机的俯仰角、滚转角、偏航角曲线变化，如图4～6所示。

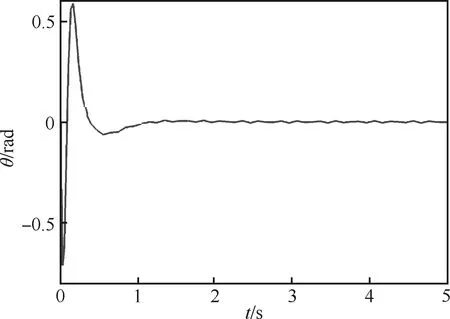
图4 故障时俯仰角曲线

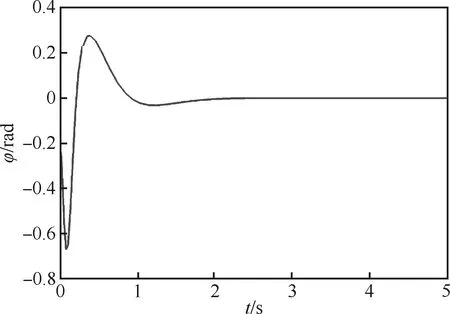
图5 故障时滚转角曲线

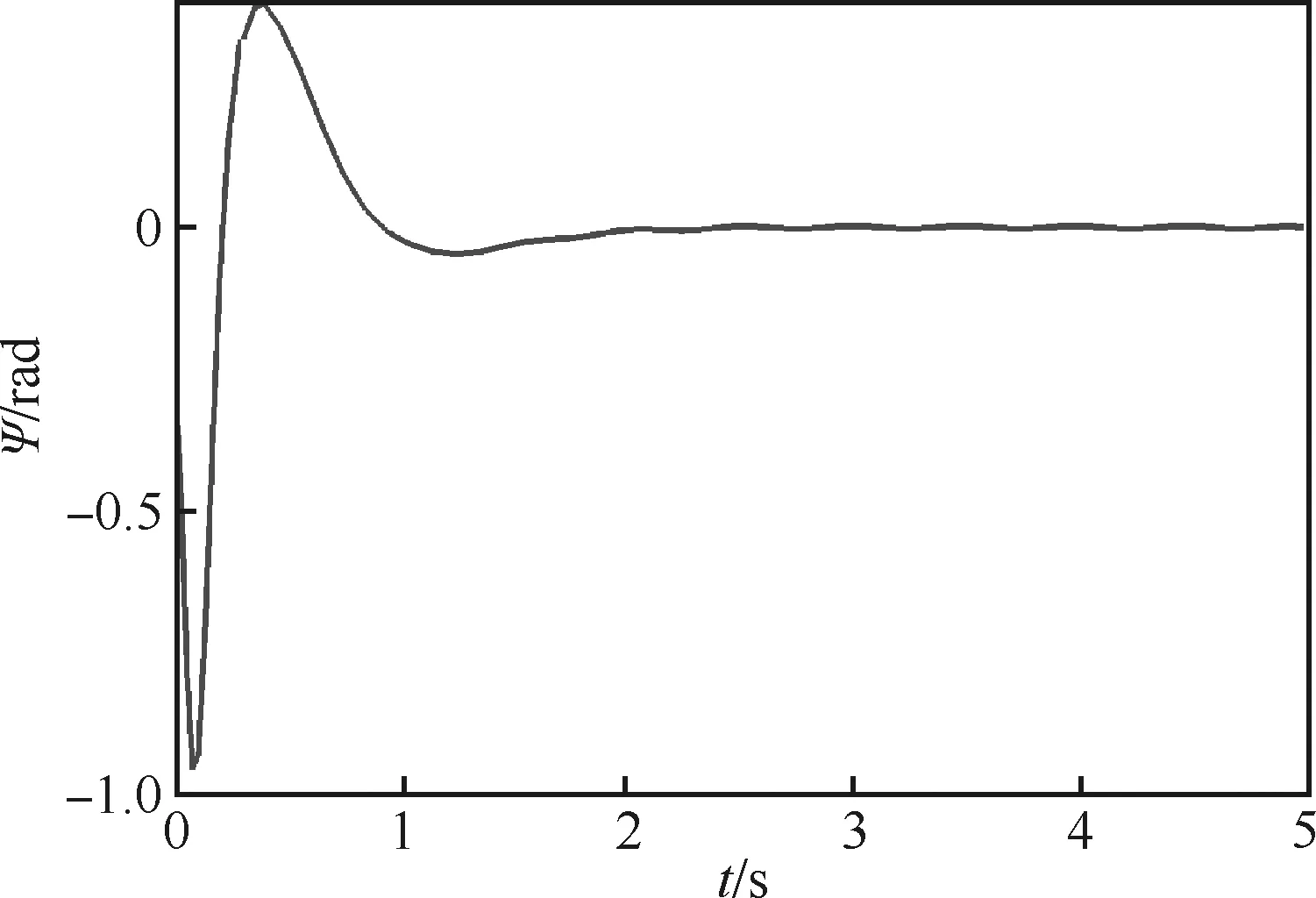
图6 故障时偏航角曲线

从仿真结果图4～6看出，无人机在干扰和故障发生后能渐近恢复至稳定状态，表明加入外部扰动和故障时，系统能快速检测到发生故障，调用相应的控制策略，实现对故障的有效容错控制，保证无人机在执行器部分失效的情况下仍能稳定，确保了无人机安全可靠运行，验证了设计的鲁棒容错控制器的有效性。

4 结束语

本文以随机不确定时延Markov网络系统为对象，研究了系统发生执行器故障和受到外界干扰时的鲁棒容错控制。以Lyapunov理论为基础，设计了依赖网络时延的鲁棒容错控制器，给出了网络系统鲁棒容错控制器存在的条件。最后，进行了无人机应用仿真研究，验证了鲁棒容错控制器的有效性。

本文只是研究了转移概率已知情形下Markov网络系统的鲁棒容错控制问题，对于转移概率部分未知和完全未知情形下的Markov系统的稳定性和鲁棒容错控制问题还需要进一步的探讨。