焊接机器人用永磁同步电机电流预测控制＊

林立 ，窦威龙 ，林敏之

（1．多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳 422000；2．邵阳学院电气工程学院，湖南 邵阳 422000；3．邵阳资水科技有限公司，湖南 邵阳 422000）

焊接机器人具有工作效率高、焊接质量好、灵活可靠等特点，在汽车行业、电子行业、船舶行业等得到了广泛的应用[1]。永磁同步电机（PMSM）凭借结构简单、可靠性高、效率高等特点被广泛应用于焊接机器人控制领域[2－4]。而传统控制策略例如PI控制，在实际控制中易造成系统超调和振荡问题，难以满足焊接机器人高性能的控制需求。近年来，预测控制因其动态响应好、谐波分量小的优势得到广泛应用。

在预测控制中，无差拍电流预测控制（DPCC）由PMSM离散化模型将当前周期电流给定值作为下一周期电流预测值，能准确计算出控制电压，从而实现无差拍跟踪控制[5]。而模型预测控制（MPC）通过预设判据优化未来动作，控制灵活且对系统变量的约束能力强，已成为众多学者研究的热点[6]。

本文根据PMSM在同步旋转坐标系下的非线性离散数学模型推导出DPCC模型，由PMSM转矩方程与运动方程推导出MPC模型，提出一种改进无差拍电流预测控制与模型预测控制相结合的预测控制方法。通过仿真及实验表明了本文所提方法相较于传统PI矢量控制，有效提高了系统的动态响应能力及抗负载干扰能力，且实现转速无超调。

1 模型预测控制器分析设计

由于机械模型需要负载转矩才能准确估计速度，根据系统控制要求，设计一种模型预测控制器。当电机为表贴式永磁同步电机时：Ld＝Lq＝L，且采用id＝0的控制方法，则电磁转矩方程可变为

运动方程为

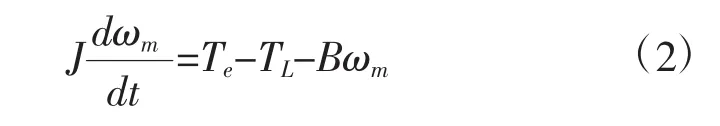
将转矩方程与运动方程相结合得如下：

其中，ωm为电机的机械角速度，J为转动惯量，B为阻尼系数，TL为负载转矩，Te为电磁转矩，iq是定子电流q轴分量，ψf为电机永磁体的额定磁链。

对式（3）推导求解，当负载转矩在采样时间内不变时，最后获得正交定子电流参考值：

其中，ω1和iqref分别为给定机械速度和正交电流参考值。

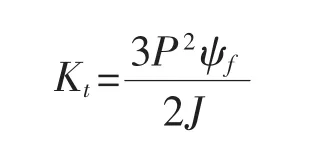
2 改进型无差拍电流预测控制器设计

永磁同步电机在d－q轴坐标系下的定子电压方程为

式中：ud，uq，id，iq分别是定子电压、电流 d－q 轴分量，R为定子电阻，ωe为电角度，LdLq是直轴电感、交轴电感。

采用一阶泰勒公式法对式（5）进行离散化，由于控制系统中采样时间Ts非常的短，即可得：

可改写成如下形式：

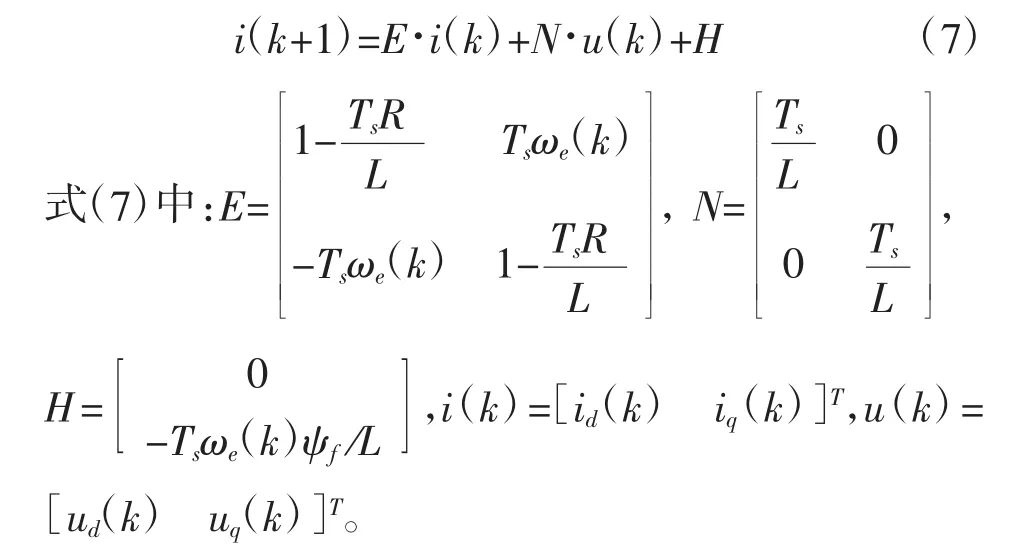
由传统DPCC控制原理可知，要想实现系统的实际输出电流值能够无差拍的对电流参考值进行跟踪，则有参考电流值 idref，iqref作为下一时刻 T（k＋1）的电机电流值i（dk＋1），i（qk＋1），就可以算出Tk时刻所需的最优电压空间矢量，当采样周期的时间足够短时（本文采样周期为0．00001s），就可以认为电机的电流i（dk＋1），i（qk＋1）无差拍跟踪参考电流值idref，iqref，从而实现电流环的快速响应控制。由此得到当前时刻控制器的输出为：

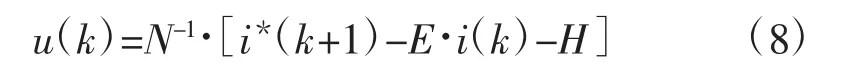
式（8）中：i＊（k＋1）为电流参考值，i＊（k＋1）＝[idrefiqre]fT。

理论上实际采样电流可以在一个采样周期后跟随上电流参考值，但在实际的控制系统中，受到电流采样，脉宽调制等延时环节的影响。可知采样电流值i（dk＋2），i（qk＋2）在第k＋2个周期才能跟踪上电流参考值i＊（k＋1），本文采用带预测电流误差校正环节的两步预测法。

由式（8）知第k＋1时刻电压值为：

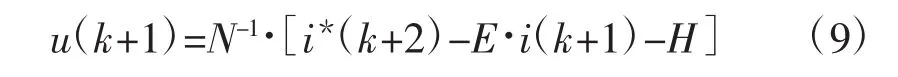
由式（7）知：

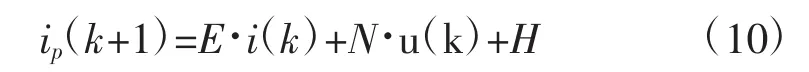
式中：ip（k＋1）为第k＋1时刻电流预测值。将ip（k＋1）代替式（9）中的i（k＋1）可得两步预测后的电压值

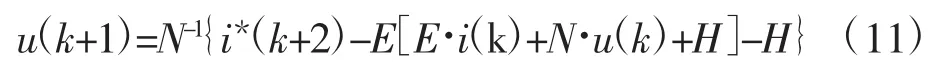
式（11）直接使用ip（k＋1）代替的i（k＋1），会使系统造成较大预测误差，降低电流跟踪精度，因此引入电流校正环节来抑制电流跟踪误差，即：

式（12）中：ie（k）＝ip（k＋1）－i（k＋1），K为电流误差校正因子。

综上可得改进后DPCC算法的电压指令值：

3 仿真结果及分析

为验证本文所提控制策略的可行性与有效性，搭建了PMSM电流预测控制系统仿真模型，结构框图如图1所示，PMSM参数为：额定功率PN＝0．75kW，额定转矩 TN＝2．39N·m，极对数 P＝4，交直轴电感 Ld＝Lq＝5．45mH，定子电阻 R＝0．9411Ω，永磁体磁链 ψf＝0．1819Wb，转动惯量 J＝0．003kg·m2，摩擦系数 B＝0．008N·m·s。

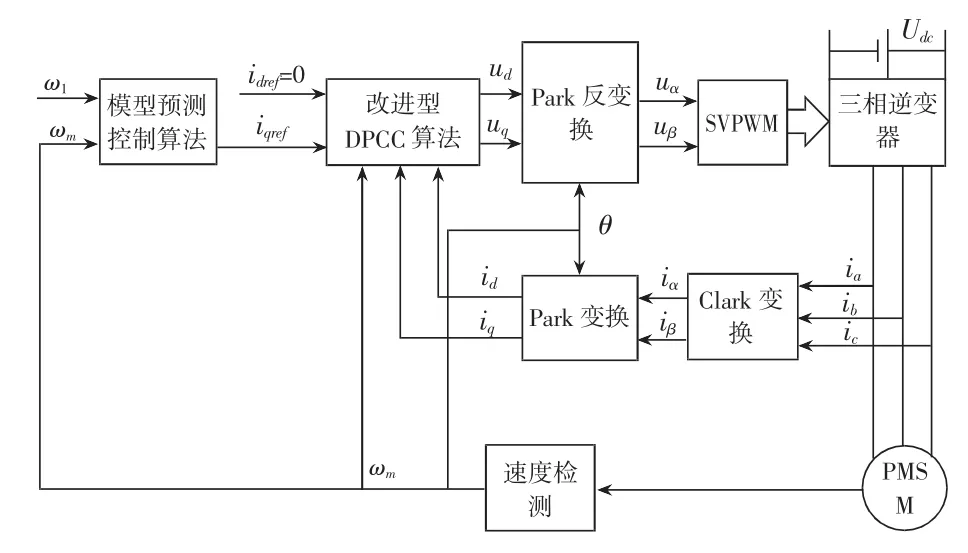
图1 PMSM电流预测控制系统结构框图

初始时，PMSM在给定转速600r／min下空载启动，在 0．3s时突加 2．39N·m 的负载，然后在 0．5s时将负载改变为 1．2N·m，仿真时间设置为 0．6s，分别将传统PI矢量控制、MPC＋改进DPCC策略进行转速对比仿真。

从图2电机转速对比的仿真波形可知，传统PI控制下PMSM启动超调大，动态响应时间最长，在突加、减负载时，回到给定转速调节时间长，转速落差变化较大。MPC＋改进DPCC方法动态响应快，能够稳定达到给定转速且实现无超调，在突加、减负载时，转速变化更小，调节时间更短，具有较好的抗负载干扰能力。

图2 电机转速对比的仿真波形

4 实验分析

PMSM控制实验平台如图3所示，该平台由A，B，C，D，E，F，G 七部份组成。其中A 为上位机，B为TMS320F28335实用板，C为功率板，D为15V开关电源，E为220V开关电源，F为永磁同步电机，G为磁粉制动器。

图3 PMSM控制实验平台

PMSM参数与仿真一致，在该平台上，分别对采用改进DPCC控制的系统与采用PI控制器的矢量控制系统进行实验，并将转速波形进行了对比。实验时两系统工况相同，给定转速为500r／min，某一时间突加相同负载，从图4传统PI控制转速波形和图5改进DPCC控制转速波形可以得到：改进DPCC控制器相对于PI控制器，突加负载时，电机转速变化小，电机转速稳定时间快，很快就能达到动态平衡。

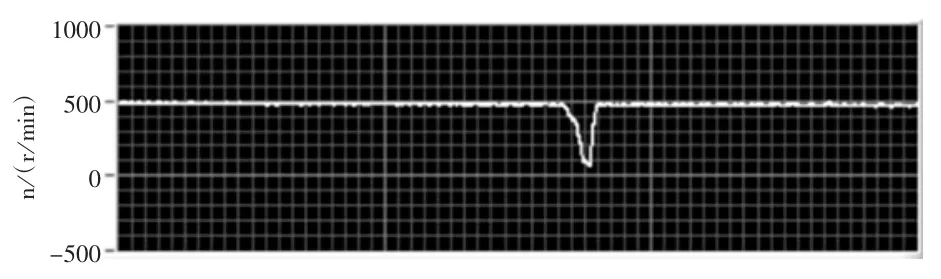
图4 传统PI控制转速波形

图5 改进DPCC控制转速波形

5 结论

为了解决传统PI矢量控制易出现超调、动态响应慢及抗负载干扰能力差等问题，本文在电流环提出带延时补偿的无差拍电流两步预测控制方法，可有效提高系统的动态响应能力及电流稳态精度，同时在速度环引入模型预测控制方法，其输出值作为电流环的电流参考值，很好地解决了传统PI控制抗负载干扰能力较差的问题，使控制器表现出更好的控制性能。仿真结果表明，所提方法具有较好的动态响应能力，提高了系统的抗负载干扰能力，并通过了实验验证，对研究高性能的焊接机器人具有一定的工程应用价值。