一种基于虚拟矢量的T型三电平并网逆变器改进型模型预测控制策略

陈 隆 周扬忠

一种基于虚拟矢量的T型三电平并网逆变器改进型模型预测控制策略

陈 隆 周扬忠

（福建省新能源发电与电能变换重点实验室（福州大学），福州 350116）

T型三电平并网逆变器直流侧电容中性点电压（NP-V）的漂移直接影响并网性能；逆变器并网系统参数的时变及未建模直接影响传统模型预测控制（MPC）精度。为此，本文通过构造不影响NP-V的虚拟中矢量、虚拟补充矢量参与MPC控制矢量集，以克服传统MPC在调制比较高时NP-V不平衡的缺点；建立电流跟踪单目标代价函数，无需整定权重因子；根据直流母线电容状态优选小矢量，进一步控制NP-V平衡；提出一种扩张状态观测器（ESO）观测逆变器并网系统未建模部分，并把观测结果补偿到并网参考电压上。实验结果表明，优化MPC策略消除了NP-V低频振荡，其逆变器输出电流总谐波畸变率（THD）低于传统MPC策略。

T型三电平并网逆变器；模型预测控制（MPC）；虚拟中矢量；扩张状态观测器（ESO）

0 引言

T型三电平逆变器具有电流通路器件数量少、导通损耗小、不需要钳位二极管等优点，被广泛应用于可再生能源系统和电机驱动[1-4]。尽管T型三电平逆变器具有很多优势，但是如果中性点电压（neutral-point voltage, NP-V）没有得到有效控制，将直接导致逆变器工作性能降低。

模型预测控制（model predictive control, MPC）与传统的线性控制方法不同，可以解耦相互依赖的控制回路，从而提高系统的动态响应。MPC在T型三电平并网逆变器的应用中，通常需要设计双目标代价函数，其中一项用于调节NP-V波动，另外一项用于实现电流跟踪[5-6]。由于代价函数中权重因子的值直接影响MPC对逆变器的控制性能，所以需要对权重因子进行精确调节，导致费时且困难。文献[7]提出离散空间向量与MPC结合的方案，该算法无需查找表即可计算出参考电压矢量，但是需要设计一个代价函数来平衡直流母线电容电压。此外，传统MPC策略是建立在精确被控对象数学模型的基础上，但在大多数情况下，被控对象的部分数学模型是未知的或不准确的，从而降低了MPC的控制效果[8]。文献[9-10]通过线性外推和基于雅克比迭代的电感在线辨识方案，提高预测模型的精度。

本文针对T型三电平逆变器提出一种基于虚拟矢量的改进型模型预测控制策略。该控制策略不仅可以简化代价函数设计，还可以提高并网逆变器系统性能。

1 T型三电平并网逆变器模型预测控制原理

1.1 T型三电平并网逆变器数学模型

图1为T型三电平并网逆变器系统的结构，该系统由直流电源dc供电，功率模块后端经LCL滤波器后并入电网。其中功率模块包含有母线电容1、2及12个功率开关管，定义功率开关管开关信号为

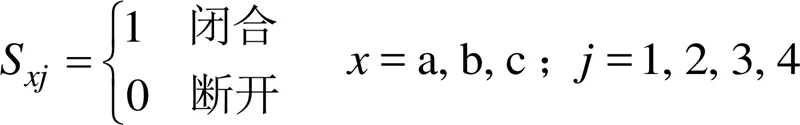
逆变器每一相通过不同的开关组合可以产生三种输出状态，即1、0、-1，用S表示；三相共计33=27种电压矢量，其幅值和空间位置如图2所示。假设直流侧电容中点电压平衡，即c1=c2；逆变器输出相电压为un（=a, b, c），开关状态与输出相电压关系见表1。

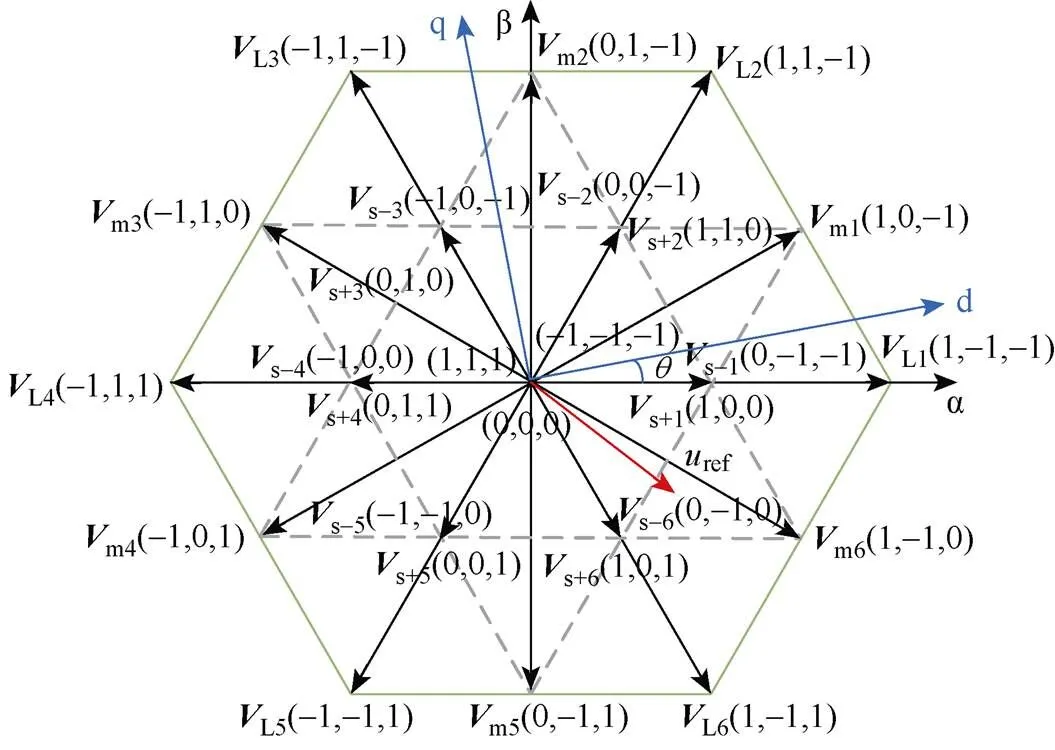
图2 T型三电平逆变器输出电压空间矢量图

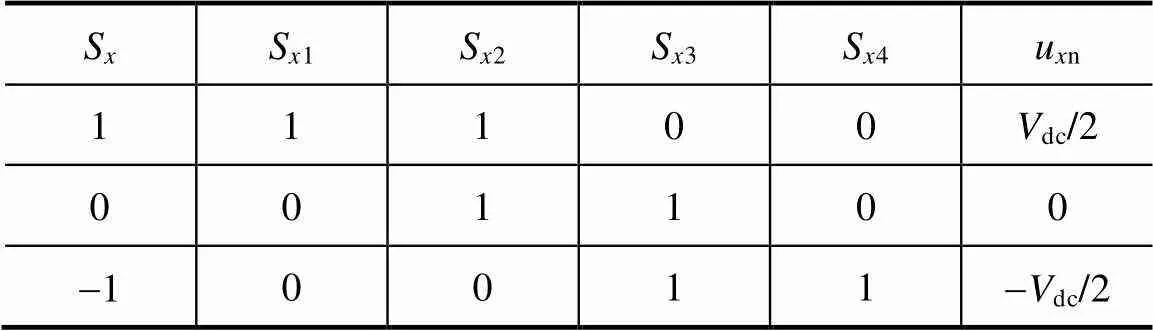
表1 开关状态与输出相电压关系

根据图1中的电流参考方向，在静止坐标系下建立逆变器的动态模型为

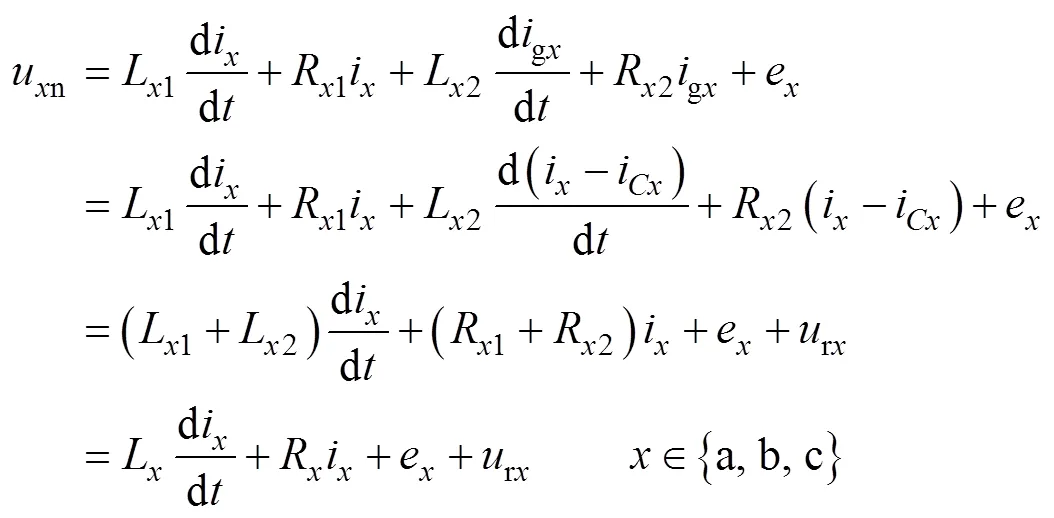
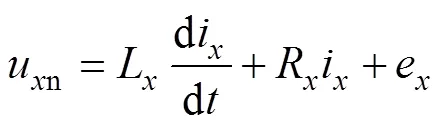
建立直流侧电容动态模型，有1=2，当直流源电压恒定时，电容电流表达式为

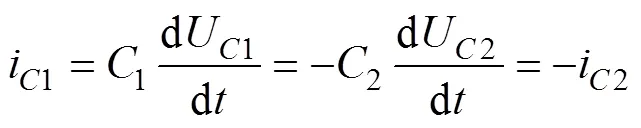
由图1结合表1可知，T型三电平并网逆变器的直流侧电容中点电流o为

（5）

将式（4）和式（5）合并得

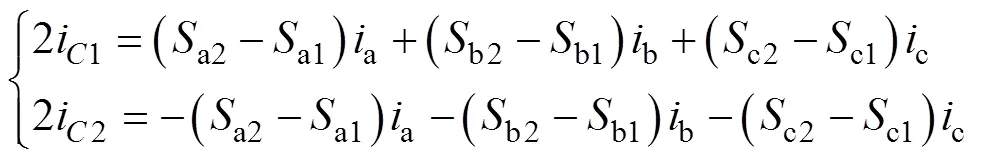
1.2 传统模型预测控制策略

传统的模型预测控制是将图2中的27种矢量依次代入逆变器离散数学模型中，通过代价函数进行评估选择最优的开关状态用于下一次迭代。因为采样周期s足够短，可以使用前向欧拉法，将式（3）和式（4）离散化后得到逆变器离散数学模型，即

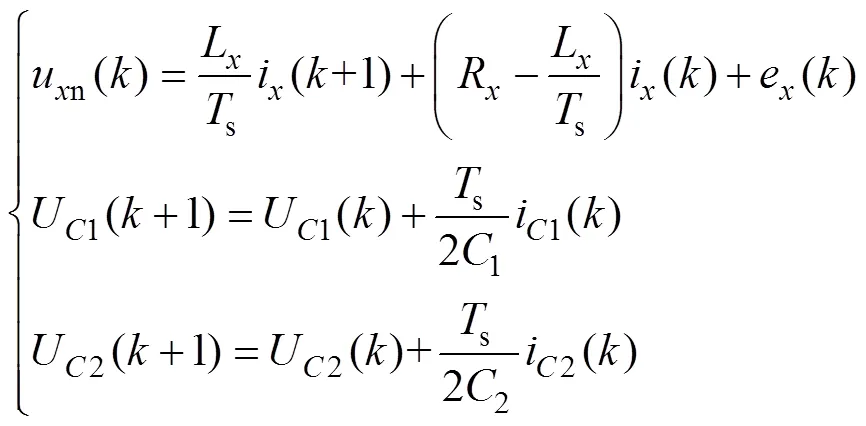
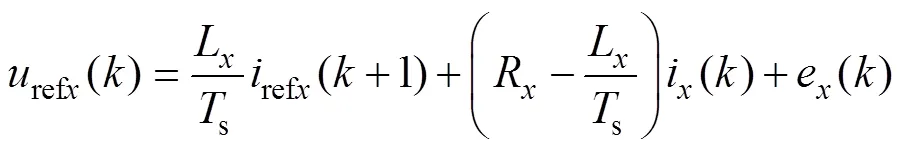
MPC无需复杂的坐标系变换，选择使设计代价函数最小的开关状态用于下一时刻控制迭代。本文在三相静止坐标系下，以电压为约束条件为例，建立代价函数为

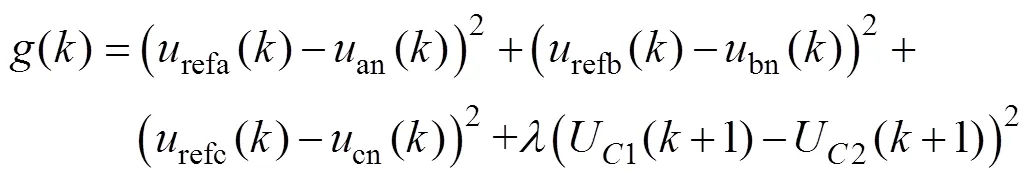
2 基于虚拟矢量的T型三电平并网逆变器模型预测控制方法

2.1 考虑中点电压平衡的电压矢量集构建

如果在一个控制周期内，直流侧电容中点电流o的平均值不为零，会造成上下电容充放电不平衡，引起中点电压振荡甚至漂移。假设系统三相无中线，则任何时刻满足a+b+c=0，根据式（5）可筛选出直流侧电容中点电流值o≠0的矢量是正小矢量、负小矢量和中矢量。若逆变器输出电流与输出电压保持同相，归纳这些矢量对母线电容电压状态的影响效果见表2。

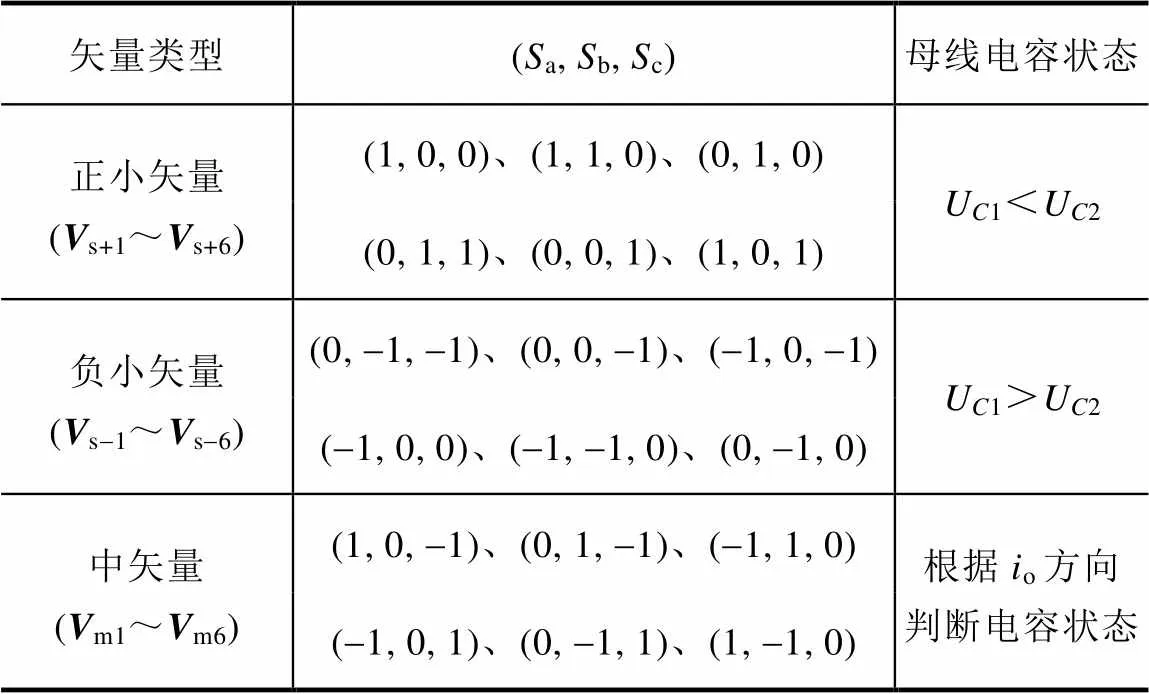
表2 中小矢量开关状态与母线电容状态

在调制系数较高和低负载功率因数的工况下，小矢量的作用时间比例小，动用小矢量不足以补偿中矢量带来的中点偏移量。为了克服这一问题，本文构造虚拟矢量进一步解决NP-V不平衡问题。

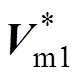
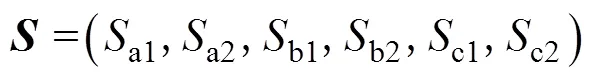
1）虚拟中矢量合成

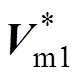
图3 包含虚拟矢量的T型三电平空间矢量图

2）虚拟补充矢量合成

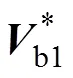
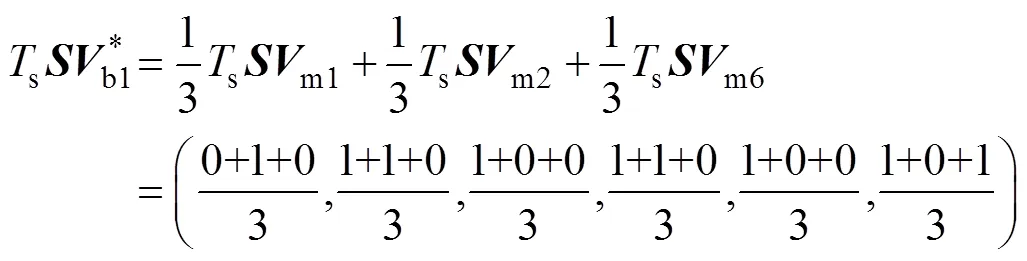
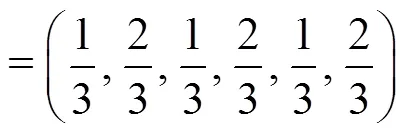
表3总结了虚拟中矢量和虚拟补充矢量的拓展状态。图3为所有参与本文MPC的电压矢量，共有33个空间矢量。将正负小矢量代入式（3）并结合表2可知，对应的正负小矢量产生的相电压是相同的，但对母线电容作用效果是相反的。因此，本文只需要27次寻优，即分别把零矢量、正小矢量、虚拟补充矢量、虚拟中矢量和长矢量代入式（8）中；再根据时刻母线电容状态，选用合适小矢量。从而实现单代价函数下的T型三电平逆变器控制，其代价函数更新为

表3 虚拟矢量与其拓展状态

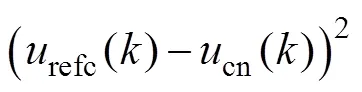
2.2 模型误差补偿策略

1）考虑模型误差的逆变器动态运动模型

上述MPC采用模型本质是忽略式（2）中模型扰动项rx，从而产生控制误差；另外模型中电感等参数经常与实际对象存在偏差，导致MPC性能降低。如何补偿上述模型误差对提高MPC性能非常 重要。

可以看出，逆变器电流环路为一阶非线性系统。令参数不匹配产生的电压误差为内部未知扰动f(i)(-rxDLdi/dDRi)，网侧电压为外部已知扰动w()-e控制增益b=1/L，则

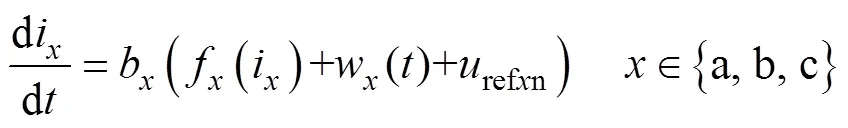
以网侧参考电压为系统输入us，i为系统输出y，i为状态变量x1，构建一阶系统为

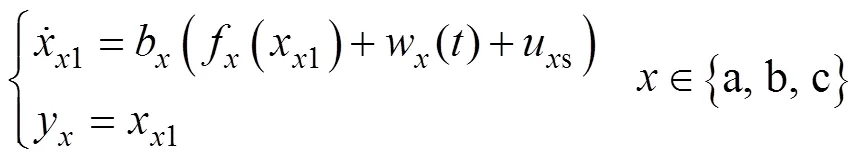
令广义扰动x2=a(x1)=bf(i)+bw()，构建新系统为

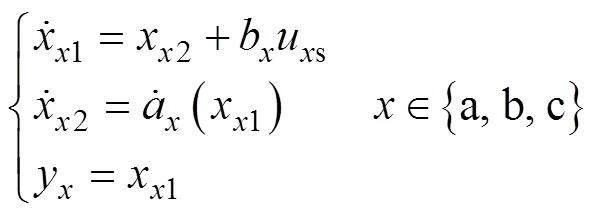
2）建立逆变器中的扩张状态观测器

扩张状态观测器（extended state observer, ESO）能够根据系统输入量refxn与输出量i对状态变量x1、x2进行估计，进而实现动态扰动前馈补偿，针对式（17）建立ESO为

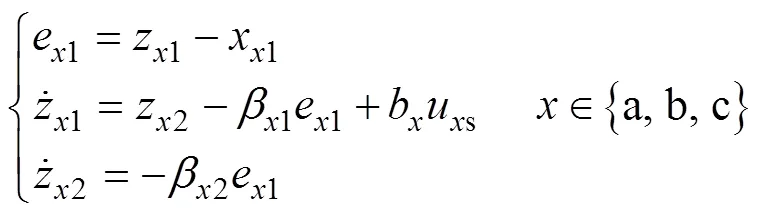
式中：z1、z2分别为x1和x2的估计；1、2决定了ESO误差跟踪状态，当且仅当2＞0时，误差是逐渐稳定的。针对上述ESO，写出其特征多项式为

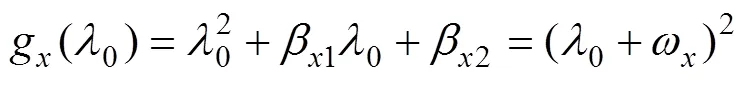
定义特征向量值为ESO的带宽，则有

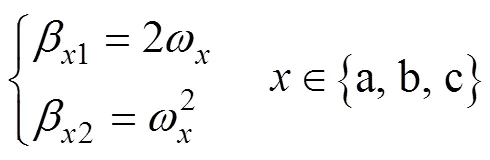
可以确定ESO的可调系数1、2，并简化参数整定。带宽越大，ESO的极点离虚轴距离越远，对误差的跟踪速率也就越快。然而带宽过大，ESO对采样噪声越敏感，导致观测器出现振荡。

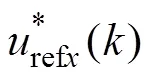
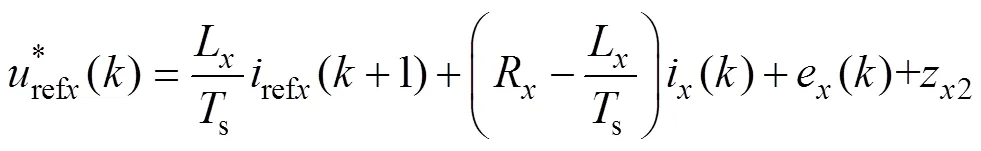
得到ESO补偿后的更新代价函数为

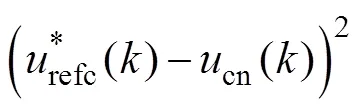
2.3 优化模型预测控制策略控制框图

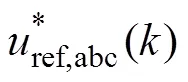
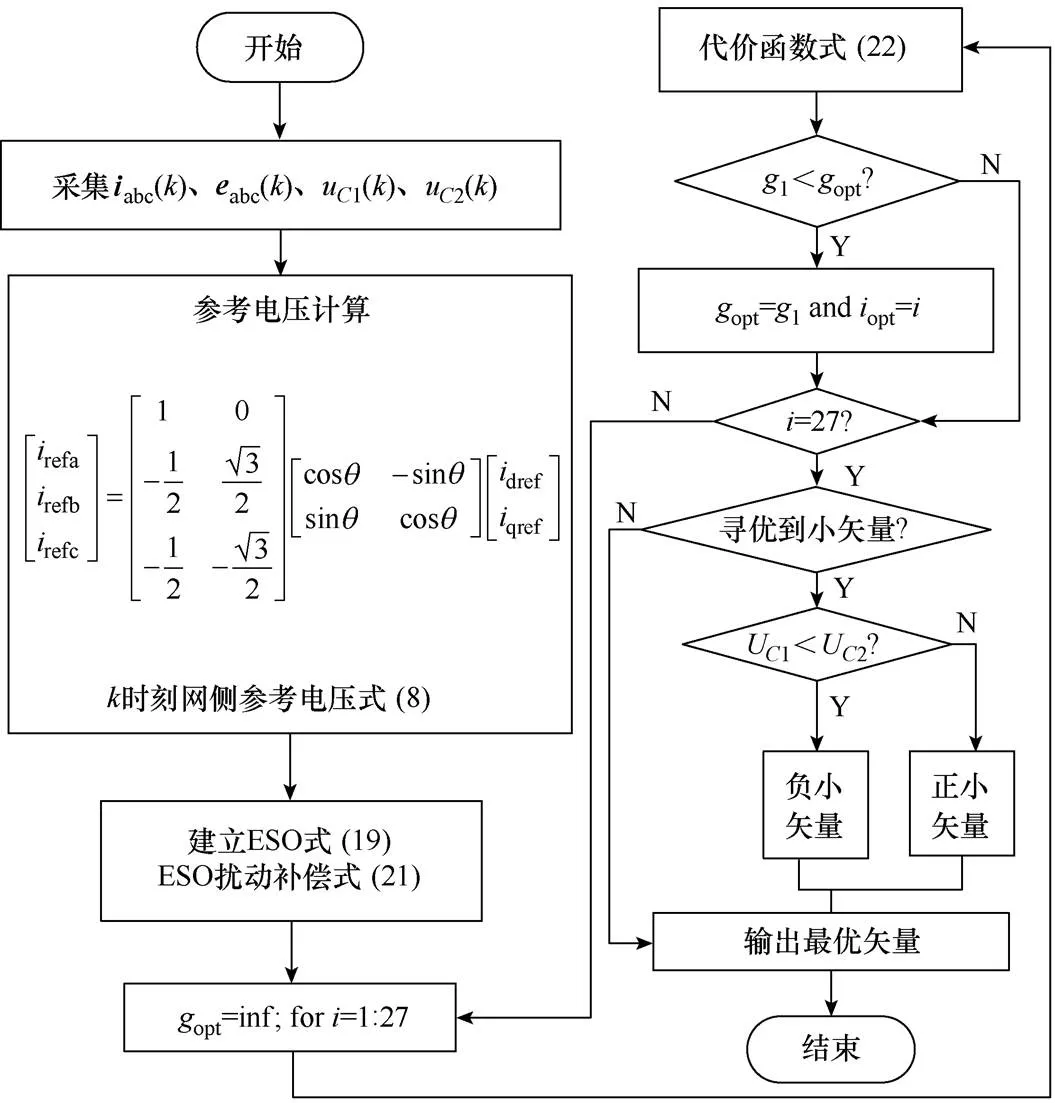
图4 改进型模型预测控制策略控制框图

3 实验

3.1 实验样机

结合上述理论分析，搭建T型三电平逆变器实验平台如图5所示，对所提控制策略进行实验验证。图5中共有三个功率模块，构成三相输出，每个功率模块由4个IKW15T120IGBT功率单管组成。电压电流采样信号由霍尔CC6920和精密型电压互感器zmpt107—1接入调理电路实时采集，采集模拟信号进入主控芯片TMS320F28377D进行运算后，输出功率管驱动信号，进而对功率模块进行控制。实验中逆变器系统参数见表4。

3.2 稳态对比实验

分析比较不同控制策略的逆变器稳态下的输出性能、NP-V的控制能力。分别对传统MPC、优化MPC进行实验分析。给定的三相参考电流峰值为8A。实验结果如图6所示。从图6（a）和图6（b）可见，优化MPC逆变器输出电流总谐波畸变率（total harmonic distortion, THD）更低；从图6（c）可见，优化MPC的NP-V波动小，NP-V电位差仅在±0.4V波动。

图5 T型三电平逆变器实验平台

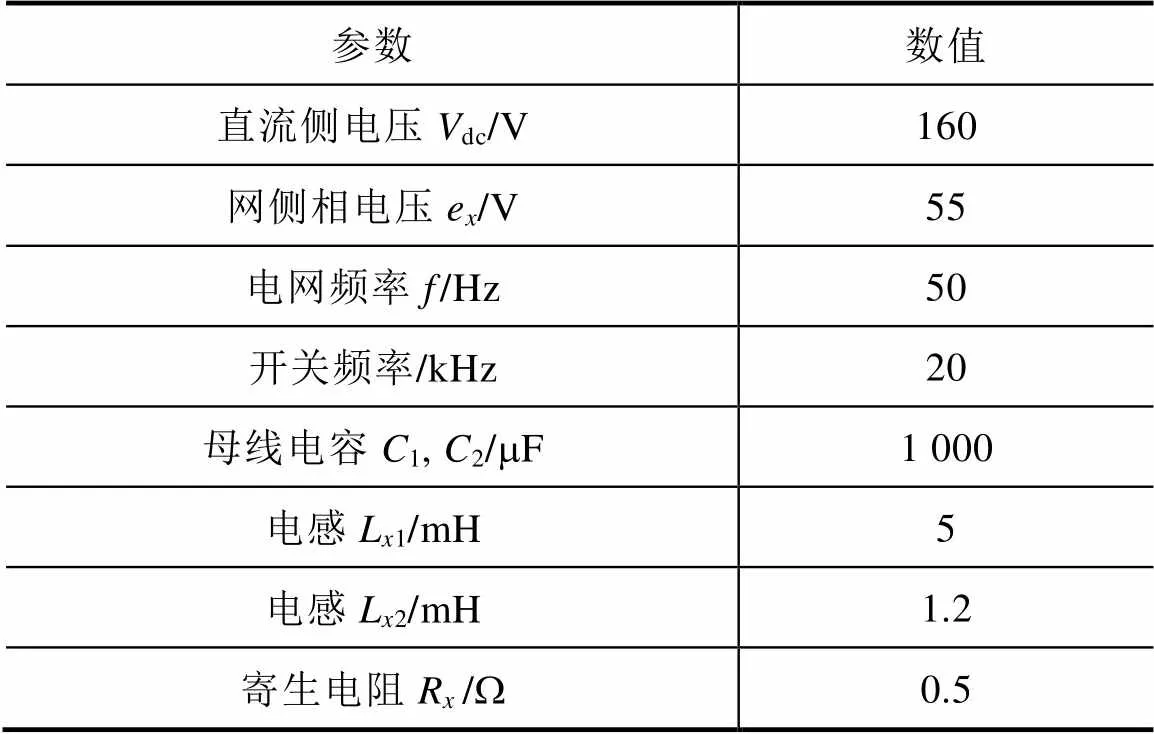
表4 系统参数

图6 不同控制策略的逆变器性能比较实验结果

3.3 动态实验

图7为不同策略下的电流阶跃实验结果。指令电流幅值由4A跃升到8A时，实际电流能在1ms内到达指令值并保证系统稳定性，证明了优化MPC依然保留着传统MPC优秀的动态响应性能。

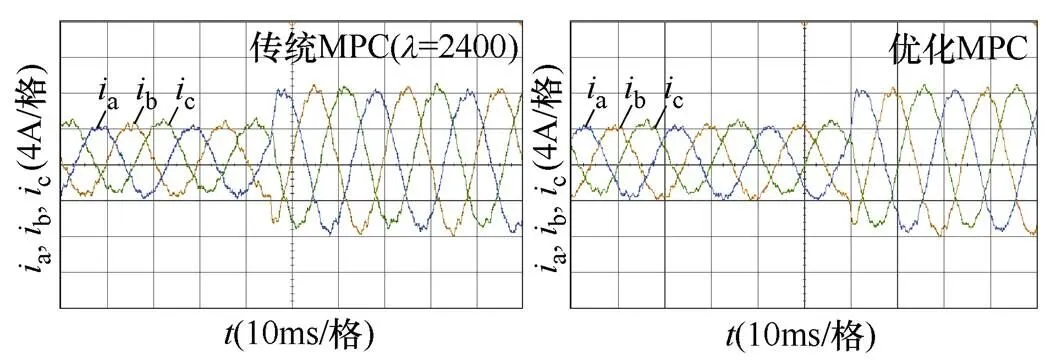
图7 不同控制策略的逆变器输出电流阶跃实验结果

3.4 电感失配下的ESO补偿实验

分别在基于虚拟矢量单代价函数无ESO补偿的MPC策略和优化MPC策略下进行电感不适配实验。其中，电感静态值为6.2mH，分别设置模型电感值为7.5mH、6.2mH、5mH。不同控制策略的电感失配的电网电流THD如图8所示，由图8可知，因模型电感值不匹配，提高了电网电流谐波分量；通过ESO观测补偿，有效解决了MPC因控制模型精度而造成的控制误差。

图8 不同控制策略的电感失配的电网电流THD

4 结论

本文以T型三电平并网逆变器为研究对象，提出了一种基于虚拟矢量的优化模型预测控制策略。通过稳态实验和动态实验验证了基于虚拟矢量的MPC策略在并网性能和平衡直流侧中性点电压能力方面的提高，并通过电感失配实验证明了ESO补偿策略的有效性。

[1] 张建忠, 胡路才, 徐帅. 一种零序电压注入的T型三电平逆变器中点电位平衡控制方法[J]. 电工技术学报, 2020, 35(4): 807-816.

[2] 李倩倩, 夏蓉花, 刘战, 等. 有源中点钳位型三电平并网逆变器多目标优化预测控制[J]. 电气技术, 2021, 22(7): 13-18.

[3] WANG Xueqing, WANG Zheng, YAN Chunxing, et al. Fault-tolerant control of common electrical faults in dual three-phase PMSM drives fed by T-type three- level inverters[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 481-491.

[4] XU Shuai, SUN Zhenyao, YAO Chunxing, et al. Model predictive control with constant switching frequency for three-level T-type inverter-fed PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 8839-8850.

[5] XIA Zhenglong, LIU Zhan, GUERRERO J M. Multi- objective optimal model predictive control for three- level ANPC grid-connected inverter[J]. IEEE Access, 2020, 8: 59590-59598.

[6] 杨勇, 谢门喜, 樊明迪. T型三电平单相逆变器有限开关状态模型预测控制方法[J]. 电机与控制学报, 2019, 23(3): 120-126.

[7] YANG Yong, WEN Huiqing, FAN Mingdi, et al. Fast finite switching state model predictive control method without weighting factors for T-type three-level three- phase inverters[J]. IEEE Transactions on Industrial Informatics, 2019, 15(3): 1298-1310.

[8] 辛业春, 王延旭, 李国庆, 等. T型三电平并网逆变器有限集模型预测控制快速寻优方法[J]. 电工技术学报, 2021, 36(8): 1681-1692.

[9] 唐圣学, 邢路铭, 黎霞, 等. 逆变器有限集模型预测控制参数不匹配补偿方法研究[J]. 电机与控制学报, 2021, 25(11): 46-55.

[10] 李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15): 3450-3460.

An improved model predictive control based on virtual space vector for T-type three-level grid-connected inverters

CHEN Long ZHOU Yangzhong

(Fujian Key Laboratory of New Energy Generation and Power Conversion (Fuzhou University), Fuzhou 350116)

The drift of the neutral-point voltage (NP-V) at the DC-side capacitor of the T-type three-level grid-connected inverter directly affects the grid-connected performance. The model predictive control (MPC) accuracy is directly affected by the time variation and non-modeling of grid-connected inverter system parameters. In order to overcome the defect of NP-V imbalance in traditional MPC when the modulation is relatively high, a virtual neutral vector and a virtual compensation vector are constructed to participate in the control vector set of MPC without affecting NP-V in this paper. The single objective cost function of current tracking is established, and the small vector is optimized according to the DC bus capacitance state without setting the weight factor to further control the NP-V balance. An extended state observer (ESO) is proposed to observe the non-modeling part of the grid-connected inverter system and add the observation results to the grid-connected reference voltage. The experimental results show that the optimal MPC strategy eliminates NP-V low-frequency oscillations, and its total harmonic distortion (THD) is lower than that of the traditional MPC strategy.

T-type three-level grid-connected inverters; model predictive control (MPC); virtual middle space vector; extended state observer (ESO)

2022-06-08

2022-06-27

陈 隆（1996—），男，福建省福州市人，硕士研究生，主要从事新能源发电系统的研究工作。