基于完备局部均值分解和相关分析的光伏发电侧电-氢混合储能优化配置

刘语忱 闫群民 郭 阳 刘新宇 桑兴勇

基于完备局部均值分解和相关分析的光伏发电侧电-氢混合储能优化配置

刘语忱 闫群民 郭 阳 刘新宇 桑兴勇

（陕西理工大学电气工程学院，陕西 汉中 723001）

光伏出力的间歇性和波动性对电网的冲击仍然较大，利用储能装置对电能进行时空平移能够提高光伏发电的可控性、提高供电质量。本文提出由蓄电池、超级电容、氢能组成的混合储能系统（HESS）的容量配置方法。首先建立光伏电站和储能系统的数学模型，将电站调度功率与光伏实际输出功率的差值作为HESS参考功率，利用完备局部均值分解（ELMD）和皮尔逊积矩相关系数（PPMCC）确定HESS参考功率的高频、中频和低频分量，在三种储能装置的荷电状态（SOC）约束下，依次对超级电容、氢储能、蓄电池功率进行分配，同时考虑蓄电池循环寿命，并将蓄电池损伤模型纳入HESS全寿命周期投资成本（LCC）评估体系中。最后，通过某光伏电站实际调度数据在Matlab中进行仿真，证明了本文方法可有效将HESS功率按不同工作频段分解并重构，体现了HESS相对于单一储能在经济与技术上的优越性。

光伏发电；混合储能；完备局部均值分解（ELMD）；相关系数；容量配置

0 引言

为实现传统化石能源结构向新能源结构的过渡，发展风电、光伏发电是必然要求[1]。随着新能源在电网中渗透率的逐年增加，如何提高新能源发电的可控性成为近些年研究的热点问题[2]。

储能系统具有易控制、能量可双向流动的特性，是提高新能源发电利用率的有效解决方案[3-4]。按照储能元件功率密度及能量密度的大小，可将储能装置划分为功率型储能和能量型储能。然而，目前单一介质的储能装置无法同时满足快速响应、大规模存储的需求，因此部分学者对储能装置取长补短，将功率型和能量型储能装置组合配置在新能源发电侧，以满足高功率、大容量的需求[5]。

现有研究多以两种介质的储能装置组成混合储能系统（hybrid energy storage system, HESS），配置在新能源并网出口或电网侧，对发电侧多元储能的协同控制与配置方法的研究较少。文献[6]采用经验模态分解（empirical mode decomposition, EMD）将HESS功率划分为振动频率由高到低的不同分量，高频分量由超级电容吸收，低频分量由蓄电池吸收，之后考虑储能寿命周期投资成本，在风力发电侧对HESS进行配置。文献[7]根据风电出力频谱特性，提出了储能双层容量规划模型，利用EMD对风力发电侧液流电池-压缩空气储能进行优化配置。文献[8]通过对风电原始出力进行自适应噪声完备经验模态分解（complete ensemble empirical mode decom- position with adaptive noise, CEEMDAN），将风电功率分为高频与低频分量，采用能量熵对HESS容量进行配置。文献[9]考虑风电平滑度指标，基于变分模态分解（variational mode decomposition, VMD）分解HESS参考功率，最后采用遗传算法取得HESS最优配置容量。

还有少量文献对三种及以上储能装置耦合的HESS的配置方法进行了研究。文献[10]采用燃料电池、锂电池和超级电容组合的HESS，通过非线性模糊逻辑控制策略规划储能装置的容量，但该方法对功率分配不够精确，并且没有考虑储能装置的循环寿命。文献[11]结合压缩空气储能、锂电池和超级电容器三种储能装置的优点，使用二次平均滤波法分配储能功率，但压缩空气储能结构复杂，属于能量型储能装置，充放电时长多为小时级，不适宜配置在新能源发电侧。

氢能作为低碳、易制备的储能介质，配置在新能源发电侧可达到节能减排的要求[12]。因此，本文发挥不同储能装置高功率、高密度、清洁的特性，提出一种由超级电容、氢储能、蓄电池组成的HESS的容量配置方法。采用完备局部均值分解（ensemble local mean decomposition, ELMD）将HESS参考功率“打散”，按照高频至低频模态排列，之后通过皮尔逊积矩相关系数（Pearson product-moment correla- tion coefficient, PPMCC）对相邻两模态分量做相关性分析，并令“打散”后的模态分量按高、中、低频重构，超级电容承担高频分量、氢储能承担中频分量、蓄电池承担低频分量，同时预测蓄电池使用寿命，最后对得到的三种储能容量做全寿命周期成本（life cycle cost, LCC）评估，利用实际光伏采样数据进行仿真，证明本文HESS配置方法的有效性与可行性。

1 光储系统模型构建

1.1 光伏发电模型

影响光伏出力的因素主要有地理位置和当地天气。光照强度大致服从Beta分布（简称B分布），其概率密度函数为[13]

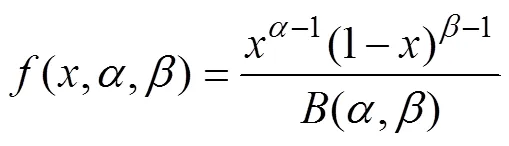
式中：为随机变量；为分布参数；(,)为B分布函数，其表达式为

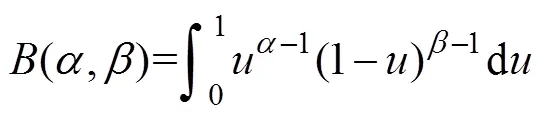
光伏各时刻输出功率与光照强度的关系为

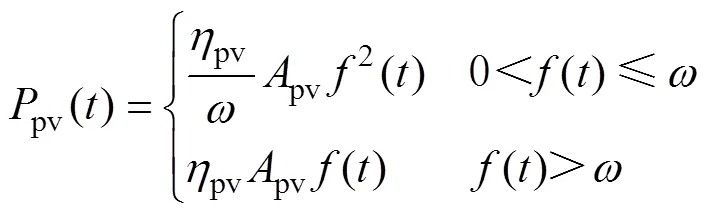
1.2 蓄电池模型

荷电状态（state of charge, SOC）是用来描述蓄电池工作状态的变量，其数值可用剩余容量与额定容量的比值表示[14]。SOC=1表示蓄电池电量已充满；SOC=0表示蓄电池电量已放完。本文三种储能装置SOC初始值均设为SOC0=0.5。SOC的动态计算表达式为

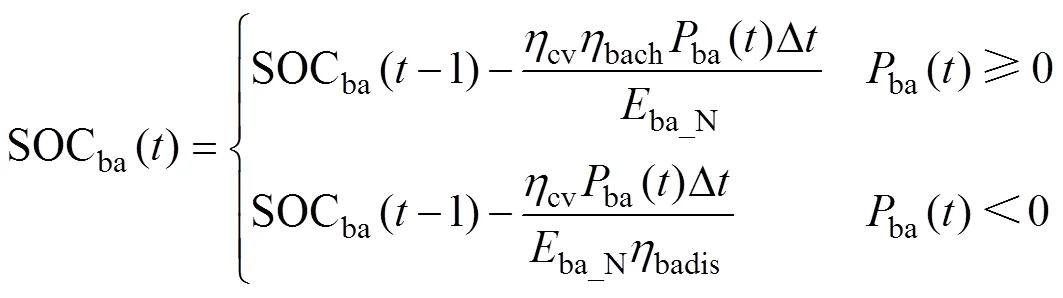
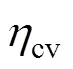
1.3 超级电容模型

超级电容的充放电过程也可用荷电状态表达，其数学模型为

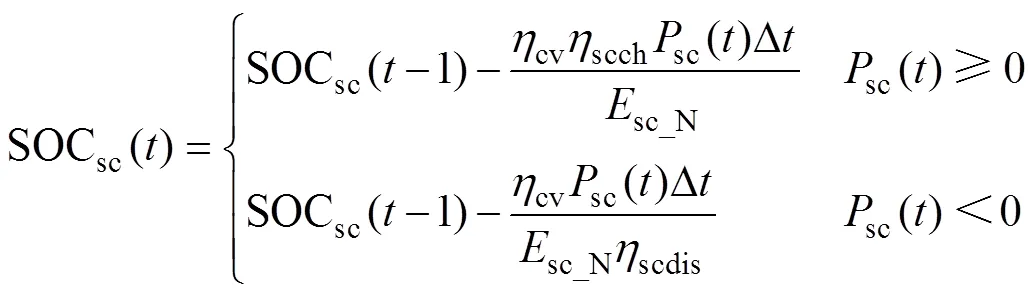
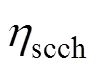
1.4 氢储能模型

本文主要考虑氢储能系统的供电过程，供热过程不做分析，且对氢储能系统的工作状态统一用功率和能量描述。构成氢储能系统的模型如下。

1）电解槽模型

电解水制氢常用的电解槽主要为质子交换膜（proton exchange membrane, PEM）电解槽，将水电解产生氢气和氧气[15]。电解槽制氢消耗的功率为

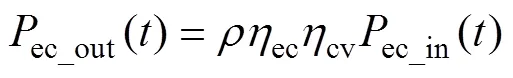
式中：ec_in()为电解槽从交流母线获得的有功功率；为每消耗1kW有功功率产生的氢气量，其值为25.2g；为电解槽产氢效率，本文设为70%。

电解槽制氢过程可理解为氢储能系统运行在充电状态，其电量的定义方式可同蓄电池和超级电容的SOC，定义式为

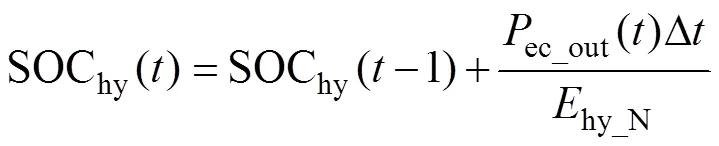
式中：SOChy()为氢储能系统实时荷电状态；hy_N为氢储能系统额定容量。

2）燃料电池模型

燃料电池从储氢罐中获取氢气，将氢气作为燃料把化学能转换为电能，通过逆变器将功率传输至交流母线[16]。燃料电池传输至交流母线的功率为

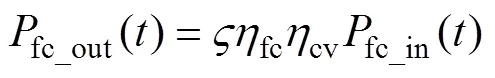
燃料电池耗氢过程可理解为氢储能系统运行在放电状态，其电量的定义式为

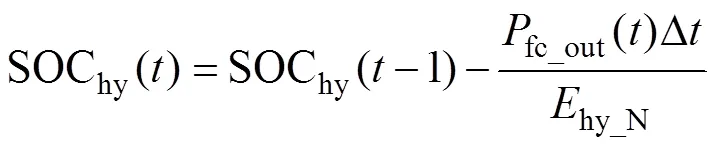
3）储氢罐模型

直流电通过电解槽时，电解槽内发生氧化还原反应产生氢气和氧气，之后将氢气存储至储氢罐中。下面对储氢罐进行数学建模。储氢罐存储、释放氢气时的表达式[17]分别为

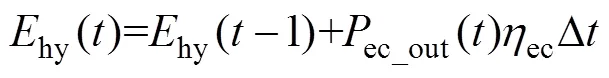
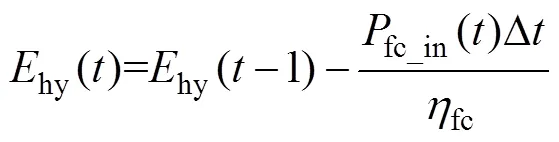
式中，hy()为时刻储氢罐的能量（kWžh）。

综上，本文建立的光储系统模型由光伏电站、氢储能系统、蓄电池、超级电容组成，其拓扑结构如图1所示。

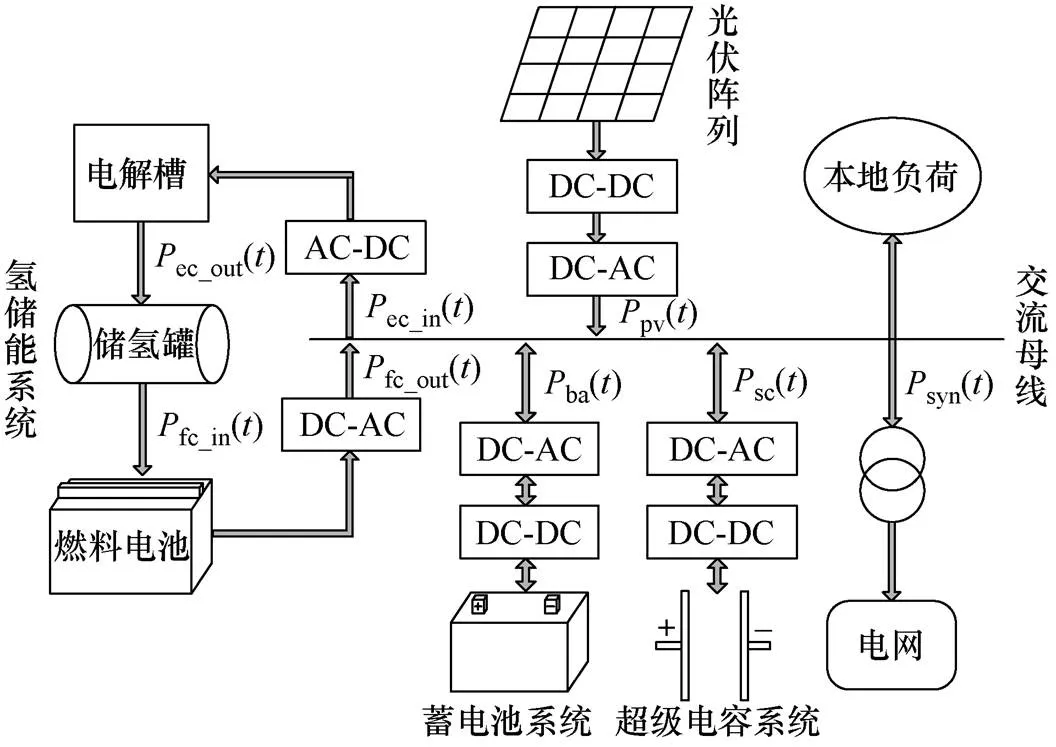
图1 光储系统拓扑结构

根据交流母线上的功率流向，可得

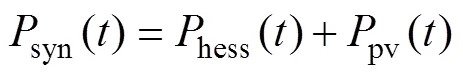
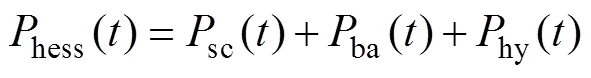
式中：syn()为电网调度功率（光伏并网功率）；hess()为混合储能系统参考功率；pv()为光伏实际输出功率；hy()为氢储能系统充放电功率，放电时hy()=fc_out()，充电时hy()=ec_in()。

2 HESS功率分配方法

2.1 基于ELMD的HESS功率分解

局部均值分解（local mean decomposition, LMD）可根据信号本身的变化规律将一组非平稳、非线性信号通过循环迭代的方式分解为若干乘积函数（product function, PF）和一个残余分量之和[18]。但LMD存在端点效应，且分解结果会出现模态混叠。ELMD则是在原始信号中多次添加白噪声信号，利用白噪声信号频率均匀分布的特性有效改变了原始信号极值点的分布，从而消除模态混叠，减小信号重构误差[19]。ELMD的分解步骤如下。

ELMD算法流程如图2所示，此处hess()为待分解的HESS参考功率。hess()分解步骤如下：

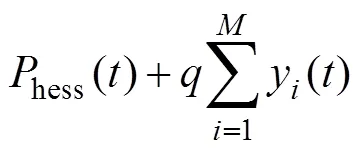
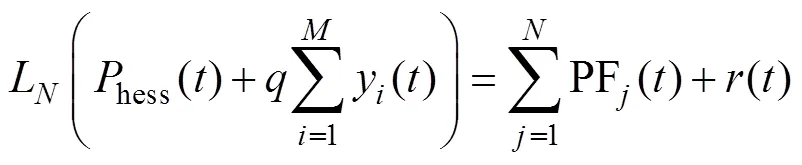
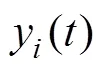
2）对LMD得到的阶PF分量累加并求平均值，得到ELMD分解出的第一阶PF分量，即

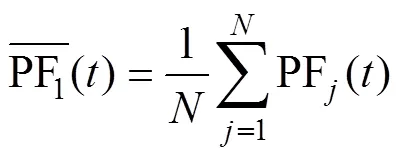
3）将原始信号与ELMD分解出的第一阶PF分量做差，得到第一阶余量为

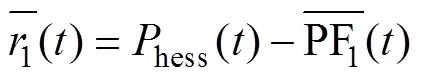
4）重复步骤1）～3），若余量为单调函数，则无法继续提取PF，算法终止。此时获得的PF分量共有个，那么原始信号hess()分解结果为

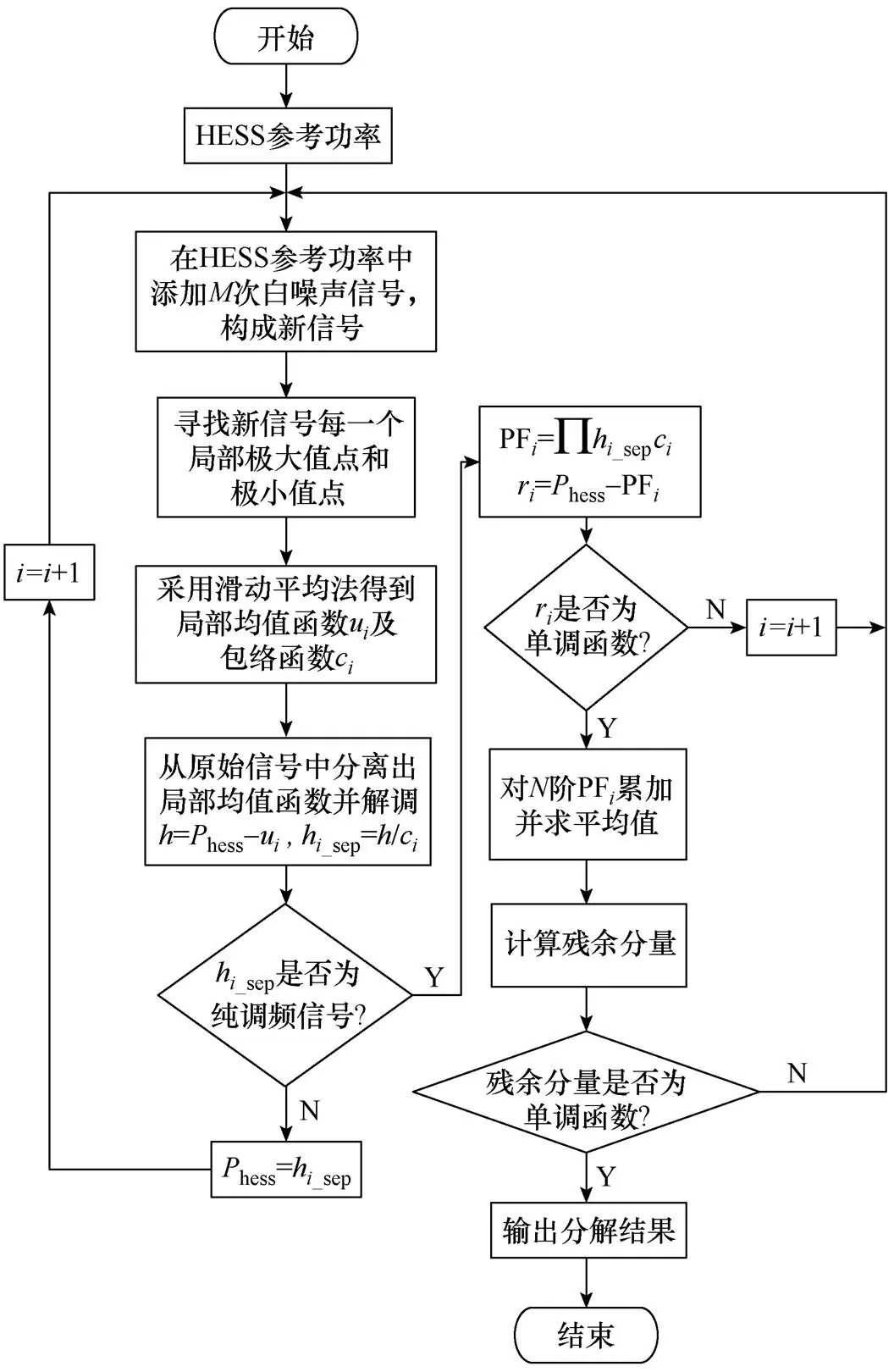
图2 ELMD算法流程

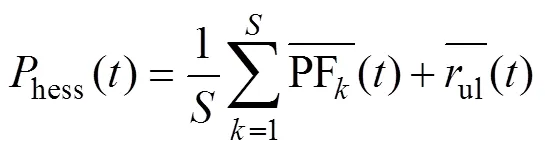
2.2 基于PPMCC的HESS功率分配

皮尔逊积矩相关系数可用来表征数据组和的线性关系及相关方向，并对结果作量化处理，本文用来分析信号间的耦合程度，计算式为

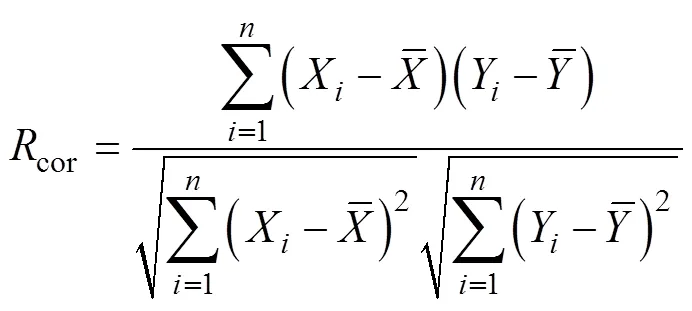
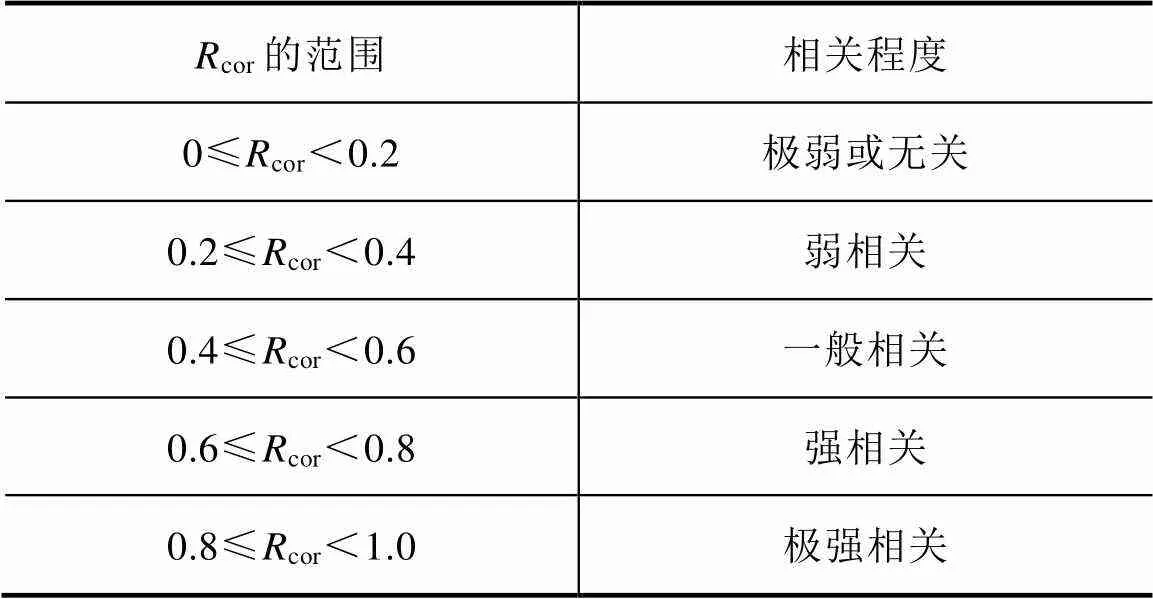
表1 皮尔逊积矩相关系数的评价标准

对PF分量作相关性分析的流程如图3所示。

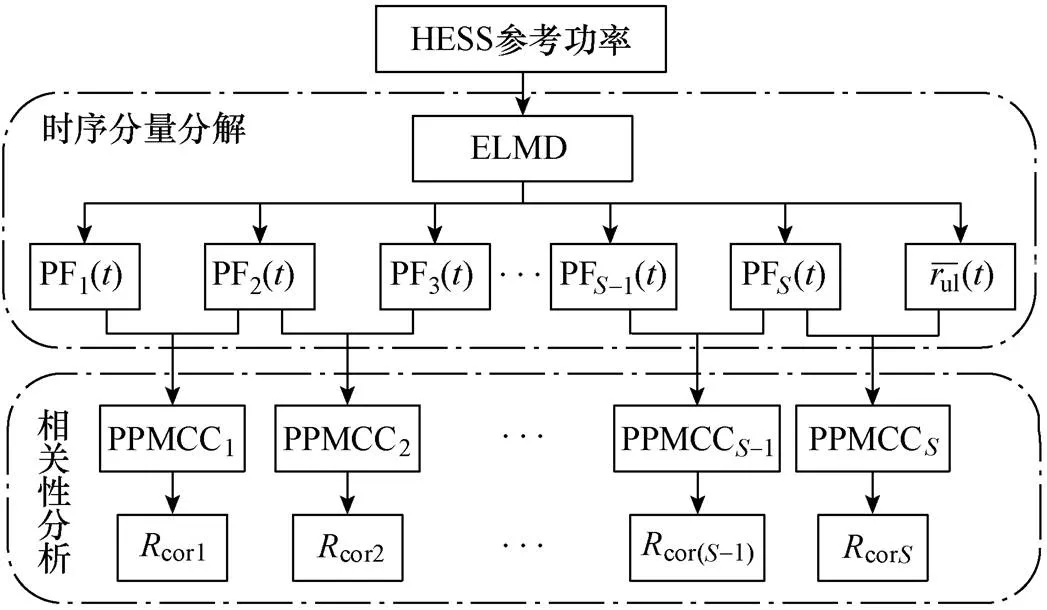
图3 ELMD-PPMCC分析流程

超级电容作为功率型储能装置，具有快速充放电能力（秒级）；氢储能、蓄电池作为能量型储能装置，具有大规模电能存储能力（兆瓦级），但充放电速度较慢（分钟至小时级）。因此这三种介质的储能装置应工作在不同频段，即超级电容工作在高频区间，氢储能、蓄电池工作在低频区间，然而蓄电池的循环寿命会受充放电频率的影响，充放电频率越高，其循环寿命下降越快，故本文在进行功率分配时，选择让蓄电池工作频段低于氢储能。结合上述分析，本文将HESS工作频段划分为高、中、低三段，高频段由超级电容承担，中频段由氢储能承担，低频段由蓄电池承担。

HESS参考功率通过ELMD-PPMCC的分析后，得到频率范围由高到低的个PF分量及相邻两个PF分量的相关系数，挑出相关程度最小的两个PF分量PF和PF+1（相关系数为R），重构PF+1与频率低于PF+1的分量，由蓄电池吸收；之后，挑出相关系数大小仅次于R的两个PF分量PF和PF+1（相关系数为R），重构PF与频率高于PF的分量，由超级电容吸收，再将PF+1与频率低于PF+1的分量进行叠加，由氢储能系统吸收。则HESS功率最终分配结果为

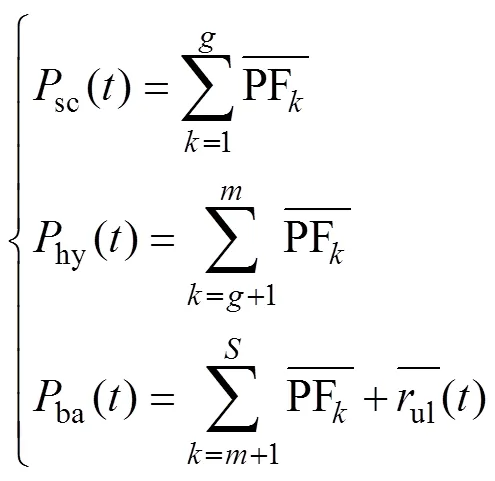
3 HESS优化配置方法

3.1 HESS配置的约束条件

储能系统在工作过程中，需要实时监测其充放电状态。储能装置满充或满放会加速储能本体的老化速度，循环寿命快速减少，故有必要对其荷电状态加以限制[21-22]。荷电状态约束条件为

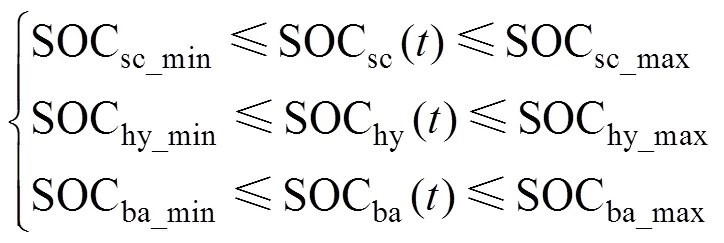
式中：SOCsc_max、SOCsc_min为超级电容荷电状态上、下限；SOChy_max、SOChy_min为氢储能系统荷电状态上、下限；SOCba_max、SOCba_min为蓄电池荷电状态上、下限。

3.2 HESS功率配置

为了提高光伏发电的利用率、减小并网点功率波动，储能系统应满足采样时间段内任意时刻的调度需求，因此超级电容、蓄电池、氢储能系统的额定功率应选择采样点内充放电功率中的最大值。分配公式如式（21）所示，由于分配方法相同，为表示方便，三种储能装置的额定功率统一表示为

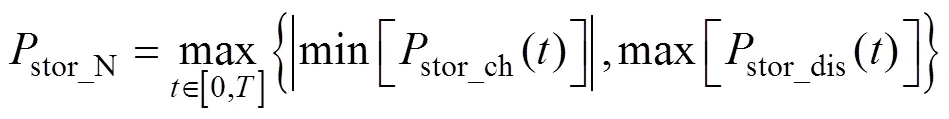
式中：stor_ch()为储能装置充电功率；stor_dis()为储能装置放电功率；为总采样点数。

4 循环寿命与经济性评估

4.1 寿命评估模型

超级电容在充放电过程中无化学反应，充放电过程可逆，故其循环寿命长。因此，本文将超级电容器寿命设为常数；氢储能系统的设计寿命一般是固定的，本文设定电解槽、储氢罐、燃料电池循环寿命分别为10年、15年、5年。但对于电化学储能装置蓄电池，温度、放电倍率和放电深度（depth of discharge, DOD）等内外因素都影响着其循环寿命和充放电效率。因深度放电会对蓄电池产生永久性损伤，故本文着重考虑DOD对蓄电池循环寿命的影响。

蓄电池循环寿命会随着DOD的增大而减小，蓄电池累计损伤模型为[23]

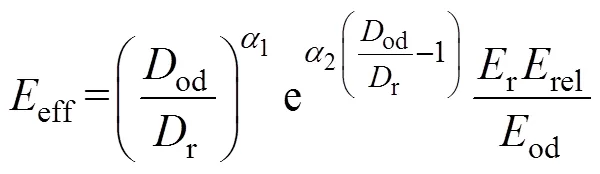
式中：od为蓄电池实际放电深度；eff、rel分别为有效放电容量和实际放电容量；r为额定放电深度；1、2为拟合系数；r、od分别为额定放电容量和等效放电容量。

若蓄电池在工作周期内共放电次，那么蓄电池实际寿命（年）为

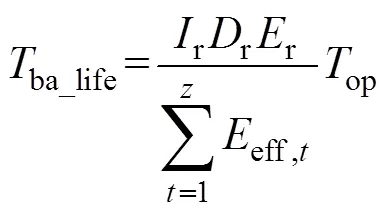
式中：r为蓄电池额定循环次数；op为蓄电池的工作周期。

4.2 投资成本分析

储能系统配置成本可作为电网运行经济性的一项评价指标，本文采用全寿命周期成本对储能配置结果作经济性评估，配置成本函数为[24]

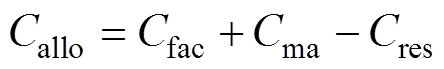
式中：fac为储能设备购置成本；ma为储能设备维护成本；res为储能设备回收残值成本。

1）储能设备购置成本

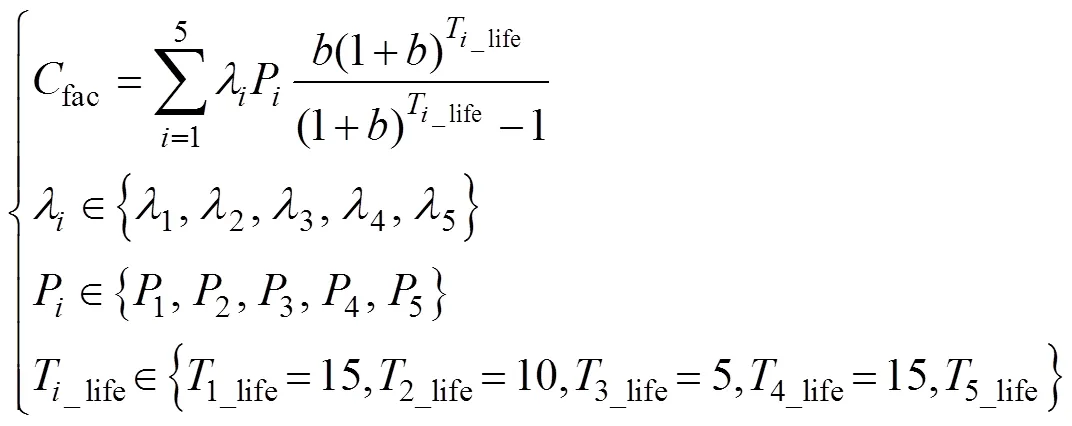
式中：1、2、3、4、5分别为超级电容、电解槽、燃料电池、储氢罐和蓄电池的单位容量购置成本；1、2、3、4、5分别为本文方法配置得到的超级电容、电解槽、燃料电池、储氢罐和蓄电池的额定容量；1_life、2_life、3_life、4_life、5_life分别为超级电容、电解槽、燃料电池、储氢罐和蓄电池寿命；为贴现率。

2）储能设备维护成本

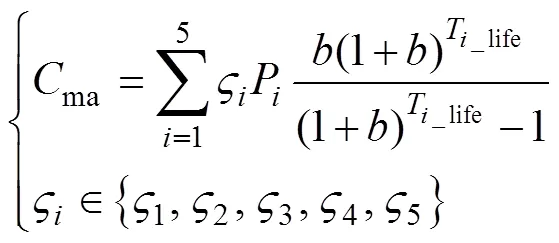
式中：1、2、3、4、5分别为超级电容、电解槽、燃料电池、储氢罐和蓄电池的单位容量维护成本。

3）储能设备回收残值成本

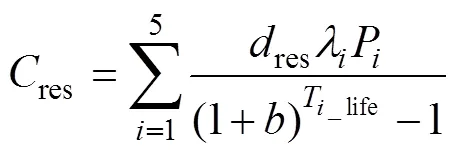
式中，res为回收残值率。

5 算例分析

以我国西北地区某100MW光伏电站半年内实际调度数据为研究对象，将数据导入Matlab 2018b中进行处理。光伏实际输出功率和电网调度功率如图4所示。

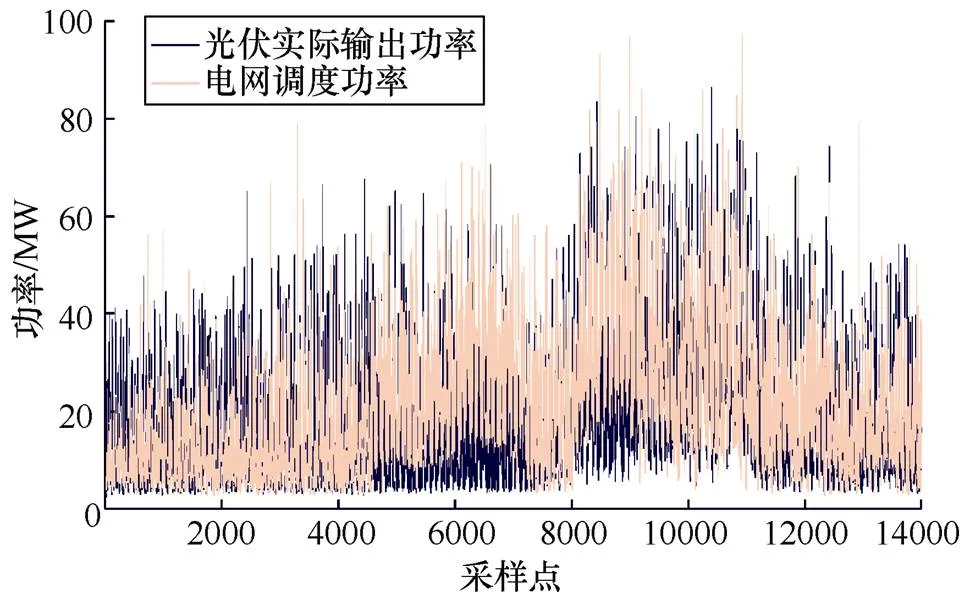
图4 光伏实际输出功率和电网调度功率

将光伏实际输出功率和电网调度功率做差，将差值作为混合储能系统参考功率，各时刻混合储能系统的工作状态如图5所示。

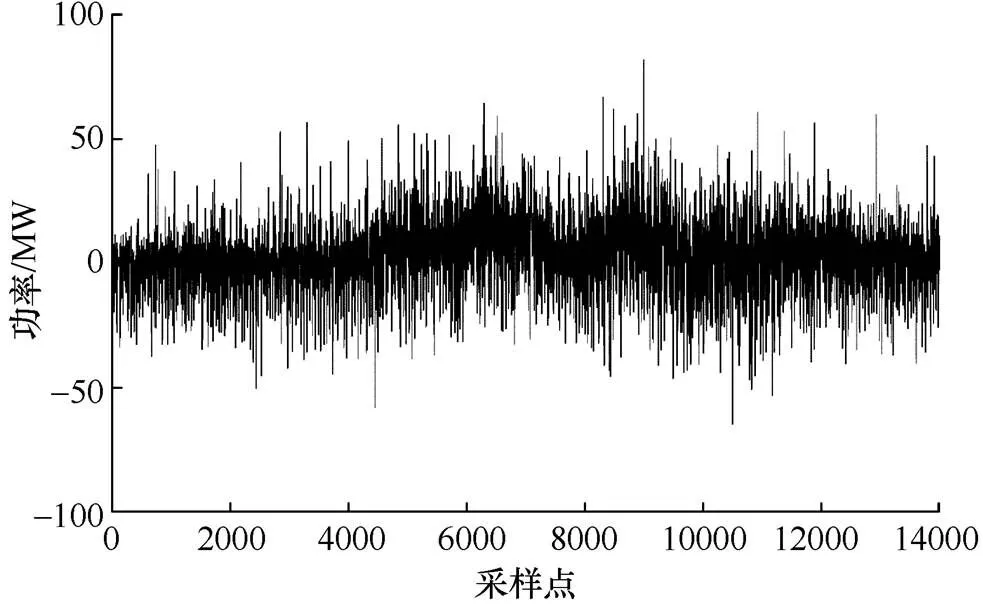
图5 混合储能系统工作状态

利用ELMD对混合储能系统参考功率进行分解，分解参数设定：添加白噪声的信噪比=0.2，添加白噪声的次数=100，采样频率为1Hz。得到频率范围由高到低的14个PF分量和1个余量，图6为PF分量及对应的幅频特性曲线，限于篇幅，本文仅列出部分PF曲线。之后对相邻两个PF分量作相关性分析：先对PF1、PF2作相关性评估（相关系数为cor1），再对PF2、PF3作相关性评估（相关系数为cor2），对剩余PF分量重复上述做法，此处不再赘述。相邻PF分量相关度变化趋势如图7所示，可以看出PF13和PF14之间呈极弱相关，耦合度极低，PF1和PF2相关程度次之，那么可将PF14及余量重构为蓄电池参考功率，则蓄电池主要工作频段为0～0.005Hz；PF1重构为超级电容参考功率，则超级电容主要工作频段为0.2～0.5Hz；PF2～PF13重构为氢储能系统参考功率，则氢储能系统主要工作频段为0.005～0.3Hz。

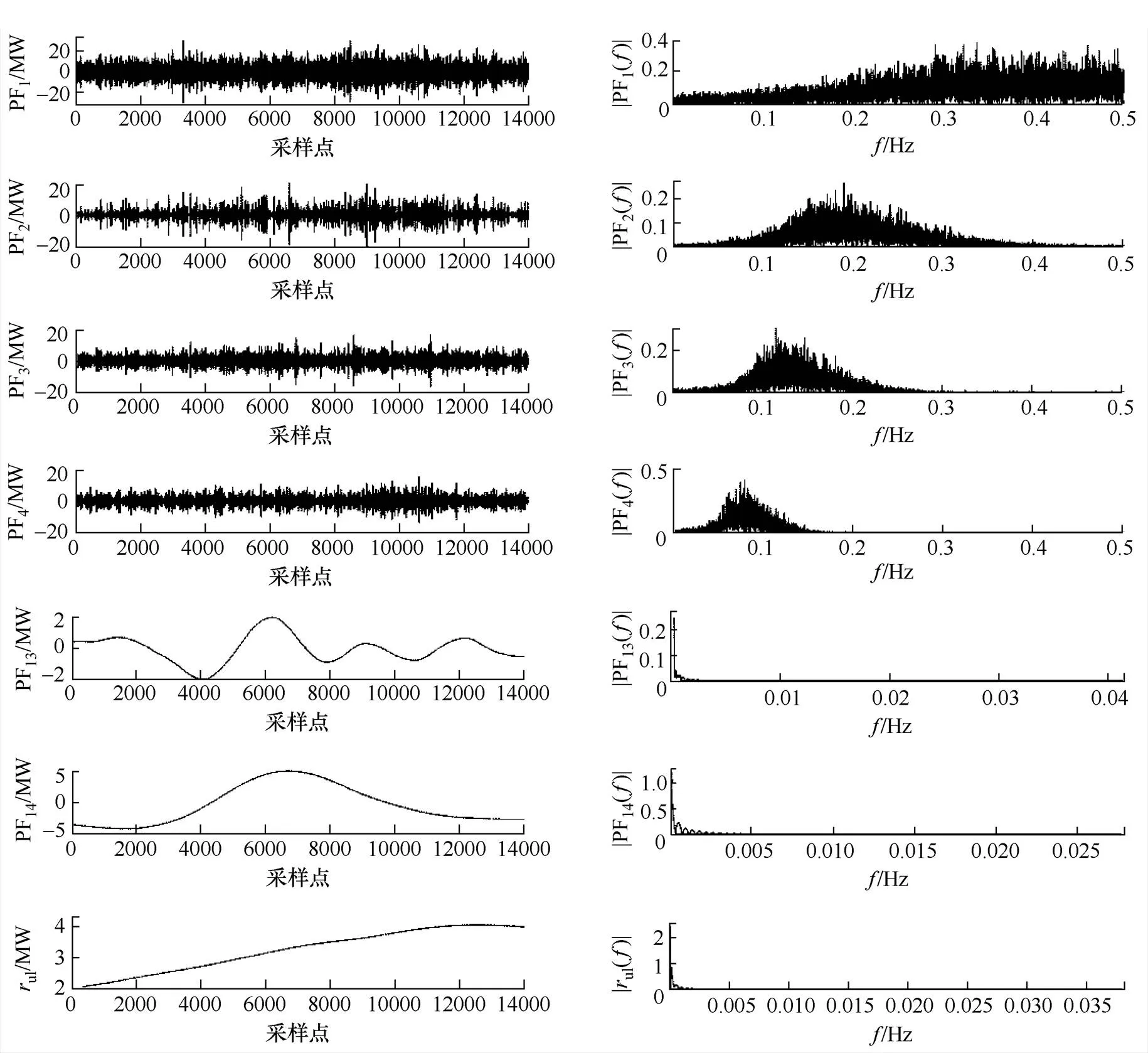
图6 ELMD分解得到的部分PF及对应的幅频特性曲线

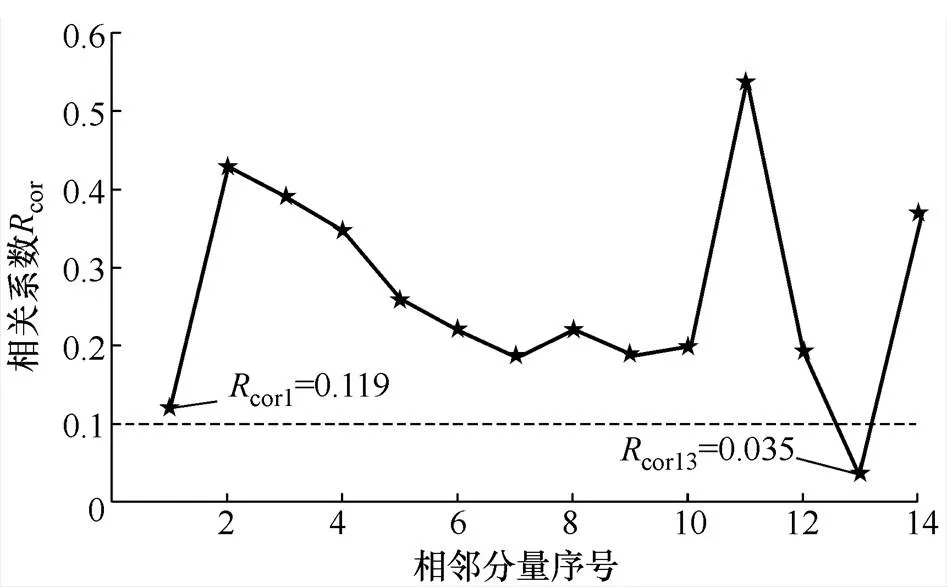
图7 相邻PF分量相关度变化趋势

超级电容、氢储能、蓄电池作为三种不同介质的储能装置，单一和混合配置在光伏发电侧的经济效益不尽相同。本文选用5种配置方案，储能系统技术参数见表2。方案1为配置单一超级电容储能系统；方案2为配置单一氢储能系统；方案3为配置单一蓄电池储能系统；方案4为配置超级电容和蓄电池组成的HESS；方案5为配置超级电容、氢储能、蓄电池组成的HESS，配置方法采用本文提出的ELMD-PPMCC功率分配法。5种方案优化配置结果见表3。方案5超级电容、氢储能、蓄电池的实时SOC如图8所示。

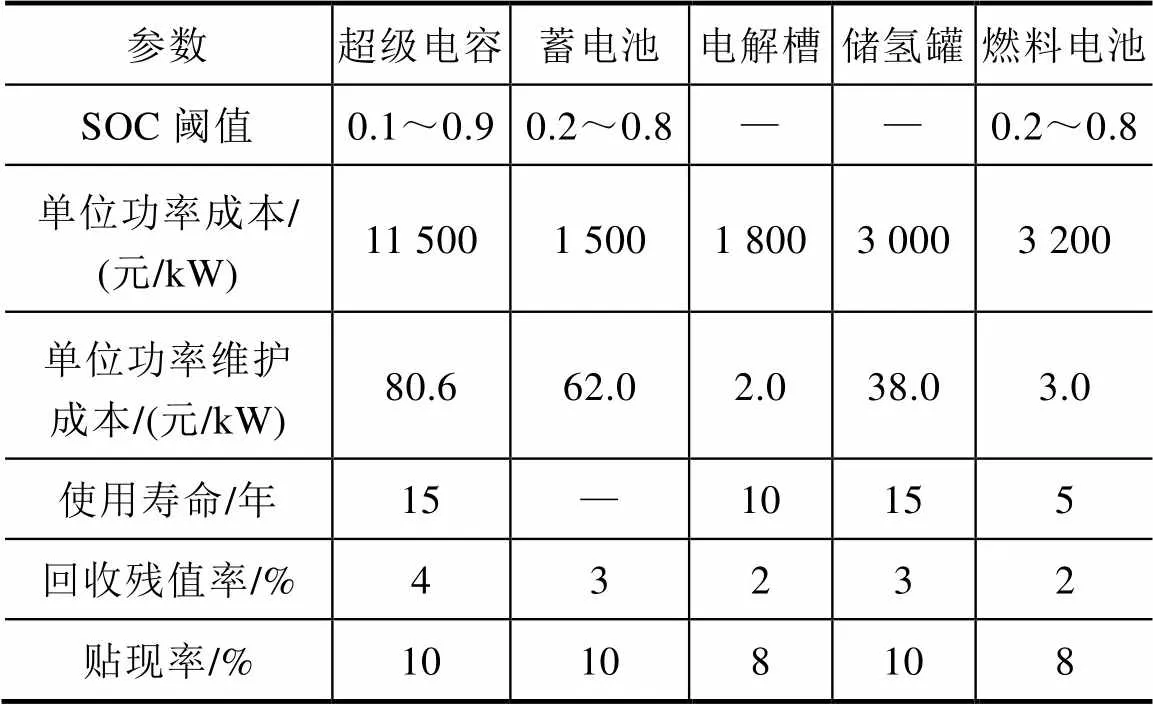
表2 储能系统技术参数

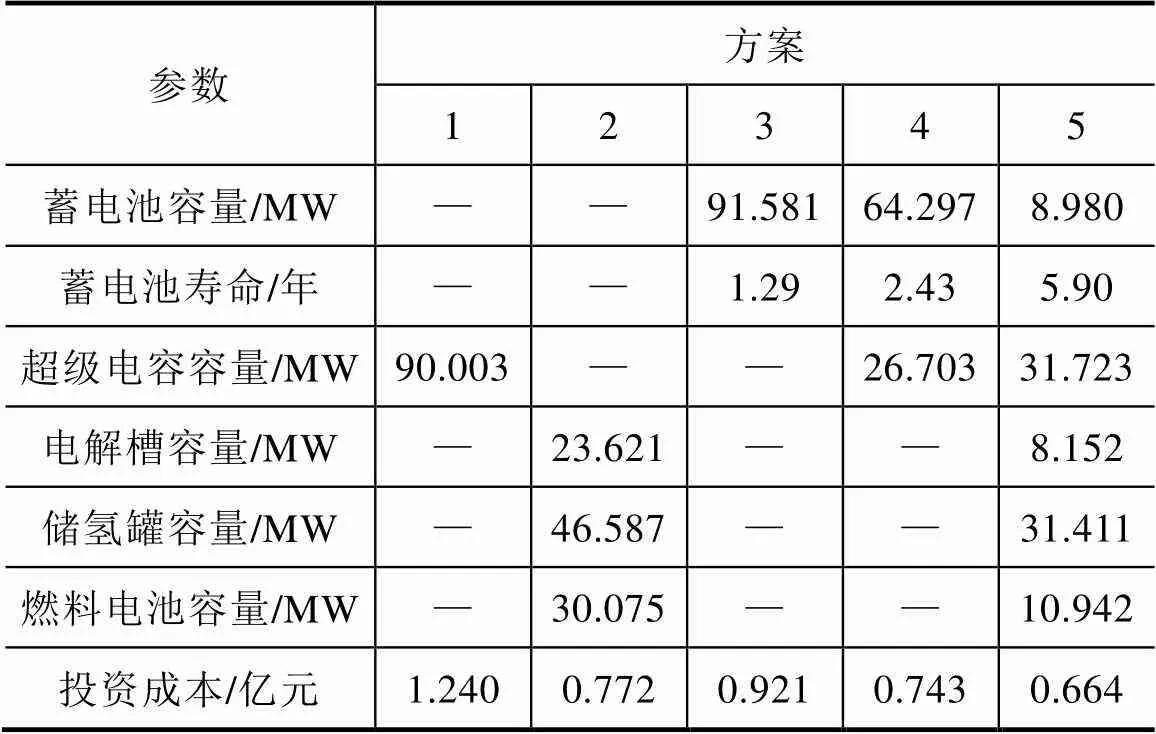
表3 储能优化配置结果

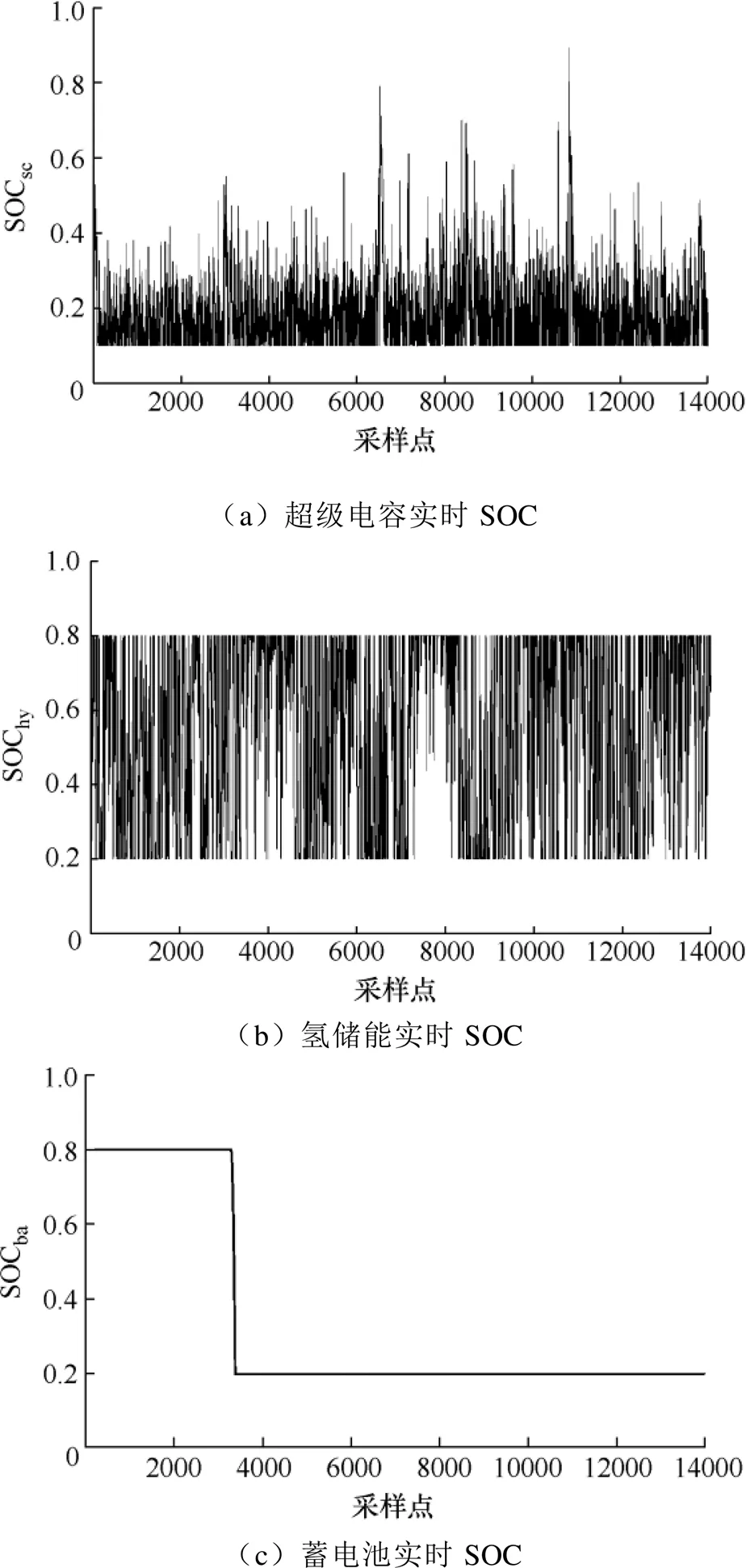
图8 方案5储能实时SOC

从图8可看出，本文方法对HESS功率进行分配后，HESS在与光伏发电协同运行时，超级电容和氢储能作为主储能工作，充放电频繁，两者中超级电容优先级更高，以放电为主，其SOC频繁达到下限；蓄电池作为辅助储能，在一次深度放电后待机，在主储能不能满足系统要求时才继续执行充放电指令。

从表3数据可知，在光伏发电侧配置单一储能，则储能系统的工作负担较大，尤其对于单一蓄电池储能，其循环寿命相比于HESS要减少许多，从方案5的5.9年到方案4的2.43年，方案3中蓄电池的循环寿命只有1.29年，这是因为蓄电池需要承担功率的最高频波动分量，这不仅会使蓄电池充放电频率变高，而且多次深度放电会使蓄电池加速老化，这样会增加蓄电池的更换次数，投资成本相应增高。若配置单一超级电容储能系统，则配置容量会相当高，目前超级电容属于高成本储能装置，并且其规模化应用还有待研究，在光伏发电侧只配置超级电容，无法带来良好的经济效益。若配置单一氢储能系统，由于目前氢储能的电转氢、氢转电效率低（约为60%～70%），能量转换过程相比于超级电容和蓄电池复杂，因此难以有效保证光伏发电的供电质量，而且氢储能商业化水平较低，技术还不够成熟。相比于超级电容和蓄电池组成的HESS，由超级电容、氢储能、蓄电池组成的HESS进一步减少了蓄电池的工作负担，提高了其使用寿命，减少了更换成本，且在主储能维护检修期间，蓄电池可以暂时作为主储能设备进行充放电工作，这样更加提升了电网对光伏的消纳能力，也进一步提高了光伏发电的可 控性。

6 结论

配置HESS能够提高电网对新能源发电的接纳能力。本文以某地光伏电站实际采样数据为例，建立了光伏发电-超级电容-氢储能-蓄电池的光伏HESS模型，在LMD基础上，利用ELMD分解HESS参考功率，结合超级电容、氢储能、蓄电池本体的特性，通过PPMCC寻找到两个储能工作频段分界点，将在不同频段波动的HESS功率有效地分配给三种不同的储能装置。经仿真分析发现，与单一储能装置相比，两种或两种以上不同介质的储能装置协同工作更具经济性优势，既提高了储能系统使用寿命，也降低了配置成本。本文方法可为光伏电站配置HESS提供技术参考和理论依据。

[1] 张俊涛, 程春田, 申建建, 等. 考虑风光不确定性的高比例可再生能源电网短期联合优化调度方法[J]. 中国电机工程学报, 2020, 40(18): 5921-5932.

[2] 李妍, 王洁, 王少荣, 等. 计及新能源特性的配电网评估指标及其隶属度函数的研究[J]. 电力系统保护与控制, 2018, 46(8): 43-49.

[3] 李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J]. 电力系统自动化, 2019, 43(8): 15-24.

[4] 刘畅, 卓建坤, 赵东明, 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J]. 中国电机工程学报, 2020, 40(1): 1-18, 369.

[5] 谢丽蓉, 郑浩, 魏成伟, 等. 兼顾补偿预测误差和平抑波动的光伏混合储能协调控制策略[J]. 电力系统自动化, 2021, 45(3): 130-138.

[6] 张晴, 李欣然, 杨明, 等. 净效益最大的平抑风电功率波动的混合储能容量配置方法[J]. 电工技术学报, 2016, 31(14): 40-48.

[7] 齐晓光, 姚福星, 朱天曈, 等. 考虑大规模风电接入的电力系统混合储能容量优化配置[J]. 电力自动化设备, 2021, 41(10): 11-19.

[8] 郑熙东, 江修波. 基于完备经验模态分解与能量熵的混合储能系统功率分配[J]. 电气技术, 2020, 21(11): 61-65, 70.

[9] 吴倩, 王洋, 王琳媛, 等. 计及波动平抑与经济性的风光储系统中混合储能容量优化配置[J]. 电测与仪表, 2022, 59(4): 112-119.

[10] SHARMA R K, MISHRA S. Dynamic power manage- ment and control of a PV PEM fuel-cell-based standalone AC/DC microgrid using hybrid energy storage[J]. IEEE Transactions on Industry Applications, 2018, 54(1): 526-538.

[11] 李瑞民, 张新敬, 徐玉杰, 等. 风光互补系统中混合储能容量优化配置研究[J]. 储能科学与技术, 2019, 8(3): 512-522.

[12] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.

[13] NOR N M, ALI A, IBRAHIM T, et al. Battery storage for the utility-scale distributed photovoltaic gener- ations[J]. IEEE Access, 2017, 6: 1137-1154.

[14] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.

[15] 黄大为, 齐德卿, 蔡国伟. 基于制氢系统的平抑风电输出功率方法研究[J]. 太阳能学报, 2016, 37(12): 3155-3162.

[16] HU Qiang, LIN Jin, ZENG Qing, et al. Optimal control of a hydrogen microgrid based on an experiment validated P2HH model[J]. IET Renewable Power Generation, 2020, 14(3): 364-371.

[17] 肖白, 刘健康, 张博, 等. 考虑阶梯碳交易和需求响应的含氢储能的并网型微电网优化配置[J/OL]. 电力自动化设备, DOI: 10.16081/j.epae.202204074.

[18] ZHANG Luyao, CHANG Jianhua, LI Hongxu, et al. Noise reduction of LiDAR signal via local mean decomposition combined with improved thresholding method[J]. IEEE Access, 2020, 8: 113943-113952.

[19] 王朝阁, 李宏坤, 杨蕊, 等. 基于自适应噪声参数优化ELMD的行星齿轮箱故障诊断研究[J]. 振动与冲击, 2020, 39(18): 60-69.

[20] 肖勇, 赵云, 涂治东, 等. 基于改进的皮尔逊相关系数的低压配电网拓扑结构校验方法[J]. 电力系统保护与控制, 2019, 47(11): 37-43.

[21] 罗煜, 黄梅, 鲍谚, 等. 基于储能SOC优化控制的风储电站实时跟踪发电计划控制策略[J]. 电工技术学报, 2016, 31(增刊1): 214-220.

[22] 傅晓梅, 温步瀛, 唐雨晨. 考虑电池储能运行特性的微网优化运行[J]. 电气技术, 2021, 22(4): 12-19.

[23] 肖浩, 裴玮, 杨艳红, 等. 计及电池寿命和经济运行的微电网储能容量优化[J]. 高电压技术, 2015, 41(10): 3256-3265.

[24] ZAKERI B, SYRI S. Electrical energy storage systems: a comparative life cycle cost analysis[J]. Renewable & Sustainable Energy Reviews, 2015, 42(2): 569-596.

Optimal configuration of electricity-hydrogen hybrid energy storage on photovoltaic generation side based on ensemble local mean decomposition and correlation analysis

LIU Yuchen YAN Qunmin GUO Yang LIU Xinyu SANG Xingyong

(School of Electrical Engineering, Shaanxi University of Technology, Hanzhong, Shaanxi 723001)

Intermittency and volatility of photovoltaic output still have great influence on power grid. Space-time translation of electric power by energy storage device can improve the controllability of photovoltaic power generation and improve the quality of power supply. In this paper, the capacity configuration method of hybrid energy storage system (HESS) composed of battery, super capacitor and hydrogen energy is proposed. Firstly, the mathematical models of photovoltaic power station and energy storage system are established. The difference between the dispatching power of power station and the actual output power of photovoltaic power generation is taken as the reference power of HESS. High, medium and low frequency components of HESS reference power are determined by ensemble local mean decomposition (ELMD) and Pearson product moment correlation coefficient (PPMCC). Under the constraint of the state of charge (SOC) of the three energy storage devices, the power of super capacitor, hydrogen energy storage and battery is allocated successively. The battery cycle life is considered, and the battery damage model is incorporated into the life cycle cost (LCC) assessment system of HESS. Finally, through the simulation of the actual scheduling data of a photovoltaic power station in Matlab, it is proved that the method can effectively decompose and reconstruct the HESS power according to different working frequency bands, and the advantages of HESS relative to single energy storage in economy and technology are reflected.

solar power; hybrid energy storage; ensemble local mean decomposition (ELMD); correlation coefficient; capacity configuration

国家自然科学基金面上项目（62176146）

2022-06-20

2022-07-09

刘语忱（1997—），男，陕西省西安市人，硕士研究生，研究方向为电力系统分析与电力储能技术。