基于H∞混合灵敏度的并网逆变器谐振控制策略

张 萍 沈新鹤

基于∞混合灵敏度的并网逆变器谐振控制策略

张 萍 沈新鹤

（兰州理工大学电气工程与信息工程学院，兰州 730050）

随着可再生能源及分布式发电相继并入电网，并网的电能质量问题备受关注。并网逆变器作为分布式发电和交流电网之间的连接枢纽，是解决电能质量问题的关键。为了减小逆变器输出电压电流的谐振，提出基于虚拟同步机算法的∞鲁棒控制策略。首先在系统性能要求的基础上，选取灵敏度加权函数来解决电网参数波动问题，建立并网逆变器系统数学模型及状态空间方程，最后通过求解代数黎卡提方程，得到∞控制器。在Matlab/Simulink仿真平台上，比较所提控制方法与传统PID控制方法、下垂控制方法，验证了所提控制方法应对电网参数变化、滤波器参数波动具有较强的鲁棒性。

并网逆变器；虚拟同步机；∞控制；谐振抑制

0 引言

分布式发电技术将可再生能源转化为电能接入电网使用，这在一些偏远地区显得尤为重要[1]。分布式电源作为备用电源，对主线路系统的可靠性起支持作用[2]。并网逆变器作为分布式发电与电网的接口，经常出现工作状态不稳定、故障率高的情况。为了使逆变器具有同步发电机故障穿越的特性，一些学者提出虚拟同步机与逆变器相结合的控制策略，即虚拟同步发电机（virtual synchronous generator, VSG）。

并网逆变器系统中的LCL型滤波器为三阶系统，在逆变器系统运行过程中，不同频段会产生谐振尖峰，由此引发电流电压波形的畸变，称此为谐振[3]。为使逆变器输出的电能质量满足要求，需要抑制并网逆变器的谐振，通常有以下五种方法：电流闭环控制方法、附加电阻或电容的无源阻尼方法、在控制回路附加虚拟电阻或电容的有源阻尼方法、基于间接采样的反馈控制方法、基于多变量组合反馈的有源阻尼方法。文献[3]采用滤波电感（电网侧）的电流值作为控制器的输入，用电流闭环控制实现对系统的谐振抑制。文献[4]针对并网损耗问题做了相应改进，在滤波电容中串联无源补偿器，以此来保持良好的并网电流质量。文献[5]增加谐振比例控制器，改变控制输入的参数结构，使控制输入不含相应频率的谐波。文献[6]在此前基础上采用多比例谐振控制器来抑制并网逆变器的谐振，主要集中在5次、7次、11次低频谐波。

在虚拟同步机系统模型分析中，大多采用小信号模型分析法[7]，通过小信号模型分析可以判断系统稳定与否，并得出系统的振荡点频率及引起振荡的状态变量和系统参数。文献[8]利用二阶系统的暂态指标，即峰值时间、最大超调量、调节时间来观察和设计控制系统的参数。文献[9-10]利用根轨迹法分析控制器设计过程中参数对系统的影响，为控制器设计提供重要参考。文献[11-12]从控制系统的状态方程误差入手，对系统模型的虚拟惯性和阻尼系数采用自适应律，提升参数的可调节范围。文献[13]通过对参数的不确定性建立摄动函数，求解出鲁棒控制器，提高了三相并网逆变器在一定范围内的稳定性和抗干扰性，但其在谐振抑制方面作用较小；其次，利用鲁棒控制器抑制系统结构变化，扩大了系统稳定区间，但在改善电流谐波畸变率（total harmonic distortion, THD）方面作用较小。

在并网逆变器运行过程中，电网的运行方式改变、电力负荷随不同季节、不同时间和用户生产流程的改变都会使电网阻抗发生变化，而电网阻抗的波动性和随机性、分布式能源的出力波动等不确定因素都会导致并网逆变器的输出不断变化，以上情况都属于控制对象参数的摄动问题[14]。鲁棒控制理论是设计一个固定的控制器，使具有不确定性的对象满足控制品质，常见的鲁棒控制理论有∞控制理论、结构奇异值理论等，本文选取∞控制理论。

由此，本文提出一种基于虚拟同步机的并网逆变器鲁棒控制方法，首先给出典型并网逆变器拓扑结构，构建基于虚拟同步机控制和S/R混合灵敏度函数的∞电网阻抗摄动数学模型；然后将并网逆变器谐振问题转换为标准∞混合灵敏度函数问题，并设计谐振鲁棒控制器；最后基于Matlab/Simulink仿真平台搭建并网逆变器仿真模型，对比不同情况下的电流畸变率来验证所提方法的正确性和有 效性。

1 三相并网逆变器系统模型

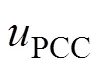
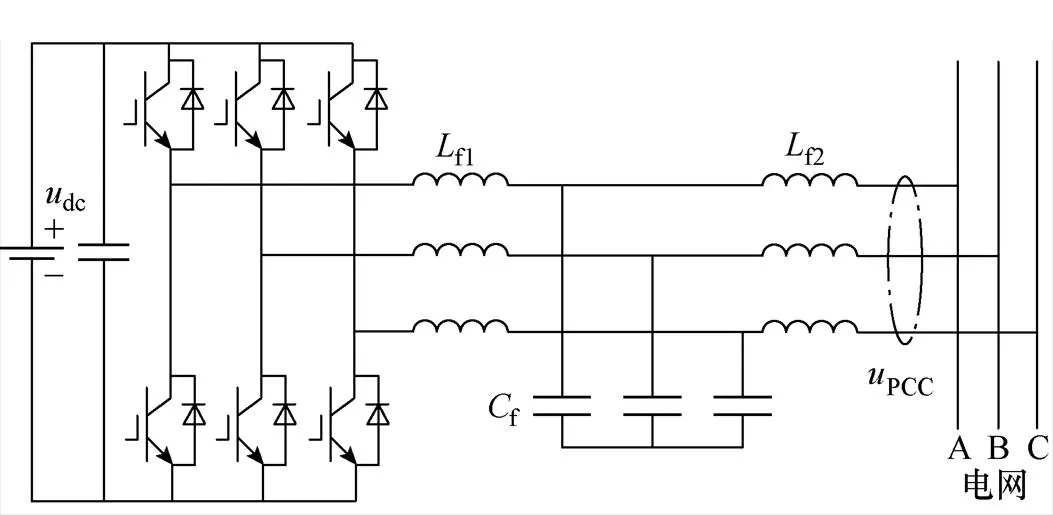
图1 并网逆变器系统结构

根据并网逆变器系统结构，分析其在三相坐标轴下的电压电流回路方程，确定并网逆变器系统在ABC三相坐标下的数学模型为

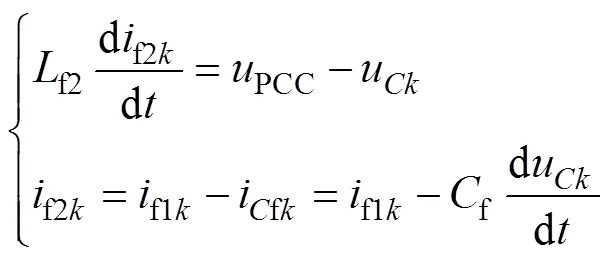
根据并网逆变器系统建立数学模型，忽略开关管阻抗，得出LCL滤波器标称系统在加入电网阻抗时的传递函数为

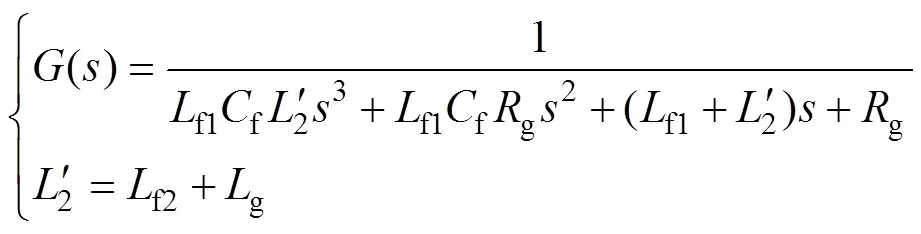
2 三相并网逆变器系统控制策略

本文选择电流源型虚拟同步机控制方法，即将逆变器视为虚拟同步发电机控制，同时结合有功功率获得参考相位、无功功率获得参考电压，然后加入虚拟阻抗环节、虚拟同步算法、鲁棒控制三部分来实现对并网逆变器的控制。VSG并网逆变器控制模型框图如图2所示。

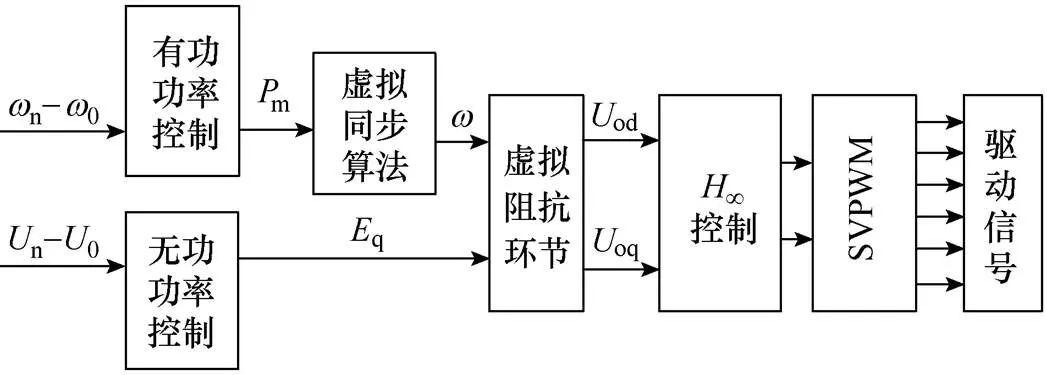
图2 VSG并网逆变器控制模型框图

通过虚拟同步机控制，可以使逆变器以惯性穿越故障区，如系统较大功率缺额和电网电压、频率过快波动等故障，以此保证并网逆变器系统的稳定运行。∞控制可以在一定范围内减少电网阻抗波动带来的影响。结合虚拟同步机控制和∞控制两种控制策略，可以扩大并网逆变器的稳定工作范围，获得良好的并网电能质量。

3 鲁棒控制器的设计

鲁棒控制是利用系统的无穷范数作为目标函数，求解∞控制器，同时用评价信号来表征控制性能。在实际的并网系统中，并网逆变器参数会存在不确定性，同时系统在运行过程中会受到来自电网阻抗波动、滤波器参数变化等外界干扰。在逆变器并网过程中，电网阻抗的摄动会引起谐波畸变率变化。

3.1 参数不确定性问题

以参数摄动与标称系统的奇异值作参考，求得参数的摄动范围，然后把参数摄动范围引入鲁棒控制的加性不确定性或乘性不确定回路中，由此设计出的鲁棒控制器可以适应电网阻抗的变化，具有强抗干扰性。

电网阻抗摄动会改变系统传递函数零极点的分布，因此选用乘性摄动模型解决系统零极点分布变化问题。乘性摄动模型描述为

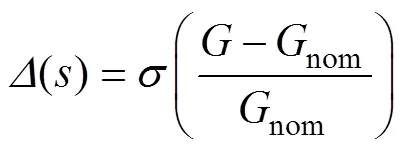
根据系统不确定性得出标称系统的表达式为

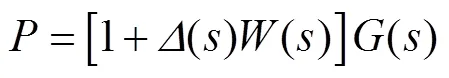
式中，为加权函数。

奇异值由奇异值分解得到，是将所给系统的传递函数形式转换为矩阵形式，后将矩阵分解成若干秩为1的矩阵，最后求和得出[15]。分解后的式子为

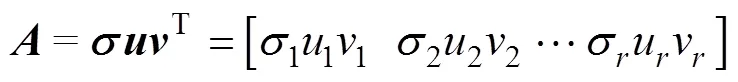
式中：为用矩阵形式表达的系统；=[12…]为奇异值向量；为奇异值个数；=[12…u]T和=[12…v]T分别为分解矩阵的两列向量。

参数摄动奇异值范围如图3所示。图3中，最上方虚线表示乘性摄动模型的奇异值，其下方的虚线表示模型参数摄动范围。当电网阻抗值高于8倍的电网侧电感值时，电网阻抗频率趋向于无穷大，所以电网阻抗上限值选为8倍电网侧电感值。通过乘性摄动模型，可以把一定范围内的参数摄动全部收敛其中，由此求解出的鲁棒控制器可以消除参数摄动带来的不稳定性。

图3 参数摄动奇异值范围

求得系统乘性不确定性的传递函数为

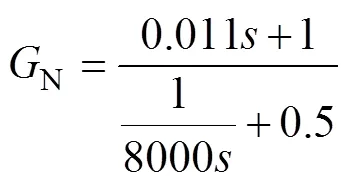
3.2 加权函数的选择

根据并网逆变器系统的结构，本文选择S/KS结构的混合灵敏度函数，如式（7）所示。

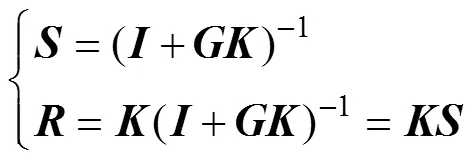
式中：为单位矩阵；为标称对象的状态空间实现；为控制器增益；灵敏度函数表示干扰到输出的传递函数；灵敏度函数表示参考到控制输入的传递函数。

根据标准鲁棒控制器的设计原理，加入S/KS问题后，得到系统的控制结构如图4所示。

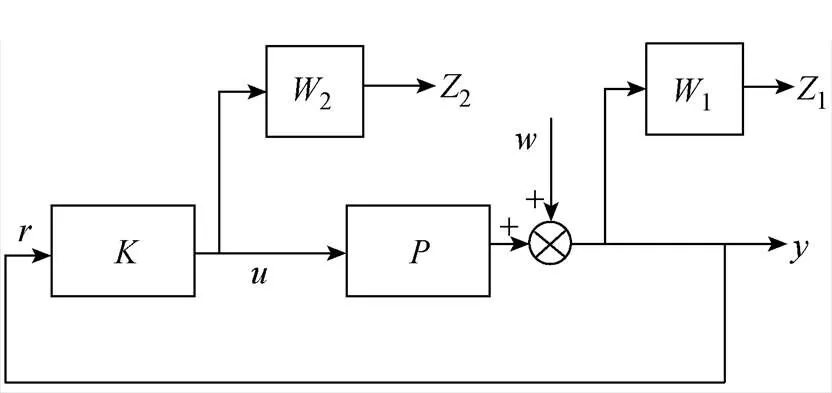
图4 加入S/KS问题后系统的控制结构

图4中，为标称控制对象；为求解的控制器增益；为参考输入；为控制输入；为外界干扰；为输出；加权函数1可以有效地抑制干扰；加权函数2可以限制控制量的大小；1和2为系统输出的评价函数，反映系统的性能指标。

S/KS问题的性能指标为

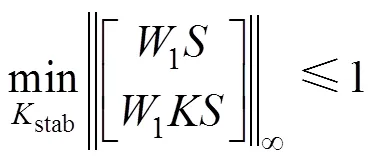
式中，stab为控制系统稳定时的增益。

S/KS问题就是如何确定系统的加权函数1、2，在S/KS问题结构中，是控制对象，包含了标称对象和乘性不确定的系统，控制对象表达式为

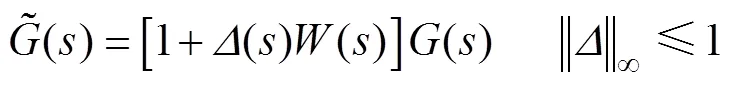
混合灵敏度加权函数的选取决定了系统的鲁棒性，是设计该谐振控制器的关键。为了使系统具有较强的鲁棒性，同时减小跟踪误差，加权函数1应设计为高增益低通滤波器，因此把电网频率值作为1加权函数衰减的转折点；2可以限制控制量的大小，防止系统在实际运行过程中过饱和而造成开关管的损耗严重，可以选择较小的常数值，本文选取的加权函数为

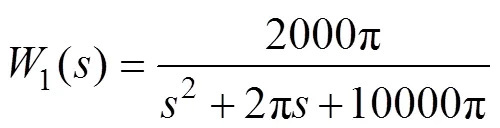
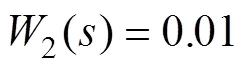
根据已确定的灵敏度函数和标称系统，可得基于混合灵敏度的∞问题的数学模型为

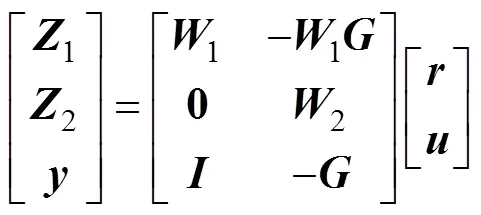
在三相对称情况下，建立并网逆变器的状态空间方程为

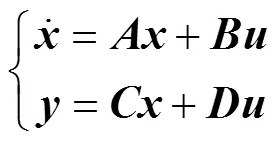
其中

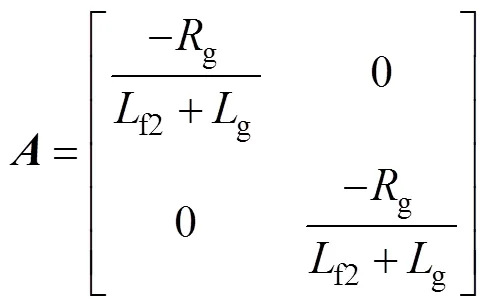
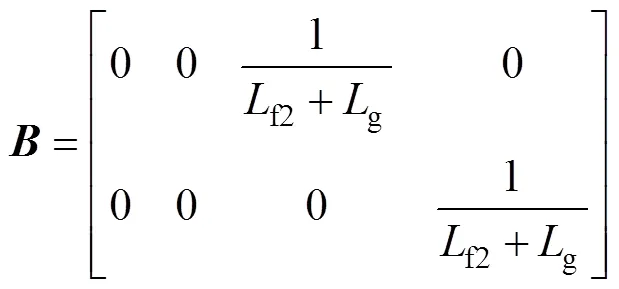
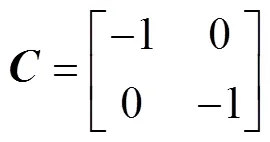
3.3 鲁棒控制器的求解

根据并网逆变器系统的状态空间模型表达式（13）～式（16）和S/KS问题的加权函数式（10）和式（11），通过Matlab鲁棒控制工具箱求解黎卡提方程得到六阶的∞鲁棒控制器为

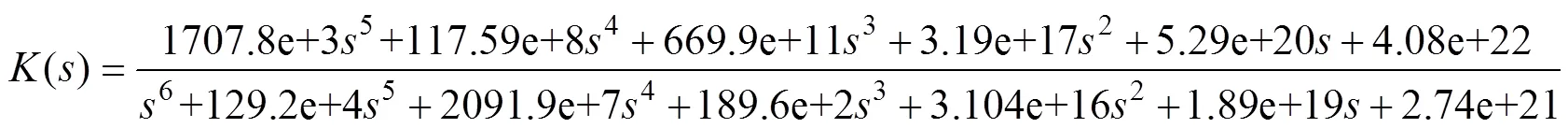
通过Matlab鲁棒控制工具箱中reduce函数降阶后，得到鲁棒控制器为

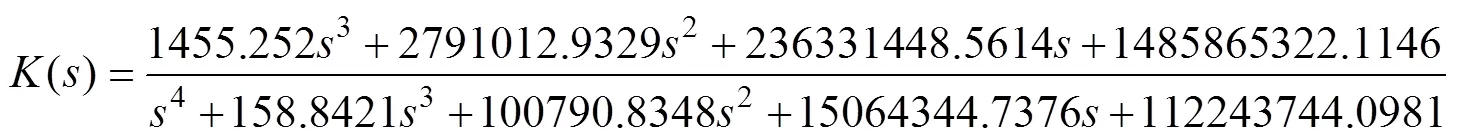
降阶后得到的鲁棒控制器为四阶。

4 仿真分析

为了验证控制策略的有效性，在Matlab/Simulink中根据图2搭建并网模型，仿真参数见表1。

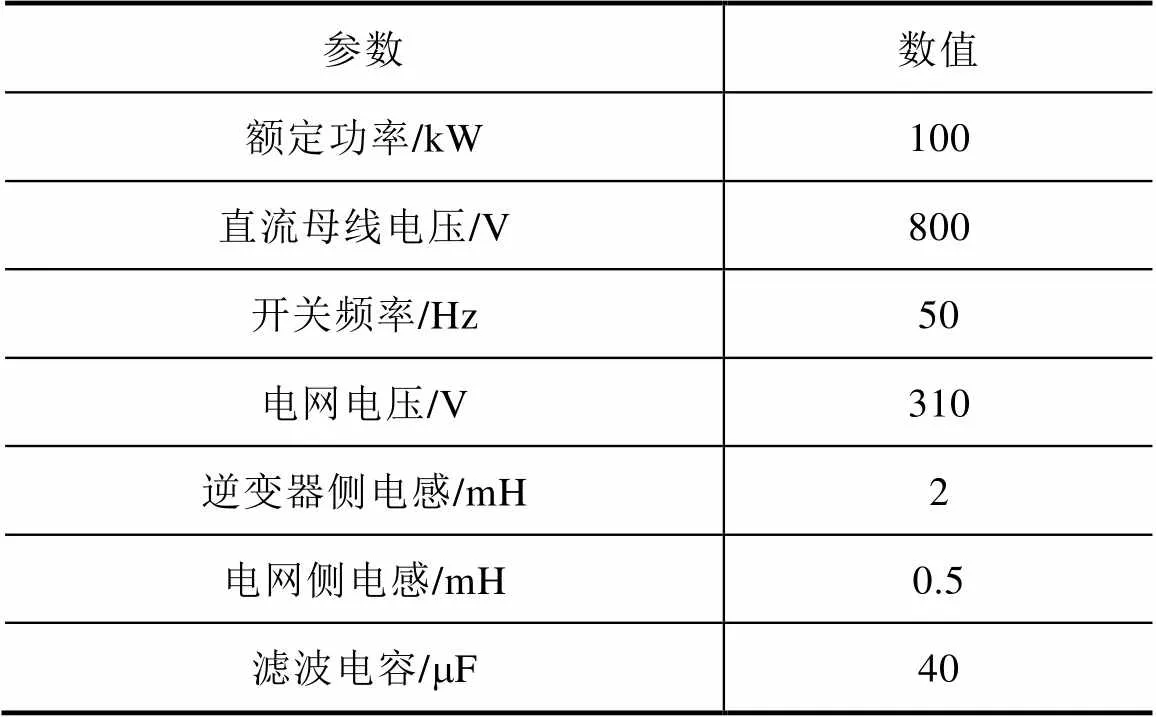
表1 仿真参数

在并网时，电压电流初始较小，系统达到稳定运行需要0.2s。在VSG控制策略下仿真，忽略电网阻抗，电流畸变率符合并网标准。无电网阻抗时，电流畸变率变化如图5所示。如果电网阻抗波动较大，这时电流畸变率超出5%，而并网电压畸变率变化较小，所以这里主要对并网电流做分析对比。在虚拟同步机控制环后加入∞鲁棒控制来保证系统的抗干扰性和稳定性。

在经典控制理论中，比例积分微分（proportional integral derivative, PID）控制是应用最广泛的控制策略，这里用并网输出电流和参考值的误差经过PID控制来抑制逆变器谐振。下垂控制是类似于发电机的下垂特性曲线得出的控制方式，在近几年系统维稳中受到关注；传统的VSG控制只能使系统穿越故障点，并不能改善并网电流的畸变率，所以本文改变控制模型图2中∞控制，分别替换为下垂控制、PID控制两种方式，得到三种控制方式下电流THD变化如图6所示。

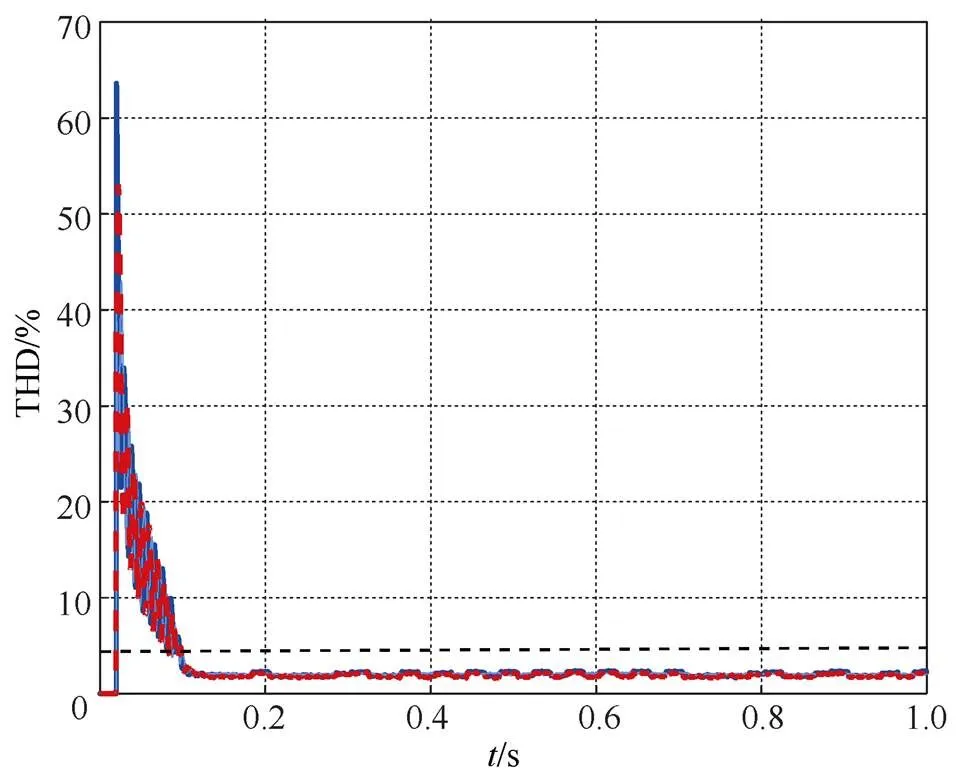
图5 无电网阻抗时，电流畸变率变化

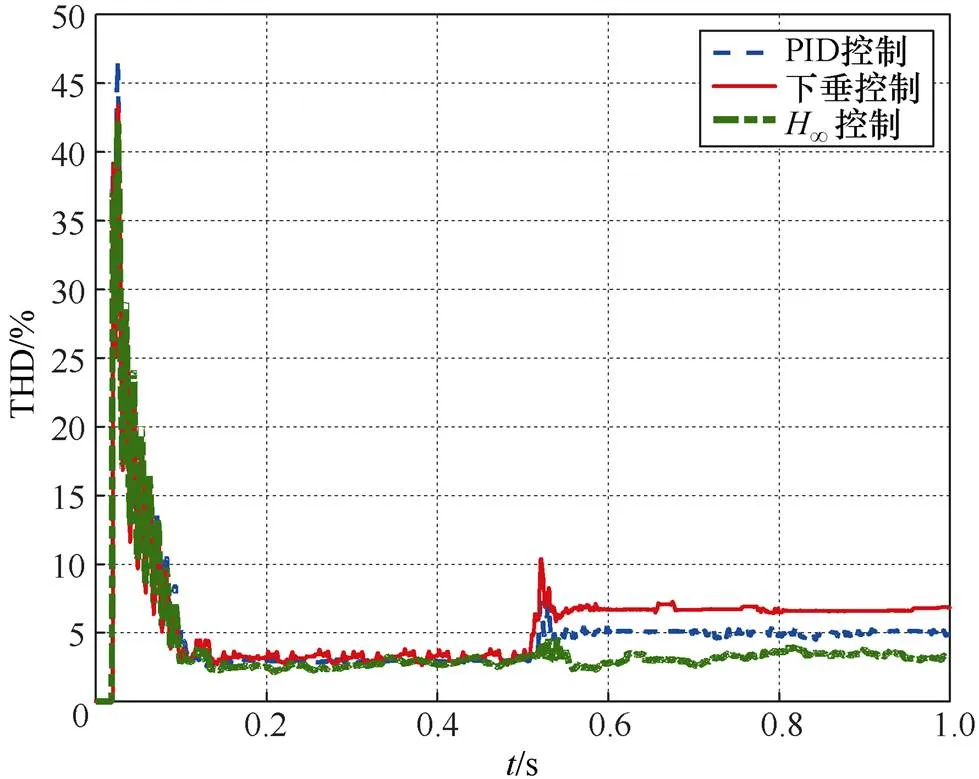
图6 三种控制方式下电流THD变化

在并网逆变器工作时，0.5s后电网加入最大的阻抗值，PID控制和下垂控制方式下的电流THD发生了跳变，且不能维持初始值，由初始值4%增加到5%～7%左右，已经不符合并网电流THD的标准（5%）。本文设计的∞控制器可以维持电网阻抗波动前后的电流THD，在0.5s前后没有太大变化。图7为三种控制方式下，系统稳定后的部分电流波形。

通过快速傅里叶变换（fast Fourier transform, FFT）分析，得到特定频段的THD。三种控制方式的FFT分析分别如图8～图10所示。

在加入电网阻抗后，PID控制可以基本维持电流的THD在5%左右，下垂控制输出的电流THD已经不符合并网电能质量标准。通过三种控制策略的对比可知，鲁棒控制可以减小不同频段的谐波畸变率，提高了并网逆变器输出电能质量。

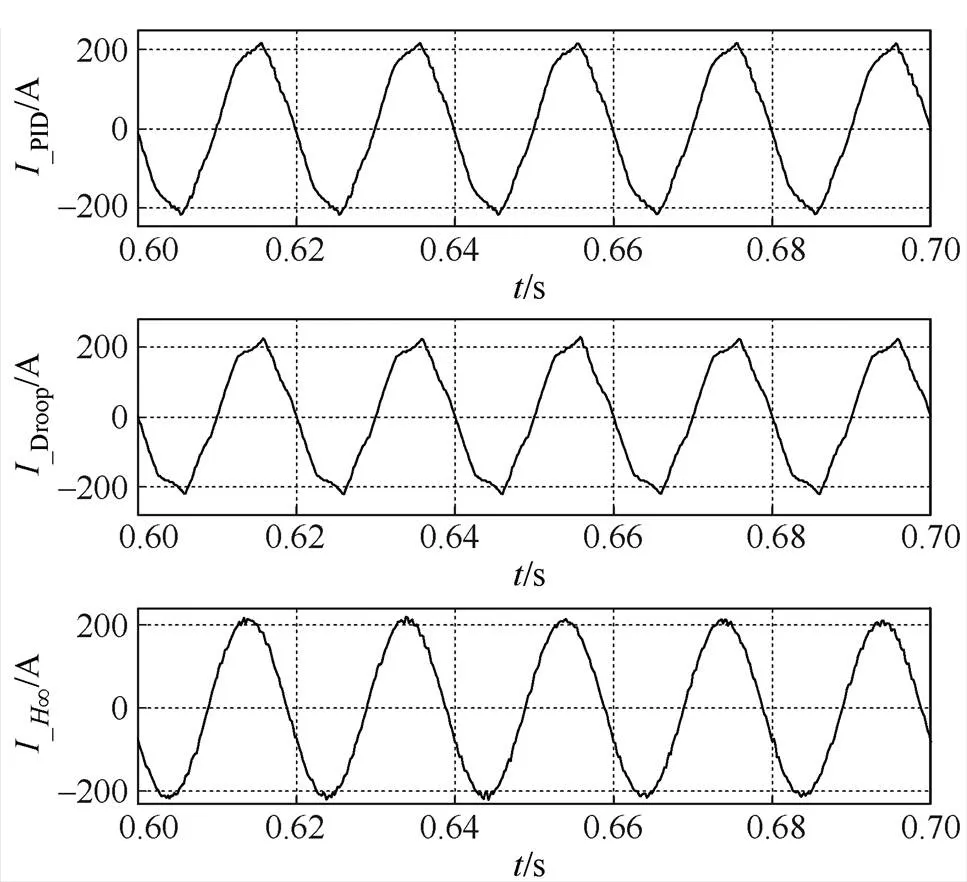
图7 三种控制方式下系统稳定后的部分电流波形

图8 PID控制，FFT分析

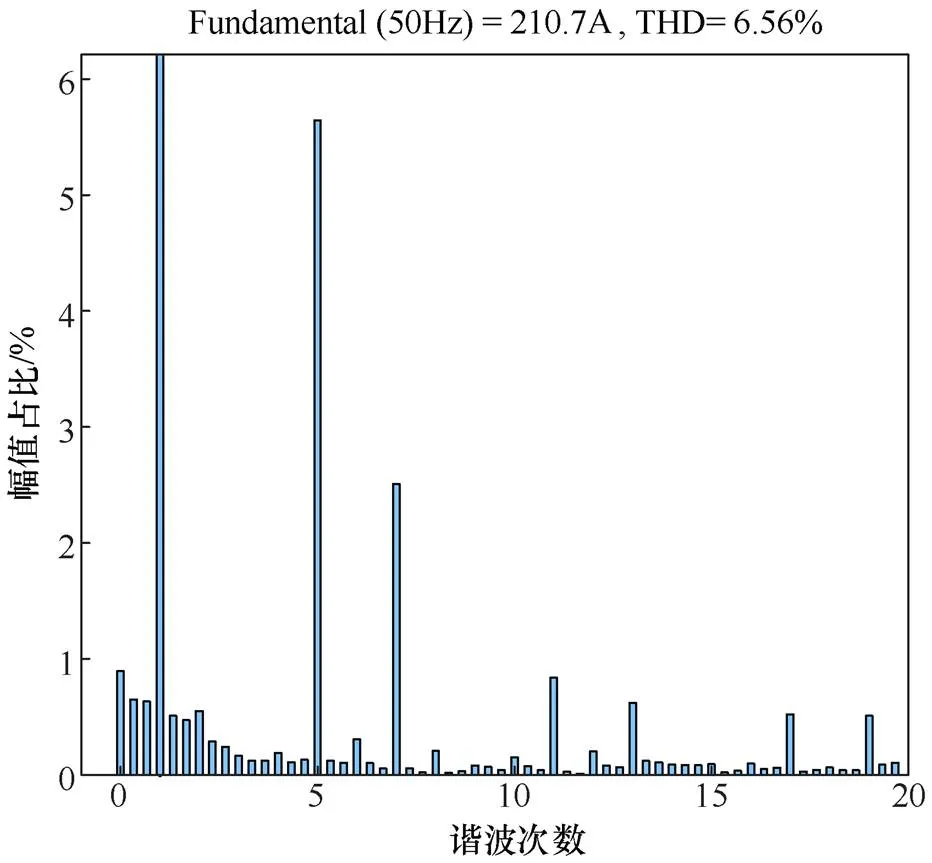
图9 下垂控制，FFT分析

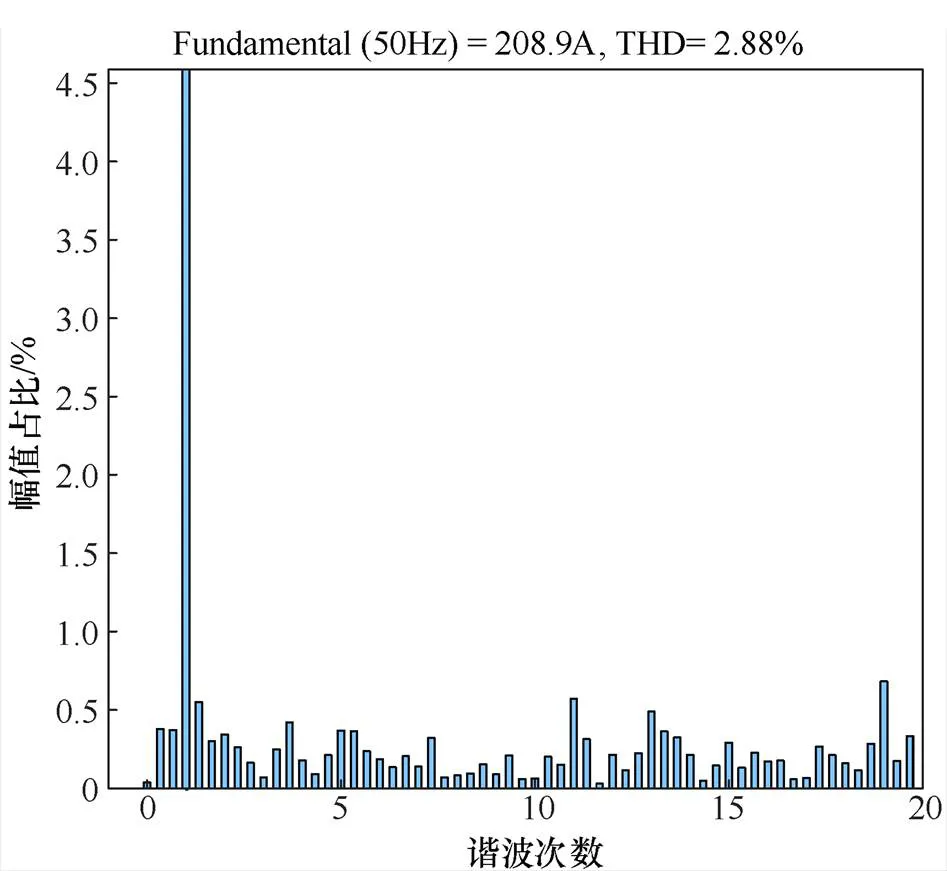
图10 H∞控制，FFT分析

5 结论

本文针对并网逆变器的谐振抑制问题，提出了一种基于虚拟同步机和S/R混合灵敏度函数的控制方法，能够维持并网逆变器输出电流电压畸变率的稳定。通过建立并网逆变器系统在VSG基础控制下的电网阻抗摄动数学模型，结合混合灵敏度函数，设计了谐振鲁棒控制器，有效降低了系统的谐波畸变率。通过仿真结果表明，在电网阻抗摄动时，该控制方法能有效地抑制并网逆变器的谐振，保证并网逆变器输出电流THD在允许的合理范围之内。为更好地分析谐振鲁棒控制器在并网时的作用，后续将开展谐振鲁棒控制器在多台逆变器并联情况下的研究工作。

[1] 史明亮. 探析新能源发电与分布式发电及其对电力系统的影响[J]. 现代制造技术与装备, 2021, 57(9): 84-85.

[2] 周美权, 徐晔, 黄克峰, 等. 虚拟同步发电机带脉冲负载运行特性研究[J]. 电气技术, 2022, 23(6): 59-68.

[3] 王立娜, 谭丽平, 徐志强, 等. 电池储能抑制直流配电网振荡的控制策略研究[J]. 电气技术, 2022, 23(6): 42-48.

[4] 马琳, 金新民, 唐芬, 等. 三相并网逆变器比例谐振控制及其网压前馈问题分析[J]. 电工技术学报, 2012, 27(8): 56-63.

[5] 郭磊磊, 金楠, 李琰琰, 等. 并网逆变器无电网电压传感器模型预测控制[J]. 电工技术学报, 2020, 35(12): 2612-2622.

[6] 刘倪. 基于小信号模型的虚拟同步机稳定性机理及参数整定研究[D]. 成都: 电子科技大学, 2019.

[7] 宫晶赢, 丁惜瀛, 毕明涛. 基于虚拟领导者一致性的大规模微电网智能协同分层控制[J]. 电气技术, 2022, 23(4): 42-47.

[8] 王博. 基于虚拟同步发电机的微网逆变器控制策略研究[D]. 徐州: 中国矿业大学, 2020.

[9] CHEN Junru, LIU Muyang, GUO Renqi, et al. Co- ordinated grid forming control of AC-side-connected energy storage systems for converter-interfaced generation[J]. International Journal of Electrical Power and Energy Systems, 2021, 133: 107201.

[10] 夏晋. 三相并网逆变器下垂控制与VSG控制对比分析研究[D]. 杭州: 浙江大学, 2020.

[11] YIN Jun. Influence of reactive power support con-trol strategy on short-circuit current calculation and fault analysis method of DFIG[J]. Energy Reports, 2021, 7: 5933-5942.

[12] 孙永豹. 基于虚拟同步机的微网系统逆变器控制策略研究[D]. 无锡: 江南大学, 2021.

[13] TENG Qingfang, XU Guorong, ZHENG Xuewei, et al. A novel sliding mode observer-based com-pound sliding mode current control with active damping for single phase grid-tied inverter system in weak grid[J]. International Journal of Electrical Power and Energy Systems, 2022, 141: 108117.

[14] ZHAO Ziyi, WANG Tianzhen, BENBOUZID M. A fault- tolerant reconfiguration system based on pilot switch for grid-connected inverters[J]. Microelectronics Reliability, 2022, 131: 114511.

[15] 沈睿佼, 杨洪耕, 吴昊. 基于奇异值总体最小二乘法的间谐波估计算法[J]. 电网技术, 2006, 30(23): 45-49.

Resonance control strategy of grid connected inverter based on hybrid sensitivity

ZHANG Ping SHEN Xinhe

(College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050)

With the successive integration of renewable energy and distributed generation into the power grid, the power quality of grid-connected power has attracted much attention. As the connection hub between distributed generation and AC grid, the grid-connected inverter is the key to solving the problem of power quality. In order to reduce the resonance of inverter output voltage and current, a∞robust control strategy based on virtual synchronous machine algorithm is proposed. Firstly, on the basis of system performance requirements, the sensitivity weighting function is selected to solve the problem of grid parameter fluctuation, and the mathematical model and state space equation of the grid-connected inverter system are established. Finally, the∞controller is obtained by solving the algebraic Riccati equation. Compared with the traditional PI control method and the droop control method on the Matlab/Simulink simulation platform, it is verified that the method proposed in this paper has strong anti-interference and stability in response to changes in grid parameters and filter parameter fluctuations.

grid-connected inverter; virtual synchronous machine;∞control; resonance suppression

2022-07-06

2022-08-06

张 萍（1979—），女，博士，副教授，研究方向为新能源发电建模与分析、电力电子技术开发与应用。