基于改进遗传模拟退火算法的分布式光伏储能投资决策研究

樊晓伟，王瑞妙，朱小军，姚 龙，周兴华，张 晓，4

（1.国网重庆市电力公司，重庆 400014；2.国网重庆市电力公司电力科学研究院，重庆 401123；3.北京中恒博瑞数字电力科技有限公司，北京 100085；4.华北电力大学电气与电子工程学院，河北 保定 071003）

0 引言

随着国家“双碳”提出实施，光伏发电装机容量和发电量不断攀升。光伏发电出力具有明显的波动性，影响了配电网的安全稳定运行。合理配置储能装置，可以抑制光伏发电出力波动，同时提高供电质量。文献[1]指出，储能电站可有效平抑高渗透分布式光伏出力波动，但未给出储能电站容量配置方法。文献[2]从经济效益最大角度，综合考虑分时电价、负荷转移、光伏出力不确定性等因素，构建光储微电网容量优化模型，但未考虑电压偏差、出力波动等电网安全稳定因素。文献[3]从成本效益最优角度提出含光伏发电配电系统的分布式储能（Distributed Energy Storage，DES）规划研究。文献[4]提出了一种光伏-储能系统协同控制策略。文献[5]提出了含高比例光伏出力区域的分布式储能的选址和容量分配方案。文献[6]针对配电网分布式光伏渗透率不断提高，提出了基于用户负荷特性的分布式储能容量配置策略，但未给出新建光伏电站的选址定容方法。文献[7]提出了基于光储联合系统的微电网整体解决方案，但未给出新建光伏电站和储能系统的联合投资决策方法。文献[8]提出一种考虑经济性的用户光伏—储能系统容量配置方法，但未考虑平抑光伏出力波动性。

针对现有方法的不足，本文提出一种基于改进遗传模拟退火算法的分布式光伏储能投资决策方法，以光伏电站投资经济效益最大化为目标，采用改进遗传算法确定分布式光伏安装位置和容量；在满足光伏出力波动约束条件下，以储能容量最小为目标，确定储能安装位置和容量。该方法不仅实现了光伏电站投资效益最大化，而且能够保障配电网安全稳定运行。

1 方案整体框架

方案整体框架见图1。具体流程如下：①基于地区光伏电站历史发电功率数据集，采用改进的K中心点聚类算法提取光伏出力典型场景；②考虑负荷、光伏出力时序特性，构建光伏、负荷联合时序场景；③从场景发生概率角度出发，充分考虑光伏安装运维成本、售电、节能降损效益，以光伏电站经济效益最大化为目标，采用改进遗传模拟退火算法确定分布式光伏位置选址和容量；④采用超级电容平抑分布式光伏发电出力波动，以容量最小为目标优化储能装置充放电功率曲线，进而确定储能安装位置和容量。

图1 解决方案整体流程Fig.1 Overall flow chart of the solution

2 基于改进的K中心点算法光伏出力场景缩减

聚类法通过将具有一定相似度的曲线聚为一类进行场景缩减，以精简数据、减少计算量。文献[9]采用k-means对全年风电、光伏、负荷数据进行聚类，用于电力系统中长期规划。本文采用基于动态时间弯曲距离的K中心点算法将分布式光伏出力曲线数据进行有效聚类，在保证风电分布特性的前提下减少场景数量。

在聚类分析中，需要评估各对象之间相似或不相似程度。距离是评估各对象之间相似程度常用的计算方法，距离越小相似程度越高。用户负荷曲线作为一种高维数值属性对象，选择一种合适的距离计算方法是聚类分析的关键。

假设有两条时间序列A={a1，…，ai，…，am}和B={b1，…，bj，…，bn}，m和n分别表示A和B的长度，动态时间弯曲（Dynamic Time Warping，DTW）首先构造一个m×n的矩阵M，元素M（i，j）为ai与bj之间的距离；然后在矩阵中寻找一条使两条序列间累积距离最小的弯曲路径W，W={w1，…，wk，…，wK}是M的一组连续的元素集合，并且满足以下约束。

①有界约束：max（m，n）≤K≤m+n-1。

②边界约束：元素w1=M（1，1）和wk=M（m，n）分别为弯曲路径的起点和终点。

③连续性约束：给定元素wk=M（i，j），其相邻元素wk-1=M（i＇，j＇）需满足i-i＇≤1，j-j＇≤1，即弯曲路径元素是相邻的。

④单调性约束：给定元素wk=M（i，j），其相邻元素wk-1=M（i＇，j＇）需满足i-i＇≥0，j-j＇≥0。

矩阵M中存在多条满足上述约束条件的弯曲路径，但是时间序列A和B的DTW距离是最小的弯曲路径[10]，[11]。弯曲路径采用动态规划算法求解，其最优解子结构为

因此，上述时间序列A和B的DTW距离为Ddtw（A，B）=d（m，n）。与欧氏距离相比，DTW距离不仅能反映两个序列之间的距离，而且能反映二者之间的变化趋势。

图2为额定功率为2 MW光伏发电的日功率曲线。某日发电功率1与其他发电功率曲线的距离如表1所示。

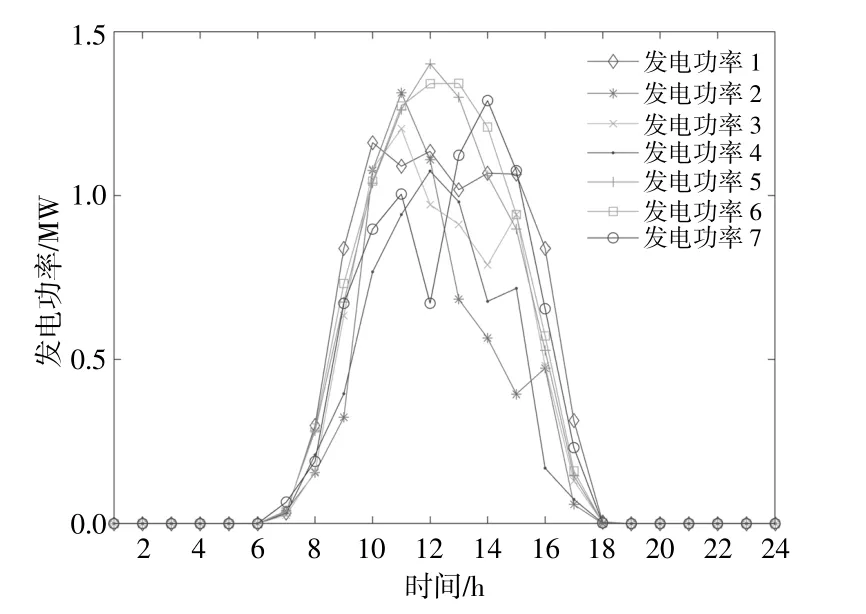
图2 光伏发电日功率曲线Fig.2 Daily power curve of photovoltaic

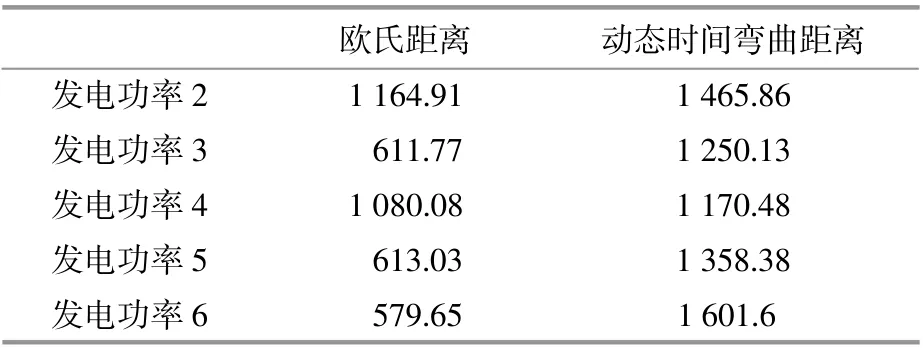
表1 发电功率1与其他发电功率距离Table 1 Distance between generating power 1 and other generating power

由表1可以看出：发电功率1与发电功率6的欧氏距离最小，但是相似性最差；动态时间弯曲距离大，能够捕获光伏发电日功率曲线之间的相似度。本文采用动态时间弯曲距离计算风-光-荷曲线之间的距离（相似性）。

当光伏出力场景缩减时，首先采用动态时间弯曲距离计算不同曲线之间的相似度，构建光伏出力曲线相似度矩阵；然后采用基于动态时间弯曲距离的K中心点聚类算法开展光伏发电曲线的聚类分析，各个聚类簇的中心点即为光伏出力的典型模式[12]，[13]。

3 基于改进遗传算法的分布式光伏规划

3.1 目标函数

从考虑多因素多角度出发，将电网公司投资光伏电站投资效益最大化作为选址定容模型，进行配电网光伏的布点定容规划，其中包括光伏电站投资费用、运行维护费用、光伏发电电费收益以及节能降损效益。具体模型为

式中：Btol为光伏发电总收益；Seg为光伏发电售电收益；CPV为分布式光伏设备投资安装费用；Cyun为分布式光伏的运维费用；ΔCloss为光伏安装发电节能降损效益；Pi为第i个光伏负荷联合时序场景发生概率；m为光伏负荷联合时序场景数量。

式中：n为光伏接入电网的节点个数；SPVi为节点i的光伏安装容量；CPVe为单位容量光伏的设备成本；CPVi为单位容量光伏的安装成本；CPVy为每年单位容量光伏的运维费用；mPV为光伏的投资回收期；r为贴现率；Ji为节点i的售电价；Pij为节点i第j年的发电量；Jbuy为上网电价购电价；Ploss为光伏安装前配电网每年电网损耗；Plosspv为安装光伏后的电网损耗。

3.2 约束条件

等式约束条件：

式中：PGi，QGi分别为节点i系统有功功率、无功功率；PDGi，QDGi分别为节点i分布式电源有功功率、无功功率；PLi，QLi分别为节点i负荷有功功率、无功功率；Ui，Uj分别为支路首末节点i和j的电压幅值；θij为以i和j为首末节点的支路电压相角差；Gij，Bij分别为支路的电导、电纳。

不等式约束条件如下。

①支路有功功率约束

式中：Pi为支路i的有功功率；Pimax为支路i允许的最大有功功率。

②分布式电源运行约束

式中：PDGi，min和PDGi，max分别为DG接入的最小限制、最大限制有功功率；PDGi为i点的DG接入有功功率。

③节点电压约束

式中：Vimin和Vimax分别为节点i最小允许电压和最大允许电压；Vi为节点i的电压值。

④光伏安装总容量约束

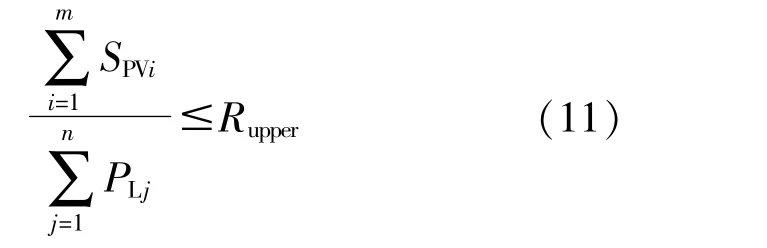
式中：m为光伏接入电网的节点个数；n为规划地区配电网用电负荷个数；PLj为节点j的用电负荷功率；Rupper为规划地区分布式光伏容量渗透率的上限。

3.3 基于改进遗传算法的光伏选址定容

求解包含大量决策变量和约束条件的配电网规划决策问题，通常需要启发式优化算法。本文采用改进自适应遗传模拟退火算法开展分布式光伏选址定容。

①适应度函数。分布式光伏规划的目标是使光伏电站投资经济效益最大化，构造的适应度函数为

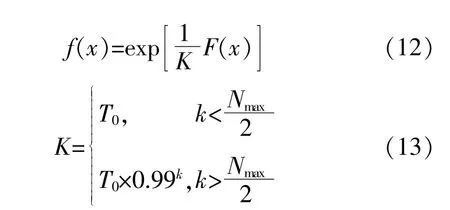
式中：f（x）为个体的适应度函数；F（x）为个体的目标函数，即光伏电站投资经济效益；T0为模拟退火问题的初始温度；Nmax为最大迭代次数；k为当前迭代次数。

②染色体编码。分布式光伏安装位置和安装容量属于离散变量，采用十进制整数编码为

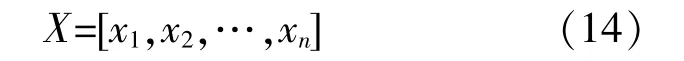
式中：xi=0，表示节点i不安装光伏；xi=m，表示节点安装m个单位容量光伏，1≤i≤n。

③选择操作。随机选取两个个体，比较二者的适应度，保存适应度较高的个体；将当前群体中适应度最高的个体直接复制到下一代。

④自适应交叉和变异操作。当群体有陷入局部最优解趋势时提高pc和pm；当群体在解空间发散时相应的降低pc和pm。

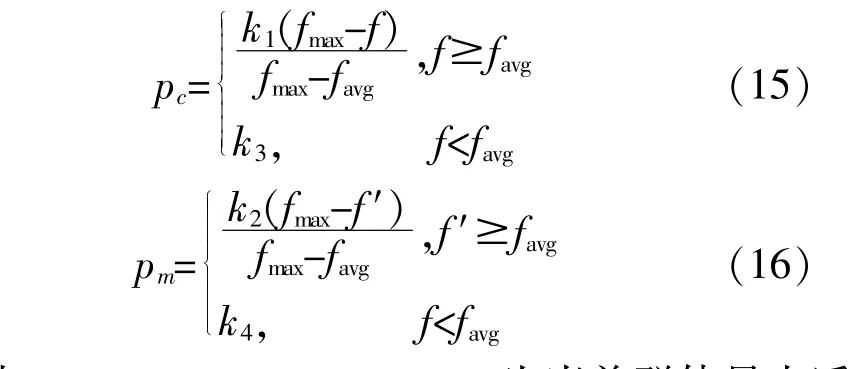
式中：0≤ki≤1，i=1，2，3，4；fmax为当前群体最大适应度；favg为当前群体平均适应度；f为用于交叉两个个体中较大的适应度；f＇为将要变异的个体适应度。

⑤退火过程对新个体的接受。通过上述遗传算法产生的一组新个体，独立随机地选择每个个体两个基因作为扰动点，如果个体适应度增加，则接受新个体，否则按式（16）概率接受新个体。

式中：p（Tk+1）为在Tk+1温度下的接受概率；fk+1，fk分别为新个体、旧个体的适应度值；α为降温系数[14]，[15]。

4 平抑光伏发电出力波动的储能容量优化

储能系统具有动态吸收、适时释放能量的特点，有效弥补了风电、光伏发电间歇性、波动性的不足，改善了间歇式电源输出功率的可控性及电能质量，提高了电能稳定性水平及优化了发电系统的经济性。电储能大致分为机械式储能、电磁储能和化学储能三大类，各种储能装置的技术比较如表2所示。

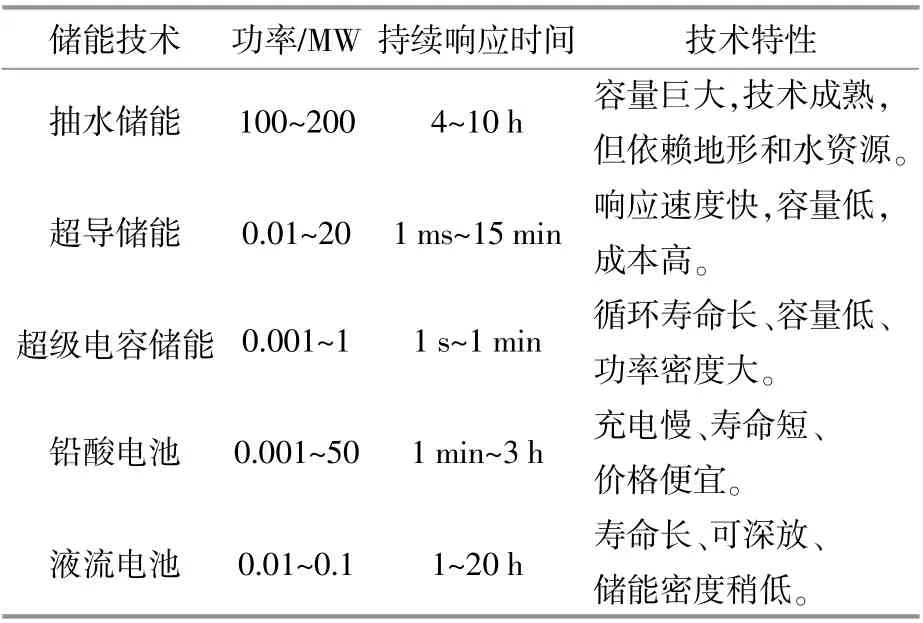
表2 各种储能装置技术比较Table 2 Technical comparison of various energy storage devices

与其他储能方式相比，超级电容储能具有功率密度大、循环寿命长、易检测、环境友好等优点，可用于系统短时间的功率支撑[16]。依据Q/GDW 617—2011《光伏电站接入电网技术规定》，平抑目标为每分钟有功功率变化速率不超过装机容量的10%。

在平抑光伏电站功率波动应用场景下，根据时间跨度为360 d的光伏功率数据，以及储能系统控制策略计算得出的储能系统360 d的充放电功率，计算第j天所需储能容量。

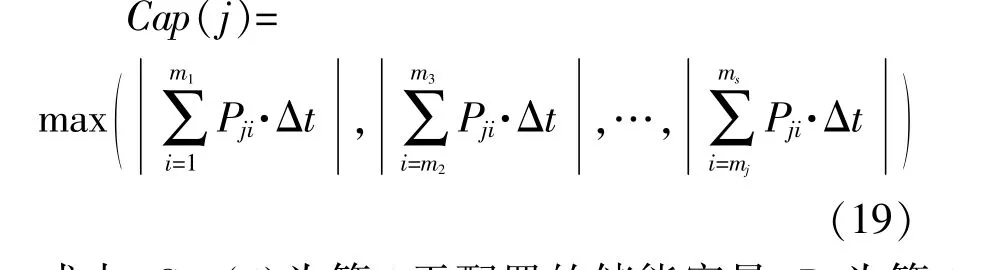
式中：Cap（j）为第j天配置的储能容量；Pji为第j天i时刻的充放功率值；Δt为采样间隔；1～m1，m2～m3，mj～ms为储能不间断充放电的数据采样时刻。

5 算例分析

本文选择IEEE 33节点配电系统为算例，如图3所示，系统信息参考文献[3]。选择某市2020年全年2 MW光伏电站发电历史数据作为分布式光伏发电出力参照，光伏发电出力归一化曲线如图4所示，在33节点标准配电系统开展分布式光伏规划分析。

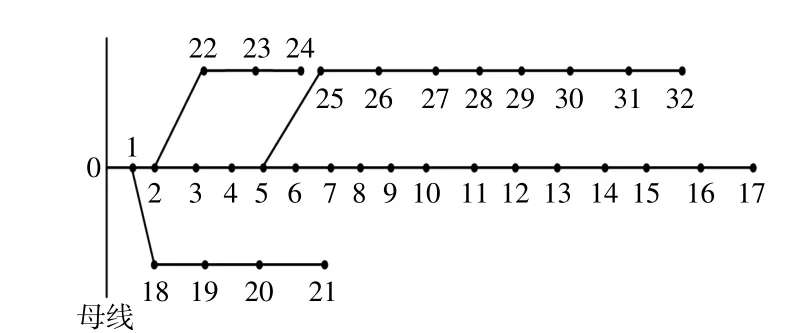
图3 IEEE 33配电系统Fig.3 IEEE 33 power distribution system

图4 光伏发电出力归一化曲线Fig.4 Normalization curve of PV power generation

首先采用DTW距离计算分布式光伏发电功率曲线之间的距离；然后采用K中心点聚类算法对全年光伏发电曲线进行聚类分析；最后采用轮廓系数评估聚类效果，确定最佳聚类簇。光伏发电典型场景模式如图5所示。

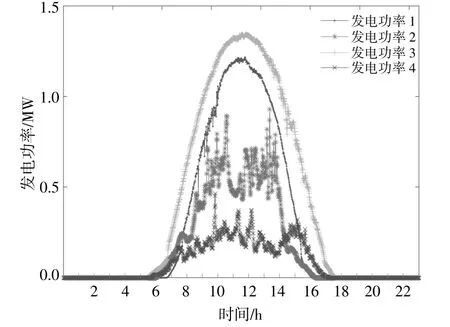
图5 分布式光伏典型聚类场景Fig.5 Typical clustering scenario of distributed power supply

参照居民用户负荷、商业负荷用电规律，以IEEE 33配电系统32个bus节点负荷为24时段平均负荷，生成负荷时序仿真，节点23，24，31为商业负荷，其余为居民用户负荷。各节点24个时刻负荷如图6所示。

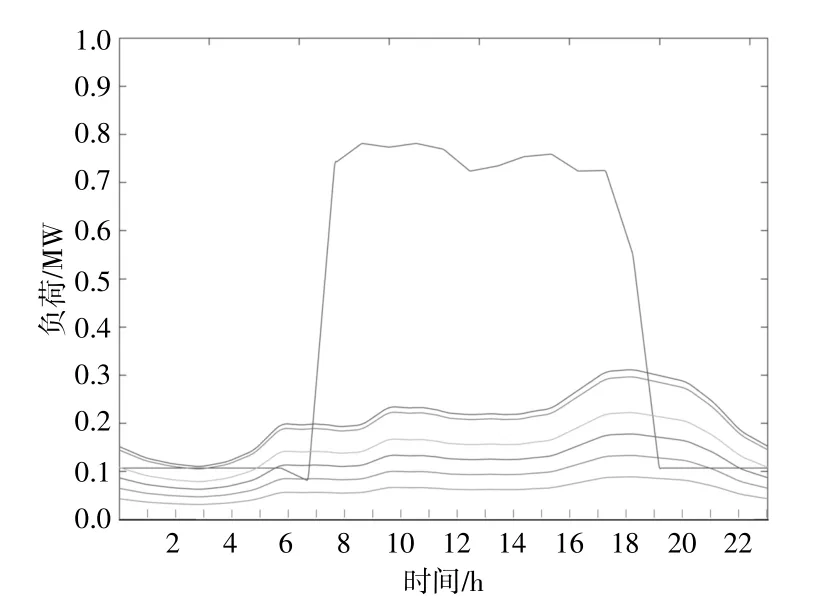
图6 32节点24时段负荷仿真Fig.6 32 node load simulation of 24 hours

IEEE 33节点标准配电网最大负荷为5.5 MW，设置光伏容量渗透率上限为30%，光伏最小单位容量为0.1 MW，32个节点均可作为光伏安装位置，单节点最大光伏容量为0.3 MW。1 MW光伏投资成本为500万元，每年运行维护成本为5万元。光伏发电上网电价为0.045万元/（MW·h），居民电价为0.055万元/（MW·h），商业电价为0.075万元/（MW·h）。光伏发电设备的使用寿命为20 a，使用寿命期内贴现率均为0.05。通过聚类分析得到光伏发电4种典型场景，构建4个联合时序场景，按照各联合时序场景等概率分布，采用简单遗传算法、改进遗传算法分别开展配电网分布式光伏选址定容优化，结果如图7所示。

图7 算法适应度曲线Fig.7 Algorithmic fitness curve

由图7可以看出，改进遗传算法在迭代20次后基本达到最优结果，光伏设备使用寿命期内总的经济效益达到1 090万元。光伏安装容量为1.6 MW，一次投资800万元。光伏安装位置及容量如表3所示。

表3 光伏安装位置及容量Table 3 PV installation position and capacity

为了满足电网对光伏出力稳定性需求，采用超级电容平抑光伏出力波动。光伏发电典型场景1的储能充放电功率如图8所示。

图8 储能设备充放电功率Fig.8 Charging and discharge power of the energy storage equipment

场景1为2 MW光伏设备，储能装置最优配置容量为0.088 7 MW。安装储能前后场景1的光伏出力曲线如图9所示。安装储能装置后，光伏电站每分钟有功功率变化速率不超过装机容量的10%。

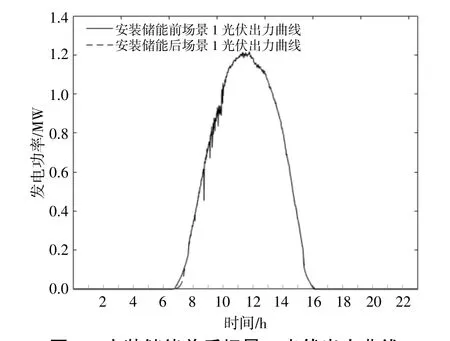
图9 安装储能前后场景1光伏出力曲线Fig.9 PV output curve of scenario 1 before energy storage installation

同理，开展场景2，3，4的储能设备容量优化分析，最佳容量分别为0.073 8，0.081 6，0.063 5 MW。为了满足各种场景容量需求，储能设备最佳容量为0.887 MW。33节点配电网的光伏总安装容量为1.6 MW，各个安装位置共需配置0.071 0 MW的超级电容。

6 结论

光伏电站出力具有很强的波动性，本文采用改进的K中心点聚类算法提取光伏出力典型场景。考虑负荷、光伏出力时序特性，构建光伏、负荷联合时序场景；充分考虑光伏安装运维成本、售电、节能降损效益，以光伏电站经济效益最大化为目标，采用改进遗传模拟退火算法搜寻光伏电站的最优位置和容量。最后，通过超级电容平抑分布式光伏发电出力波动，优化储能装置充放电功率曲线，确定储能位置和容量。该方法实现了光伏电站投资效益最大化，同时也保障了电网安全稳定运行。