立式磨削工艺系统建模方法及仿真研究

薛宝珠，李梦阳

(中国工程物理研究院机械制造工艺研究所，四川绵阳 621900)

0 前言

由于磨削加工获得的工件精度比其他加工方式高，磨削加工常作为加工的最后一道工序。高精度磨削技术在精密仪器、超精密机床、航空航天等行业领域具有广泛用途。套类零件是超精密机床中主轴以及转台的关键零件，是保证超精密机床加工精度的关键要素。由于立式磨削可以一次装夹完成内孔、外圆以及端面的多结构要素加工，相比于其他磨削方式误差累积小，有益于改善套类零件加工效率和加工精度[1-4]。

随着对磨削精度的要求不断提高，通过建立模型来模拟磨削过程，从而实现对磨削结果的预测、工艺参数的优化和磨削过程的控制，成为提高磨削效率和精度的重要手段[5-11]。本文作者通过对立式磨削工艺系统进行静力学分析，建立立式磨削圆度误差的数学模型，并借此研究各因素对磨削精度的影响规律。

1 立式磨削工艺系统模型

图1所示为典型立式磨削工艺系统的结构[1]，主要包括转台、工件、砂轮、主轴和机床本体等零部件。

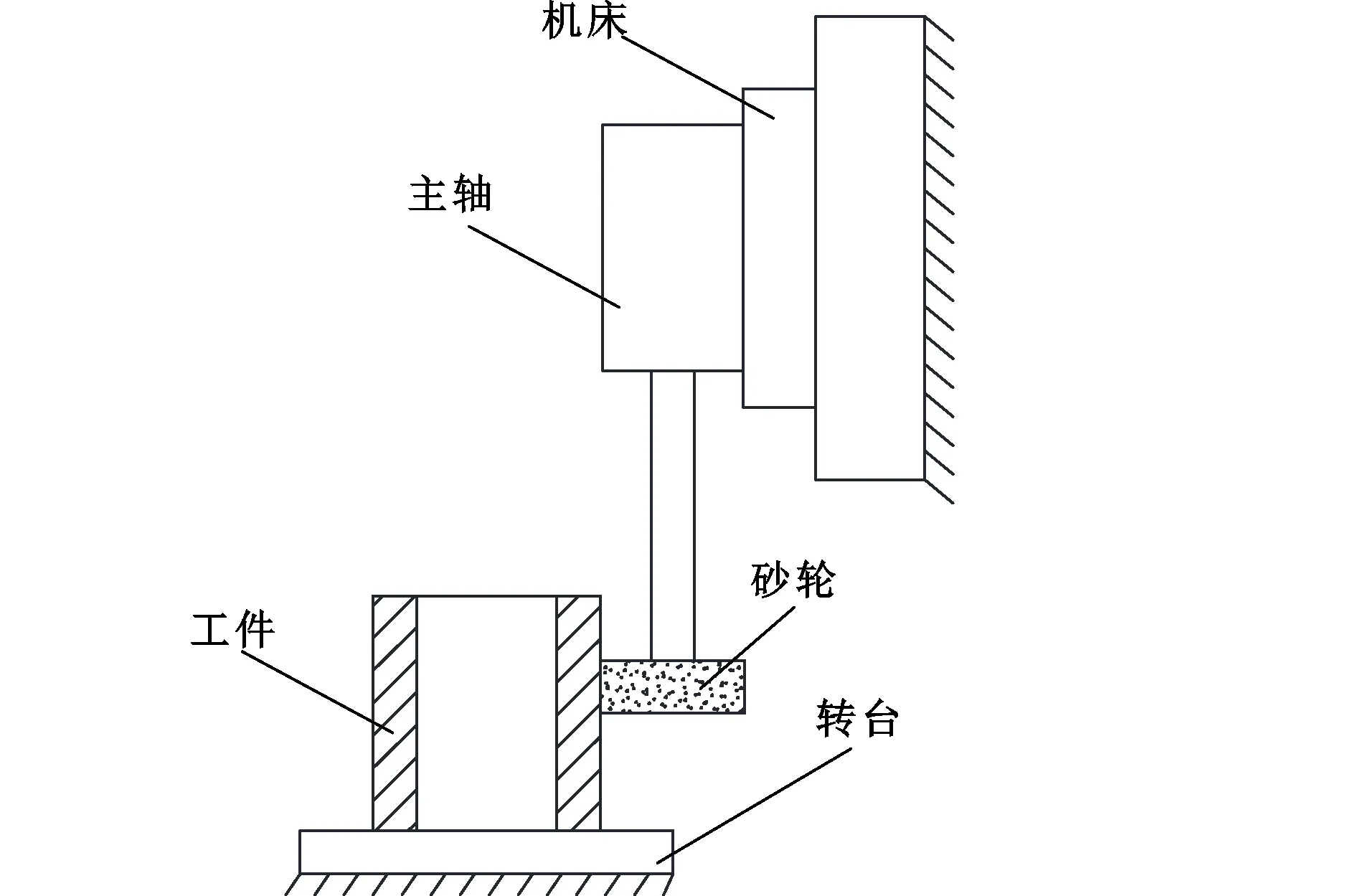
图1 立式磨削工艺系统结构示意

立式磨削工艺系统十分复杂，建模需要考虑工件系统、砂轮系统、液体静压支承、直线电机、刚性接合面、砂轮杆柔性等。为减少系统复杂性，重点探索工件系统和砂轮系统对整体系统的影响，作如下假设：

(1)相比于转台、工件、砂轮、主轴之间的接触刚度，机床本体的刚度大，因此将机床本体视为刚体；

(2)CBN砂轮硬度大，短时间磨削磨损小，因此忽略砂轮磨损；

(3)高精度磨削发热量小，同时采用切削液冷却，故工件温度变化小；温度场沿周向均匀变化，对圆度影响很小，因此不考虑磨削过程中热效应对圆度的影响;

(4)此例中工件线速度小，磨削力小；采用液体静压支承，有隔振效果，为便于研究，假设系统为准静态。

图2所示为立式磨削工艺系统的简化图，其中：ez为转台回转误差，es为主轴回转误差；转台和工件之间作用简化为弹簧支承，刚度为kg，工件中心位移为xg；主轴和砂轮之间作用简化为弹簧支承，刚度为ks，砂轮中心位移为xs；砂轮和工件之间的接触变形用接触刚度ka表征；u为主轴的瞬时进给量。

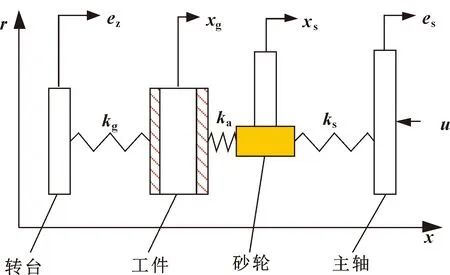
图2 立式磨削工艺系统简化模型

定义磨削瞬时深度为ap，对应的磨削力为Fn，有如下关系：

(1)

定义kw为磨削刚度，则有：

(2)

式中：uch为比切削形成能；b为磨削宽度；vw为工件线速度；vg为砂轮线速度；λ为法向磨削力和切向磨削力的比值。

在此力作用下，砂轮与工件的接触变形为

(3)

工件与砂轮位移、磨削深度与接触变形满足几何关系：

ap=xg-xs+u-δ+eg

(4)

式中：eg为当前磨削点的工件轮廓误差。当前磨削点的工件轮廓误差是上一轮磨削完成后原始轮廓减去上一轮的磨削去除量：

eg(n)=eg(n-1)-ap

(5)

分别以工件和砂轮为分析对象，可以得到静力学平衡方程：

kg(ez-xg)-Fn=0

(6)

Fn-ks(xs-es)=0

(7)

整理式(6)(7)可得：

(8)

(9)

综合式(2)—(9)，有:

ap=(ez-es+u+eg)/(1+kw/ka+kw/kg+kw/ks)

(10)

工件的初始轮廓误差eg0、转台回转误差ez及主轴回转误差es为可测量值，为仿真计算方便，采用傅里叶级数对上述误差进行模拟：

(11)

2 仿真算例和试验验证

磨削加工对材料的去除为缓变过程，工件的初始轮廓误差eg0、转台回转误差ez及主轴回转误差es中的高频成分对最终加工形貌的影响不显著，因此仅取误差的前4阶频率成分作为分析条件，即：

(12)

(13)

(14)

为验证仿真模型的正确性，进行仿真算例计算及试验验证。表1、2所示为仿真和试验的工件参数和相关磨削工艺参数。

表1 材料为38CrMoAlA工件参数

按照表1和表2的参数磨削后，仿真计算得到的圆度误差为0.62 μm。图3所示为磨削后的圆度轮廓。可以明显看出：磨削之后的工件仍然存在波浪形的轮廓，但是这种波浪轮廓对圆度误差没有明显的影响。

表2 相关磨削工艺参数

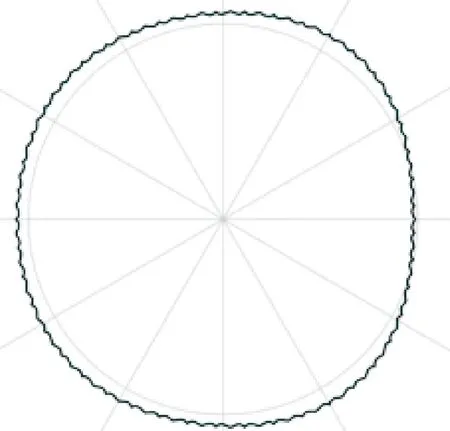
图3 磨削后的圆度

为进一步验证模型的正确性，按照前文的磨削参数，在数控立式磨床上进行了磨削工艺试验，如图4所示。工件磨削后借助Tayler Hobson的圆度仪对圆度误差进行评定，结果表明：磨削后圆度误差为0.6 μm，该值与模型计算结果0.62 μm相比差别很小。由此，证明了前文所述的模型是正确的，表明了利用此模型研究磨削误差影响规律的可行性。

图4 轴套磨削加工

3 圆度误差影响因素分析

对不同磨削工艺参数下的磨削加工进行仿真计算，比较各参数对磨削加工圆度误差的影响规律。

3.1 转速比对加工误差的影响

相比于单独研究砂轮和工件各自的转速，研究砂轮和工件的转速比对工件表面的圆度误差的影响规律对工程实践的指导意义更加明确。

图5所示为保持工件转速在20 r/min，通过改变砂轮的转速改变转速比，且转速比始终为整数时对圆度误差的影响规律。可知：随着转速比的增大，工件的加工圆度误差逐渐减小，且刚开始减小得很快，当转速比增大到一定程度时，减小趋势开始趋缓。

图5只给出了转速比为整数时的影响规律，而实际上，相比于研究转速比的整数部分，研究其小数部分对圆度误差的影响也有重要意义。

图5 砂轮和工件转速比对圆度误差的影响 图6 波偏对圆度误差的影响

转速比的小数部分可以用波偏Δ来表示。砂轮和工件的转速比减去不超过它的最大正整数，得到的余数可以定义为波偏。它表示第N转的磨削波形轮廓相对于第N-1转轮廓的相位偏移。如果转速比是整数，那么波偏为0，这会造成最大的圆度误差。非整数转速比导致的波偏效应可以减小圆度误差，尤其在光磨阶段。

图6所示为不同波偏对圆度误差的影响规律。可以看出：当波偏Δ为0，即转速比为整数时，圆度误差最大，为2.01 μm，其次为波偏Δ为0.5时，圆度误差为1.02 μm，而波偏Δ为0.1或0.9时，圆度误差最小，为0.33 μm。

图7所示不同波偏下加工得到的圆度轮廓，可以直观地表现出波偏对加工轮廓的影响。在图7中，波偏Δ为0时的外轮廓最为陡峭，且轮廓的频率最低，而波偏Δ为0.1时外轮廓最为平缓，且频率最大。

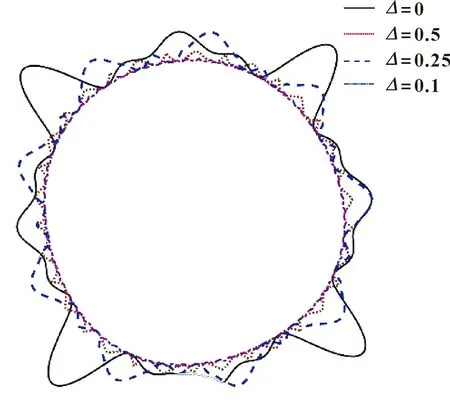
图7 不同波偏影响下的圆度轮廓

3.2 工件初始圆度的相位对加工误差的影响

由式(12)可知，影响工件初始圆度轮廓的因素主要为各频率成分的幅值和相位，由于高频成分对圆度的影响很小，故分析前4阶频率的影响更有意义，即：

(15)

(16)

在加工时间足够长的情况下，工件初始圆度误差的幅值对最终加工误差的影响不大，因此主要分析相位对加工精度的影响。

取不同的相位矩阵：

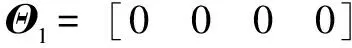
得到的磨削加工轮廓如图8所示。为使3条曲线易于比较，每条曲线的偏移系数不同。可以发现：不同相位矩阵Θ1、Θ2、Θ3下，磨削得到的轮廓形状相同，且Θ2、Θ3的轮廓相比对Θ1的轮廓，沿着中心点旋转了一定角度。但是3个轮廓的圆度误差都为0.53 μm。因此，相位的大小对最终的加工圆度不会产生影响。

图8 不同相位工件初始圆度下加工得到的圆度轮廓

3.3 磨削时间对加工误差的影响

假设将工件磨削到极限圆度所用的时间为Th，为探究磨削过程中不同阶段的圆度轮廓演变情况，分别计算出在Th/5、2Th/5、3Th/5和Th时刻的圆度轮廓，如图9所示。在磨削开始阶段(0～2Th/5)，砂轮不断加工外圆，圆度误差下降很快；经历一段时间之后(2Th/5～3Th/5)，圆度误差随着磨削过程缓慢降低；在磨削接近完成时(3Th/5)，此时继续磨削，磨削误差随时间的变化极小。

图9 不同磨削时间的圆度轮廓

3.4 主轴旋转误差对加工误差的影响

主轴作为立式磨削工艺系统的重要功能部件，其回转精度将直接影响砂轮的回转精度，对保证工件的加工精度起着重要的作用。因此，重点分析主轴回转误差对工件加工圆度误差的影响规律。

图10所示为不同主轴回转误差幅值下加工得到的工件圆度误差。可知：随着主轴回转精度的降低，工件的加工精度也逐渐降低。

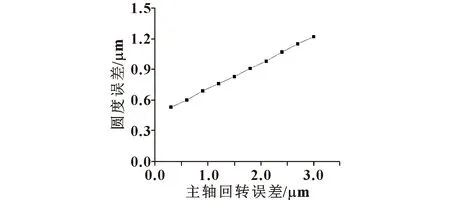
图10 主轴回转误差对圆度的影响

为对比分析主轴回转误差中不同阶次误差的影响规律，仿真计算不同回转误差幅值及最高阶次下的加工精度，结果如图11所示。可以看出：3阶误差导致的圆度误差最大，2阶最小；各阶误差造成的加工精度差较小，且差值随着主轴回转误差的增大而增大。

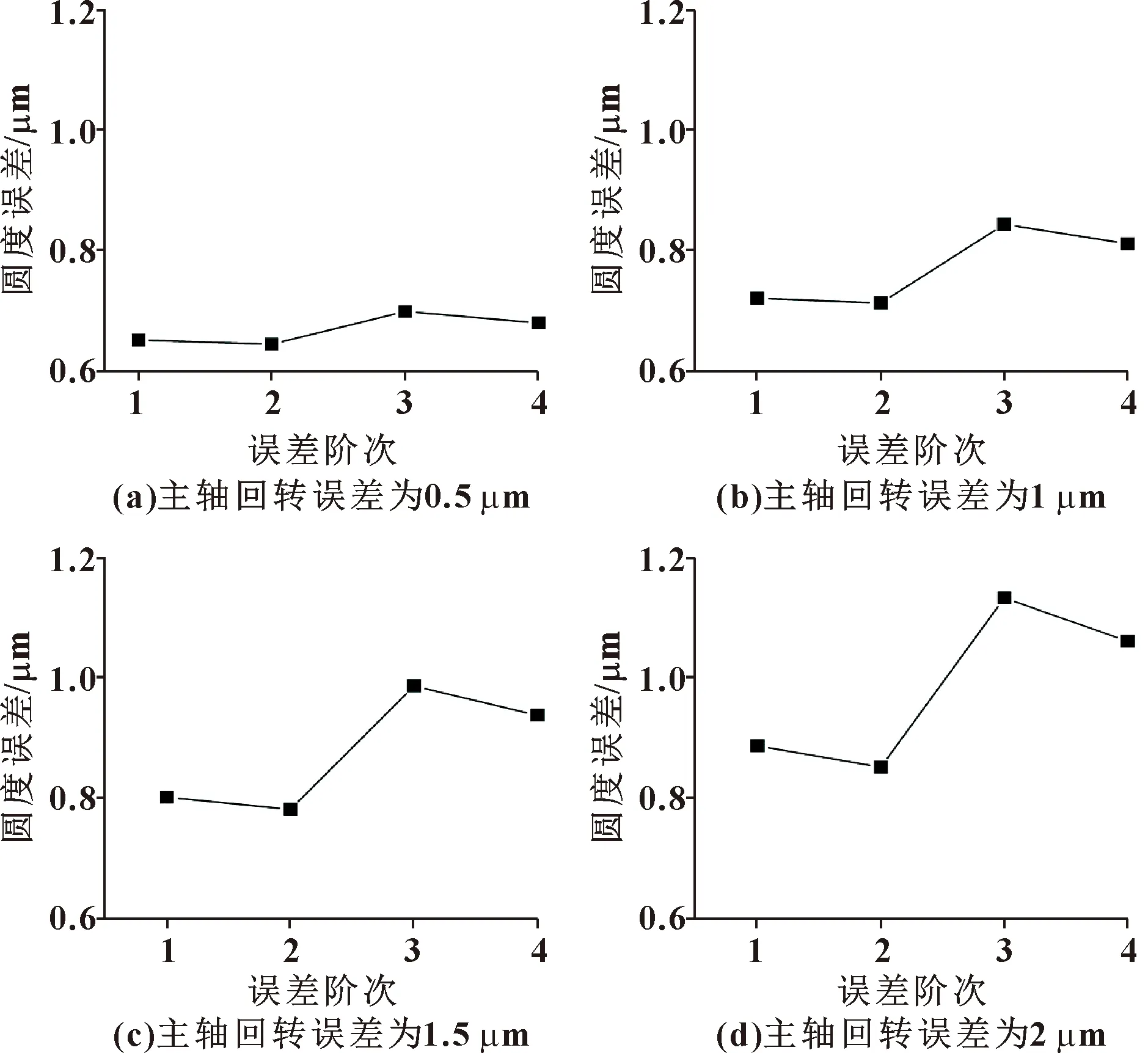
图11 不同误差幅值及阶次对圆度的影响

5 结论

(1)采用静力学方法建立了立式磨削工艺系统的误差分析模型，模型计算结果与试验基本一致。该模型能用来预测磨削行为和磨削误差，进而为磨削参数优化提供参考。

(2)分析了转速比、工件初始圆度误差相位、磨削时间和主轴回转误差对磨削精度的影响规律。当转速比为整数时，磨削精度随着转速比的增大而提高；当转速比不是整数时，变化情况更加复杂。工件初始圆度误差的相位对最终的加工圆度不会产生影响。随着磨削的进行，工件圆度误差开始降低得很快，随后降低趋势逐渐变缓。在主轴误差的组成频率中，3阶误差导致的圆度误差最大，2阶最小。