基于数控指令修正的数控内圆磨床几何误差补偿

范晋伟，秦池，潘日

(北京工业大学机械工程与应用电子技术学院，北京 100124)

0 前言

随着机械制造业的不断发展，各种数控机床、磨床、加工中心发展得越来越快，这些技术的发展水平也代表着一个国家生产制造水平的高低。数控磨床作为多数零件加工的最后一道工序所用的设备，其加工精度起到至关重要的作用。但是，在实际加工过程中，由于一些外部环境、机床振动、刀具磨损及热源的影响，使得生产的零件总会存在加工误差，所以减少或者消除加工误差非常有必要。影响机床的误差源多种多样，如几何误差、热误差、伺服系统误差等，而每种误差都会对机床的加工精度产生一定的影响，如何通过减小误差影响提高加工精度成为至关重要的研究问题。

空间运动误差的建模方法前期主要有三角函数法[1-2]、矢量描述法[3]等，后来经过学者们的不断研究，出现了机构学理论[4]、多体系统理论[5-8]、螺旋理论[9-10]等建模方法。多体系统是多个刚体或者柔体通过某种连接方式而形成的复杂机械系统，同时也是对复杂机械系统的完整抽象和有效描述[11]。它通过对机床整体的运动结构进行抽象化处理，简化其结构的复杂性，能够借助计算机快速建模，具有良好的通用性以及系统性，所以非常适用于误差建模[12]。OKAFOR和ERTEKIN[13]利用齐次坐标变换原理并且忽略高阶误差项，建立了多轴机床的空间误差模型。CHEN等[14]以多体系统理论为基础，推导出五轴数控机床的运动误差公式。WU等[15]通过齐次坐标变换原理以及多体系统理论，建立了非正交五轴数控机床的空间运动误差公式。

现阶段的研究多为五轴机床及加工中心的几何误差分析，关于磨床的研究相对较少，且磨床的空间运动误差建模没有统一步骤，存在模型精度不足等问题。为更加全面且精准地分析磨床的几何误差，提高加工精度，本文作者基于多体系统理论建立数控内圆磨床的空间运动误差模型。通过研究数控指令修改算法进行误差补偿，得到精密加工的数控指令，并对加工阶梯轴试件进行仿真验证，得出补偿前后的数控指令，分别选取5个补偿点，对比补偿前后到理想位置的空间距离。

1 基于多体理论的空间运动误差建模

1.1 机床结构简述

图1所示为文中选用的数控精密内圆磨床结构模型。它是由两个移动轴、两个旋转轴以及机身、刀具等构成，其中：x、z轴为移动轴；A、B轴为旋转轴；刀具通过B轴(刀具转台)进行换刀，B轴借助x轴进行x方向的移动；z轴带动x轴、B轴以及刀具等进行z方向的移动。

图1 数控精密内圆磨床结构简图

1.2 数控精密内圆磨床的拓扑结构及低序体阵列

基于多体系统理论，可以将该内圆磨床简化为具有2个分支的多体系统，其中一个是床身-刀具分支，主要由机身、z轴导轨、x轴滑座、B轴转台、刀具组成；另一个是床身-工件分支，主要由机身、导轨、工件主轴(A轴)、工件组成。依据多体系统理论中的命名规则，对磨床主要零部件进行序号标定，其中：机身为1体；z向滑台为2体；x轴为3体；刀具转台为4体；刀具为5体；工件主轴为6体；工件为7体，并在点o1、o2、o3分别建立相应坐标系，得到的磨床拓扑结构如图2所示。

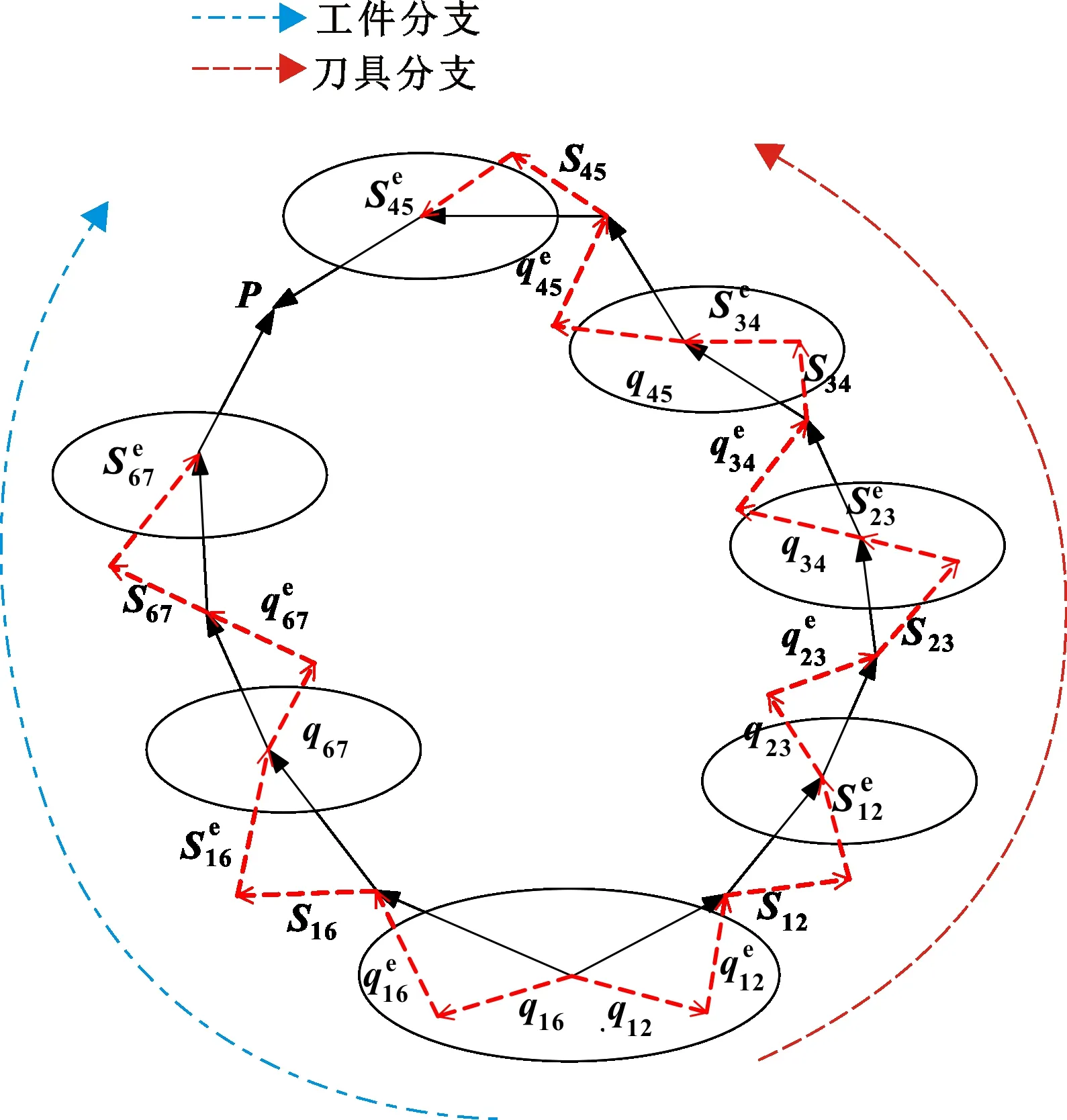
图2 磨床拓扑结构

由磨床的拓扑结构图，可以得到如表1所示的低序体阵列。

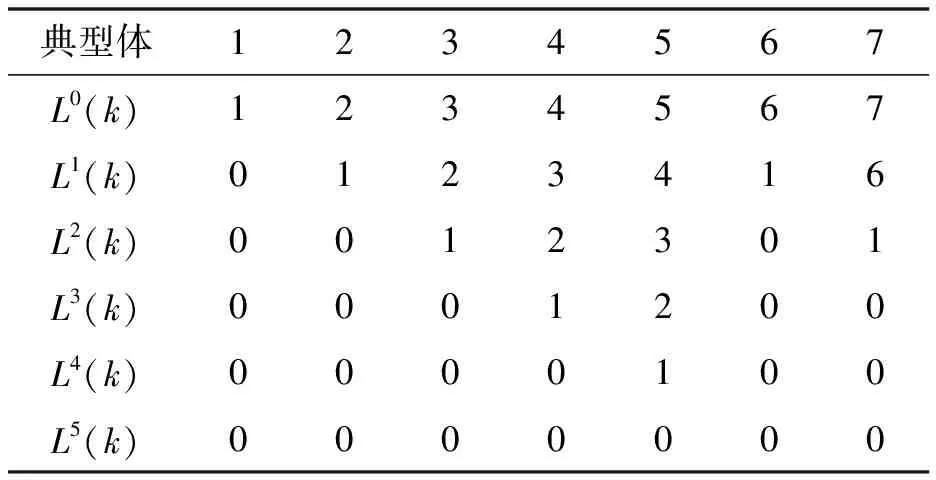
表1 低序体阵列

1.3 数控精密内圆磨床几何误差分析

任意物体在空间运动时有6个自由度，则会产生6项几何误差[16]，其中包括3项线位移误差：定位误差以及2个直线度误差；3项角位移误差：倾斜误差、偏摆误差以及俯仰误差。直线轴以x轴为例，6项误差分别为x向的定位误差δx(x)、y向的直线度误差δy(x)、z向的直线度误差δz(x)、绕x轴的偏摆误差εx(x)、绕y轴的俯仰误差εy(x)以及绕z轴的滚转误差εz(x)；旋转轴以C轴为例，6项误差分别为径向跳动误差δx(c)和δy(c)、轴向跳动误差δz(c)、倾斜误差εx(c)和εy(c)、定位误差εz(c)，x、C轴几何误差参数如图3、4所示。轴与轴之间还存在相对位姿误差，主要为各轴之间的垂直度误差。综上所述，该数控精密内圆磨床的几何误差参数共有29项，具体如表2所示。

图3 x轴几何误差参数示意

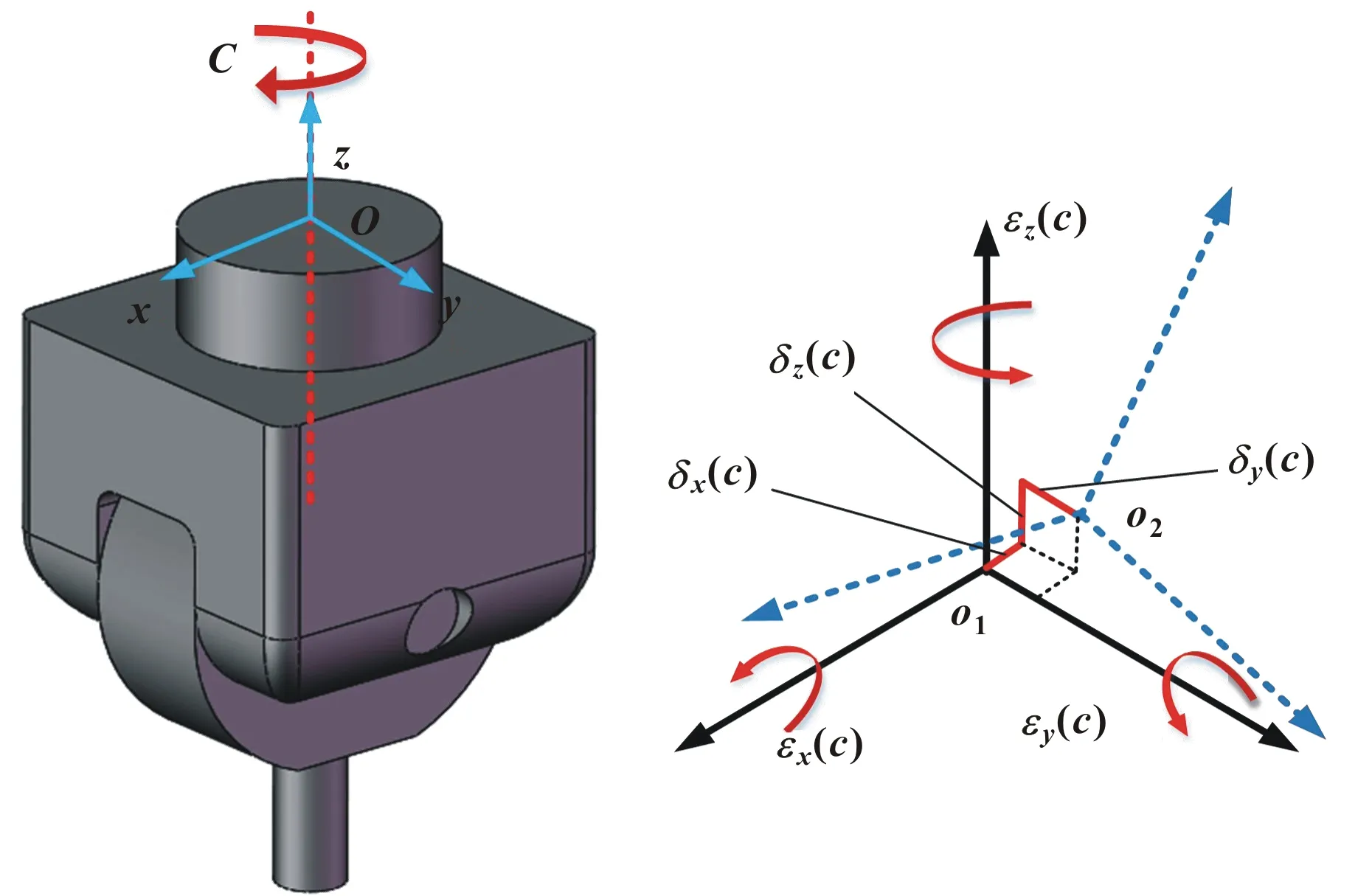
图4 C轴几何误差参数示意

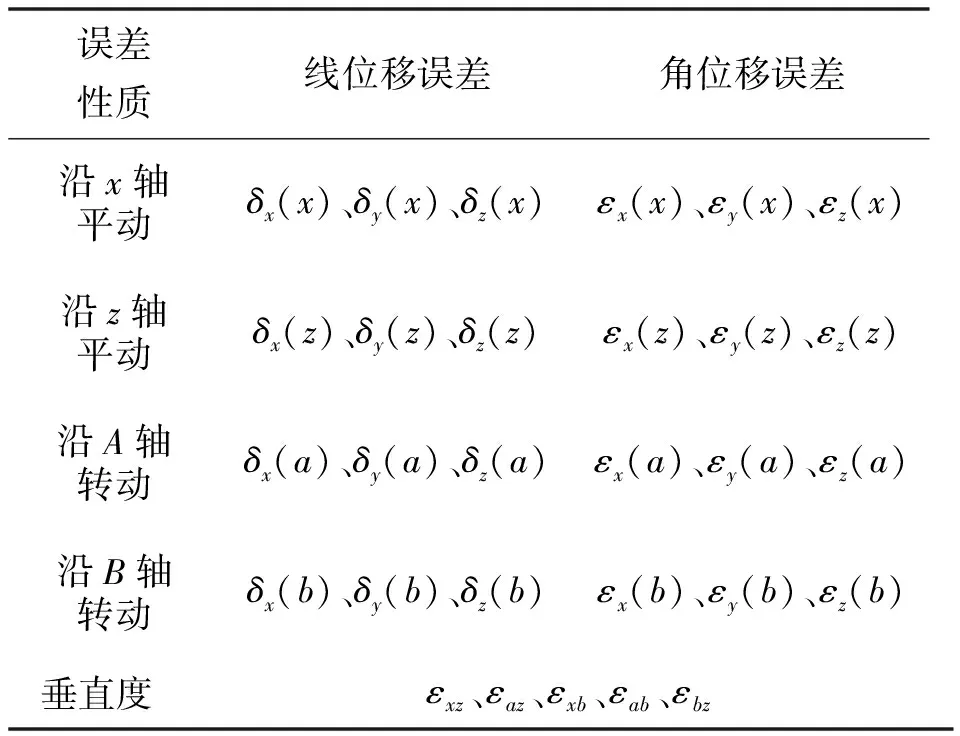
表2 数控精密内圆复合磨床几何误差参数

1.4 数控精密内圆磨床的空间运动误差模型

根据低序体阵列表以及相对运动关系，基于齐次坐标变换原理，可得到数控内圆磨床相邻体之间的理想静止齐次变换矩阵及实际静止齐次坐标变换矩阵、理想运动齐次变换矩阵及实际运动齐次坐标变换矩阵[17]，分别如表3和表4所示。

表3 理想静止及实际静止齐次坐标变换矩阵

表4 理想运动及实际运动齐次坐标变换矩阵

设被加工点为P，则点P分别按照机身-刀具分支、机身-工件分支表示在机床坐标系中，位置分别记为Pt0、Pw0,基于多体系统理论，可以得其表达式为

Pt0=S12，pS12，peS12，sS12，seS23，pS23，pe·

S23，sS23，seS34，pS34，peS34，sS34，seS45,pS45,peS45,sS45，sert

(1)

Pw0=S16，pS16，peS16，sS16，seS67，pS67，peS67，sS67，serw

(2)

其中：rt为点P在刀具坐标系中的位置矩阵；rw为点P在工件坐标系中的位置矩阵。在实际加工中，为实现精密加工，必须满足刀具成形点与工件成形点重合，即必须满足以下条件：

Pt0=Pw0

(3)

由公式(3)可以得到实际情况下被加工点P在工件坐标系中的位置：

rw，actual=

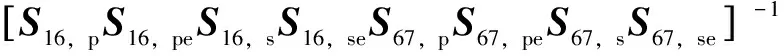
S12,pS12,peS12,sS12,seS23,pS23,peS23,sS23,seS34,p·

S34,peS34,sS34,seS45,pS45,peS45,sS45,sert

(4)

将公式(4)中的误差矩阵省略，可以得到理想情况下待加工点P在工件坐标系中的位置：

rw,ideal=(S16,pS16,sS67,pS67,s)-1·

S12,pS12,peS12,sS23,pS23,sS34,pS34,sS45,pS45,srt

(5)

则该磨床的空间运动误差模型为

E={Ex,Ey,Ez}=rw,actual-rw,ideal

(6)

其中：Ex、Ey、Ez分别为空间误差在x、y、z方向的误差分量，将公式(4)(5)及静止矩阵、运动矩阵、误差矩阵代入公式(6)，经过MATLAB软件求解，并且忽略高阶无穷小量，最终可求解出数控精密内圆磨床的空间运动误差模型。

将检测的误差数据代入所建立的空间运动误差模型中，即可计算出数据点的空间误差，通过对数控指令进行修正，能提高机床的加工精度，且修正量即为数据点的空间误差值。下面以直线插补运动为例进行数控指令修正算法研究。

2 直线插补运动数控指令修正

2.1 确定补偿点

补偿点数的确定，会对加工指令的精度产生重要影响：如果选择点数过多，会导致加工指令数目巨大；点数过少，则会导致精度低等问题[18]。对于补偿点数的选取，一般有两种方法：垂直分割法、水平分割法[19]。水平分割法能够较好地提高补偿点处的加工精度，且相邻补偿点之间的精度也能得到有效控制。相对于垂直分割法，水平分割法确定的补偿点数少，生成的数控指令容量小，故选用水平分割法进行补偿点确定。图5所示为水平分割法示意图。

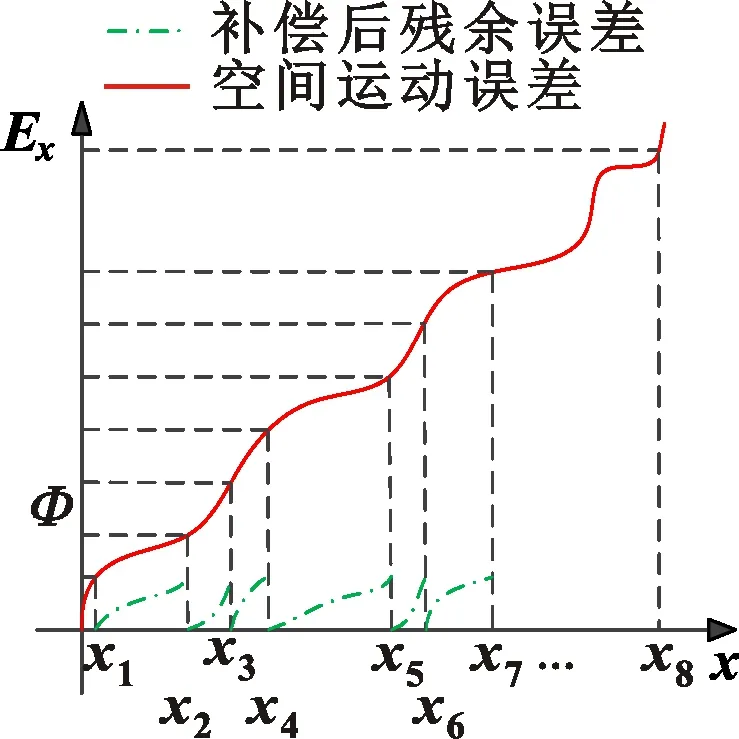
图5 水平分割法

2.2 直线插补运动数控指令修正

对于直线运动的补偿，应从直线起点Pa开始，根据直线方程表达式，得到该点的坐标，并基于得到的空间运动误差模型，计算该点在x、y、z方向的误差Δx(Pa)、Δy(Pa)、Δz(Pa)，并分别判断三者的绝对值，若起点Pa数据满足公式(7)，则该点不需要补偿，沿直线继续进行下一点判断；若三者中任意一项或者几项超过控制精度Φ，则起点必须进行补偿;直线中其他点Pn则按照公式(8)进行计算，其中Δx(Pn)、Δy(Pn)、Δz(Pn)分别为点Pn处的误差，Δx(Pn-1)、Δy(Pn-1)、Δz(Pn-1)为前一个补偿点处的误差，若符合公式(8)，则证明该点不需要补偿，反之该点为补偿点。

(7)

(8)

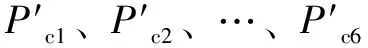
图6 补偿前直线运动轨迹

图7 补偿后直线运动轨迹

3 仿真验证

基于上述研究的误差补偿方法，以内圆磨床常用加工零件阶梯轴进行仿真验证。试件三维模型如图8所示，表5所示为试件具体结构参数，加工刀具直径为φ40 mm。对直线运动数控指令的修正算法进行研究，并结合建立的空间运动误差模型，进行试件加工仿真验证。

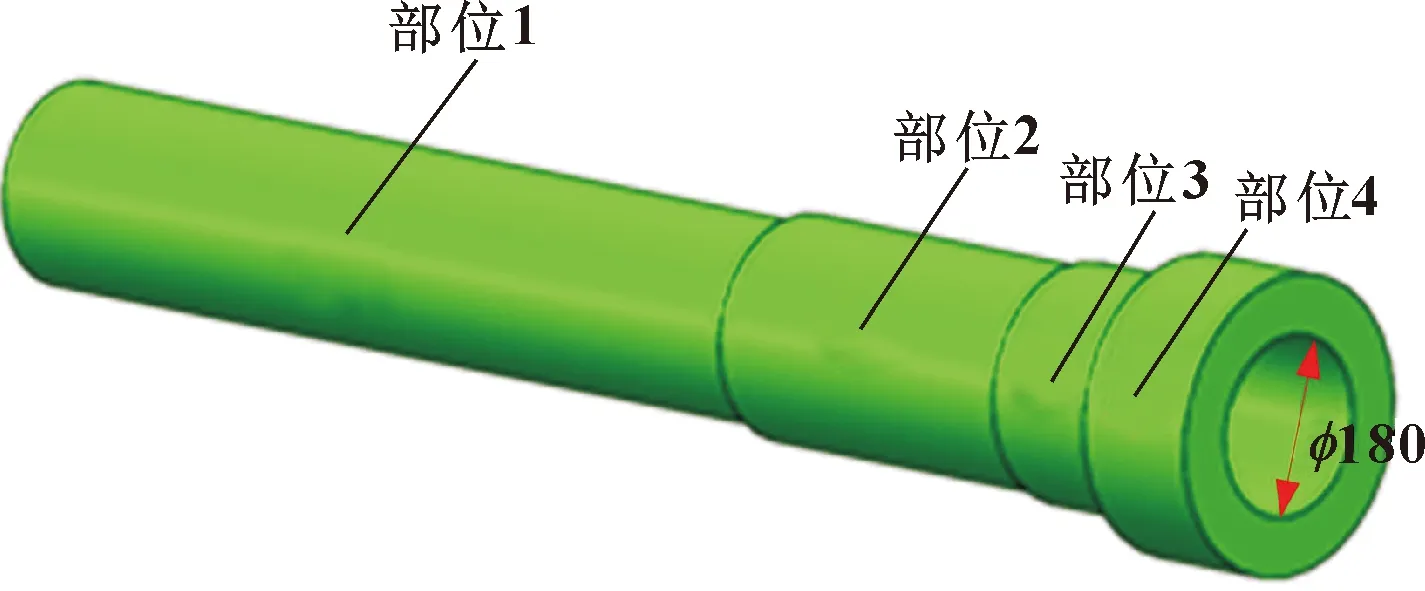
图8 试件三维模型

表5 阶梯轴结构参数 单位：mm

由于加工中涉及到29项几何误差，故首先设定几何误差参数值，并结合空间运动误差模型，算出补偿点处x、y、z方向的误差；其次，对每个补偿点的误差进行判断，对其进行补偿。将未补偿的数控指令导入软件中，如表6所示，并进行走刀模拟；对补偿点处误差进行补偿，得到如表7所示的补偿后对应的数控加工指令，并生成补偿前后的走刀轨迹，如图9所示。

表6 补偿前数控指令 单位:mm

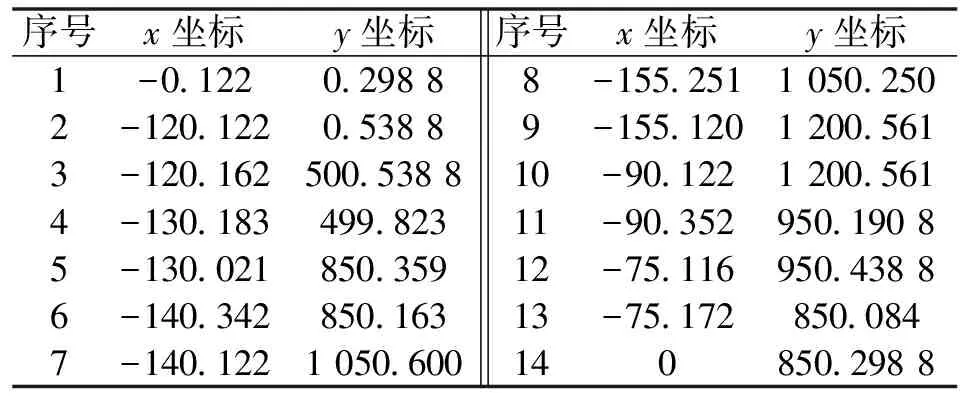
表7 补偿后数控指令 单位:mm

图9 补偿前后走刀轨迹

分别对比图9中由上向下的5个画圈点补偿前后的数据，如表8所示。

表8 补偿前后数据 单位：mm

由表8可知：5个数据点补偿前后距离理想位置的空间距离分别由0.616、0.607、0.614、0.295、0.376 cm变为0.354、0.398、0.376、0.188、0.255 cm，分别减小了42.5%、34.4%、38.6%、36.3%、32.1%。

4 结论

以数控精密内圆磨床为研究对象，首先基于多体系统理论，建立磨床的空间运动误差模型，基于此模型，可以求解加工路径中任意点的空间误差；其次，通过对比垂直分割法与水平分割法的优缺点，得出水平分割法能够有效保证相邻补偿点之间的精度，故选择水平分割法确定补偿点的数量；以直线运动轨迹为例，进行数控指令修改，得出补偿前后的直线轨迹；对阶梯轴试件进行加工仿真验证，得出补偿前后的数控指令，并选取5个加工点，对比补偿前后的空间误差。结果表明：5个加工点的误差都得到有效提高，证明了所提方法的有效性。