基于BP模糊神经网络PID控制的牵引绞车张力控制研究

朱鹏程，张晴，张文华，舒欣，杨冰华

(1.江苏科技大学机械工程学院，江苏镇江 212003；2.中国特种飞行器研究所，湖北荆门 448035)

0 前言

海洋绞车作为深海装备的一种，承担着海底设备的安装、海洋管道的铺设、水下设备的拖拽等功能[1-3]。现今，由于终端设备对收放精度的要求提高，海洋绞车从传统的牵引及储缆功能为一体的单卷筒绞车进而衍生出了储缆功能和牵引功能分离形式的绞车[4]。文中主要针对储缆及牵引分离形式的绞车中的牵引绞车进行张力控制的研究。

由于海浪、洋流、大风等恶劣环境的影响，牵引绞车所在的母船会产生纵摇、横摇、升沉运动等现象[5-7]，导致牵引绞车在这种情况下进行收放时缆绳上挂载的设备会随船身产生晃动，造成缆绳损坏，甚至是设备丢失，其中，母船的升沉运动对缆绳的影响最大。因此针对上述情况，人们开发出了主动升沉补偿系统(AHC)、混合主动-被动升沉补偿系统(HAHC)以及被动升沉补偿系统(PHC)[8-10]。其中，AHC补偿系统虽然结构及控制算法十分复杂，但因其补偿效率可达95%[11]，所以被大量应用在深海设备中。并且为了获得更高的补偿精度，现在的学者对主动补偿系统的结构及控制算法进行了大量研究。例如：RICHTER等[12]提出了一种依赖基于莱文森递推最小二乘算法进行运动预测的综合主动升沉补偿系统。MOSLÅTT等[13]对一种使用半二次控制(SSC)方法的新型主动升沉补偿式海洋起重机控制器进行了实验验证。YAN等[14]提出了一种基于反步法的自适应鲁棒积分滑模控制器来实现重型深海拖拽系统升沉补偿器的恒张力控制。吴汪洋等[15]在 MATLAB/Simulink 软件平台上建立广义预测控制+极短期预报相结合的主动升沉补偿系统时延实时控制模型。从上述来看，绝大部分对升沉补偿的研究主要针对单卷筒结构液压绞车以及位移补偿的研究，对于基于船基的电驱动牵引绞车张力控制的研究很少。因此，本文作者针对升沉作用下缆绳张力不断震荡的问题，分别建立了基于传统PID控制、模糊PID控制及BP模糊神经网络PID控制的牵引绞车张力控制器进行缆绳张力补偿。通过仿真比较，基于BP模糊神经网络PID控制的张力控制系统具有更快的反应速度以及更好的稳定性。

1 牵引绞车系统动力学分析

1.1 牵引张力控制系统组成及工作原理

文中牵引绞车张力控制系统组成如图1所示，包括缆绳张力传感器、牵引绞车控制器、牵引绞车。牵引绞车张力控制的工作原理为：通过设置在滑轮上的缆绳张力传感器测量负载至牵引绞车入绳端的缆绳张力值；将此值传入牵引绞车控制器，通过控制器驱动牵引绞车电机进行力矩输出，使得负载到牵引绞车入绳端的缆绳保持合外力为零，最终缆绳保持合适的张紧状态。

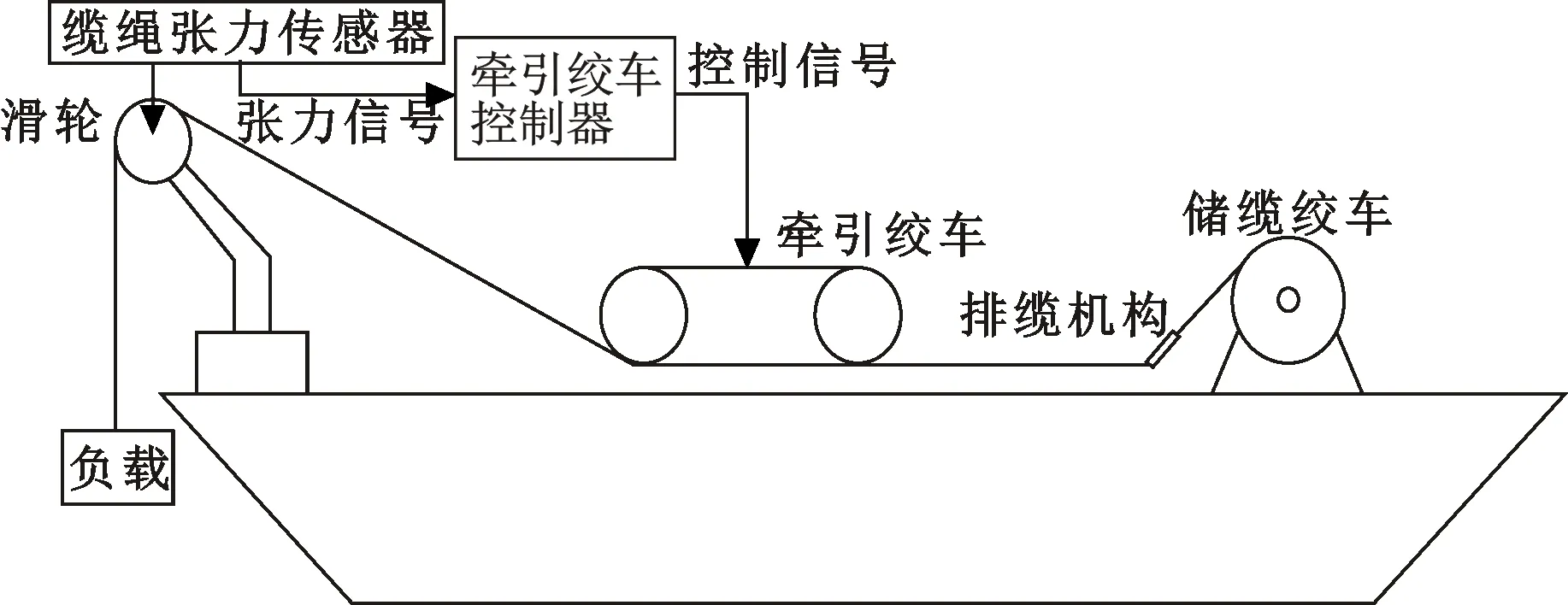
图1 牵引绞车控制系统组成示意

1.2 缆绳张力计算

牵引绞车在下放时缆绳张力的计算分为入水前、入水时以及入水后3个阶段[16]。在入水前，缆绳此时的张力为负载的重力与母船升沉位移所产生的附加张力之和；与入水前相比，不同的是入水时缆绳张力还受到波浪力、海水浮力以及入水时的母船升沉位移所产生的附加张力的影响。而入水后与入水前相比，由于负载整个没入水中，所以可以忽略海水的波浪力的作用。因此，为了知道缆绳的张力需要知道母船的升沉位移、负载所受的浮力、波浪力、负载入水前及入水时相对于地面坐标系的加速度。

将母船在随机海浪下的运动看作升沉运动，母船升沉位移由波高以及船体的类型结构、尺寸等因素决定。文中将母船的运动看作简谐运动。因此，不规则波下母船的升沉位移可以看作由不同周期、波高、初相位的余弦波叠加而成，则其运动方程为

(1)

式中：w为母船升沉位移；Hi为波高；μ为升沉位移与波高的比值；Ti为周期；φi为初始相位。

对式(1)的t求导得到母船的升沉速度v：

(2)

对式(2)的t求导得到母船的升沉加速度a：

(3)

负载所受波浪力的计算前提是需要知道负载入水时的速度即不规则波下水质点的垂直速度、负载下放速度及升沉运动速度。而水质点的垂直速度是根据波浪理论得到。依据当前牵引绞车的收放环境选择微幅波理论来计算水质点的垂直速度。微幅波理论的公式为

(4)

式中：k为波数；L为波长；h为水深；σ为波浪角频率。

将式(4)对y0求偏导并忽略水平方向的影响可以得到水质点的垂直速度：

(5)

将式(5)对t求偏导得垂直加速度as：

(6)

所以负载所受的波浪力为

(7)

其中：

(8)

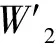
因此，入水前负载相对于地面坐标系以及入水时负载相对于地面坐标系的加速度分别为

(9)

(10)

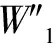
负载所受的浮力与负载的体积、质量以及液体的密度有关，所以负载的浮力为

Fv=ρgv

(11)

所以，入水前、入水时以及入水后缆绳的张力可以分别表示为

(12)

(13)

(14)

式中：Fs为缆绳张力；m为负载质量。

2 电驱动海洋牵引绞车控制系统的建立

2.1 牵引绞车的数学模型

牵引绞车的传递函数框图的建立如图2所示。

图2 牵引绞车传递函数框图

图中K1为变频器与电机之间的传递函数，即：

(15)

式中:N为变频器输出扭矩；U为模拟信号电压值。

K2为电机减速器的传递函数：

K2=iφ

(16)

式中：i为减速器减速比；φ为减速器传动效率。

在这里牵引绞车采用的是直接转矩控制方式进行力矩输出，则牵引绞车的力矩平衡方程为

(17)

式中：Mp为牵引绞盘扭矩；B为牵引绞盘黏性阻尼系数；J为牵引绞盘的转动惯量；Tr为牵引绞车初始入绳的张力；Tc为牵引绞车出绳张力；r为绞盘半径。

对式(3)进行拉普拉斯变换，则：

Mp=Bsθ+Js2θ+(Tr-Tc)r

(18)

式中:θ为牵引绞车绞盘转角。

因此，由式(18)得到绞盘转矩的传递函数G3(s)为

(19)

其中：

(20)

式中：K3为缆绳弹性系数；A为缆绳的截面积；E为缆绳弹性模量；L为下放缆绳长度；ΔL为缆绳伸长量。

2.2 牵引绞车PID控制

由于PID控制器使用方便、鲁棒性好以及可靠性高，因此被广泛应用于工业过程控制[17]。其原理是将给定输入与输出的偏差作为控制目标，通过调节比例、积分和微分系数来将偏差缩减至最小。但是其针对非线性、时变不确定性、强干扰等特性下的控制效果往往不好[18]。文中为了验证PID的控制效果，建立了PID控制器，其控制模型如图3所示。PID的控制规律为

图3 牵引绞车PID控制

(21)

式中：u(t)为控制器的输出信号；e(t)为偏差信号；k为采样次数；KP为比例系数；KI为积分系数；KD为微分系数。

2.3 牵引绞车模糊PID控制

模糊PID控制器由普通的PID和模糊控制器两部分组成。在海洋这种复杂的环境下，相较于普通PID控制，模糊PID控制可以适应这种非线性的状况，并且有一定的抗干扰能力。其中，模糊PID控制采用增量式，建立流程为：

第一步，输入值及输出值的模糊化。即对输入变量张力误差e(t)、张力误差变化率ec(t)输出变量ΔKP、ΔKI、ΔKD分别划分“NB”“NM” “NS”“ZO”“PS”“PM”“PB”7个模糊子集。同时确定e(t)、ec(t)、ΔKP、ΔKI、ΔKD的论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。另外，隶属度函数采用三角隶属度函数。

第二步，建立模糊规则表。即根据经验确定模糊控制语句来建立模糊规则，如表1所示。

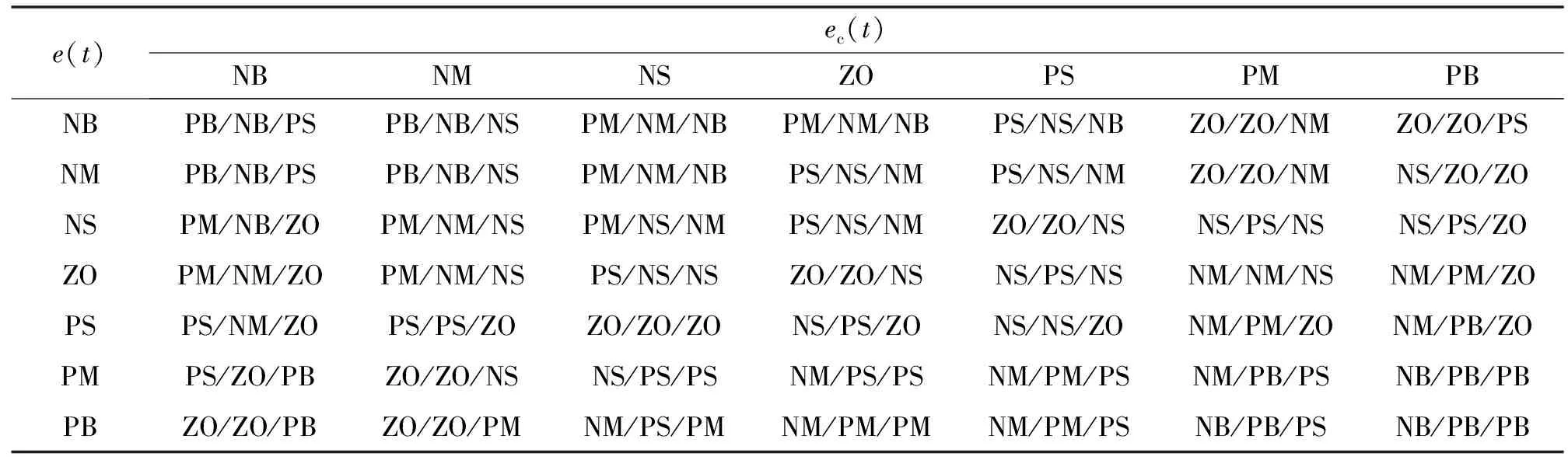
表1 ΔKP、ΔKI、ΔKD模糊控制规则

第三步，反模糊化。即将通过模糊推理得到的模糊量进行反模糊化处理，然后得到输出参数调整量ΔKP、ΔKI、ΔKD。反模糊化处理的方法采用加权平均法，其表达式为

(22)

式中：γ为重心值；x为语言变量的值；xmin，xmax为变量的范围；f(x)为隶属度函数公式。

将上述得到的参数调整量再乘以一定的系数与PID控制器的初始参数值相加，得到模糊PID的各个参数。其参数调整公式为：

(23)

式中：KP0、KI0、KD0为PID控制系统稳态时的参数；βP、βI、βD为比例因子；KP、KI、KD为模糊PID控制时的参数。

通过以上流程最终实现常规PID控制所没有的在线参数自整定功能。最终建立的控制模型如图4所示。

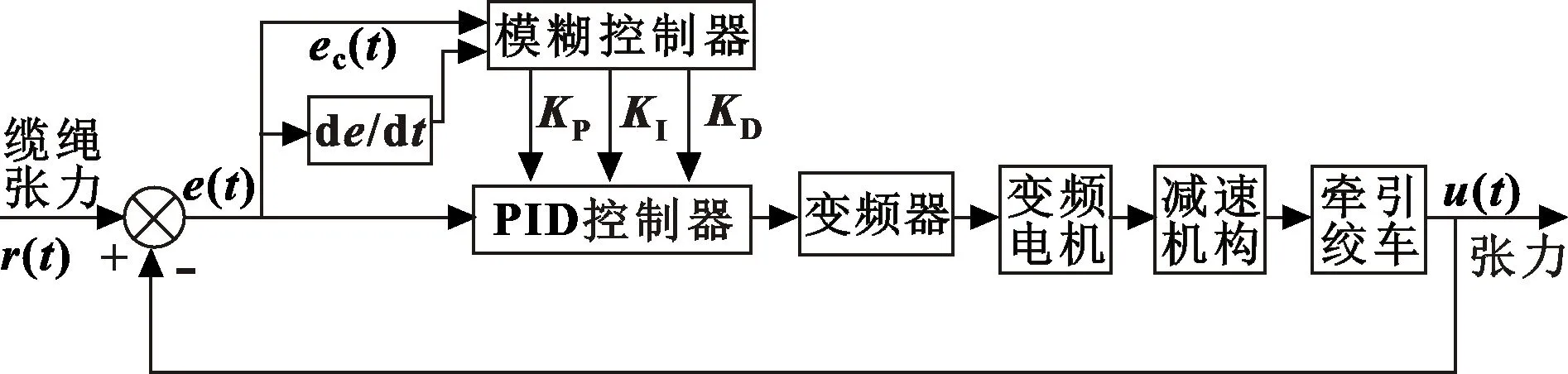
图4 牵引绞车模糊PID控制

2.4 牵引绞车BP模糊神经网络PID控制

由于模糊PID控制的自学习能力较差，而神经网络具有很强的自学能力，因此将BP神经网络与增量式模糊PID控制结合，建立一种弥补模糊PID控制自学习能力差的新的控制器，如图5所示。

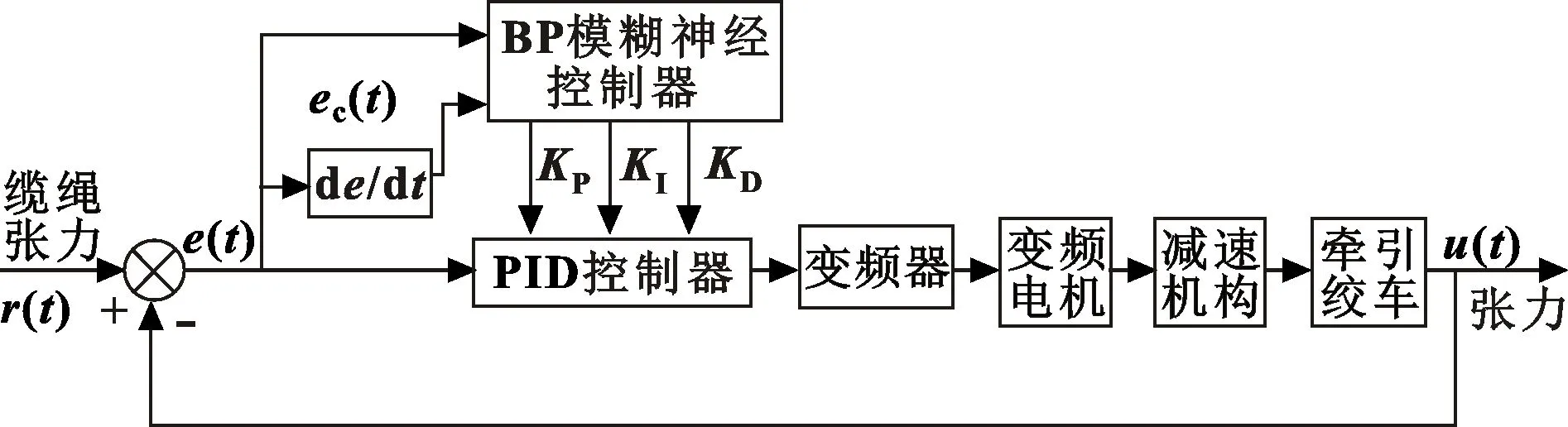
图5 牵引绞车BP模糊神经网络PID控制

BP神经网络模型的结构为2-7-49-49-3，如图6所示。

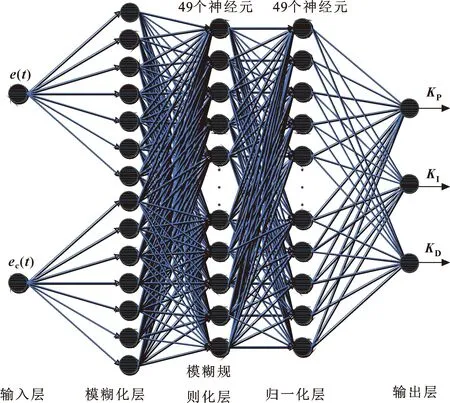
图6 BP模糊神经网络结构

输入层有两个输入，分别为误差e(t)及误差变化率ec(t)，输出的控制量为u(t)。在这里将这两个输入信号传入下一层可以表示为

(24)

下一层为模糊化层，共有7个单元节点，表示的是e(t)及ec(t)划分的“负大”至“正大”的7个隶属度函数，主要用来将其模糊化处理，则：

(25)

式中：mcd为第c个输入信号的第d个隶属度函数的均差；σcd为第c个输入信号的第d个隶属度函数的标准差。

第三层为模糊规则化层，每个神经元节点通过运算来表示规则的适应度Al，这里共计49条模糊规则，可以表示为

(26)

Nc为当层第c个节点。

第四层为归一化层，一共有49个神经元节点，作用是将第三层输出的49个神经元节点的值进行归一化计算。其计算方法为

(27)

输出层功能是将模糊化的输入经过规则化及归一化后进行反模糊化处理，计算方法为

(28)

其中，网络中误差函数为

(29)

式中：r(k)为期望输出；y(k)为实际输出。

文中BP模糊神经网络采用梯度下降法对mcd、σcd以及ωcd进行优化，其算法为

mcd(k+1)=mcd(k)+α(mcd(k-1)-

(30)

σcd(k+1)=σcd(k)+α(σcd(k-1)-

(31)

ωcd(k+1)=ωcd(k)+α(ωcd(k-1)-

(32)

式中：ηm、ησ、ηω分别为参数mcd、σcd以及ωcd的学习速率；α为动量因子。

3 仿真结果分析

基于表2所示参数，分别建立如图3—图4的仿真模型，得到如图7—图9的仿真结果。

表2 牵引绞车缆绳张力控制系统仿真参数

从图7—图9可以看到：在不规则波下搭载不同质量负载下放时，普通PID控制调节到稳态的时间约为0.27 s，并且出现了一定的超调；模糊PID控制调节的时间约为0.21 s并且没有超调；而在BP模糊神经网络PID控制下张力到达稳态的时间约为0.03 s。另外，文中对仿真模型施加了干扰来测试所设计的控制器在干扰情况下的反应速度以及稳态性能。

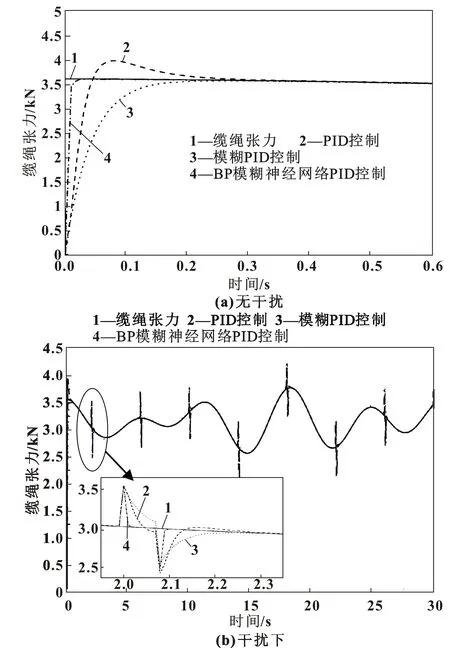
图7 不规则波下搭载300 kg负载缆绳张力控制

图8 不规则波下搭载600 kg负载缆绳张力控制

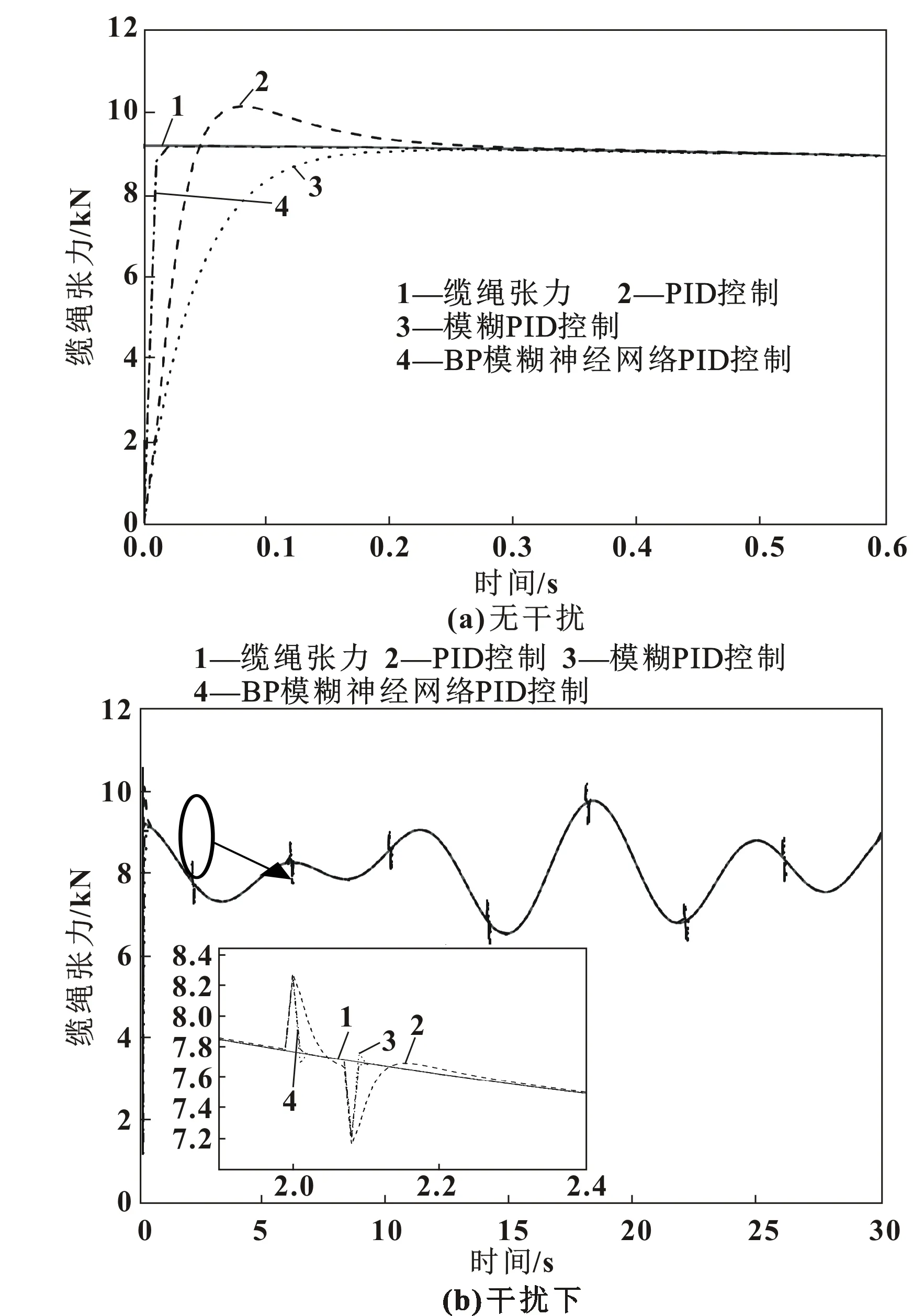
图9 不规则波下搭载800 kg负载缆绳张力控制

在仿真中从第2 s开始每4 s施加500 N的干扰力来测试控制器的反应速度及稳定性能。从图7(b)—图9(b)可以看到：当出现干扰时，BP模糊神经网络PID控制器调节反应的时间最快且调节时间最短，模糊PID控制器次之，传统PID控制的速度最慢；BP模糊神经网络控制下的震荡幅度最小，模糊PID控制下震荡幅值和BP模糊神经网络PID基本持平，普通PID控制的震荡幅值最大；图中，缆绳张力最大值出现在约t=17.5 s处。

4 结论

针对海浪等恶劣环境下，牵引绞车采用传统控制进行收放时所造成的缆绳过于松弛或张紧、缆绳张力不断震荡等情况，设计了基于BP模糊神经网络PID控制的牵引绞车张力控制器来对缆绳张力进行控制，以保证缆绳时时刻刻处于合适的张紧状态，实现在升沉作用下对负载收放时的补偿功能。另外，仿真验证了所设计的BP模糊神经网络PID控制器可以很好地实现缆绳的张力控制。通过仿真证明：相较于传统PID控制以及模糊PID控制，基于BP模糊神经网络PID控制的牵引绞车的张力控制效果稳定，在受到干扰时可以快速调整且精度最高。