考虑关节摩擦的刚柔耦合机械臂末端抖动模拟与分析

管恋哲，张振山，崔国华，潘颖

(上海工程技术大学机械与汽车工程学院，上海 201620)

0 前言

机器人作为一种典型的机电一体化产品，在现代生产生活中有十分重要的作用，其应用场景不但涉及汽车、机床等工业领域，而且在航空、医疗以及家政服务等方面也应用广泛[1-2]。但在焊接、装配、去毛刺等操作过程中，其末端容易发生抖动[3]，从而导致机器人实际的运动性能与期望的高精度运动性能相比还有较大的差距[4]。为了满足轻型制造任务等需要[5]，对机器人的末端抖动进行研究十分必要。其中，机器人关节摩擦的存在会影响机器人控制系统的质量，从而造成系统动荡。对于做轨迹追踪的机械臂来说，当突然改变速度方向时，摩擦会造成机械臂较大的追踪误差和出现极限环振荡[6]；对于低速工作的机械臂来说，摩擦力矩的存在会造成其产生爬行现象及追踪滞后[7],机械臂工作所需的驱动力矩大约有20%消耗在克服摩擦阻力上[8]。

山显雷、程刚[9]以3SPS+1PS并联机构为研究对象，基于牛顿-欧拉法，通过选取动平台上球铰链所在位置点的运动学参数作为中间变量，建立了考虑关节摩擦且具有显式形式的动力学模型，并验证了所建模型的有效性，所得模型可用于并联机构的摩擦补偿控制研究。段书用等[10]以六轴串联机械臂为研究对象，基于拟非线性摩擦模型与斯特里贝克效应，建立了机械臂关节非线性摩擦模型，研究了摩擦模型对末端运行轨迹的影响，结果表明：在关节角速度较低时摩擦对末端轨迹的非线性影响较大，反之影响较小；关节2对末端轨迹影响较小；关节3和4对机械臂末端轨迹影响较大。杜志江等[11]以某机械臂的高速轴与低速轴为研究对象，提出一种同时考虑摩擦、间隙和迟滞的综合建模方法，并将所建立的模型在MATLAB/Simulink中进行了验证，结果表明所建立的模型可以有效仿真出实际关节的各种非线性特性。刘才山等[12]针对重力场下作大范围回转运动的柔性梁与一固定斜面发生斜碰撞的情况，基于假设模态法与刚柔耦合效应的多柔体系统动力学建模理论，提出了考虑摩擦作用的多柔体系统的点-面碰撞模型，为解决具有变拓扑结构的多体系统动力学问题奠定了理论基础。刘福才等[13]以二自由度机械臂为研究对象，建立了考虑摩擦和不考虑摩擦情况下机械臂的动力学模型，并采用PD算法对两种情况下的动力学模型进行仿真研究，结果表明：摩擦对控制机械部运动的驱动力以及轨迹追踪精度所产生的影响与重力密切相关，与重力大小呈正相关。

传统的多体系统动力学研究主要围绕多刚体构件进行，但随着现代机械化及工作精度要求的提高，考虑刚性运动及其运动变形之间的耦合作用的弹性动力学问题，已成为目前的研究热点[14]。仅运用刚体动力学或弹性力学都无法准确描述构件的刚性运动及弹性变形之间的耦合作用[15]，故运用刚柔耦合体进行动力学仿真更接近真实情况。

本文作者采用虚拟样机软件ADAMS和有限元分析软件ANSYS联合建立一种六自由度串联机械臂的刚柔耦合模型，并进一步考虑关节摩擦，对机器人进行动力学仿真，从而分析了单关节摩擦与多关节摩擦对机器人末端抖动的影响，为研究机器人的振动特性和设计改进提供了参考。

1 刚柔耦合振动模型的建立

基于ANSYS和ADAMS建立的刚柔耦合机械臂模型原理图如图1所示。用SolidWorks建立机构的实体模型，然后导入到ADAMS中；在ADAMS环境下给实体定义材料属性、添加约束、施加驱动，在后处理过程中可列出各个构件所受的外加载荷、约束反力和惯性力；通过ANSYS对其进行受力分析以寻找薄弱环节，并将薄弱环节离散成小网格，然后进行模态计算；计算的模态中性文件以MNF(模态中性文件)形式重新导入ADAMS里替换刚性体，最终建立整个系统的刚柔耦合模型。

图1 基于ANSYS和ADAMS建立的刚柔耦合机器人模型原理 图2 刚柔耦合机器人模型

在进行六自由度串联机器人振动规律的研究时，把与机器人末端抖动关系密切、变形较大的部件采取柔性化处理，即把机器人大臂、小臂及腰关节考虑为柔性体，其余变形量小且与机器人末端抖动联系较少的部件仍处理为刚体。图2所示为刚柔耦合机器人模型。

2 关节摩擦对机器人末端抖动的影响

2.1 单关节摩擦对机器人末端抖动的影响

图3—图8所示为各关节单独存在摩擦时机械臂末端的加速度响应，从图3中可以得出：当机器人各关节都不存在摩擦的理想状态下，在机器人的整个运行工况中，其末端的抖动基本在±10 m/s2的范围内波动，且波动的频率相对较低。图4所示为关节1存在摩擦时机器人末端抖动加速度响应情况，可知：在机器人运行0～1 s内其末端抖动最为剧烈，在±10 m/s2范围内波动，1 s后，机器人末端抖动加速度响应明显降低，并在后续运动过程中趋于平缓。图5所示为关节二存在摩擦时机器人末端抖动加速度响应，可知：当机器人关节2存在摩擦时，机器人末端抖动频率高，且抖动幅值大，在0～1 s其末端抖动在±125 m/s2范围内波动，1～4 s内机器人末端抖动幅值显著增加，且在-335～475 m/s2范围内波动，4 s后，机器人末端抖动幅值突然减小，且趋于平缓，其抖动幅值在±168 m/s2范围内变化。图6所示为关节3存在摩擦时机器人末端抖动加速度响应情况，可知：机器人在0～1.17 s内末端抖动剧烈，抖动频率高，且在0.49 s时其末端抖动幅值最大，为506 m/s2(图中未示出)；在0.49 s之后，末端抖动逐渐减小，且在1.17 s后在0上下小范围波动，此时机器人末端抖动基本可以忽略不计。图7所示为关节4存在摩擦时机器人末端抖动加速度响应情况，可知：关节4对机器人末端抖动的影响较小，0～1 s内抖动幅值在-6～9 m/s2范围内变化，1 s后机器人末端抖动幅值减小，且抖动频率也较小，在±2.5 m/s2范围内变化。图8所示为关节5存在摩擦时机器人末端抖动加速度响应情况，可知：机器人末端抖动幅值基本稳定在±6 m/s2范围内变化，且波动频率较低。

图3 无关节摩擦时机器人末端抖动情况

图4 关节1存在摩擦时机器人末端抖动情况

图5 关节2存在摩擦时机器人末端抖动情况

图6 关节3存在摩擦时机器人末端抖动情况

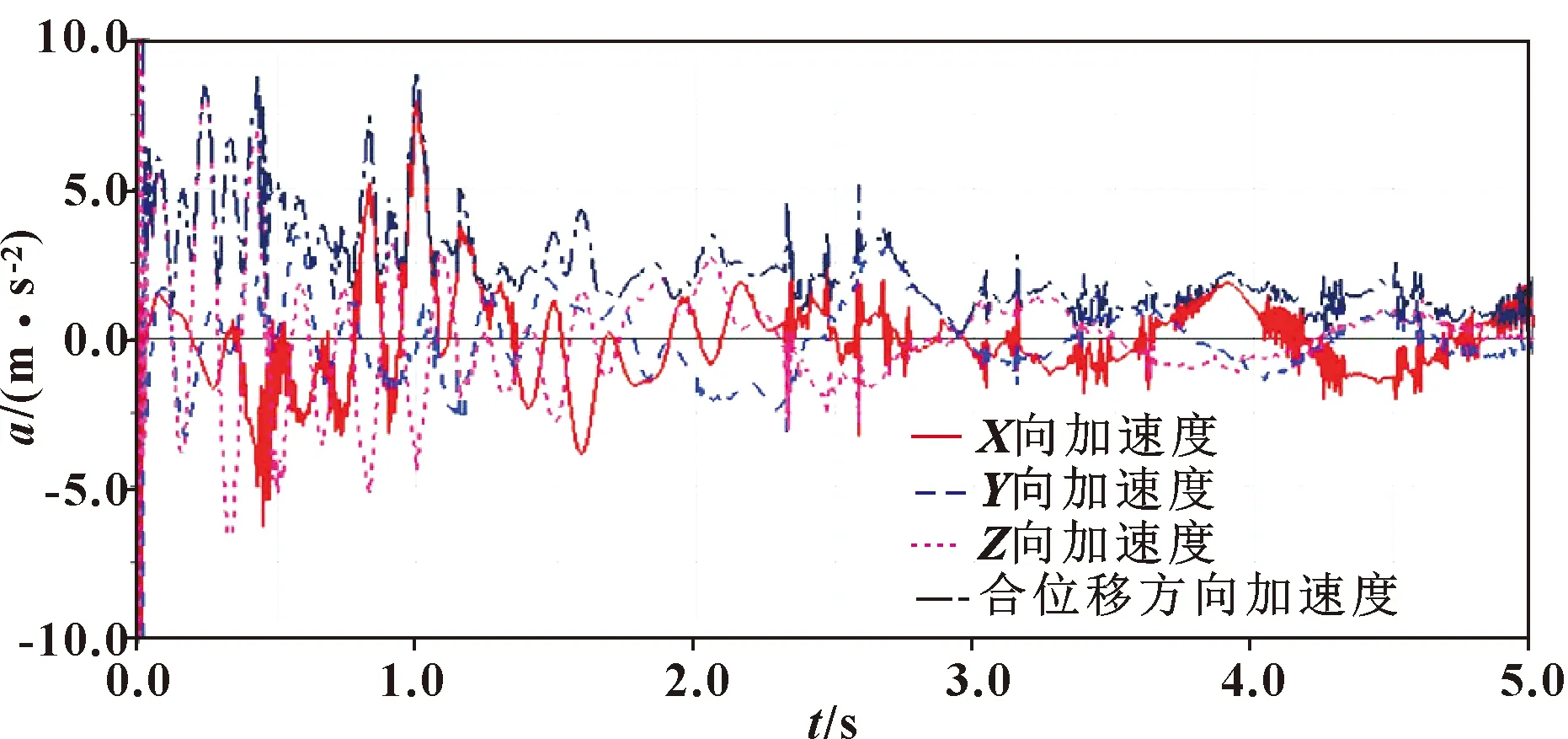
图7 关节4存在摩擦时机器人末端抖动情况

图8 关节5存在摩擦时机器人末端抖动情况

综上所述：机器人关节1、关节4、关节5存在关节摩擦时，对机器人末端抖动幅值的影响较小；而关节2、关节3存在关节摩擦时，机器人末端抖动幅值发生剧烈变化，且抖动频率也会显著增加。机器人运动过程中，关节摩擦无法避免，其对机构的运动有显著的影响。关节摩擦不仅会造成能量损耗，同时也会对机器人的动力学特性造成影响。由于关节2与关节3对机器人末端抖动影响较大，故将进一步考虑两个关节摩擦同时存在的情况下，机器人末端的抖动情况。

2.2 多关节摩擦对机器人末端抖动的影响

图9所示为所有关节同时存在摩擦时机器人末端抖动加速度响应情况，可知：在0～1.57 s时段内，机器人末端抖动幅值小；在1.57 s之后，机器人末端抖动剧烈，抖动幅值整体在-1 200～1 790 m/s2内变化。结合图3可得：所有关节同时存在摩擦，会加剧机器人末端抖动。

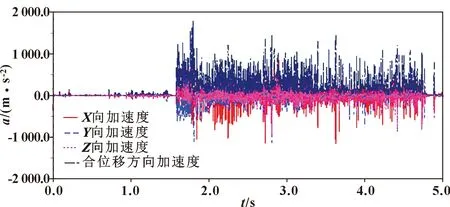
图9 所有关节存在摩擦时机器人末端抖动情况

图10所示为关节2与关节3同时存在摩擦时机器人末端抖动加速度响应情况，2.096 5～2.2 s时段内机器人抖动最剧烈，抖动范围为-560～900 m/s2；其次为3.3～3.7 s时段，抖动范围为-336～650 m/s2；而在其余时段，机器人末端抖动幅值趋于平稳，基本在±50 m/s2附近变化。结合图5、图6可知：当关节2与关节3同时存在摩擦时，机器人末端抖动幅值明显减小。主要是由于关节摩擦的存在造成了系统的能量损耗，从而造成了机器人加速度幅值的减小。

图10 关节2和关节3存在摩擦时机器人末端抖动情况

3 摩擦因数大小对机器人末端抖动的影响

为进一步研究关节2与关节3的摩擦力大小对机器人末端抖动的影响，设置摩擦因数分别为0.07、0.1、0.13，其他参数值相同的情况下，对刚柔耦合机械臂系统进行动力学仿真分析。

3.1 关节2摩擦因数大小对机器人末端抖动的影响

图11—图13分别为关节2摩擦因数为0.07、0.1、0.13时机器人末端抖动情况。由图11可知：当摩擦因数为0.07时，机器人末端抖动加速度幅值最大为1 723 m/s2，工作时段基本在±540 m/s2附近波动。由图12可知：当摩擦因数为0.1时，机器人末端抖动加速度幅值最大为470 m/s2，且整体抖动相对平稳，基本保持在±350 m/s2内变化。由图13可知：当摩擦因数为0.13时，机器人末端抖动加速度幅值最大为574 m/s2(图中未示出)，整体抖动范围为±392 m/s2。综上分析，当关节2摩擦因数为0.1时机器人末端抖动表现最弱。

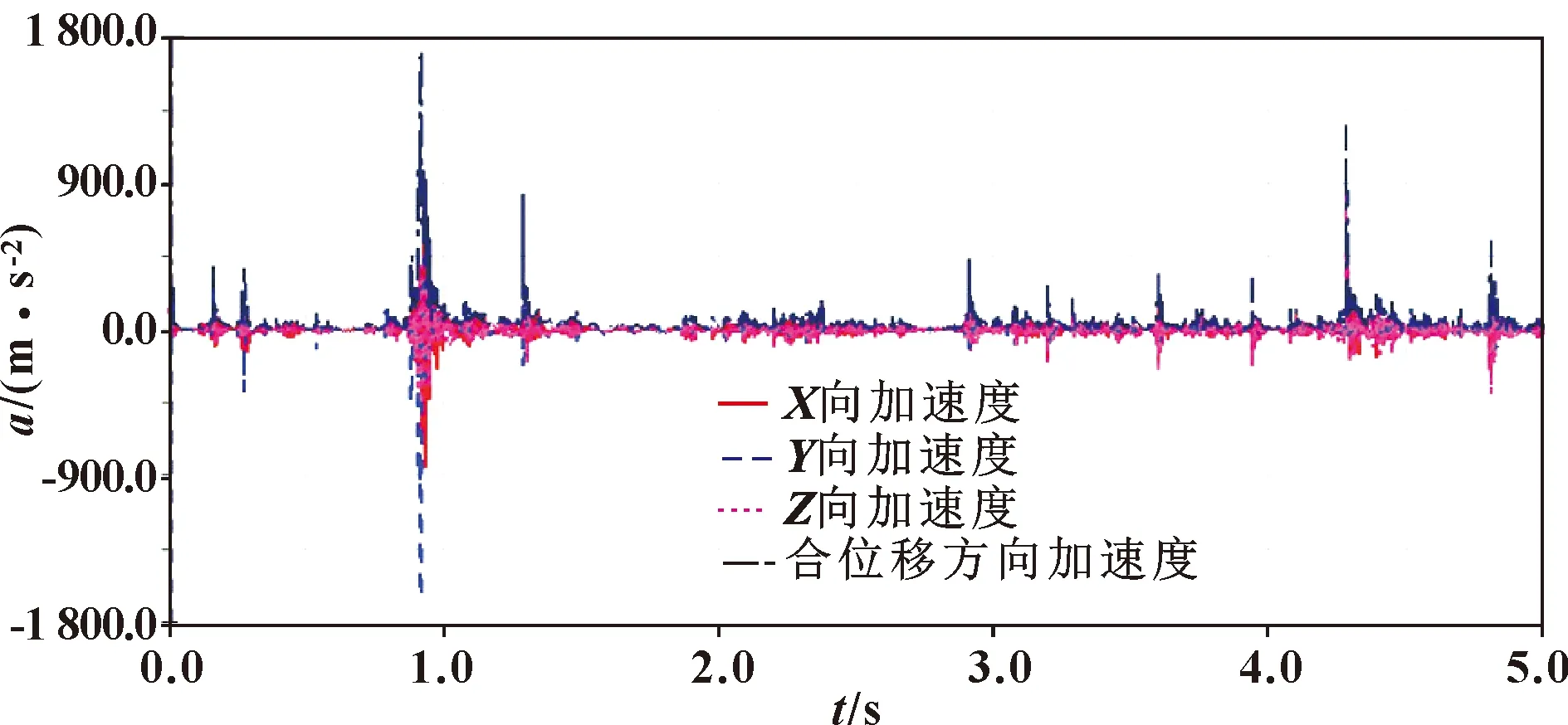
图11 关节2摩擦因数为0.07时机器人末端抖动情况

图12 关节2摩擦因数为0.1时机器人末端抖动情况

图13 关节2摩擦因数为0.13时机器人末端抖动情况

3.2 关节3摩擦因数大小对机器人末端抖动的影响

图14—图16分别为关节3摩擦因数为0.07、0.1、0.13时机器人末端抖动情况。可得：摩擦因数的改变，只引起了0.99～1.18 s时段内机器人末端抖动幅值的极小变化。故可得出机器人关节3摩擦因数的改变几乎不会引起机器人末端抖动幅值的改变。

图14 关节3摩擦因数为0.07时机器人末端抖动情况

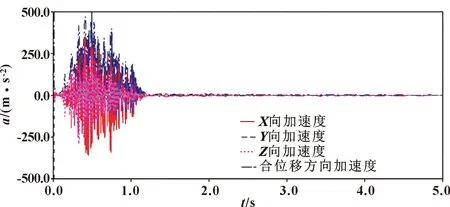
图15 关节3摩擦因数为0.1时机器人末端抖动情况

图16 关节3摩擦因数为0.13时机器人末端抖动情况

4 结论

利用ADAMS和ANSYS联合仿真建立六自由度机械臂的刚柔耦合模型，对其进行动力学仿真，分析单关节摩擦与多关节摩擦对机器人末端抖动的影响，得出以下结论：

(1)该六自由度串联机械臂实际工作过程中，关节2、关节3存在摩擦时对机器人末端抖动的影响最显著。

(2)机器人所有关节同时存在摩擦时，会加剧机器人末端抖动情况。但当只有关节2和关节3同时存在摩擦时，机器人末端抖动情况得到明显改善，抖动剧烈时段大大缩短，抖动幅值也明显降低。

(3)随着摩擦因数的增大，机器人末端抖动幅值随之减小，但机器人末端抖动幅值不会随着摩擦因数的增大而无限度减小，摩擦因数只有在一定的范围内进行取值，机器人末端抖动才会得到有效改善。关节2摩擦因数为0.1时机器人末端抖动表现最弱。但关节3摩擦因数的改变几乎不会引起机器人末端抖动情况的变化。