永磁同步电机定子系统模型等效方法与模态分析

王 超，孙 悦

永磁同步电机定子系统模型等效方法与模态分析

王 超，孙 悦

（中汽研（天津）汽车工程研究院有限公司，天津 300000）

为了准确地预测电机定子系统的模态特性和各阶固有频率，文章提出了一种永磁同步电机定子系统模型等效方法并进行模态分析。首先，利用有限元方法建立定子铁心及绕组模型，设置各向异性材料属性；然后，通过仿真计算得到定子铁心及绕组的固有频率，并进行模态分析。最后，利用锤击法模态试验验证定子系统模型等效方法的准确性。文章为电机定子系统的模态分析提供了新的等效分析方法，提高了计算精度。

永磁同步电机；定子系统模型；模型等效方法；模态测试；模态分析

新能源汽车快速发展，车用永磁同步电机的噪声、振动与声振粗糙度（Noise, Vibration, Harsh- ness, NVH）问题越来越多地引起人们的关注[1-4]。准确预测电机定子系统的模态特性和各阶固有频率，是抑制新能源汽车驱动电机NVH问题的关键[5-7]。

由于电机结构越来越复杂，定子铁心的硅钢片叠压工艺，绕组的复杂装配工艺等因素，使得传统计算预测模态特性和固有频率方法的结果与实际存在很大误差。随着有限元软件的发展，有限元分析与试验相结合的方法是目前最有效的方式。

近些年来国内外很多学者都对电机定子系统模态进行了分析。文献[8]针对叠片效应将铁心视为一种均质的正交各向异性层压板结构材料，之后对绕组部分设置材料属性，结合仿真和试验验证了方法的准确性。文献[9]介绍了一种简单且无损的杨氏模量测量方法，使得电机铁心刚度大，计算结果与真实情况相比较为准确。然后将其用于有限元程序中，以确定开关磁阻电机（Switched Reluctance Motor, SRM）定子振动的共振频率，文章还讨论了质量密度和泊松比的影响。文献[10]分析了定子铁心和绕组的等效模型，总结等效模型材料参数对定子铁心固有频率的影响，提出了一种快速确定等效模型材料参数的方法。文献[11]确定等效模型材料参数的方法，进行了定子铁心和绕组系统的四种有限元模型对比，得出了一种新型的定子系统有限元等效模型。

总之，已经有很多学者对电机定子铁心-绕组系统进行了研究。然而，在定子系统模型等效方法上存在差异，导致无法准确计算出电机各阶固有频率；并且在电机的模态分析中，带绕组系统的定子系统0阶模态是分析研究的关键，对于电机的NVH性能有直接的影响，但一般有限元方法很难计算出铁心-绕组系统的0阶模态。

本文以一台车用永磁同步电机为研究对象，分析定子铁心及定子绕组系统的模态特性与固有频率，考虑定子铁心的各项异性材料属性对定子铁心和绕组系统固有频率的影响，并利用有限元软件建立一种绕组等效模型，此方法既能够有效提升计算速度，又能减小模型固有频率的计算误差。最后利用模态试验验证理论分析和绕组等效方法的准确性。

1 有限元方法建模与模态分析

有限元方法可以精确地建立电机定子铁心和绕组系统的复杂模型，并使其尽可能地与实际电机一致，计算精度较高。由于电机转子模态固有频率对定子系统的模态参数影响很小，因此，在有限元建模时不考虑转子[12]。

1.1 定子铁心的建模与模态分析

根据实际定子铁心形状进行准确的有限元建模，如图1所示。考虑到定子铁心由硅钢片叠压而成，有限元建模时将铁心的材料属性等效为各向异性材料，等效模型的材料属性如表1所示。其他参数根据式（1）—式（3）计算得出[13]。

E=E（1）

v=v（2）

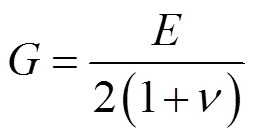
表1 铁心等效材料属性

各向异性参数符号数值 密度ρ/(g/m3)7.945 弹性模量Ex/MPa245 000 Ez/MPa1 000 泊松比vxy0.3 vxz0.3

有限元方法计算结果见表2，其中（，）表示阶径向模态，阶轴向模态。由表2可知，采用各向异性材料属性能够有效地计算出定子铁心各阶模态振型和固有频率，尤其是能够计算出定子铁心的0阶模态，这对于后面的定子铁心-绕组系统的研究和频率分析有重要意义。

1.2 绕组的建模

由于绕组的材料为铜，受槽满率、浸漆工艺及绝缘层的影响，弹性模量等材料属性很难确定；并且由于绕组的端部结构复杂，建模难度较大。所以绕组的建模是电机模态分析中的重点和难点。

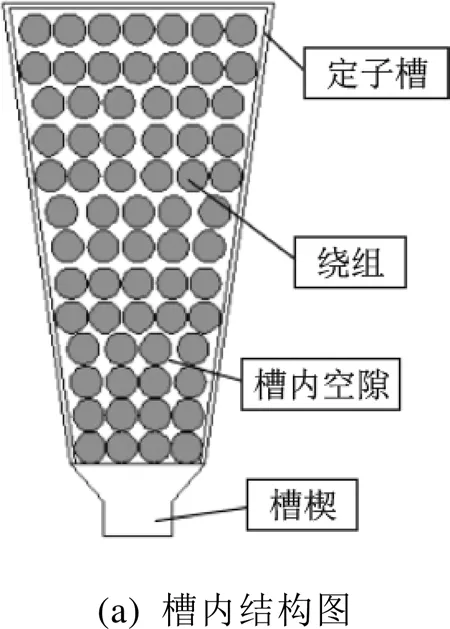
定子绕组系统由多个部分组成（导体、导体涂层、槽内空隙等），可以等效成各向异性材料。为简化计算，便于分析，我们做如下假设[10]：

（1）所有导体的尺寸都是恒定的且平行铺在槽中；

（2）导体有规律地充满定子槽；

（3）导体之间没有相对移动；

（4）导体本身无相对变形。

表2 定子铁心仿真模态振型和固有频率

振型（m,n）定子铁心结构固有频率/Hz （2,0）894 （3,0）2 431 （4,0）4 438 （5,0）6 781 （0,0）7 036

故建立如下绕组等效模型，如图2所示。

1.3 定子铁心-绕组系统的建模与模态分析

在定子铁心模型的基础上，在定子槽中加入绕组等效模型进行建模，如图3所示。定子铁心-绕组系统等效材料参数如表3所示。

图3 定子铁心-绕组系统模型

表3 定子铁心-绕组系统等效材料属性

各向异性参数符号数值 密度ρ/(g/m3)15.66 弹性模量Ex/MPa2 500 Ez/MPa2 500 泊松比vxy0.3 vxz0.3

通过以上定子铁心-绕组系统进行等效后，进行有限元分析得到结果见表4。

表4 定子铁心-绕组系统仿真模态振型和固有频率

振型（m,n）定子铁心结构固有频率/Hz （2,0）832 （3,0）2 235

表4 （续）

（4,0）4 065 （5,0）6 189 （0,0）6 526

1.4 绕组对电机定子系统模态固有频率的影响

定子铁心仿真结果和定子铁心-绕组系统仿真结果对比如图4所示，可知加入绕组后电机定子系统模态的固有频率会有一定程度的下降。定子-绕组系统阶径向振动模态的固有频率可表示为

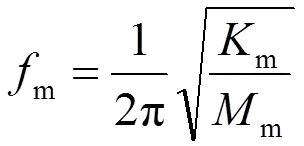
式中，m为定子-绕组系统的集中刚度，N/m；m为定子-绕组系统的集中质量，kg。

由于绕组的等效刚度远远低于定子铁心，所以在定子系统加入绕组后，对集中刚度m的贡献量很小，集中质量m却大为提高。结果就会导致固有频率m有所降低。因此，在电机NVH性能优化时，可以通过增加绕组刚度、减少绕组质量来提高电机定子系统的固有频率，例如将传统的圆线绕组改为扁线绕组，在相同条件下可以提高电机定子系统的0阶模态固有频率，从而减少或避免由电机固有频率与其他系统频率耦合而发生共振导致的NVH问题。

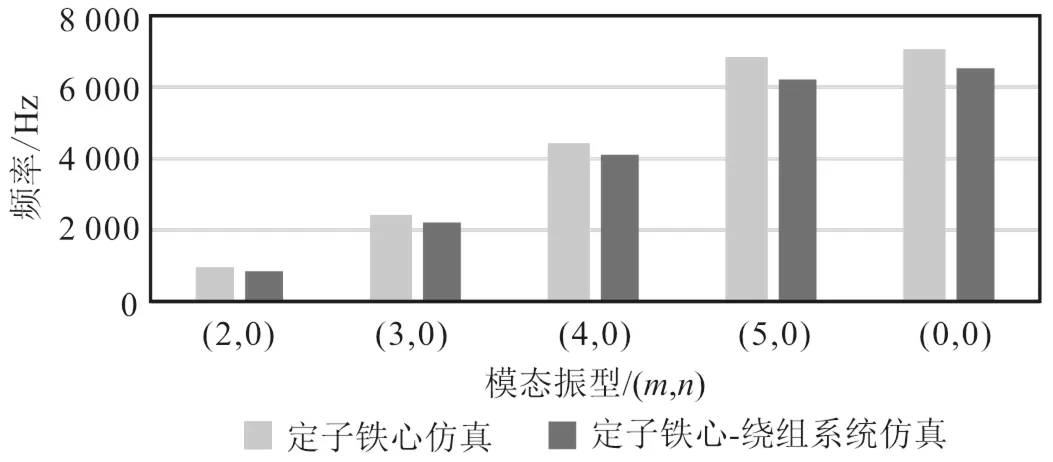
图4 定子铁心和定子铁心-绕组系统仿真结果对图

2 模态试验验证

2.1 定子铁心模态试验

为了验证有限元仿真的准确性，采用锤击法对定子铁心进行模态试验测试。测试采用Siemens LMS前端设备进行数据采集，使用LMS Test.Lab 14A软件进行信号处理模态分析。被测试的定子铁心用软绳悬挂在空中以模拟其自由状态，尽可能与有限元仿真环境一致。在定子铁心径向选取9个测点布置三向振动加速度传感器，轴向选取3列，共计27个测点，然后利用力锤进行敲击测试，测试图片见图5。测试结果见表5。

图5 定子铁心自由模态试验

表5 定子铁心模态试验振型和固有频率

振型（m,n）定子铁心结构固有频率/Hz （2,0）894 Hz894 （3,0）2 451 Hz2 451 （4,0）4 418 Hz4 418 （5,0）6 689 Hz6 689 （0,0）7 058 Hz7 058

2.2 定子铁心-绕组系统模态试验

与定子铁心模态试验类似，定子铁心-绕组系统同样采用锤击法进行模态试验测试。测试采用Siemens LMS前端设备进行数据采集，使用LMS Test.Lab 14A软件进行信号处理模态分析。被测试的定子铁心用软绳悬挂在空中以模拟其自由状态。在定子铁心径向选取9个测点布置三向振动加速度传感器，轴向选取3列，共计27个测点，然后利用力锤进行敲击测试，测试图片见图6。测试结果见表6。

图6 定子铁心-绕组系统自由模态试验

表6 定子铁心-绕组系统模态试验固有频率

振型（m,n）固有频率/Hz （2,0）838 （3,0）2 123 （4,0）4 289 （5,0）6 179 （0,0）6 534

测出的模态振型和固有频率，与有限元计算的结果对比，如图7所示。定子铁心仿真与试验测试固有频率误差，如图8(a)所示。定子铁心-绕组系统仿真与试验测试固有频率误差，如图8(b)所示。定子铁心仿真与试验测试最大误差1.4%。定子铁心-绕组系统仿真与试验测试最大误差5.3%。可知，有限元仿真与试验测试结果较为吻合，验证了有限元模型的正确性，基本可以满足工程需要。

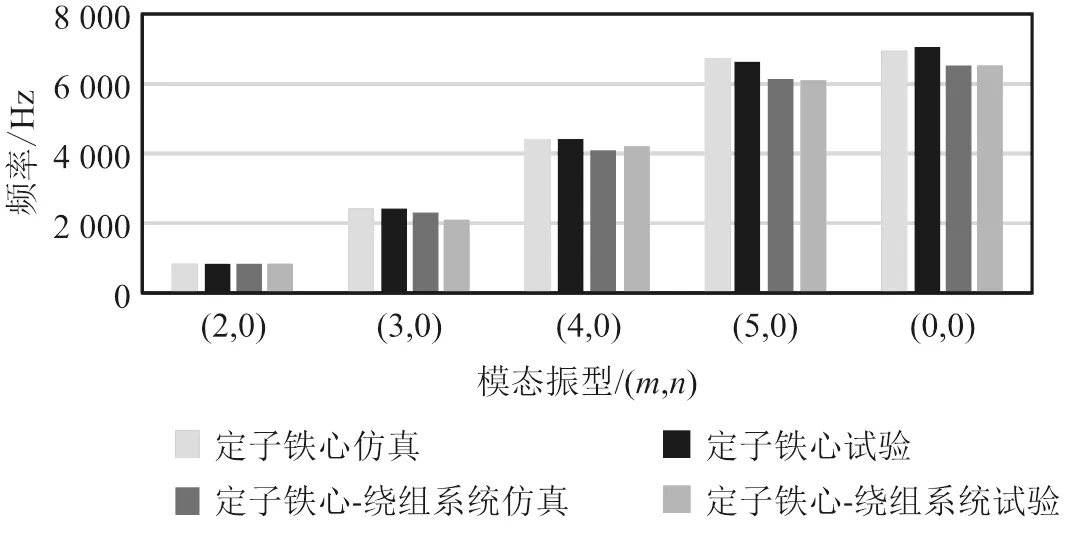
图7 有限元法与试验固有频率结果对比

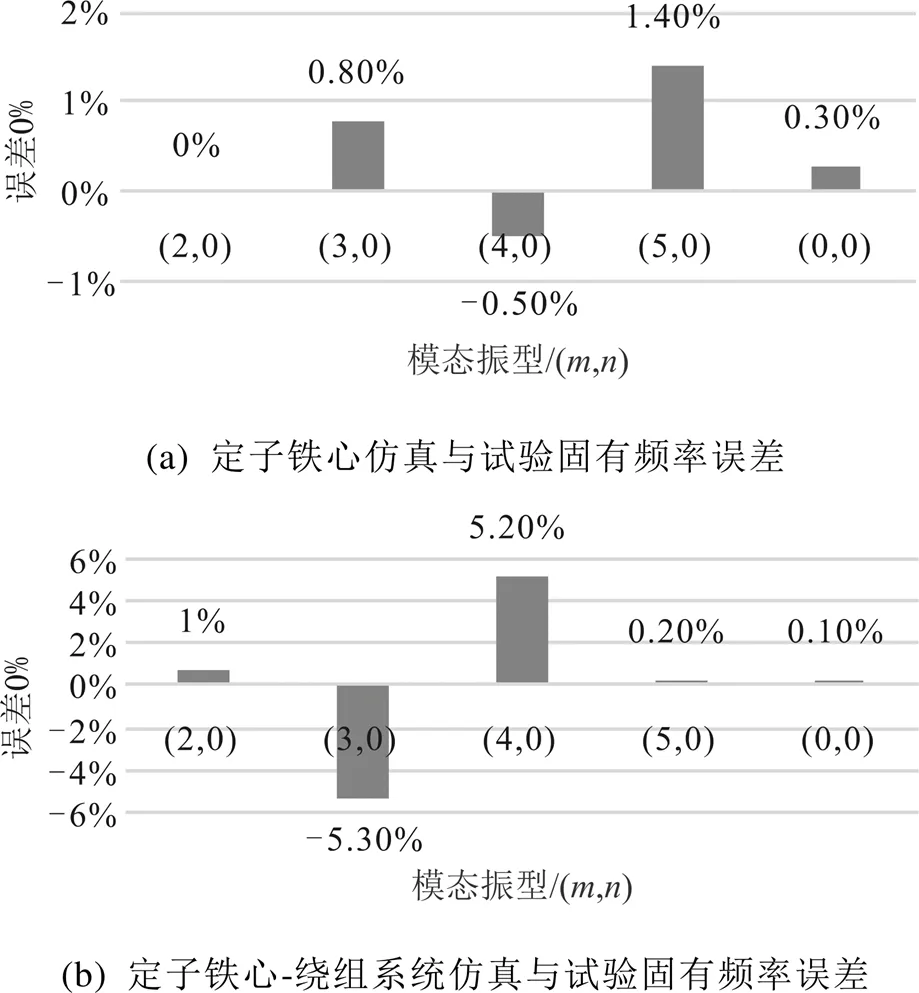
图8 有限元法与试验固有频率误差对比

3 总结

本文主要研究分析了永磁同步电机定子铁心和定子铁心-绕组系统的有限元模型等效问题，提出了一种绕组等效模型的方法。首先，利用有限元仿真分析获取定子铁心各向异性材料参数；然后，利用有限元方法建立绕组等效模型，计算定子固有频率并进行模态分析；最后，利用模态试验对有限元法进行分析验证。本文得到以下结论：

（1）增加绕组刚度和减少绕组质量，能够提高定子系统的固有频率，从而减少或避免由电机共振产生的新能源汽车NVH问题。

（2）本文介绍的等效模型方法中定子铁心与定子铁心-绕组系统的仿真数据与试验数据最大误差分别为1.4%和5.3%，验证了等效模型方法的合理性及仿真的准确性。

[1] MA F,YIN H,WEI L,et al.Design and Optimization of IPM Motor Considering Flux Weakening Capability and Vibration for Electric Vehicle Applications[J]. Sustainability,2018,10(5): 1533.

[2] MA F,YIN H,WEI L,et al.Analytical Calculation of Armature Reaction Field of the Interior Permanent Magnet motor[J]. Energies, 2018,11(9):2375.

[3] WANG Y C,GAO H,WANG H Y,et al.NVH Optimiza- tion Analysis of Permanent Magnet Synchronous Motor by Rotor Slotting[J].Vehicles,2020,2(2):287- 303.

[4] ACEK F G,CHONG W,JOSEPH C L.Noise of Polyp- hase Electric Motors[M].New York:CRC Press,2005.

[5] 林巨广,吴梦.基于模态分析的永磁同步电机噪声研究[J].机械设计, 2020,37(3):33-38.

[6] 高辉,尹红彬,王永超.不同槽极数配合的永磁电机噪声特性分析[J].微电机,2019,52(3):1-4.

[7] WU S L,ZUO S G,WU X D.Vibroacoustic Prediction and Mechanism Analysis of Claw Pole Alternators[J]. IEEE Transactions on Industry Electronics,2017,4(6): 4463-4473.

[8] 陈云华,丁天慧,田磊.电机叠片铁心的振动特性计算方法研究[J].电机与控制学报,2014,18(1):71-76.

[9] TANG Z J,PILLAY P, AVOKI M,et al.Young's Modu-lus for Laminated Machine Structures with Particular Reference to Switched Reluctance Motor Vibrations [J]. IEEE Transactions on Industry Applications,2004, 40(3):748-754.

[10] YIN H,MA F,ZHANG X, et al.Research on Equivalent Material Properties and Modal Analysis Method of Stator System of Permanent Magnet Motor with Concentrated Winding[J].IEEE Access,2019(7):64592- 64602.

[11] YIN H,MA F,ZHANG X, et al.New Equivalent Model and Modal Analysis of Stator Core-Winding System of Permanent Magnet Motor with Concentrated Winding[J]. IEEE Access, 2020,8:78140-78150.

[12] WANG C,LAI J C S.Vibration Analysis of an Induc- tion Motor[J].Journal of Sound and Vibration, 1999, 224(4):733-756.

[13] JSOL.JMAG-Designer 16.0.Help[M].Tokyo:JSOL,2019.

Equivalent Method and Modal Analysis of Stator System Model of Permanent Magnet Synchronous Motor

WANG Chao, SUN Yue

( CATARC (Tianjin) Automotive Engineering Research Institute Company Limited, Tianjin 300000, China )

In order to accurately predict the modal characteristics and natural frequencies of the stator system of the motor,in this paper, an equivalent method of permanent magnet synchronous motor stator system model is proposed and its modal analysis is carried out. Firstly, the stator core and winding model are established by finite element methods, and an anisotropic material attribute is set.Then, the naturalt frequency of the stator core and the windings is obtained by simulation, and modal analysis is performed. Finally, the accuracy of the equivalent method of the stator system model is verified using hammer method modal test. This article provides a new equivalent analysis method for the modal analysis of the motor stator system, and improves the calculation accuracy.

Permanent magnet synchronous motor; Stator sysiem model;Model equivalent method; Modal test; Modal analysis

10.16638/j.cnki.1671-7988.2022.021.004

U469.72

A

1671-7988(2022)21-19-06

U469.72

A

1671-7988(2022)21-19-06

王超（1991—），男，工程师，研究方向为新能源电驱动系统，E-mail:wangchao@catarc.ac.cn。