基于有限元法的点线啮合齿轮动力学模态分析研究

栾阔

基于有限元法的点线啮合齿轮动力学模态分析研究

栾阔

（皖江工学院 机械工程学院，安徽 马鞍山 243031）

：使用ANSYS的未激励齿轮的齿廓、周期变化、APDL语言建立了齿轮系统的虚线网格的参数模态分析模型。采用APDL线性点网格分析表定义了一个特殊的界面，输入参数并自动读取，调用分析仪并执行动态差计算。通过分析固有频率与阶数之间关系来反映点线啮合齿轮动力学模态变化过程，以及通过压力角与阶数之间关系折射出对模态的影响过程。此分析程序的开发对点线啮合齿轮拟态的分析和设计能力奠定了强有力的基础。

ANSYS；APDL语言；点线啮合齿轮；模态分析

齿轮作为机械工业中的重要基础件，点线啮合齿轮属于一种新型齿合传动形式，虽然也是渐开线齿轮，但工作齿廓和啮合状态与未分开齿轮的啮合位置存在些许相似。啮合过程中既存在线接触也存在点接触，点线啮合齿轮是一个特殊的齿轮形式，排量大，没有咬边，使得虚线上的测量设备变得越来越复杂，外加凹齿轮和凸齿轮的啮合使得设备具有更大的承载能力，因此研究点线啮合齿轮在动力学模态上的变化过程具有一定的研究意义[1-4]。本文基于有限元方法分析研究在点线啮合齿轮动力学中有关固有频率、阶数以及压力角等因素对模态变化的影响，可为类似研究提供借鉴意义。

1 ANSYS软件和点线啮合齿轮理论

1.1 APDL参数化建模方法

ANSYS有两种使用形式，一种是GUI模式，另一种是使用APDL编程语言。APDL因丰富的语法功能，可实现更加自由的情景模拟，从而成为ANSYS最重要的开发工具。使用APDL编程语言和宏观经济命令来计划和管理ANSYS，可以生成模型，参数计算和变量过程可以通过添加模态参数分析来实现加载并解算最大，并在处理后显示结果。

1.2 点线啮合齿轮理论

基于Litvin对人造表面形成原理的研究，提出了一种制造带有一对相互连接母表面的斜齿轮的方法。假设有两个刚性的母表面可以完全相互连接，并且每个母表面都被包裹和成形，两条虚线与齿轮的齿面缠绕在一起。图1表示了待加工齿轮的齿面与工具的齿面（凹面）的相对位置和相互运动。齿轮1、2分别以1和2的速度绕轴1和2旋转。担架以直线速度移动。两个齿轮的快轴表面是两个半径为1和2的圆柱表面。即时轴平面图II机架工具。凹面与对应的齿轮齿面触点或点接触，并且形成齿轮工作齿面或线或点的接触[5-7]。

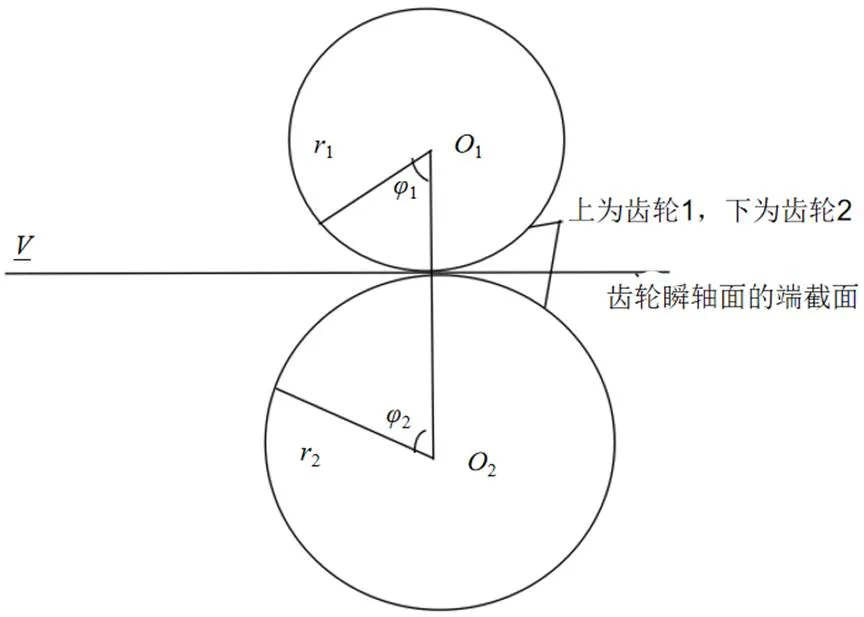
图1 齿轮齿面与刀具齿面

根据齿轮加工工具假想齿条的原理，根据法线面齿廓与端面齿廓之间的坐标变化关系，获得梁侧P数学模型。用于获得人造表面的数学模型，运动的相对位置关系如图2所示。

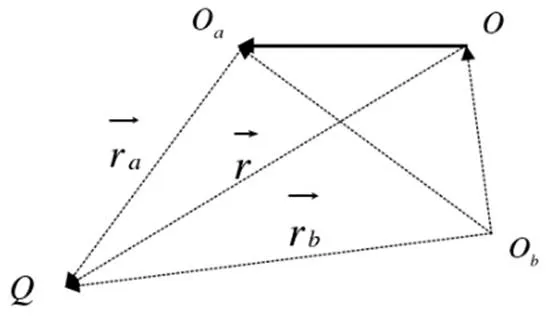
图2 相对运动矢量位置关系

由空间啮合原理可知，在空间运动过程中彼此啮合的齿条和人造齿表面在任何时候都接触。在某一点（接触点）切割，但是在这两种情况下，它们在净点处始终具有公共的接触平面，并且在净点处，牙齿两个表面的相对速度必须垂直于，仅以此方式确保两个牙齿表面可以在接触时不断滑动，他们既不会解放自己，也不会互相干扰[8-10]。

2 点线啮合动轮齿面数学模型机器模态分析

2.1 模型啮合齿轮间藕合关系的设定

在整个分析过程中，定义齿轮关系非常重要。所有参数模型和分析也比较复杂。因此，使用定义接触齿轮廓之间的节点连接关系的方法来模拟实际网格，以简化分析。为了实现此目标，需要使用ANSYS的APDL语言中的CE命令，以定义约束方程式来模拟齿轮。约束方程是使某些节点在特定方向上的位移满足某种关系，其公式如下：

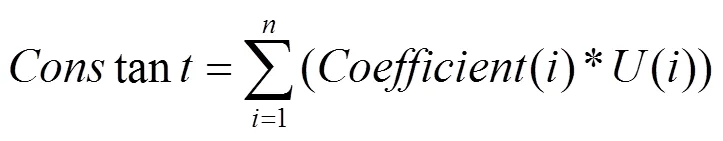
由改变齿轮啮合尺寸的原理可以知道，齿轮啮合方向是朝着两个齿轮基环间的内部公切线方向进行。因此，有必要根据基环的内部公共接触方向调整空间坐标系和节点坐标系以使其x或y方向一致，然后使用约束方程式调整节点坐标系，使网格节点在内部公共接触方向上具有相同的连通性，朝着某个方向前进。如图3所示，定义了齿轮与齿轮之间的联接关系，其中粗线的方向由周向位移确定。

将参数插入变量文件建立模型并安装于程序中。经过多次实验和比较，设定为当啮合线和不同齿轮之间的距离大于e-6时，两个节点认为是非接触的，否则为连续的。

2.2 点线啮合轮系的动力学模态分析求解

计算和分析方法以通过示例确认模型，表1中显示了点线啮合轮系的前10阶固有频率。完成表格计算后，可以打开后处理机器以监视结果并获取固有频率和相应的设置。由于空间限制，此处仅提取前10个固有频率，如表1所示。

表1 点线啮合轮系的前10阶固有频率

从自然频率分布表的前10个命令中可以看出，自然频率的第1阶为3050Hz，前10自然频率的第6阶分布在11000Hz和12000Hz之间。查看自然频率的一般分布，第1至第4自然频率，相应振动水平是具有不同振幅的三点线网轮的旋转振动。第5行的固有频率对应于网轮的虚线之一的振动模式，第6和第7命令是车轮的虚线网格的振荡设，第8至第10系列振动模式是对应于不同点线网格表面的振动模式。

2.3 点线啮合轮系中主要参数对模态的影响

对压力角以相同顺序变化时，分析其对整个齿轮系的影响。

在切线处，两齿轮轮廓曲线的共同法线（即齿廓的受力方向）与两齿圈的公切线（即点瞬时移动方向）所夹的锐角为压力角，也称为恒定角。对单个齿轮而言，为齿形角。正常齿轮的压力角通常为20°。较小压力角设备负载能力小于高压轮的负载能力，但在相同的运输重量下，轴承上的负载会增加，因此仅在特殊情况下才能使用。在ANSYS软件中，通过更改压力角参数进行形状分析，这里的压力角为18°, 20°, 22°。例如，表2和图4中显示了前10个固有频率。

表2 压力角分为18°, 20°, 22°的点线啮合轮系的前10阶固有频率

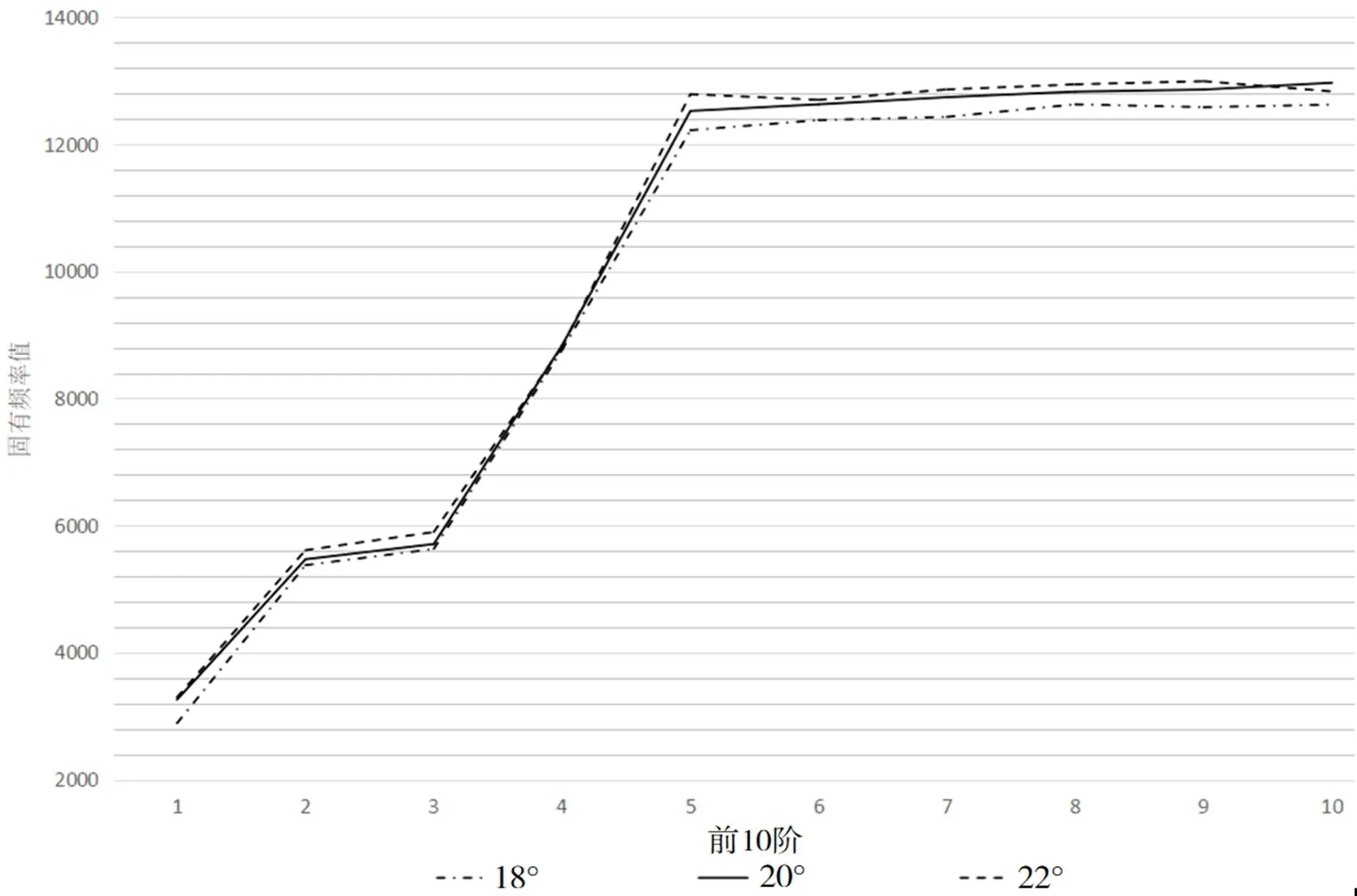
图4 压力角分为18°, 20°, 22°的固有频率分布图

可知，在同一压力角下，固有频率随着阶数增加而增大，而阶数一定，固有频率随着前10阶压力角的增大而增大。

3 结论

本文基于ANSYS的点线啮合齿轮理论，建立了点线齿轮的分析模型，分析阶数与固有频率关系，研究压力角和固有频率之间的变化过程，结果表明，阶数、固有频率以及压力角三者之间成正比关系。但有关最优化频率的确定，需要进一步分析计算。

[1] 郑朋，刘帅，李宽，等. 考虑内外啮合相位差的行星轮系动态特性分析[J]. 组合机床与自动化加工技术，2020(03): 16-21.

[2] 郭锐，赵之谦，贾鑫龙，等. 基于ANFIS的外啮合齿轮泵寿命预测研究[J]. 仪器仪表学报，2020, 41(01): 223-232.

[3] 田立勇，郑跃鹏，王慧. 基于自动化测控平台对外啮合齿轮泵的总效率研究[J]. 流体机械，2020, 48(02): 12-16.

[4] 马登秋，叶振环，魏永峭，等. 偏心激励下平行连杆加工的圆弧齿线圆柱齿轮啮合特性研究[J]. 机械传动，2020, 44(01): 7-12, 46.

[5] 古庭赟，杨骐嘉，林呈辉，等. 基于单机等值与选择模态分析的风电场等值建模方法[J]. 电力系统保护与控制，2020, 48(01): 102-111.

[6] 范宏权，徐彦，李晓东，等. 基于转角和啮合点关系的内啮合齿轮泵排量精确计算[J]. 液压与气动，2019(11): 125-129.

[7] 李大磊，李安民，张二亮. 一种齿轮时变啮合刚度的通用计算方法[J]. 重庆理工大学学报（自然科学），2019, 33(10): 61-66.

[8] 史雪林，肖文，干金鹏. 基于模态试验的碰撞传感器安装位置分析[J]. 重庆理工大学学报（自然科学），2015, 29(04): 24-28.

[9] 黄海，秦英奕，陶德馨，等. 点线啮合齿轮弯曲疲劳强度优化[J]. 机械传动，2012, 36(12): 60-63.

[10] HUANG H, QIN Y Y, TAO D X, et al. Multi-Objective optimization design of hard gear-face point-line meshing gear[J]. Applied Mechanics and Materials, 2019, 271-272: 1027-1031.

Research on dynamic modal analysis of point-line meshing gear based on finite element method

LUAN Kuo

(School of Mechanical Engineering, Wanjiang University of Technology, Anhui Maanshan 243031, China)

This article uses ANSYS's tooth profile and period changes of unexcited gears, and uses APDL language to establish a parametric modal analysis model of the dashed grid of the gear system. The APDL linear point grid analysis table is used to define a special interface, input parameters and automatically read, call the analyzer and perform dynamic difference calculation. By analyzing the relationship between the natural frequency and the order, the dynamic mode change process of the point-line meshing gear is reflected, as well as the influence process of the refraction between the pressure angle and the order on the mode. The development of this analysis program lays a strong foundation for the analysis and design ability of point line meshing gear mimicry.

ANSYS；APDL language；point-line meshing gear；modal analysis

2021-04-16

皖江工学院2019年度校级科研重点课题——基于MPC的半挂汽车路径跟随和侧向稳定性集成控制策略研究（WG19021ZD）

栾阔（1991-）男，安徽淮南人，助教，本科，主要从事机械工程研究，kexueyuandi100@163.com。

TH132.41

A

1007-984X(2022)01-0008-03