“互联网+”教育背景下网课学习效果评价的决策树建模

郭海兵 刘亚帅

摘要：在“互联网+”的教育背景下，由于线上学习的方式难以随时观察学生学习状况，因此如何有效地观测学生的网课学习效果是当前必须要研究的一个话题。本次研究以江西财经大学“计量经济学”课程为研究对象，主要通过Mooc学习平台后台和人为爬取两种方式来获取数据，运用ID3算法，以学习效率为因变量，计算各个属性的信息熵和信息增益，进行递归，进而出建立决策树模型，对学生的网课学习效果进行一个大致评价。

关键词：“互联网+”；MOOC在线学习平台；ID3算法；决策树

一、引言

在面临着疫情的突发情况，我国大多数大学生在家通过网络平台进行学习交流，近年来，在线教育平台得到了快速的发展，但如何评价学生在线学习效果的问题一直没有得到有效的解决。针对这个问题，本次研究学生利用网络平台进行学习时效果欠佳是由于观看视频过程中哪一个或者几个行为共同影响导致。

本次研究以江西财经大学计量经济学课程为研究对象，运用ID3算法，计算各属性的信息熵和信息增益，不断递归，寻找最优分割点，建立决策树模型，对学生的网课学习效果进行一个大致评价。

二、算法概述

决策树是一种常用的数据挖掘分类模型，呈树型结构，这是一种从机器学习领域中不断发展的用于分类的函数逼近方法，决策树模型具有计算速度快，结果容易解释，稳健性强的优点。ID3算法是决策树模型的基础算法之一，其基本思想是：通过分析属性的信息增益，找到最具有判别能力的划分属性，将样本划分为多个子集，每个子集按照类似的方法继续递归划分，最终得到决策树。ID3算法的核心问题就是如何判断出最优的划分属性，该算法运用属性分割前后的熵进行比较，计算信息增益，以此来度量属性的判别能力。相关计算公式如下：

（一）样本分类所需信息量

假设S是一个集合，包含有s个样本，有m个不同的类别属性值Ci，其中i=1，2，...，m。

给定了概率p1，p2，...，pm，其中，则对样本分类所需信息量为：

（1）

（二）樣本分类所需期望信息

假设属性A中有n个不同的取值，即a1，a2，...，an，根据属性A划分样本集S，分为n个不同的集合，即S1，S2，...，Sn，用sij代表样本集中属于sj的类别Ci的样本数，此时，样本量的计算公式为：

（2）

其中，表示第j个子集的权重。E（A）值越小，表示集合被划分得越彻底。

（三）信息增益

信息增益是指两个信息量之间的差距，计算公式如下：

（3）

计算每个属性的信息增益，然后进行比较，得到信息增益最大的属性，即具有最优判断能力的属性，选择该属性作为根节点，递归建立决策树，直至全部数据都属于同一类为止。

三、数据预处理

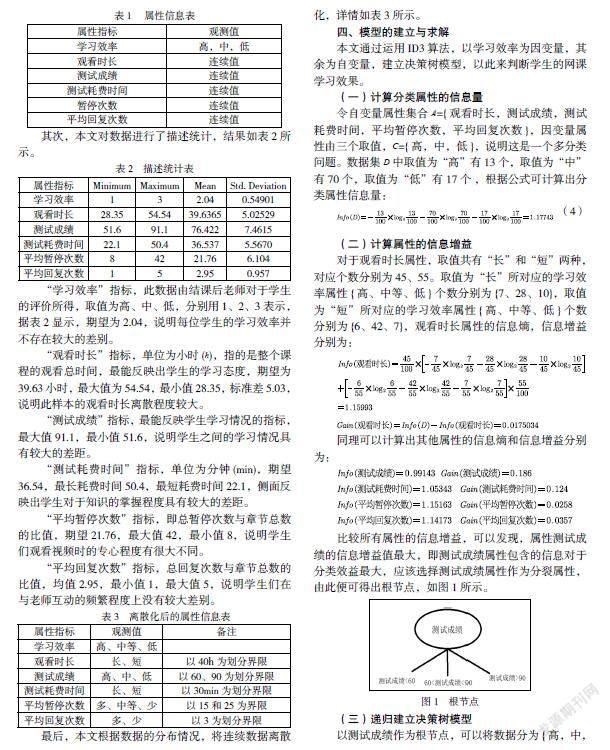
本次研究以江西财经大学的“计量经济学”课程为研究对象，课程共有13个章节，数据的获得途径主要是通过MOOC学习平台后台，也包括老师结课后对于学生的评价和数据爬取等途径。首先对数据进行了预处理，剔除掉了异常值，即课程只学习一半等异常情况，只统计完整学习并进行了课程测试的数据，收集到共100条数据，数据属性信息表如表1所示。

“学习效率”指标，此数据由结课后老师对于学生的评价所得，取值为高、中、低，分别用1、2、3表示，据表2显示，期望为2.04，说明每位学生的学习效率并不存在较大的差别。

“观看时长”指标，单位为小时（h），指的是整个课程的观看总时间，最能反映出学生的学习态度，期望为39.63小时，最大值为54.54，最小值28.35，标准差5.03，说明此样本的观看时长离散程度较大。

“测试成绩”指标，最能反映学生学习情况的指标，最大值91.1，最小值51.6，说明学生之间的学习情况具有较大的差距。

“测试耗费时间”指标，单位为分钟（min），期望36.54，最长耗费时间50.4，最短耗费时间22.1，侧面反映出学生对于知识的掌握程度具有较大的差距。

“平均暂停次数”指标，即总暂停次数与章节总数的比值，期望21.76，最大值42，最小值8，说明学生们观看视频时的专心程度有很大不同。

“平均回复次数”指标，总回复次数与章节总数的比值，均值2.95，最小值1，最大值5，说明学生们在与老师互动的频繁程度上没有较大差别。

最后，本文根据数据的分布情况，将连续数据离散化，详情如表3所示。

四、模型的建立与求解

本文通过运用ID3算法，以学习效率为因变量，其余为自变量，建立决策树模型，以此来判断学生的网课学习效果。

（一）计算分类属性的信息量

令自变量属性集合A={观看时长，测试成绩，测试耗费时间，平均暂停次数，平均回复次数}，因变量属性由三个取值，C={高，中，低}，说明这是一个多分类问题。数据集D中取值为“高”有13个，取值为“中”有70个，取值为“低”有17个 ，根据公式可计算出分类属性信息量：

（4）

（二）计算属性的信息增益

对于观看时长属性，取值共有“长”和“短”两种，对应个数分别为45、55。取值为“长”所对应的学习效率属性{高、中等、低}个数分别为{7、28、10}，取值为“短”所对应的学习效率属性{高、中等、低}个数分别为{6、42、7}，观看时长属性的信息熵，信息增益分别为：

同理可以计算出其他属性的信息熵和信息增益分别为：

比较所有属性的信息增益，可以发现，属性测试成绩的信息增益值最大，即测试成绩属性包含的信息对于分类效益最大，应该选择测试成绩属性作为分裂属性，由此便可得出根节点，如图1所示。

（三）递归建立决策树模型

以测试成绩作为根节点，可以将数据分为{高，中，低}三个子集，然后继续递归计算每个属性的信息熵和信息增益。

对于测试成绩为高的子集，即测试成绩>90的子集，对于学习效率属性{高、中、低}个数分别为{8，2，0}，按照递归的方式计算信息Info（测试成绩高）=0.42。

以此计算其他属性的信息熵和信息增益，即：

比较所有属性的信息增益，可以发现，属性观看时长的信息增益值最大，即观看时长属性包含的信息对于分类效益最大，应该选择观看时长属性作为分裂属性，由此便可得出根节点，如图2所示。

同理可得，对于测试成绩为中的子集，属性平均回复次数信息增益值最大，选其为根节点；对于测试成绩为低的子集，全部歸为一类，直接得到叶子节点。

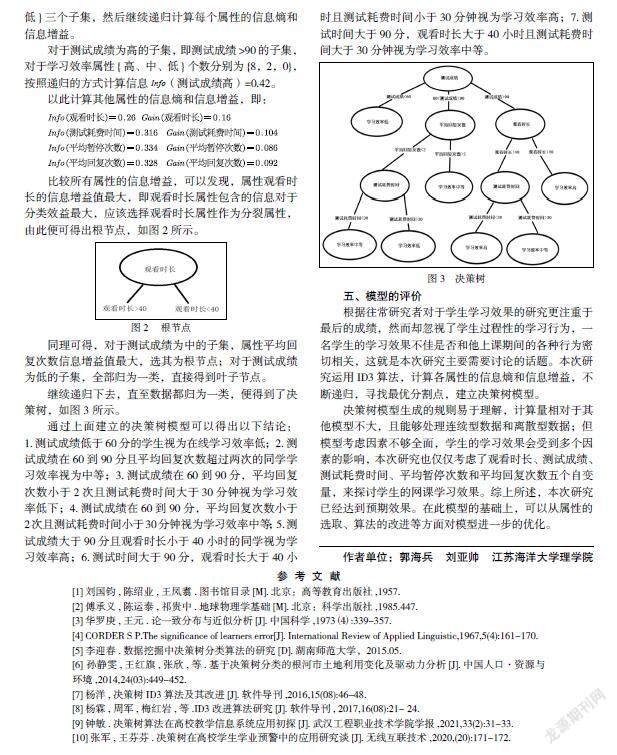
继续递归下去，直至数据都归为一类，便得到了决策树，如图3所示。

通过上面建立的决策树模型可以得出以下结论：1.测试成绩低于60分的学生视为在线学习效率低；2.测试成绩在60到90分且平均回复次数超过两次的同学学习效率视为中等；3.测试成绩在60到90分，平均回复次数小于2次且测试耗费时间大于30分钟视为学习效率低下；4.测试成绩在60到90分，平均回复次数小于2次且测试耗费时间小于30分钟视为学习效率中等；5.测试成绩大于90分且观看时长小于40小时的同学视为学习效率高；6.测试时间大于90分，观看时长大于40小时且测试耗费时间小于30分钟视为学习效率高；7.测试时间大于90分，观看时长大于40小时且测试耗费时间大于30分钟视为学习效率中等。

五、模型的评价

根据往常研究者对于学生学习效果的研究更注重于最后的成绩，然而却忽视了学生过程性的学习行为，一名学生的学习效果不佳是否和他上课期间的各种行为密切相关，这就是本次研究主要需要讨论的话题。本次研究运用ID3算法，计算各属性的信息熵和信息增益，不断递归，寻找最优分割点，建立决策树模型。

决策树模型生成的规则易于理解，计算量相对于其他模型不大，且能够处理连续型数据和离散型数据；但模型考虑因素不够全面，学生的学习效果会受到多个因素的影响，本次研究也仅仅考虑了观看时长、测试成绩、测试耗费时间、平均暂停次数和平均回复次数五个自变量，来探讨学生的网课学习效果。综上所述，本次研究已经达到预期效果。在此模型的基础上，可以从属性的选取、算法的改进等方面对模型进一步的优化。

作者单位：郭海兵    刘亚帅    江苏海洋大学理学院

参  考  文  献

[1] 刘国钧，陈绍业，王凤翥.图书馆目录[M].北京：高等教育出版社，1957.

[2] 傅承义，陈运泰，祁贵中.地球物理学基础[M].北京：科学出版社，1985.447.

[3] 华罗庚，王元.论一致分布与近似分析[J].中国科学，1973⑷：339-357.

[4] CORDER S P.The significance of learners error[J]. International Review of Applied Linguistic，1967，5（4）：161-170.

[5] 李迎春.数据挖掘中决策树分类算法的研究[D].湖南师范大学，2015.05.

[6] 孙静雯，王红旗，张欣，等.基于决策树分类的根河市土地利用变化及驱动力分析[J].中国人口·资源与环境，2014，24（03）：449-452.

[7] 杨洋，决策树ID3算法及其改进[J].软件导刊，2016，15（08）：46-48.

[8] 杨霖，周军，梅红岩，等.ID3改进算法研究[J].软件导刊， 2017，16（08）：21- 24.

[9] 钟敏.决策树算法在高校教学信息系统应用初探[J].武汉工程职业技术学院学报，2021，33（2）：31-33.

[10] 张军，王芬芬.决策树在高校学生学业预警中的应用研究谈[J].无线互联技术，2020，（20）：171-172.