Banach空间上的两个不动点定理的新证法

裴明鹤

(北华大学数学与统计学院，吉林 吉林 132013)

众所周知，Schauder不动点定理和Rothe不动点定理是非常著名的不动点定理，它们在常微分方程和偏微分方程的各种定解问题以及积分方程的可解性问题中有着非常广泛的应用.因此，受到微分方程学者的广泛关注.证明Schauder不动点定理的方法一般有3种：第一种如文献[1]，首先用有限秩算子(Schauder投影)逼近全连续算子，然后利用Brouwer不动点定理来得到；第二种如文献[2]，先证明Rothe不动点定理，然后利用全连续算子延拓定理来得到；第三种如文献[3]，先利用Dugundji延拓定理来得到闭凸集的收缩核性质，然后利用Rothe不动点定理来得到.纵观上述Schauder不动点定理和Rothe不动点定理的证明，不论哪种证法，事先都需要做一些较繁琐的准备工作.本文给出Banach空间上的Schauder不动点定理和Rothe不动点定理的新的比较简洁的独立的证法.本文的证法主要基于全连续算子的延拓定理连同Leray-Schauder度理论.

首先，为叙述方便引入一些记号，并简要介绍全连续算子的延拓定理连同Leray-Schauder度理论中一些熟知的结果.

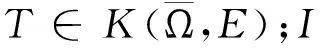
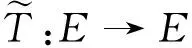
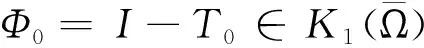
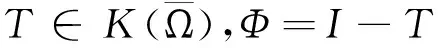
degLS(Φ，Ω，0)=degLS(Φ，Ω1，0).

有了以上准备，兹可以证明Banach空间上的Schauder不动点定理和Rothe不动点定理.首先，利用全连续算子延拓定理连同Leray-Schauder度的小扰动原理给出Schauder不动点定理的新证明.

定理1(Schauder不动点定理) 设D是实Banach空间E中的有界凸闭集，T：D→D是全连续算子，则T在D上至少有一个不动点.

(1)

(2)

又因为D是有界集，所以存在以原点为心、以r>0为半径的开球B(0，r)⊂E，使得D⊂B(0，r).记Ω=B(0，r).则由式(2)可得

注2在Schauder不动点定理中，关于空间E的条件可减弱为：E是实线性赋范空间.此时，代替全连续算子延拓定理，利用Dugundji延拓定理即可证明，详见文献[3].

其次，利用全连续算子延拓定理连同Leray-Schauder度的切除性和边界值性质，给出Rothe不动点定理的新证明.

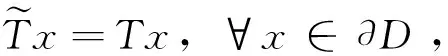
(3)

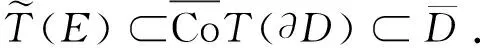
(4)

于是，由引理4可得

(5)

又由式(4)及Ω的选取知

于是，由引理2可得

此式连同式(5)隐含

更进一步，由式(3)和引理5，得到

注3定理1不能用定理2的证明方法来证明，这是因为在一般的Banach空间中的有界凸闭集D不一定有内点，从而即使T在D的边界上无不动点，但degLS(I-T，intD，0)仍可能无定义.