基于协整理论的淮河流域上游洪水预报实时校正方法

张旭旻，瞿思敏，李 倩，石 朋，嵇海祥，宋兰兰，王麒栋

(1.河海大学水文水资源学院，江苏 南京 210098； 2.苏州市网慧水利设计咨询有限公司，江苏 苏州 215128；3.水利部南京水利水文自动化研究所，江苏 南京 210008； 4.舟山市生态环境局，浙江 舟山 316021)

流域水文模型研究采用时不变非线性系统，通过历史水文数据对模型参数进行率定，用于未来洪水预报，但这种预报方案往往得不到令人满意的结果[1]。其原因在于，流域水文系统是一个时变非线性系统，在人类活动和气候变化的影响下，水文规律随时间变化。此外，流域水文系统是一个复杂系统，用模型进行模拟时，常进行一系列的假设和简化，这些假设和简化在外延时会带来较大误差。包红军等[2-4]通过构建模拟效果更准确的短时定量降水序列和洪水预报智能模型尝试解决模型外延时产生的误差问题。但在现有技术水平下，还无法从根源解决上述问题，因此，需要通过实时校正技术对预报结果进行适时、适量的校正，以提高洪水预报精度。

实时校正方法根据校正对象的不同大体上可以分为两类：一是过程误差校正方法(process bias correction，PBC)，二是终端误差校正方法(terminal bias correction，TBC)[5]。PBC主要对模型输入、参数、状态变量等进行校正，包括递推最小二乘校正法、卡尔曼滤波方法、动态系统响应曲线方法等。已有研究表明，动态系统响应曲线方法能够对模拟流量结果进行有效的校正[6-7]，但在实际应用中会出现“振荡”现象，可通过引入平稳矩阵减缓该缺陷。王莉莉等[8]构建了淮河中游的Preissmann四点隐式差分格式的一维水动力模型，并利用卡尔曼滤波对构建的水动力模型进行校正，结果表明，经过校正的模型对水位和流量的预报精度更高。TBC方法不考虑预报过程误差，直接对最终流量结果进行校正，从而达到实时更新原预报值的目的。TBC方法中自回归模型(autoregressive model，AR)应用最为广泛，该校正模型已被应用于多个流域的洪水预报结果实时校正中。已有研究表明，AR模型能够有效地对预报洪水结果进行实时校正，但对洪峰流量误差校正效果不佳[5,9-11]。其原因在于，AR模型存在一个基本假定，认为误差序列存在序贯相关性[12]，当这种序贯相关性因为序列突变而变化时，会导致较差的校正结果，而洪峰前后误差序列不可避免地存在突变，所以AR模型校正效果较差。同时AR模型需满足时间序列为平稳序列的前提条件，而实际上，大多数水文要素时间序列都是非平稳的。基于非平稳时间序列运用AR模型进行分析会导致“伪回归”现象的发生。

Engle等[13]1987年提出的协整理论为非平稳时间序列分析提供了有力的理论依据，常被用来处理同阶单整的非平稳时间序列问题[14-15]。基于协整理论的误差修正模型(error correction model，ECM)通过引入一阶差分项消除了变量可能存在的趋势因素，避免了“伪回归”问题，同时通过引入误差修正项削弱了序贯相关性的影响。ECM模型作为计量经济学中解决误差修正问题的经典模型，在水文学中应用较少。针对河川径流为平稳系列的假设所造成的“伪回归”问题，张利亚等[14,16-17]分别将ECM模型应用于第二松花江流域、黄河流域和渭河流域，构建了年径流量预测模型，取得了较好的应用效果。

已有研究表明，分布式水文模型能够较好地考虑流域降水与下垫面空间分布不均的特点，有效提高洪水预报精度[18-19]，同时垂向混合产流模型综合考虑了蓄满、超渗产流模式，因此，在半干旱半湿润地区具有良好的应用效果。本文采用分布式垂向混合产流模型模拟结果作为本次实时校正算法研究的数据来源。本文以淮河流域上游为研究区域，尝试将协整理论与ECM模型应用于自回归建模中，解决AR模型无法分析非平稳时间序列以及序贯相关性的问题，并在分布式垂向混合产流模型基础上，建立一阶至三阶AR模型、ECM模型、基于误差修正的自回归模型(autoregressive error correction model, ARECM)对模拟结果进行校正，对比各模型校正效果，以期提高淮河流域上游洪水预报精度，为防洪调度提供更有力的科学依据。

1 研究区概况与数据来源

淮河流域地处我国东部，介于长江与黄河流域之间，流域面积18.7万km2。本文以淮河鲁台子以上流域为研究区域，面积为8.86万km2，气温由北向南升高，蒸发量南小北大，年平均蒸散发为900～1 500 mm。淮河流域为典型半干旱半湿润流域，多年平均降水量为911 mm，多年平均径流深为231 mm，多年平均径流系数为0.25，其径流年内分布不均，主要集中在汛期。流域水系如图1所示。研究数据来源于水文年鉴(2003—2014年)逐日逐时段实测降水、流量和蒸散发数据(逐时段蒸散发数据由逐日数据平均得到)。

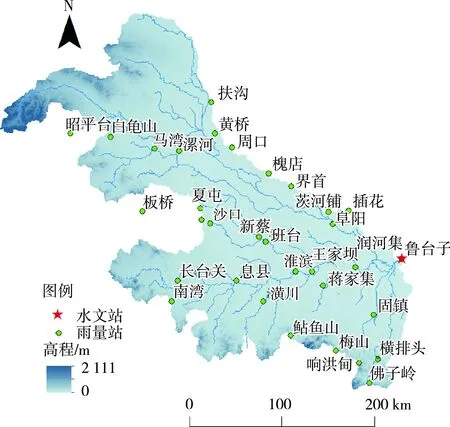
图1 鲁台子以上流域水系与站点Fig.1 Schematic diagram of water system and stations in river basin above Lutaizi station

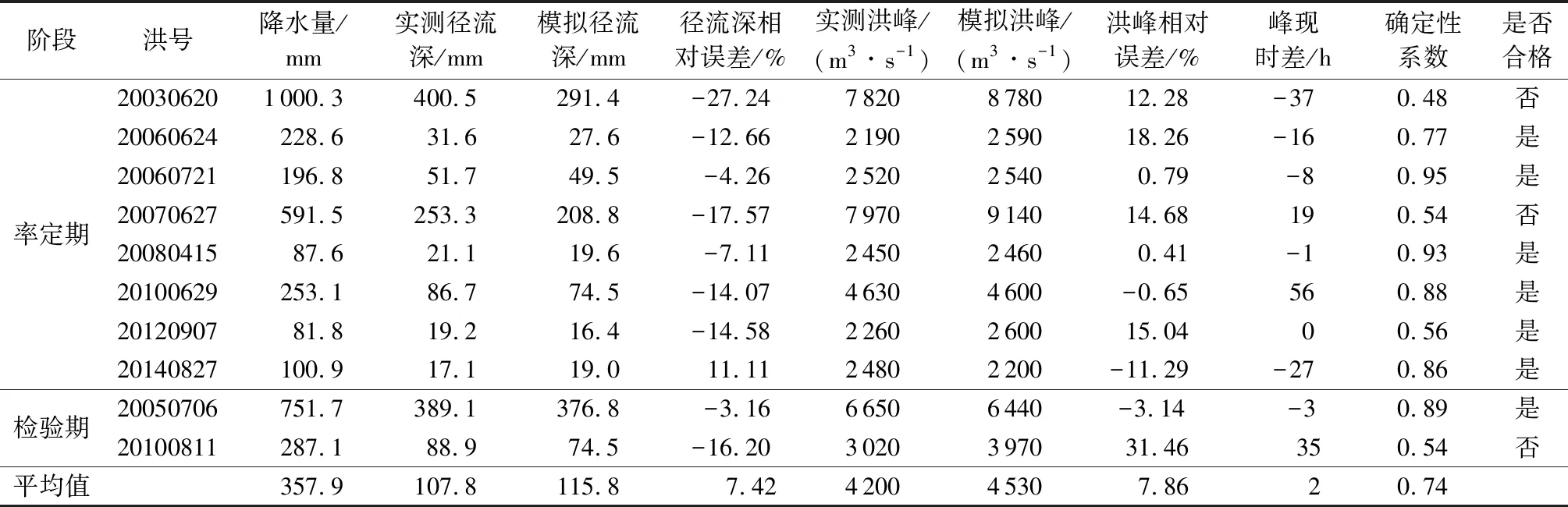
表1 鲁台子以上流域洪水模拟结果Table 1 Results of flood simulation in river basin above Lutaizi station

2 分布式垂向混合产流模型构建

垂向混合产流模型由包为民等[20]于1997年提出，模型将超渗产流与蓄满产流进行垂向组合，降水到达地面后，首先通过下渗能力分布曲线划分为地面径流和下渗水流。在土壤缺水量大的区域，下渗水流补充土壤含水量，不产流；在缺水量小的区域，下渗水流补充土壤含水量达到饱和后，产生地面以下径流。由于同时考虑了超渗和蓄满两种产流模式，该模型既适用于湿润地区产汇流过程模拟，也适用于半干旱半湿润地区产汇流过程模拟[20-21]。为了更好地考虑降水和下垫面分布不均对流域产汇流过程的影响，本文基于垂向混合产流模型和DEM资料，构建了栅格型分布式垂向混合产流模型，根据2003—2014年淮河鲁台子站实测资料，选取10场洪水对模型进行参数率定与检验，模型模拟结果如表1所示。结果表明，模型平均确定性系数为 0.74，模拟结果合格率为70%，能够较好地模拟淮河流域上游洪水过程。

3 实时校正方法

3.1 ECM模型

ECM模型是一种具有特定形式的计量经济学模型。首先需要对自变量x与因变量y进行协整分析，以发现变量之间的协整关系(即长期均衡关系)，假设协整关系的回归方程形式为

yt=b0+b1xt+εt

(1)

式中：b0、b1为系数；εt为t时刻误差修正项，即回归方程的残差序列，反映t时刻因变量在短期波动中偏离长期均衡关系的程度。

将误差修正项看作一个解释变量，连同其他反映短期波动的解释变量一起，建立短期模型，即ECM模型。误差修正模型的主要形式为

Δyt=b0+b1Δxt+γεt-1+μt

(2)

式中：Δyt、Δxt为t时刻因变量与自变量的一阶差分；εt-1为t-1时刻误差修正项；μt为纯随机数列；γ为系数，多为负值。

根据实际应用的场景，可对ECM模型的形式进行变化，首先将观测流量作为因变量，模拟流量的一阶滞后项作为自变量进行协整分析，得到

Qobs,t=b0+b1Qsim,t-1+εt

(3)

式中：Qobs,t为t时刻实测流量；Qsim,t-1为t-1时刻模拟流量。

基于式(3)构建的短期模型为

ΔQ′obs,t=b0+b1ΔQsim,t-1+γεt-1+μt

(4)

其中

εt-1=Qobs,t-1-b0-b1Qsim,t-2

式中：ΔQ′obs,t为估计的t时刻实测流量数据一阶差分；ΔQsim,t-1为t-1时刻模拟流量数据一阶差分。

假设具有t时刻的实测流量数据以及t+1、…、t+n时刻的预报流量数据，在利用ECM模型对预报数据进行滚动校正时，首先计算出ΔQsim,t与εt，根据式(4)计算得出ΔQ′obs,t+1，将ΔQ′obs,t+1与Qobs,t相加即可得到t+1时刻校正后流量结果Q′obs,t+1；类似地，对t+n+1时刻预报数据进行校正时，根据ΔQsim,t+n与εt+n计算得出ΔQ′obs,t+n+1，将ΔQ′obs,t+n+1与Q′obs,t+n相加即可得到t+n+1时刻校正后流量结果Q′obs,t+n+1。因此，假设分布式垂向混合产流模型预见期为n，则ECM模型预见期为n+1。式(4)为一阶ECM模型，二阶ECM模型如式(5)所示，三阶模型形式相似。

ΔQ′obs,t=b0+b1ΔQsim,t-1+b2ΔQsim,t-2+γεt-1+μt

(5)

式中b2为系数。

3.2 AR模型

AR模型基于变量的自相关性，认为t时刻变量的值可以用其之前各时刻的值来预测。在实时校正过程中，根据实测流量与预报流量计算误差序列，在假设误差序列为平稳序列的前提下，建立误差AR模型，估计下一时刻误差值，从而达到校正效果。AR模型为

(6)

式中:et为t时刻预报值与实测值之间误差；ak为系数；k为自回归阶数；ε′t为t时刻随机误差，为零均值独立同分布误差序列。

3.3 ARECM模型

依据Granger表述定理，如果变量x与y是协整的，则变量间的短期非均衡关系总能由ECM模型表述[13]。为便于解释推导，假设根据实测流量与预报流量构建的误差序列存在如下一阶自回归形式的长期均衡关系：

et=α0+α1et-1+εt

(7)

式中α0、α1为系数。

实际上，单场洪水误差序列很少处在均衡点上，因此根据单场洪水建立的误差AR模型只能反映误差序列的短期或非均衡关系。假设针对单场洪水具有如下二阶自回归形式模拟方程：

et=β0+β1et-1+β2et-2+μt

(8)

式中β0、β1、β2为系数。该模型显示，t时刻误差值et可由et-1和et-2估计得到。由于误差序列可能是非平稳的，因此不能直接应用普通最小二乘法(ordinary least square，OLS)计算参数取值。根据式(8)可得

Δet=β0+β1et-1-et-1+β2et-2+μt

(9)

对式(9)进一步变换后可得

Δet=β1Δet-1-λ(et-1-γ0-γ1et-2)+μt

(10)

其中

γ0=β0/λγ1=(β1+β2)/λ

式中λ为系数。如果et为一阶单整序列，则Δet为平稳序列，可以应用OLS法计算模型参数取值。令γ0=α0，γ1=α1，由式(10)可得：

Δet=β1Δet-1-λεt-1+μt

(11)

式(11)通过引入一阶差分项消除了变量可能存在的趋势因素，避免了“伪回归”与可能存在的多重共线性问题，解决了非平稳误差序列的自回归建模问题，同时通过引入误差修正项，体现了变量水平值信息。式(11)为本文采用的一阶ARECM模型，式(12)为二阶ARECM模型，三阶模型形式相似。

Δet=β1Δet-1+β2Δet-2-λεt-1+μt

(12)

3.4 评价指标

选取修正效果评价系数[1]与确定性系数作为评价校正效果优劣的指标。并根据GB/T 22482—2008《水文情报预报规范》，针对洪峰与径流量分别选取洪峰相对误差、峰现时差、径流深相对误差对洪水要素校正效果进行详细的评价。

修正效果评价系数为

(13)

式中Qraw,t为校正后t时刻流量。

4 实时校正模型应用效果分析

4.1 平稳性检验

采用广泛应用于时间序列平稳性检验的Augment Dickey-Fuller (ADF)检验法对10场洪水误差系列进行平稳性检验。基于ADF检验的回归方程为

(14)

式中：α、β、δ为系数；p为总滞后阶数；ζt为白噪声序列；ξi为滞后阶数为i的线性时间趋势项。

对淮河流域上游10场洪水的误差序列进行ADF检验，结果如表2所示。10场洪水中除20120907与20140827次洪水误差序列外，其余洪水误差序列均为平稳序列。本研究中，为了体现ARECM模型在非平稳时间序列建模中的优势，对20120907与 20140827次洪水依旧构建AR模型，对垂向混合产流模型模拟结果进行校正。需要强调的是，针对20120907与20140827次洪水构建的AR模型为“伪回归”模型，并没有实用价值。

表2 ADF检验结果Table 2 Results of ADF test

4.2 协整检验

协整关系能够反映变量间长期存在的一种稳定均衡关系。对多变量应用ECM模型时需满足变量间具有协整关系的前提条件，因此，对变量进行协整检验是很有必要的。协整检验[13]核心在于对回归方程残差进行单位根检验(即平稳性检验)，若残差序列为单整序列(即平稳序列)，则变量间存在协整关系。本文对误差修正模型中的变量进行协整检验，各变量间协整检验结果的P值如表3所示。当P>0.05时，认为在5%置信度区间内接受原假设；当P>0.1时，认为在10%置信度区间内接受原假设，而原假设为不具有协整关系。

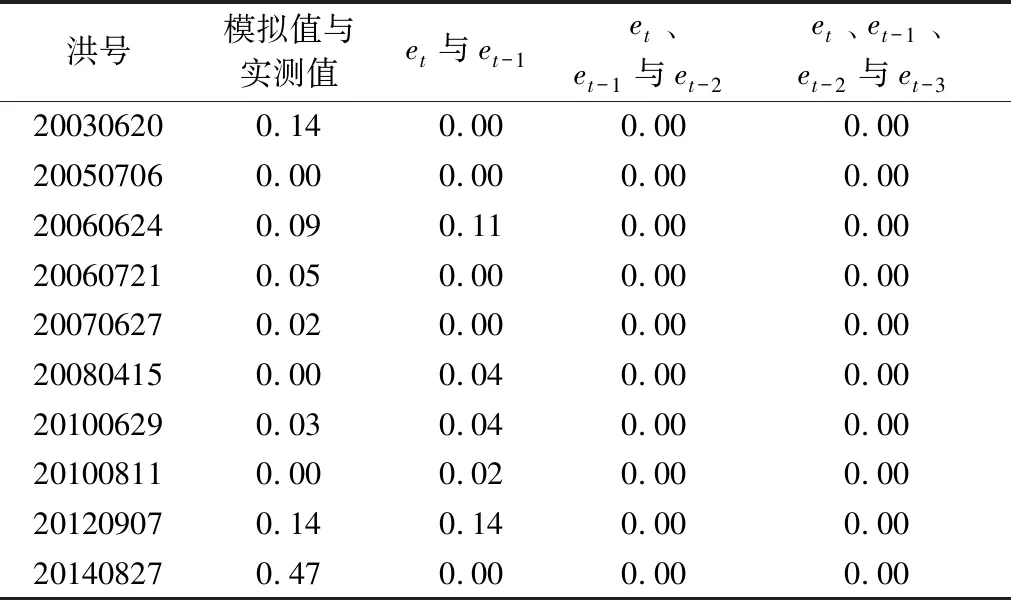
表3 协整检验结果的P值Table 3 P values of cointegration test results

在建立ECM模型的10场洪水中，对模型模拟值与实测值进行协整检验，其中7场洪水P值小于0.1，在10%置信度区间内拒绝原假设，认为序列间具有协整关系，通过了协整检验。未通过10%置信度协整检验的3场洪水中，有2场洪水P值为 0.14，可以近似认为通过了协整检验；而20140827次洪水，P值为0.47，未通过10%置信度协整检验，因此，不采用ECM模型对该场洪水进行误差校正。在一阶ARECM模型建立中，对et与et-1进行协整检验，10场洪水中有8场洪水通过了5%置信度协整检验，其中，未通过协整检验的2场洪水的P值分别为0.11与0.14，可以近似认为通过10%置信度协整检验，能够用于模型建立。针对二阶与三阶ARECM模型，所有变量在各场次洪水中均通过了5%置信度的协整检验，可用于建立ARECM模型。

4.3 模型效果分析

选取流域2003—2014年10场洪水资料以及分布式垂向混合产流模型模拟结果，分别建立一阶至三阶AR、ECM和ARECM实时校正模型对模拟结果进行校正，并对校正效果进行对比分析。

从校正结果的修正效果评价系数(表4)看，ECM与ARECM模型相较于AR模型具有明显优势，3种方法的校正效果与模型阶数基本成正比，但针对某一场洪水，建议依照最小信息量准则确定校正模型的阶数。AR、ECM、ARECM模型平均修正效果评价系数为-0.77、0.76、0.98。AR模型表现效果较差，原因在于20120907与20140827次洪水误差序列不满足平稳序列的假设，校正效果较差，删除以上两场洪水后，AR模型的平均修正效果评价系数提高到0.20。针对20120907与20140827次洪水，ARECM模型修正效果评价系数明显优于AR模型，其中ARECM模型修正效果评价系数分别达到了1.00与0.92远高于AR模型的-9.15与-0.65(一阶至三阶模型的平均值)，证明了ARECM模型在针对非平稳误差序列建模方面具有很强的能力，同时证明了可以通过引入协整理论解决AR模型无法针对非平稳误差序列建模的问题。根据确定性系数的统计结果(表5)，ARECM模型校正效果明显优于ECM模型与AR模型，且ECM模型校正效果优于AR模型，证明了ECM与ARECM模型在实时校正方面的适用性。

由表6可见，以洪峰相对误差为评价指标，AR模型校正效果最差，ECM模型与ARECM模型校正后的洪峰相对误差相较于AR模型分别减小了11.22%与17.41%。其原因在于ARECM模型通过引入误差修正项，保证了变量的水平值没有被忽视，减弱了误差序列的序贯相关性对建模的影响，使得模型在洪峰处不仅依靠误差序列的自相关性进行校正，同时也考虑了校正后误差序列与实测误差序列上一时刻的偏离程度，避免了AR模型在误差突变点处产生较大误差的现象。峰现时差(表7)与洪峰相对误差结果相似，ARECM模型与ECM模型校正效果远优于AR模型，其中，20120907与20140827次洪水不满足平稳序列假设，但仍构建了AR模型，导致校正效果较差，因此没有在表7中计算这两场洪水二、三阶AR模型校正后的峰现时差。由表8可见，以径流深相对误差为评价指标，ECM模型与AR模型对模拟结果的校正效果相近，不如ARECM模型。

表4 修正效果评价系数统计结果Table 4 Statistics of correction effect evaluation coefficient

表5 确定性系数统计结果Table 5 Statistics of deterministic coefficient

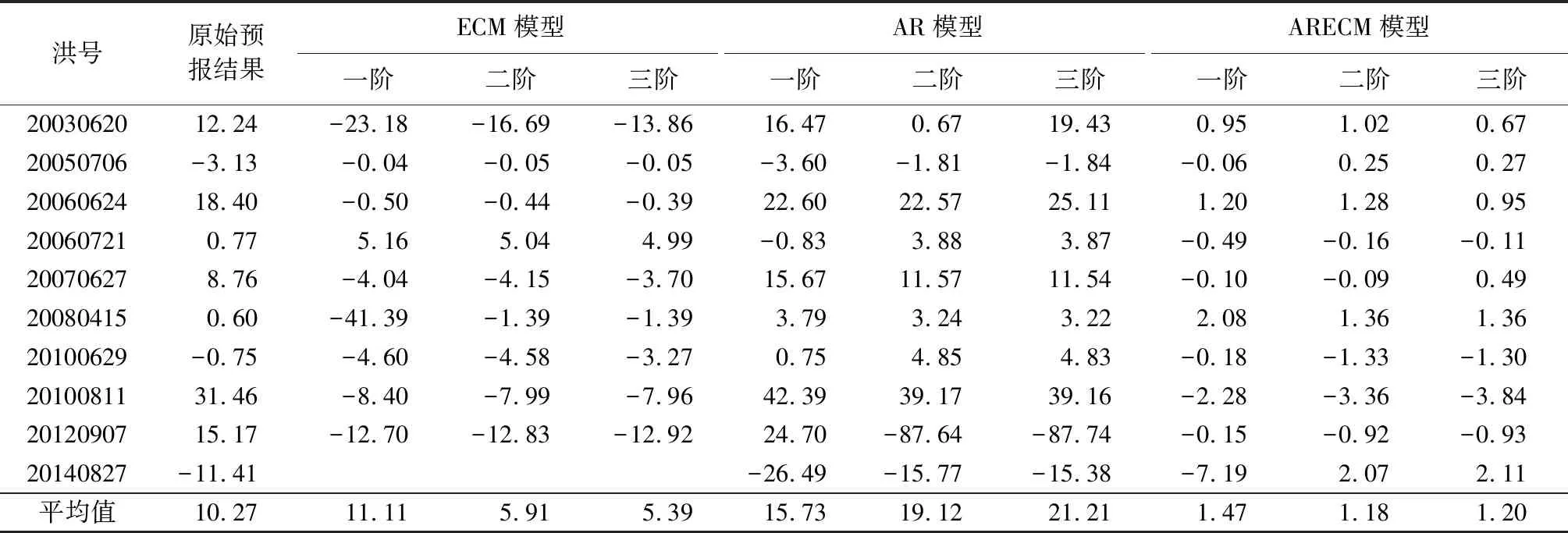
表6 洪峰相对误差统计结果 单位：%Table 6 Statistics of relative error of flood peaks unit: %

综上所述，AR模型校正效果最差，其主要原因在于AR模型以误差序列的自相关性为基础进行校正，无法对洪峰处误差进行较好的校正；ECM模型依赖实测值与预报值，因此在洪峰处模型校正效果较好，但径流深方面，校正效果与AR模型相似。ARECM模型模拟效果较好，通过误差修正项的引入，避免了AR模型在洪峰处校正效果差的缺陷，提高了洪峰误差校正效果，同时通过引入协整理论解决了AR模型无法对非平稳序列建模的问题。

为了直观地展示校正效果，选取2场典型洪水(20030620和20100811次洪水)，对比3种三阶实时校正模型校正后的流量过程线(图2)。从图2可以看出，2场洪水的流量模拟与实测结果相差较大；AR模型以实测与模拟流量的误差序列为基础进行校正，对模拟流量线型影响较小；ECM模型直接考虑实测流量的影响，能够显著改变模拟流量线型，使校正结果更贴近实测流量；ARECM模型校正效果最好，能够对模拟洪峰流量进行准确的校正，显著提高了淮河流域上游洪水预报精度。

表7 峰现时差统计结果 单位：hTable 7 Statistics of error of time to flood peaks unit: h

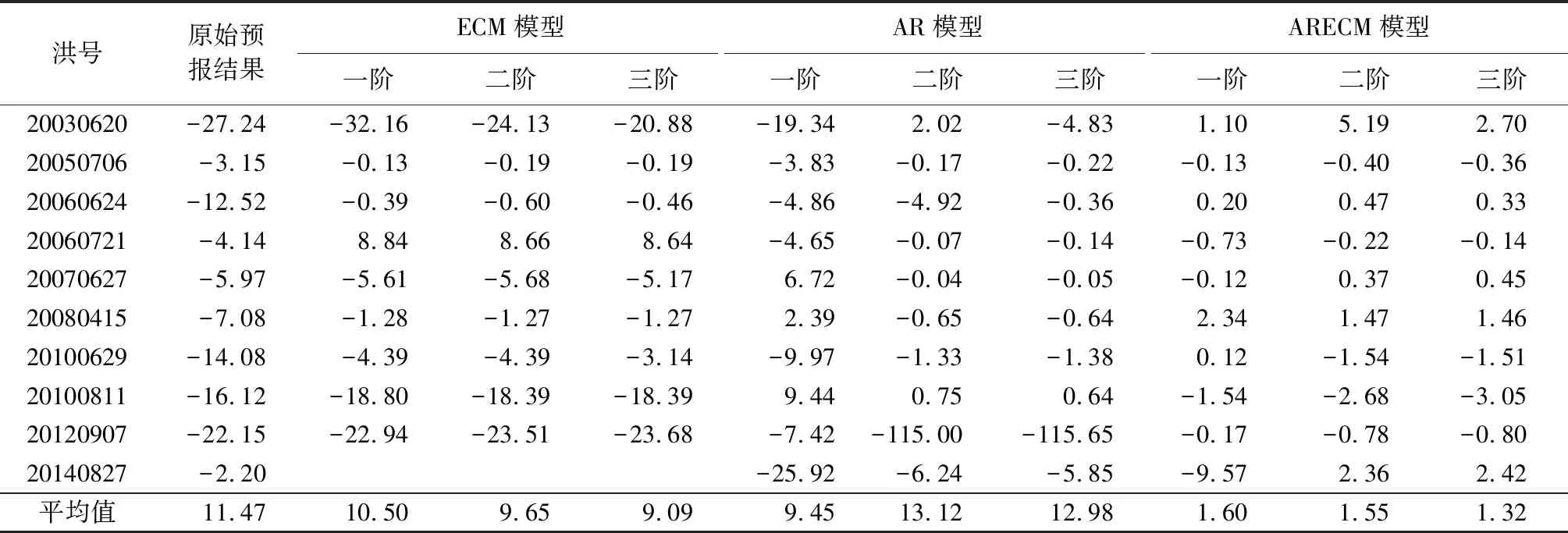
表8 径流深相对误差统计结果 单位：%Table 8 Statistics of relative error of runoff depth unit: %

(a) 20030620次洪水

5 结 论

a.AR模型能够有效地对垂向混合产流模型洪水模拟结果进行校正，但由于序贯相关性的影响，在洪峰处校正效果较差，而在径流深方面与ECM模型校正效果相似。

b.ECM模型能够较好地解决洪水实时校正问题，模型校正效果优于AR模型但劣于ARECM模型，从洪峰相对误差角度，校正效果相较于AR模型改善了11.22%。

c.ARECM模型通过引入误差修正项，减弱了误差序列序贯相关性对建模的影响，并通过引入一阶差分项，避免了“伪回归”与可能存在的多重共线性问题，避免了AR模型对洪峰校正效果较差的缺陷。模型校正后平均洪峰相对误差为1.28%，平均径流深相对误差为1.49%，从洪峰相对误差角度看，ARECM模型校正效果相较于AR模型改善了17.41%，校正效果较好，可用于校正实时洪水预报结果。