巧处理“阅读与思考”环节 真落实文化育人功能*——以“勾股定理”教学为例

⦿安徽省淮北市淮北师范大学数学科学学院 雷红艳

⦿安徽省合肥市合肥师范学院附属西安路学校 喻 悦

《义务教育数学课程标准(2022版)》(简称课标)在2022年4月22日正式颁布，课标指出：“在教材内容编写时，要注重教材创新，就要拓展视野，如教材中介绍数学文化、数学发展前沿等，内容设计要反映数学在自然与社会中的应用，展现数学发展史中伟大数学家，特别是中国古代与现代著名数学家，以及他们的数学成果在人类文明发展中的作用，增强学生的爱国情怀和民族自豪感”[1].为此，“阅读与思考”等成为各版本教材不可或缺的栏目.

在实际教学过程中，“阅读与思考”等类似栏目的设置初衷并没有得到有效落实，主要原因包括不少教师忽视栏目价值、缺少应用指导等.为有效落实数学文化的育人功能，本文中以人教版“勾股定理”教学设计为例，分析了HPM视角下“阅读与思考”在情境创设、新知探究、新知应用和课后拓展等不同环节的四种处理方式.

1 人教版教材中“阅读与思考”的统计分析

“阅读与思考”栏目是人教版初中数学教材凸显数学文化育人的特色栏目.笔者对人教版教材涉及到数学史素材的“阅读与思考”进行了统计:共26个“ 阅读与思考”栏目，涉及数学史素材的有12个，占比将近一半.数与代数中包括：从算术发展到代数历史；《九章算术》中的“正负术”；方程的起源与发展；《九章算术》比例算法；引发第一次数学危机；《九章算术》中的“方程术”；勾股定理的三种证明方法；托勒密《天文学大成》.图形与几何中包括：几何学的起源；金字塔《画法几何》；《周脾算经》径一周三、刘徽“割圆术”.

这表明，作为落实数学文化综合育人价值的重要载体，数学史素材是“阅读与思考”栏目的重要组成内容.这些素材是教材编写者集体智慧的结晶.教师不应轻易脱离教材去重新选择其他素材，应深入研究这些素材，以达到综合育人的价值与实现途径.对此栏目教师可以有效改进教学，激发学生的学习兴趣，感受古人智慧的魅力，养成民族自豪感.

2 HPM视角下的四种处理方式

汪晓勤[2]提出了将数学史融入数学教学的四种方式——附加式、复制式、顺应式和重构式.

“勾股定理”位于人教版八年级下册第17章，包含“勾股定理的证明”“费马大定理”两个“阅读与思考”栏目.在上述四种处理方式的指导下，以“勾股定理”教学为例，本文中分别展现“勾股定理的证明”在情境创设、新知探究、新知应用和课后拓展等教学环节的四种创新应用.

2.1 附加式——巧用数学故事，创设问题情境

“情境创设”是数学教学的起始环节.适当的情境式(以数学故事、历史事件、生活情境等)导入，学生更能投入到问题情境中，为新知探究做好铺垫.但是，对于问题情境的有效创设，不少教师出现平铺直叙和一味追求创新性两种极端，导致情境与学生认知、兴趣并不匹配，反而令教学效果大打折扣.在教学实践中，合适的数学故事蕴含丰富的数学文化信息，有利于学生更好地体会故事中的数学知识内涵，升华学生的情感态度以及价值观念.

在“勾股定理”教学伊始，教师可将“勾股定理的证明”加工成蕴含丰富中国元素的数学故事，创设问题情境，激发学生对数学历史故事的兴趣并引发数学思考.

师：若未来技术可以实现黑洞穿越，我们回到西周开国时期的朝堂上，同学们可以听到周公与商高讨论勾股测量的对话.来看一段据《周髀算经》记载的对话视频.展示视频内容[3](以动画展示)：

(周公知商高精通数学，谦虚询问其如何测定“日高”和“地宽” ，商高答道：“数之法出于圆方，圆出于方，方出于矩，矩出于九九八十一.故折矩，以为句 (同勾)广三，股修四，径隅五.既方之，外半其一矩，环而共盘，得成三四五.两矩共长二十有五，是谓积矩”.)展示故事中的“勾广三，股修四，径隅五”的图形(图1、图2和图3).

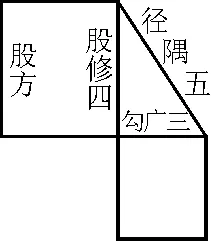
图1 既方之

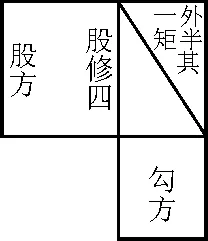
图2 外半其一炬

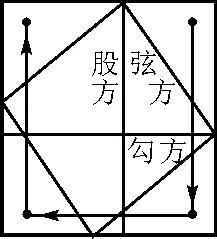
图3 环而共盘

师：同学们，视频中有哪些数学知识点呢？

生1：在测量“日高”时，提到句 (同勾)广三，股修四，径隅五，这是刻画某个图形的关系量.

师：生1提到的视频中的勾广三，股修四，径隅五，其实，这是我们今天要学习的新知识——勾股定理.什么是勾股定理呢？又如何证明它呢？

全班学生陷入了思考……

设计意图：首先，教师以情境导入数学故事，并用多媒体展示其内容，从教学起始就抓住学生的感知，激发学生的学习兴趣，启发学生进一步思考.其次，以问题驱动的形式“提取”视频中的关键内容，精准定位学生要学习的目标与任务.

2.2 重构式——巧设驱动问题，引导新知探究

“探究新知”是数学教学的核心环节.一个好的探究过程是学生高效掌握知识、实现深度学习的基本保障.探究过程的科学设计，既需要分析教材与学情，注重数学知识的逻辑线与学生的认知线的统一，还需要注意认知负荷理论的运用，不能给与学生过多的额外认知负担.

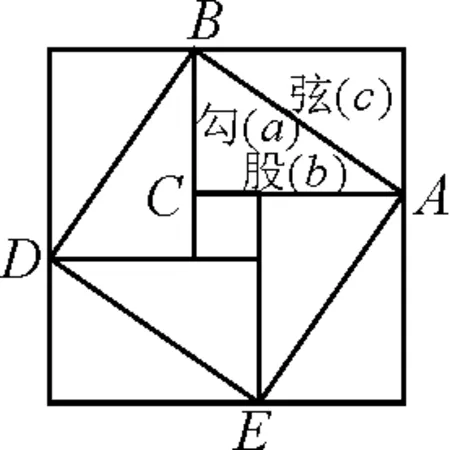
图4

在“勾股定理证明”的教学过程中，证明思路的自然获得是教学难点，不少教师选择赵爽弦图(图 4).该方法涉及到的基本图形数量、拼图情况都较多，给学生的探究与发现带来较大困难.以人教版“阅读与思考”中勾股定理的第三种证明方法——美国第20任总统詹姆斯·加菲尔德的证法为素材，笔者对其进行重构，改进了传统的探究过程.

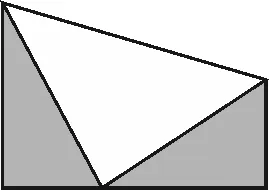
图5 拼接图

师：同学们，你们能用手中的两个全等三角形来证明刚刚的猜想吗？

(学生利用课前准备的两个相同的直角三角形分组尝试不同的拼接方法，得到如图5所示的图形.)

师追问：图5中的白色三角形的面积与两个阴影直角三角形的面积之和之间有什么关系[3]？

生2：我认为白色三角形的面积等于两个阴影直角三角形的面积之和.(其他学生肯定生2的回答.)

师：为什么呢？

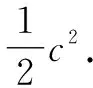
师：生3详细地展示了证明过程，但最后的结果并不是面积相等，而是得到了c2=a2+b2，即直角三角形的两条直角边的平方和等于斜边的平方，即得到并证明了勾股定理.

设计意图：课前让学生准备教具(2个相同的直角三角形)，引发学生探究数学内容的积极性和好奇心.利用两个相同三角形拼接的方法，既符合数学实验教学模式，还降低了学生的认知负担，提高了教学效益.同时，学生经历了完整的“问题—猜想—证明”的过程，有效提升了合情推理与演绎推理素养.

2.3 顺应式——巧设活动支架，体会数学精神

“新知应用”是促进学生对新知的深入理解和检验学生掌握知识的重要环节.例题和练习题的有效设置与变式是传统教学的优势.在这里，紧跟“新知探究”环节，可以继续运用数学史素材，在新知应用中融入数学故事，让学生亲身体会数学故事所蕴含的精神.

师：刚才已经证明了勾股定理.如果已知一个直角三角形的两条直角边长分别为7 cm和12 cm，那么斜边的长度是多少？(题目较简单，多数同学可知.)

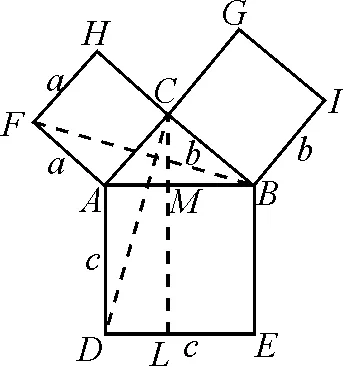
图6

师：接下来，请同学们思考如下问题.三个边长分别为a，b，c的正方形，拼接为如右图6所示的图形，其中∠C=90°.连接BF，CD，过点C作CL⊥DE，交AB于点M，交DE于点L，连接CL.证明正方形ADEB的面积等于正方形AFHC与正方形BIGC的面积之和.

全班学生再次陷入深思……

题目难度稍大，学生不能直接想到解题思路.教师适时引导学生观察图中三个正方形的位置和数量关系，寻找合适的支架，将上面两个正方形和下面的正方形进行联结，思考是否可以利用三角形的性质来研究正方形的性质.

学生分组讨论之后，派代表回答，由此证明了结论a2+b2=c2，得出勾股定理.

设计意图：勾股定理的发现导致无理数的诞生，产生了第一次数学危机,《几何原本》记载了西方毕达哥拉斯对勾股定理的证明.利用数学史中有趣且真实的数学故事，融入新知应用的课堂中，学生更能从中领会数学精神，感受教学背后的数学史价值.同时，由易到难、层层推进的练习，使学生能熟练掌握新知，激发起学生更高知识水平的求知欲.

2.4 复制式——巧设拓展项目，提升文化修养

“课后拓展”是检验教师教学效果、拓展学生核心素养的重要途径.从古至今，勾股定理不仅应用广泛，最重要的是它贴近人们的实际生活，因此对它的证明从未停止探索.新的证法不断出现，其证明方法至今已有500余种.由此，教师可拓展课后学习项目，布置拓展项目作业：查阅相关资料，探究勾股定理的证明方法(至少两种).通过在教室设置“勾股定理展览区”、勾股定理证明方法微视频或PPT、讲故事等方式进行展示汇报.

设计意图:通过拓展项目作业的完成过程，学生可以跨越时空，与古代数学家隔空“对话”，从中感受数学史带来的文化冲击，激发数学学习兴趣，了解数学史背后蕴含的价值，培养良好的资料检索、表达交流等能力.

3 结语

著名数学史家李文林[4]曾提出“为教育而历史”.数学史融入数学教育，具有深刻的教育价值.基于教材“阅读与思考”中的“勾股定理”一节内容，以数学史作为辅助教学工具，形象展示了数学知识形成的背景以及发展过程.笔者以“勾股定理”中融入数学史的四种方式，巧妙地处理“阅读与思考”环节并进行教学设计，激发学生的学习兴趣和探究新知的好奇心、体会数学精神、提升数学修养，真正地落实数学文化育人功能；同时，还可提高教师的数学素养，其内在专业知识结构也能不断得到更新和丰富；对数学课程也具有一定的实用价值，一些优秀案例可为数学课程增添教学素材，实现其教学价值.一线教师切不可忽视教材中的“阅读与思考”栏目，合理运用并将其中的数学史融入教学中，是当代教师课堂教学研究的重中之重.