龙潭过江通道北锚碇基坑开挖稳定性数值模拟研究

杜丽辉，王少卿

（苏交科集团股份有限公司，江苏 南京 211112）

0 引言

过江通道的打通，为相邻两地的商贸往来带来了巨大的便利，但随之也导致了基坑开挖等土建工程难题。为此，许多研究人员对地连墙或基坑开挖稳定性进行了研究分析[1-3]。吴坤铭[4]采用有限元法对拉锚地连墙支护深基坑进行开挖过程的稳定性分析及优化设计。吴忠等[5]结合新沟河延伸拓浚工程，基于ABAQUS有限元软件，评价扶壁间距对T形地下连续墙稳定性的影响。肖安斌等[6]结合白洋长江公路大桥北岸锚碇深基坑边坡工程实际，利用理论分析和FLAC3D有限差分法基本原理，得到了深基坑边坡工程岩体动态变形及稳定性演化规律。由于工程地质条件不同，数值分析结果往往存在巨大差异，为此，本文采用FLAC3D软件对龙潭过江通道工程北锚碇地连墙及基坑开挖施工过程进行了数值模拟分析，研究不平衡荷载工况下不同施工步骤土体、地连墙、内衬的位移以及地连墙与内衬的内力响应情况，为同类工程施工提供参考。

1 工程概况

1.1 地理情况

仪征至禄口机场高速公路（仪禄高速）拟利用龙潭过江通道规划线位过江。通道位于长江南京段与镇扬段分界处，距离上游南京长江四桥约16.8km，距离规划七乡河通道9.8km，距离下游润扬大桥约28.6km。项目地理位置如图1所示。

1.2 北锚碇基坑支护设计情况

北锚碇采用圆形基础，圆形基础外径为75m，基础埋深22m，持力层为弱胶结含砾砂岩，地连墙深33m，嵌固深度11m。基础前侧设置26个隔舱，高度11.5m。基础采用外径72m，壁厚1.5m的圆形地连墙基础加环向钢筋混凝土内衬支护结构。为防止地下连续墙底脚发生渗流及踢脚破坏，有利于增加基坑的抗隆起稳定性，地下连续墙嵌岩不少于2m。基坑开挖采用逆作法施工。为保证地连墙开挖阶段受力及刚度的需要，在地下连续墙顶部设置刚度较大的帽梁。帽梁为钢筋混凝土环形结构，地连墙顶部伸入帽梁10cm，顶部竖向钢筋全部伸入帽梁，与帽梁相连。帽梁悬出地连墙外侧1m，悬出内侧1.5m。帽梁总宽度4.0m，高2.5m。内衬及土体分层施工，基础顶面以下0～7m深度内衬厚1.5m，分层施工高度为（3+2+2）m；7～13m深度内衬厚2.0m，分层施工高度为（3+3）m；13～22.5m深度内衬厚2.5m，分层施工高度为（3+3+3.5）m。内衬施工层高取2m、3m和3.5m。各层内衬底面设置为11.3°的斜坡。

为防止内衬施工出现裂纹及收缩变形，每层内衬混凝土分15段进行施工，每段浇筑长度为14.451m，上下层接头错开2m，在一个单元长度内设置长2.8m的微膨胀混凝土后浇段。北锚碇地连墙基坑如图2所示。

2 北锚碇开挖施工有限元模型

2.1 有限元模型建立

考虑边界效应影响范围的情况下将模型尺寸长×宽×高为400m×400m×200m。根据需要将此处网格大小设置为2m，模型边缘处的网格大小为10m，中间部分网格缓慢增大。模型单元网格均为六面体网格单元。如图3所示为本次模型三维数值模型图。本次模拟中土体采用实体单元进行模拟。地下连续墙及内衬采用结构单元进行模拟。图4为地下连续墙与内衬的连接示意图。

2.2 参数选取及边界条件

各材料的物理力学参数主要依据岩土工程勘察报告，模型各项材料的物理力学参数如表1所示。模型左右边界约束水平方向的位移，底部边界约束竖向位移，地表为自然边界，所有自由度均不约束，渗流边界采用不透水边界条件。在基坑开挖后的内边界上，固定节点孔压为0，模拟基坑内部的实际流体边界状态。在模型顶部施加20kPa的力，模拟地表的超载作用。基坑在开挖过程中，由于受到地层结构、开挖顺序和已有建筑等现场条件的影响，基坑两侧可能受到不同大小荷载的作用。根据设计资料，本次在地连墙一侧25m范围内施加向下30kPa荷载作为不平衡荷载进行计算。

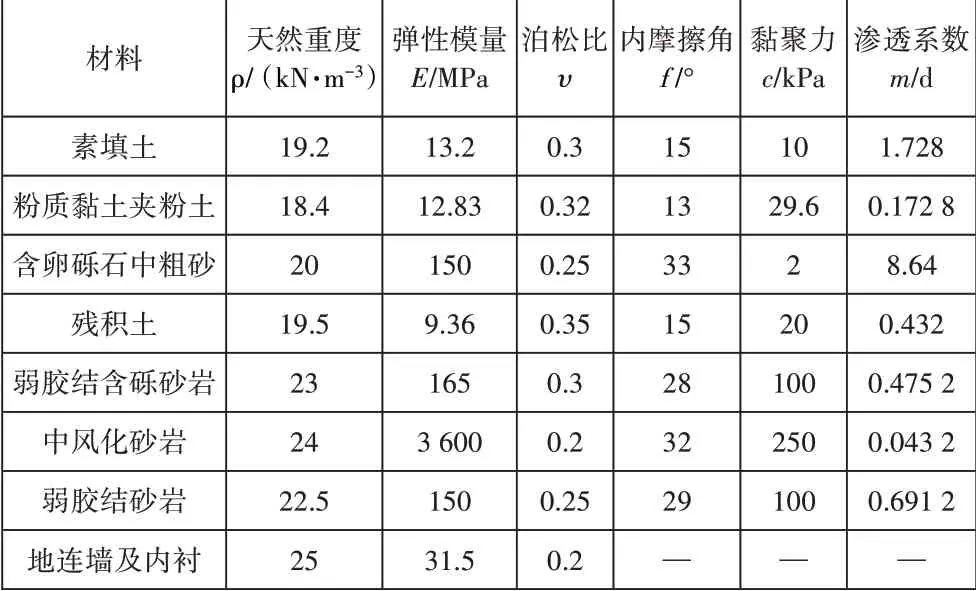
表1 地层与支护结构计算采用力学参数表

3 数值计算结果分析

3.1 北锚碇地连墙及基坑开挖位移影响分析

不同施工步骤土体及结构最大位移趋势曲线如图5所示。

随着施工的进行，土体的位移、地连墙的位移以及混凝土内衬结构的位移整体呈现增大趋势。其中土体最大位移值出现在基坑底部。基坑开挖到第七层及第八层时，土体、地连墙及内衬结构位移和内力变化明显。其中地连墙的最大弯矩出现在弱胶结含砾砂岩与中风化砂岩交界位置处；地连墙轴力随着深度的增大而增大，在底部达到最大；地连墙最大剪力也出现在地连墙底部，并且在弱胶结含砾砂岩与中风化砂岩地层范围内变化较大。土体位移的最值一直出现在基坑底部，表现出隆起的趋势。地连墙位移最大值出现在残积土地层处。考虑不平衡荷载时，基坑底部的隆起现象变化不大，但不平衡荷载作用的位置土体表现出更大的沉降，而地连墙另一侧土体发生隆起。同时地连墙及其内衬结构在偏载侧的位移更大。

计算结果的最不利工况为：基坑开挖第七层及开挖第八层土；地连墙结构的最不利位置为距地连墙顶端约4/5位置处，对应地层为弱胶结含砾砂岩及中风化砂岩交界位置，内衬内力最大位置出现在内衬第六层范围，内衬第六层对应地层为残积土，物理力学性质较差，施工到该步骤时，应加强在该位置的监控量测。

3.2 北锚碇地连墙及基坑开挖内力分析

不同施工步骤结构内力最大值趋势曲线如图6所示。

由图6可知，地连墙及内衬的内力值随着施工的进行而增大。第八层土开挖并施加内衬后，各个结构的内力达到最大值。其中，地连墙的最大弯矩出现在弱胶结含砾砂岩与中风化砂岩交界位置处，其值为1 789.40kN·m；地连墙轴力随着深度的增大而增大，在底部达到最大，其值为3 983.8kN；地连墙最大剪力也出现在地连墙底部，其最大值为672.60kN，并且在弱胶结含砾砂岩与中风化砂岩地层范围内变化较大；内衬的最大弯矩为91.37kN·m；内衬的最大轴力为220.67kN；内衬的最大剪力为63.56kN。内衬内力的最值出现在层与层的交界位置处。将内衬内力与地连墙内力进行对比，内衬内力的最大值分别为相应地连墙内力最大值的5.11%、5.41%、9.45%。不平衡荷载工况与普通工况相比，内力大小及分布情况相差不大，内衬结构承担的内力较小，并未充分发挥其承载能力，更多的作用是作为结构的安全储备，增加结构的安全系数。不平衡荷载对结构偏压侧及非偏压的内力影响很小，并且随着开挖深度的增加逐渐减少至可以忽略不计。

4 结论

本文采用FLAC3D软件对龙潭过江通道工程北锚碇地连墙及基坑开挖施工过程进行了数值模拟分析，得到的主要结论如下：

（1）随着施工的进行，土体、地连墙、内衬的位移逐渐增大。土体最大位移值出现在基坑底部，基坑出现较为明显的隆起现象。内衬结构的内力响应明显小于地连墙。内衬结构承担的内力较小，并未充分发挥其承载能力，更多的作用是作为结构的安全储备，增加结构的安全系数。

（2）计算结果的最不利工况为基坑开挖第七层及开挖第八层土；地连墙结构的最不利位置为距地连墙顶端约4/5位置处，对应地层为弱胶结含砾砂岩及中风化砂岩交界位置，内衬内力最大位置出现在内衬第六层范围，内衬第六层对应地层为残积土，物理力学性质较差，施工到该步骤时，应加强在该位置的监控量测。