高速公路路基压实质量PFWD检测指标统计学分析

许忠印

（河北雄安京德高速公路有限公司，河北 保定 071700）

0 引言

在高速公路路基的施工过程中，对路基压实质量进行控制是保证路基具有足够的强度和刚度的重要技术措施[1]。但如果路基压实出现过度压实或压实度不足的现象，路基将会出现沉降问题，这就会使路面产生不平整现象[2]。目前对于路基压实均匀性方面的研究较少，不足以满足工程实际要求。本文基于统计学原理分析对比一般路基段、台背和路桥过渡段三种路基形式的路基压实均匀性状态，对路基压实均匀性检测指标的分布状态、离散程度和集中趋势进行研究。

1 现场试验

1.1 现场试验概述

选取京德高速公路K24+400—K24+600处一般路基段作为试验段，利用便携式落锤弯沉仪PFWD对试验段进行检测。以弯沉值和回弹模量作为路基压实质量单点检测指标，利用统计学基本原理分析检测指标的分布状态、离散程度和集中趋势，达到判断路基压实质量以及探究路基压实均匀性分布规律和变化规律的目的。

京德高速公路路基横向宽度34.5m，为双向六车道高速公路，沿路基横断面压实层每隔3m作为一个检测点位，检测11个点；对于一般路基段沿路基纵向30m每3m作为一个检测点位，检测10个点。测点总数为110个。检测时应保证检测路段碾压完成，最好在各结构层碾压完成后封闭交通，第二天进行检测。

1.2 检测数据预处理

1.2.1 产生异常值的原因

在高速公路路基施工过程中，利用便携式落锤弯沉仪PFWD进行路基压实均匀性检测时会受到施工质量、测量员操作以及气候等因素的影响，导致检测指标数据存在异常值。且为了检测数据的准确性，在一个检测点处测得多个数据。一般情况下，统计学中的异常值是指在个别检测点位出现的某些特别大或特别小的可疑值，在路基压实施工过程中，碾压完成后利用便携式落锤弯沉仪和土壤模量刚度仪GeoGauge对路基进行检测，路基压实检测值的准确性是压实检测过程中的最基本要求，异常检测值将会对统计分析过程产生影响。

在进行波动性分析过程中，若没有将异常数据点进行筛选、剔除，波动性分析图上就会出现突变点，即波动曲线的突然上升或下降。异常值不能反映路基的实际压实质量，如果将异常值点纳入波动性分析图中，会导致压实均匀性不合格，在路基施工完成后异常值会对路基压实均匀性的评价结果造成影响。且压实检测异常值将会导致压实质量的目标值不准确，影响目标值的大小，从而影响整个区域的统计分析参数，导致不能准确判定路基压实程度、稳定性、均匀性等[3]。

1.2.2 异常值处理方法

由于产生异常值的原因众多，在进行路基压实均匀性检测时难免会存在明显偏离其余数值的点位。路基压实均匀性检测过程中异常值产生的原因有：①试验段路基填料的参数会对路基压实均匀性产生影响；②试验段坡度较大时，在碾压过程中出现部分区域压实程度不足或者过度压实；③不同的测量员操作得到的检测数据存在差异。

在进行路基压实均匀性分析前，需要对检测数据进行异常值的筛选和剔除。为了保证试验数据的准确性，本文采用单样本t检验法对检测数据进行处理[4]。根据样本均值对单个样本进行估计，即利用样本均值去估计总体均值。

1.2.3 检测指标的异常值处理

弯沉值分布图见图1，回弹模量分布图见图2。图中分别给出了一般路基段上路堤顶部弯沉值和回弹模量110个检测点位的分布状态，由于路基填料自身的变异性以及施工等的影响，可以看出整个碾压面检测指标值在某一区间内波动，但有部分点位数值波动较大。因此，压实检测数据均有离群值，需对其进行异常值处理。依照传统的异常值分析方法，认为检测数据产生突变较大的点为异常值点，但由于整个碾压面上的压实数据存在不同程度的波动，传统方法可能将压实薄弱或过度压实区域的数据判定为异常值，造成有效数据的丢失。

本文通过单样本t检验对检测指标的异常值进行处理，确定试验段检测指标的目标值范围；将异常值逐个剔除。利用箱型图进行检测指标数据异常值的筛选。表1为单样本t检验的结果。

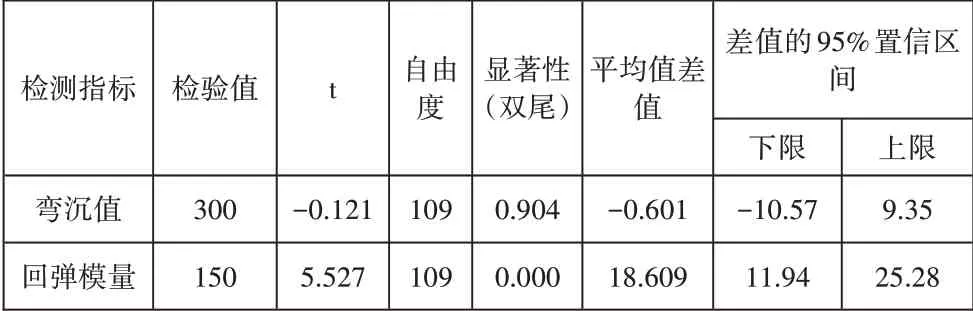
表1 单样本t检验结果表

单样本t检验结果见表1，可以看出，t统计量的观测值是由样本均值与原假设检验值的差除以表1中的标准误差平均值后得到的。检测指标的检验值和总体均值的95%的置信区间分别为(-10.57,9.35)，(11.94,25.28)，分别加上检验值即可得到总体均值的95%置信区间分别为(289.43,309.35)，(161.94,175.28)。即有95%的把握认为弯沉值均值在289.43～309.35之间，检验值300包含在置信区间内。有95%的把握认为回弹模量均值在161.94～175.28之间，检验值150没有包含在置信区间内。试验段检测指标的均值均在样本均值置信区间内。

利用箱型图进行检测指标数据异常值的筛选。箱型图的箱体和上下两条线以内的部分代表了一个试验段除去奇异值和极端值以外的所有检测指标值。奇异值和极端值分别为超过箱型图整体代表的指标值的1.5倍和3倍的检测指标值，处理前弯沉值箱型图见图3，处理前回弹模量箱型图见图4。

表2为异常值处理前后检测指标数据的统计分布状况，分析可得，在应用单样本t检验进行异常值处理后，弯沉值数据中异常值和奇异值的比例占总体数据的比例较大，压实均匀性检测数据的均值和标准差都受到影响；回弹模量数据中异常值和奇异值的比例占总体数据的比例较小，对压实均匀性检测数据的均值的影响较小，但对标准差和变异系数的影响较大，以上分析表明，异常值和奇异值的存在对路基压实质量评价的影响较小。

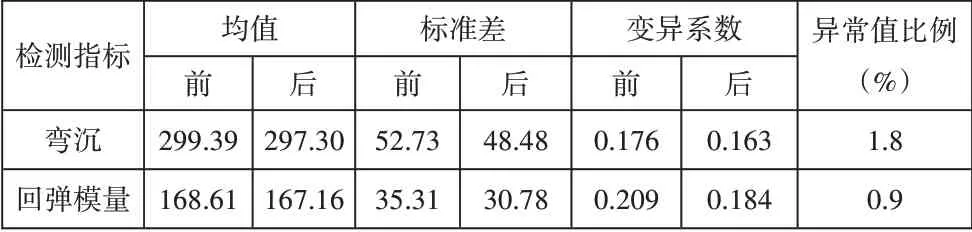
表2 异常值处理前后检测数据的统计结果对比

因此，在利用单点检测指标进行路基压实均匀性评价时，路基压实检测指标异常值和奇异值的存在对压实均匀性的评价与控制影响较大。进行路基压实均匀性检测与评价时有必要进行异常值筛选与处理。

2 路基压实均匀性分析

2.1 分布状态分析

弯沉值频率见图5，回弹模量频率见图6，分别表示试验段检测指标的频率分析结果。对整个试验段的路基压实均匀性检测数据在异常值处理前后的分布形态可以发现，就压实均匀性评价而言，少量的异常值会导致本来正态分布的压实检测数据产生偏态分布，可以看出，利用PFWD测得的单点检测指标数据基本服从正态分布规律，图中纵轴为频数，各条形块显示了各检测值区间的频数。通过对检测指标数据进行频数分析和GUSS拟合得到频率分布直方图，图5中拟合系数均大于0.8，说明检测数据的分布与正态分布逼近效果较好[4]，即单点检测指标数据集中分布在均值附近，且在均值两侧均匀变化，变化趋势基本相同。

表3为检测指标的偏度系数和峰度系数表，反映了实测数据的分布形态和分布特征。数据的分布形态主要指分布对称性、偏斜程度和陡缓程度。偏度系数绝对值越大，表示数据分布形态的偏斜程度越大，峰度系数绝对值越小，表明数据分布与标准正态分布的陡缓程度越相近。

表3 检测指标的偏度系数和峰度系数

2.2 离散程度分析

表4为标准差和变异系数表。对试验段实测数据进行描述性统计分析，得到检测指标数据的标准差和变异系数[6]。标准差和变异系数代表数据值分布离散程度的描述性统计量，其中标准差是代表变量取值距均值的平均离散程度，变异系数是样本标准差与均值的比值。

表4 检测指标的标准差和变异系数

标准差和变异系数越大，路基压实质量越不均匀，检测指标数据越趋于离散。由表4可以看出弯沉值与回弹模量的标准差相差较大，但变异系数较为接近。其主要原因是弯沉值的实测目标值比回弹模量大。因此，试验段弯沉值和回弹模量的目标值离散程度几乎相同。

2.3 集中趋势分析

表5为检测指标的均值和均值标准误差表。对试验段实测数据进行描述性统计分析，得到检测指标数据的均值和均值标准误差。均值和均值标准误差是代表数据值分布集中趋势的描述性统计量。样本均值代表检测数据的集中趋势，统计学中将数据视为来自总体的一个随机样本，均值标准误差越大，表明整个试验段检测数据均值与总体均值平均偏差程度越大，从而检测数据的集中趋势越差。

表5 检测指标的均值和均值标准误差

综上所述，路基压实质量检测指标的分布状态、离散程度和集中趋势均可以从不同方面反映路基的压实质量以及路基整体压实均匀性程度。从各描述性统计指标来看，弯沉值和回弹模量代表了相同的路基压实均匀性状态。

3 结语

本文基于统计学原理，采用单样本t检验法对路基压实质量检测指标的异常值进行了处理，通过对单点检测指标进行统计学分析初步分析了路基压实质量和路基压实均匀程度。结果表明：

（1）单样本t检验法可以很好地对检测指标数据的异常值进行筛选和剔除，异常值的存在会对路基压实质量目标值以及路基压实均匀性的评价造成影响。

（2）路基压实检测指标的分布状态、离散程度和集中趋势可以集中反映路基的压实均匀性状态。

（3）路基压实质量检测指标数据频率分析的拟合系数均大于0.8，基本服从正态分布，即检测指标值集中分布在均值两侧，变化范围较小。