运用化归思想求函数最值的策略*
黑龙江省佳木斯市第一中学 孔祥文
黑龙江省佳木斯大学 方海文
在教学过程中,教师应尊重教育规律,努力把学生培养为学习的主人,使学生的学习真正发生.但是教师要问自己:教室里大多数的学生,学习真的发生了吗?有的教师无视学生的自主学习动机,剥夺学生做事情的权利,省略与学生的有效对话,抑制学生探索的欲望.为了学生的长远发展,教师应该把课堂学习的主动权还给学生,课堂应该充满更真实的对话、认真的意见和真正的引导,展示“真正的学习”是什么样子的.
1 运用化归思想解决问题的一般模式及基本观点
在问题解决的过程中,将待解问题不断变形、转化,直至把它归结为已经解决的或容易解决的问题,最终得到原问题的解答.这就是化归思想[1].
1.1 运用化归思想实现问题解决的一般模式
化归思想一般模式如图1所示.

图1
1.2 基本观点
(1)运动与变化的观点
事物不是静止的,它是在不断地变化着的.解决数学问题时,把静止变成运动,把常量变成变量,利用运动与变化的方法解决问题.
(2)联系与转化的观点
事物不是独立存在的,是相互联系并能够转化的.在解决数学问题时,要不断地找出问题之间的联系和转化的方法,来解决数学中的问题.
(3)优选化归的观点
一般的数学问题可以分为两种,一种是创造新方法解决问题,一种是与以前所学的知识相结合共同来解决问题.同时,后一种方法在实际中最常用,并且在解决问题中常常利用化归的方法.所以,在面对数学问题时,我们通常优先考虑化归方法[2].
2 运用化归思想求解函数最值的策略
2.1 等价转化法求最值
两个命题A和B,若A⟺B,则称A与B逻辑等价.等价转化法是把待解命题A通过某种方法转化与其同真同假的等价命题B,通过转换的方法解决命题B得出结果,就意味着解决了命题A的问题.
例1已知抛物线y2=4(x-1),试在这个抛物线上找一点P,使点P到焦点与到点(4,1)的距离之和最小.
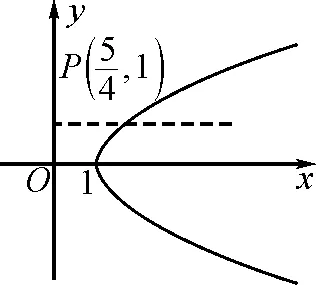
图2
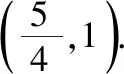
2.2 数与形的转化求最值
通过数与形之间的转化,不仅可以把数量关系的问题转变成图形分析的问题,还可以利用图形关系的分析,在图中直接看出变量之间的关系,从而解决问题,节省时间,开发思维能力.
数与形之间的转换,通常有以下几种情形:(1)实数与数轴上的点的对应关系;(2)函数与图象的对应关系;(3)曲线与方程的对应关系;(4)以几何元素和几何条件为背景,建立起来的概念;(5)所给的等式或代数式的结构含有明显的几何意义.
(1)用数与形的转化解平面几何的最值问题
平面几何中与三角形、圆等有关的问题,可以利用建立坐标系的方法,把图形问题转化为代数式的运算问题来解决.

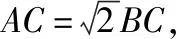
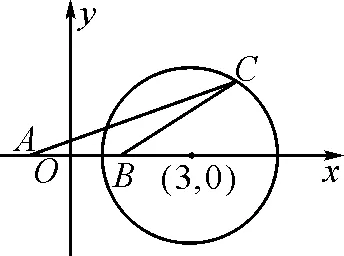
图3

化简,得
(x-3)2+y2=8(y≠0).
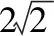
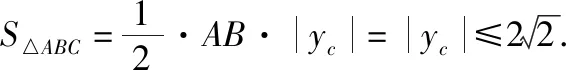

(2)用数与形的转化解圆锥曲线问题
解析几何中求代数式的最值问题常常可以联系代数式中各量的的几何意义,转化为斜率、截距、距离等模型去解决.与圆锥曲线有关的最值问题,合理应用圆锥曲线的定义是解决此类问题的有效途径.
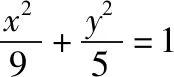


图4
由椭圆定义,可知|PF1|=2a-|PF2|=6-|PF2|.
所以 |PF1|+|PA|
=6-|PF2|+|PA|
=6+|PA|-|PF2|.
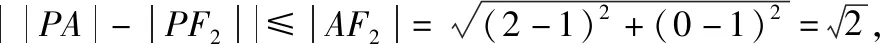
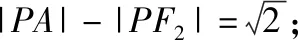
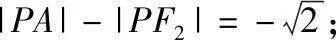

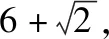
2.3 利用基本不等式化归转化求最值
利用不等式求最值主要是指运用基本不等式或它的一些变形式求代数式的最值.这种方法主要适用于和为定值或积为定值(或可转化为和或积为定值)时的最值求解问题.
(1)直接应用基本不等式化归转化求最值
若待求式的和或积为定值,则可以直接应用基本不等式求解.使用公式时应注意基本不等式成立的条件.
例4已知x>0,y>0,且满足3x+2y=12,求lgx+lgy的最大值.
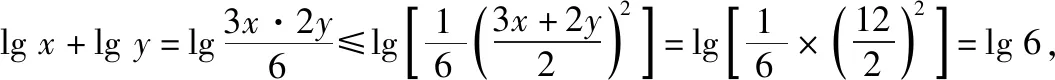
所以lgx+lgy的最大值是lg 6.
(2)应用不等式化归转化的技巧
基本不等式的一个主要功能就是求两个正变量和与积的最值,即所谓“和定积最大,积定和最小”.但有的题目需要利用基本不等式的变形求最值,有的需要对待求式作适当变形后才可求最值.
(ⅰ)加上一个数或减去一个数使和或积为定值.
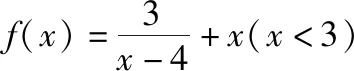
A.-4 B.1 C.5 D.-1
解:由x<3,得3-x>0,所以
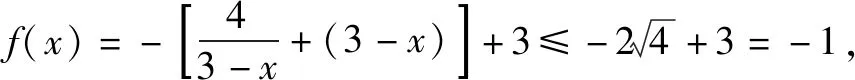
所以f(x)的最大值-1.故选:D.
(ⅱ)平方后再使用基本不等式.

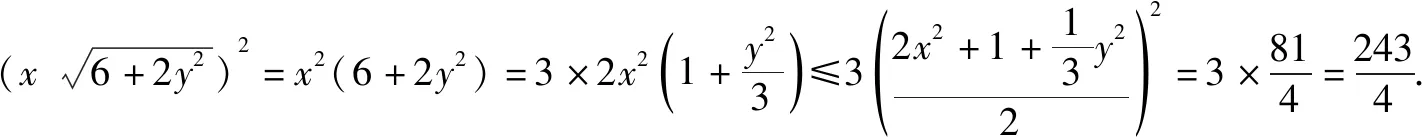
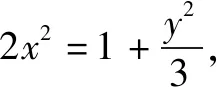
(ⅲ)用“1”的代换法化归转化求最值.

解:因为x>0,y>0,所以
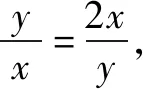
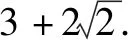
3 结语
本文中基于本真课堂系统研究了如何运用化归思想方法求解最值问题,同时将最值问题通过相互转化的方法使解题思路变得简单易懂.通过研究可以得出,最值问题解题思想方法的学习,不仅可以积累解题经验,还可以锻炼思考能力和开拓创新能力.因此,最值问题是极其具有研究意义的,也是非常重要的.

