高考数学对球体考查的新动向

西安市经开第一中学 侯丽莎

2022年高考数学学科的命题在践行立德树人为根本教育任务的同时，新情境、数学文化、知识交汇等成为一道亮丽的风景线.高考试题情境紧密联系生活实际，突出数学文化的引领作用，不同模块的知识交汇成为新的命题动向.

以往高考中与球体有关的考查，主要以确定球心位置和球半径为背景，以球体的体积和表面积计算为主要考查内容，涉及柱体、椎体的切、接问题，考查方式以选择、填空题为主.随着新高考的改革，球体与台体的切、接问题已成为基础考点，在考查球体基础知识的基础上，又出现了结合学科内在联系和知识的综合性，侧重于知识交汇的命题设计[1].既对球体基础知识的考查达到必要的深度，又把不同模块的数学知识交汇融合，通过数学知识的类比、联想、迁移和应用，体现对数学知识整体性的综合理解与灵活应用.

1 球体与集合的交汇

例1(2022·北京卷·9)已知正三棱锥P-ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合.设集合T={Q∈S|PQ≤5}，则T表示的区域的面积为( ).

分析：本题考查以P为球心，5为半径的球被底面ABC所截，求得截面圆的半径后再求区域的面积.

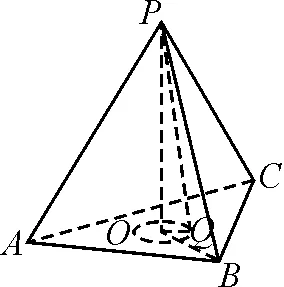
图1

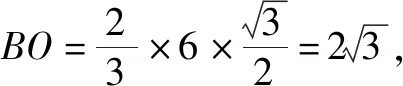
故选：B.

2 球体与不等式的交汇

例2(2022·全国乙卷·文12理9)已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O的球面上，则当四棱锥的体积最大时，其高为( ).

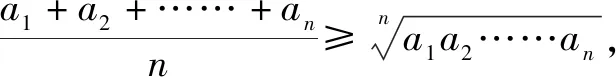
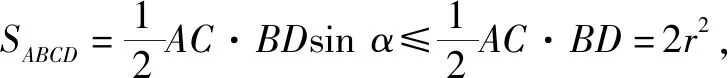
故选：C.

3 球体与旋转体的结合

例3(2020·新课标Ⅲ·文16理15)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为.

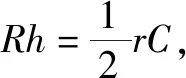
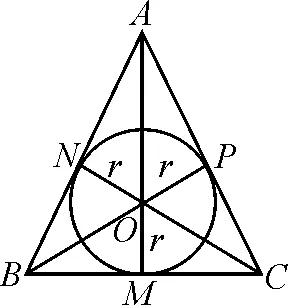
图2

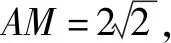
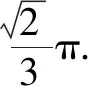
4 球体与多面体的结合

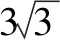
A.100πB.128π

C.144πD.192π

分析：本题考查球的表面积计算公式.根据题意可以利用正三角形性质求出正三棱台上下底面外接圆的的半径，根据球心距、底面外接圆的半径以及球的半径之间的关系建立等式，可以求出正三棱台外接球的半径，从而求得球的表面积.

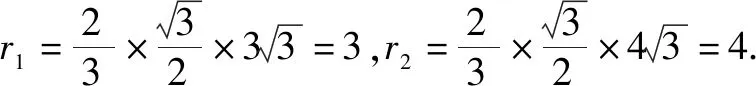
故选：A.

高中数学课程知识以单元或模块的形式呈现，两个(或多个)知识为什么会产生交汇，关键是要理解数学的本质，突破知识界限，活跃思维方式，感受数学是一个整体.

那么引起知识交汇的原因又有哪些呢？笔者从以下几个方面进行分析.

①数学文化的渗透，可以从不同的角度拓展学生对数学知识的认识，开阔学生思维，促使学生去创新，去思考，弘扬数学人文精神，继承传统.因此，数学文化成为多个数学知识交汇融合的一种载体.

②核心知识如集合、函数、不等式等在各自的发展过程中相互联系，始终是贯穿高中数学知识的主线，揭示了知识与知识之间的内在联系，这种联系能使我们运用不同的数学知识解决同一个问题.因此，核心知识的应用是众多知识交汇的焦点.

③思维导图，可让各模块之间的联系更加紧密，焦点集中，层次分明，节点相连，把零散的知识有机整合，形成系统.因此，思维导图为众多知识交汇牵线搭桥.

④思维方式的不同，解题时捕捉到的题目信息与大脑中原有的信息有效结合方式不同，所产生的的解题思想就不同.把握数学解题中的通性通法，科学有效地构建解题思维链，数学思维方法的应用是众多知识交汇的核心.

总之，2022年高考数学对球体知识的考查多以球体为背景，创设命题情境，突破知识界限，更巧妙、更新颖地交汇命题，是2022年高考数学命题的一个新动向.一线数学教师在教学中应予以重视.