利用标准差赋权组合模型预测大宗货物运输需求
崔淑华,侯慧君,武慧荣
(东北林业大学 交通学院,哈尔滨 150040)
2021年12月,国务院印发《“十四五”节能减排综合工作方案》,提出要加快大宗货物运输“公转铁”“公转水”,实现节能降碳减污协同增效、生态环境质量持续改善。大宗货物通常是指生产量、贸易量、运输量和消费量等比较大的产品,大宗货物运输是指以能源产品、基础原材料和农副产品为流通对象,使用载运工具完成大批量基础性资源的流动过程[1]。对大宗货物运输需求进行合理预测,是进行运输结构调整方案合理设计、网络布局、运营模式创新、运输定价和效益评价等的前提和关键[2],对“十四五”节能减排目标的实现起到推动作用,为实现碳达峰、碳中和目标奠定坚实基础。
目前关于运输需求预测的研究较为成熟,主要有时间序列预测、神经网络预测和组合预测等。
常用的时间序列模型有指数平滑模型、ARIMA模型及灰色预测模型等[3],相关研究有:Smith等[4]对相关时间序列预测模型进行了研究,并将其与非线性模型进行对比分析;Duru等[5]首次将模糊时间序列模型应用于运输需求预测中;Rudakov等[6]利用向量自回归模型、直方图预测的非参数模型等,对铁路货运需求量进行预测;汤银英等[7]采用三次指数平滑法对月度货运量进行预测,以此消除随机波动等带来的影响;张立欣等[8]使用ARIMA模型对货运周转量进行分析与预测;胡洁琼等[9]使用“专家建模”模型对时间序列进行拟合,得出准确率高的预测模型;Wan等[10]利用弹性系数法以及灰色模型对客货运进行预测;薛桂香[11]基于灰色GM(1,1)模型对湖北省公路零担运输需求量进行预测。指数平滑法对数列长度没有要求,但它的局限性在于不能考虑其它因素对运量变动的影响,而且一般仅适用于在数列变化比较稳定时做近期预测;ARIMA模型需要大量的历史数据且预测精度偏低;灰色预测模型具有所需样本数量少、运算简便的优点,适用于短中期预测。
关于神经网络预测方法:Carbonneau等[12]利用机器学习的神经网络、递归神经网络和支持向量机三种方法,并结合多元线性回归、移动平均等方法对供应链末端物流量进行预测;张渊[13]基于贝叶斯算法构建神经网络模型,对浩吉铁路煤炭运输需求进行分析预测;Guo等[14]采用指数平滑法对影响因素进行预测,通过GA算法优化的GRNN参数对铁路货运需求量进行预测;宋苏民等[15]利用RBF神经网络对全国铁路货运量进行预测;Sun等[16]选出17个铁路货运量的影响因素输入到GRNN模型,使用粒子群算法搜索参数,并证明了模型的有效性。以上神经网络预测模型适用于非线性和复杂的情形下,且需要设定较多参数,训练过程较为繁杂。
关于组合预测方法:李晓利等[17]构建了改进的灰色神经网络组合预测模型,克服了单一预测模型的缺点,并对煤炭物流需求进行预测;孙越等[18]基于ARMA-LSTM组合模型对铁路客运量进行对比预测;王冠智等[19]基于DWT-WFGM(1,1)-ARMA组合模型对陕西省和内蒙古自治区的农业用水量进行预测,并进行对比分析;Li等[20]选出3个铁路货运量的影响因素,提出了一种支持向量机和神经网络的组合预测模型,并证明了其预测的精准性;Wang等[21]通过对影响铁路货运量的因素进行灰色关联分析,选出其中的关键因素,并提出了一种基于遗传算法和神经网络的组合预测模型;Nieto等[22]将多种时间序列模型比较后得出ARIMA+GARCH+Bootstrap组合预测模型在预测美国航空客运量时表现最佳。组合预测模型能将各预测模型的优势进行整合,从而获得相对于单一模型而言更高的预测精度。
上述运输需求预测研究均以运输量的历史数据为基础直接进行未来值的预测,未能考虑运输供给不能满足需求时的误差。文中采用基于关联因素预测生产量,结合产运系数分析的方法进行大宗货物运输量的预测研究。由于多元线性回归分析能够综合考虑各个因素对预测结果的影响,不需要很复杂的计算,但对于非线性部分无法体现,MLP神经网络能够处理复杂的非线性问题,弥补多元线性回归模型的缺点。又因为灰色预测模型对短期预测有较高精度,运算简便,适合对文中的粮食产量影响因素进行预测,因此,提出基于标准差法将多元线性回归预测模型与GM(1,1)-MLP神经网络预测模型相结合的组合预测模型,并对哈尔滨粮食运输需求量进行预测。
1 基于标准差法组合预测模型的建立
1.1 多元线性回归预测模型
多元线性回归分析是指在相关变量中将一个变量视为因变量,其他一个或多个变量视为自变量,建立多个变量之间的线性数学模型数量关系式,并利用样本数据进行分析的统计分析方法[23]。设因变量为Y,影响因变量的k个自变量分别为Xk,假设每一个自变量对因变量Y的影响都为线性,则总体回归模型如式(1)所示。
Y=β0+β1X1+β2X2+…+βkXk+ε
(1)
1.2 GM(1,1)模型
灰色预测模型是通过少量、不完全的信息,建立数学模型并做出预测的一种预测方法。该模型在多个领域得到广泛应用,适用于时间短、数据量少、数据不需要典型分布规律的情况,对短期预测有较高精度,不适合随机波动较大的数据。
GM(1,1)表示模型为一阶微分方程,且只含有1个预测变量的灰色模型,其预测的一般步骤[24]如下所述。
步骤1:一阶累加生成。设有变量为x(0)的原始非负数据序列
x(0)=(x(0)(1),x(0)(2),…,x(0)(n))
则x(0)的一阶累加生成序列为
x(1)=(x(1)(1),x(1)(2),…,x(1)(n))
其中

(2)
步骤2:构建数据矩阵B和矩阵Y

(3)
步骤3:利用最小二乘法解灰参数得
(4)
步骤4:建立灰色预测模型,GM(1,1)模型的白化形式方程为

(5)
将求得的a,b带入式(5)并求该方程,得到GM(1,1)预测模型为

则有x0的时间响应式为

(8)
1.3 MLP神经网络模型
多层感知器是一种基于神经网络的算法模型,基本结构包括输入层L1、隐含层L2和输出层L3,如图1所示。每个输入节点与输出节点都通过加权链相连接,训练多层感知器就是不断调整加权链的权值过程,直至能够较好地拟合训练数据的输入输出关系为止[25-26]。

图1 MLP神经网络基本结构


图2 双曲正切激活函数
多层感知器需通过不断调整权值参数w来完成学习过程,直至输出和训练样本的实际输出相一致,权值调整算式为
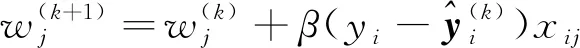
(9)


1.4 组合预测模型
1.4.1 组合预测模型介绍
将多元线性回归预测模型与GM(1,1)-MLP神经网络模型并联形成组合模型,分别赋予不同的权重,组合预测模型的基本构建形式[27]为
(10)
式中:Y为组合预测值,n为预测模型数目,wi为第i种预测模型权重系数,yi为第i种预测模型预测值。
1.4.2 权重赋值方法
由于多元线性回归预测模型与GM(1,1)-MLP神经网络预测模型各自具有优点和局限性,对其进行合理的权重分配可减小局限性,提高预测精度。
权重的赋值方法主要包括AHP法、专家调查法等主观赋权法,以及标准差法、熵权法、主成分分析法等客观赋权法。主观赋权法具有较强的主观随意性,客观性较差,不适用于文中数据较精确的情况。客观赋权法根据原始数据之间的关系确定权重,具有较强的数学理论依据,其中标准差法对标准差最小的模型赋予最大的权重,相较于熵权法和主成分分析法,其计算简单且有效,故文中采用标准差法确定各预测模型权重
(11)

(12)
式中:Si为第i种预测模型的标准差,n为预测模型数目。
2 应用实例验证
2.1 数据来源
粮食为哈尔滨市大宗货物主要品类之一,进行粮食的运输需求预测可以为哈尔滨市大宗货物运输组织方案设计提供数据支持。
因此,文中以哈尔滨市粮食运输需求预测为例,验证提出的组合预测模型的可靠性。以哈尔滨市2010—2019年的粮食产量为原始数据(数据取自《黑龙江省统计年鉴》),如表1所示。

表1 2010—2019年哈尔滨市粮食产量
2.2 哈尔滨市粮食产量关联因素分析
哈尔滨粮食年产量的关联因素包括:粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积、政策因素等[28]。根据《黑龙江省统计年鉴》《哈尔滨市统计年鉴》《中国区域经济统计年鉴》查得的数据,2010—2019年的上述关联数据如表2所示。
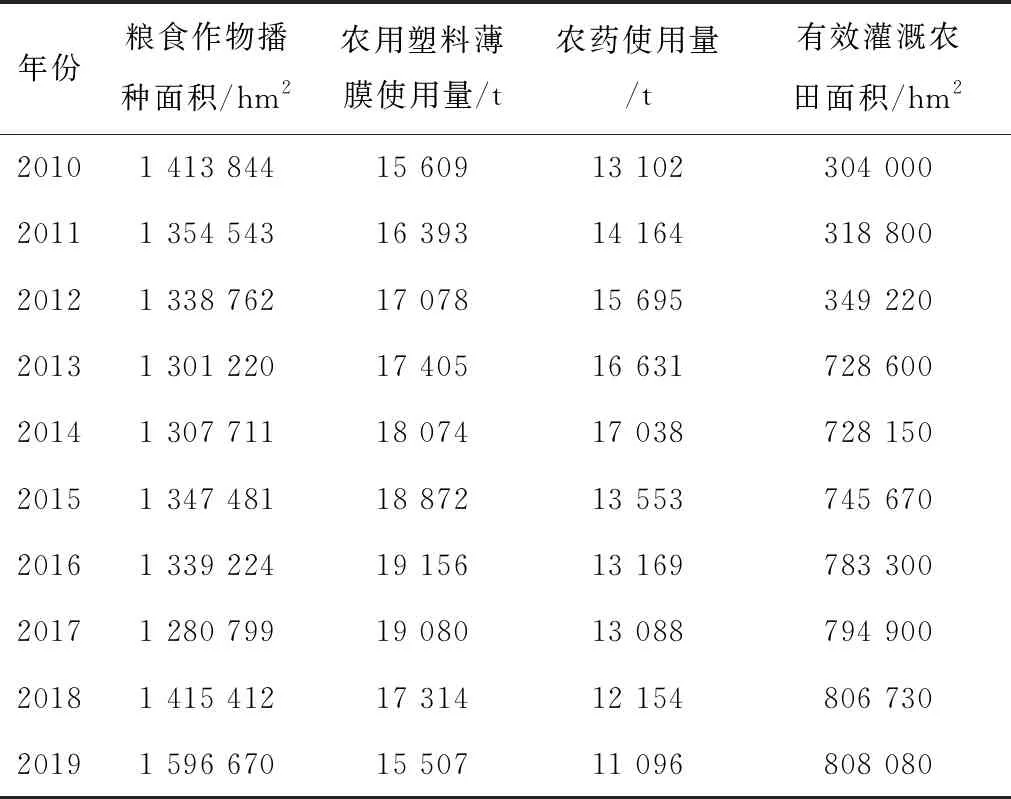
表2 2010—2019年哈尔滨市粮食产量关联因素
对粮食产量与粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积分别进行灰色关联分析,得出灰色相对关联度(见表3)。

表3 灰色相对关联度结果
由表3可知,4个关联因素的灰色相对关联度均大于0.6,说明粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积对粮食产量均有较大影响,按照对粮食产量的影响程度依次排序为:粮食作物播种面积,农药使用量,农用塑料薄膜使用量以及有效灌溉农田面积。
2.3 基于多元线性回归模型的粮食产量预测
2.3.1 模型求解及检验
将粮食产量(y)作为因变量,粮食作物播种面积(x1)、农用塑料薄膜使用量(x2)、农药使用量(x3)、有效灌溉农田面积(x4)作为自变量,进行多元线性回归运算,结果如表4所示。

表4 多元线性回归运算结果
从表4可得出哈尔滨市粮食产量的多元线性回归方程为
y=-3 632.911+0.002x1+0.123x2+
0.065x3-0.001x4
(13)
1)R2检验。对多元线性回归模型进行拟合优度检验,统计量越接近1拟合优度越高。R2计算结果如表5所示。

表5 R2计算结果
由表5可知,R2=0.939,调整后R2=0.890,接近于1,说明粮食产量与粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积之间有较强的线性相关性,拟合程度较高。
2)F检验。对多元线性回归模型进行F检验,假设H0:b0=b1=…=bn=0;H1:bi不全为0,当在显著水平α下,F值大于Fα(k,n-k-1)时,拒绝H0,即Y与xj的线性关系显著;反之,则不显著。方差分析结果如表6所示。

表6 方差分析
由表6可知,统计量F=19.189,回归平方和和残差平方和总计为268 239.631,自由度为9。取显著性水平α=0.05时,查F分布表可知,F的临界值为F0.05(4,5)=5.19<19.189,所以F检验通过。
3)t检验。首先对解释变量的检验假设:H0:b0=b1=…=bn=0;H1:bi不为0。在显著水平α下,如果|tj|l>tα/2(n-k-1),则拒绝H0,即xj对Y有显著影响,xj是影响Y的主要因素;反之,接受H0,即xj对Y无显著影响,则应剔除该因素。
从表4可以看出,t1=-3.126,t2=2.864,t3=3.086,t4=3.884,t5=-6.145,取显著性水平α=0.05时,查t分布表可知,t0.025(4)=2.776 4。因为|t1|=3.126>2.776 4,|t2|=2.864>2.776 4,|t3|=3.086>2.776 4,|t4|=3.884>2.776 4,|t5|=6.145>2.776 4,所以t检验通过。
2.3.2 预测结果
分别对2010—2019年哈尔滨市的粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积进行分析,得出回归方程为
根据式(14)~(17)预测出2010—2025年哈尔滨市粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积的值,如表7所示。

表7 2010—2025年哈尔滨市粮食产量关联因素预测值(多元线性回归模型)
根据表7和式(13)可得2010—2019年哈尔滨市粮食产量预测值(见表8)。

表8 2010—2019年哈尔滨市粮食产量预测值
2.4 基于GM(1,1)-MLP神经网络模型的粮食产量预测
采用灰色GM(1,1)预测模型对2010—2025年的哈尔滨市粮食作物播种面积、农用塑料薄膜使用量、农药使用量、有效灌溉农田面积进行预测,预测结果如表9所示。

表9 2010—2025年哈尔滨市粮食产量关联因素预测值(GM(1,1)预测模型)
基于以上模型对4个关联因素进行2010—2025年的数据预测,之后建立MLP神经网络对2021—2025年的粮食产量进行预测。
2.4.1 分区数据集
将活动数据集划分为训练集、测试集和验证集3个集合,训练集中的数据用于训练神经网络,测试集合中的数据用于监视训练过程中的错误以防过度训练,验证集合中的数据用于评估训练所得到的神经网络准确性。当数据量比较小(万级别及以下)时,常见的做法是将大约2/3 ~ 4/5的样本数据用于训练,剩余样本用于测试,由于文中的数据量较小,故将训练、测试和验证样本按70%、30%和0%的比例来划分。
2.4.2 训练模型
在满足精度要求的前提下,为提高数据训练效率,在该神经网络的体系结构中构建一个使用双曲正切激活函数的隐藏层,并选择批处理的训练方式,即运用训练数据集中的所有记录信息,以使总误差最小化。由于该方法在满足任何结束训练的条件前都需要不断调整权重,所以有可能将数据多次传递。优化算法在调整后选择了相应的共轭梯度,模型参数如表10所示。

表10 模型参数
2.4.3 预测结果
通过训练样本得到满足要求的神经网络模型,则2010—2019年哈尔滨市粮食产量的预测值如表11所示。

表11 2010—2019年哈尔滨市粮食产量预测值
2.5 基于组合预测模型的产量预测
标准差计算如式(18)所示。
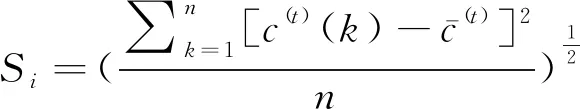
(18)
式中:n为预测模型数目,c(t)为模型残差。
根据式(18)计算两种预测模型的标准差分别为0.860 6和0.139 4,根据式(11)~(12)计算得到两种预测方法的权重分别为0.139 4和0.860 6。运用组合预测方法对2010—2019年哈尔滨市粮食产量进行预测(见表12),将3种预测模型的预测值与实际值进行对比,如图3所示。

表12 2010—2019年哈尔滨市粮食产量预测值
从图3可知,两个单项预测模型与组合模型都可以对哈尔滨市粮食产量做出较为精准的预测,均具有一定的参考价值。其中,多元线性回归模型的预测结果大体趋势和实际值相同,但仍存在较大误差,GM(1,1)-MLP神经网络模型与组合模型的预测结果和实际值的误差较小。为进一步准确对比两个单项预测模型与组合模型的预测准确性,分别计算各预测模型的平均绝对百分比误差MAPE,和方差SSE,均方误差MSE,均方百分比误差MSPE,得到结果如表13所示。

图3 各预测模型预测值与实际值对比

表13 各预测模型误差计算
由表13可知,组合预测模型的各个误差指标比所有单项预测模型都低,能够有效提高预测精度。由组合预测模型能预测出2021—2025年哈尔滨市粮食产量(见表14)。

表14 2021—2025年哈尔滨市粮食产量预测值
2.6 基于产运系数的运输需求预测
产运系数是一定时期内全社会 (或地区) 某种产品的运输量对生产量之比率,如式(19)所示。
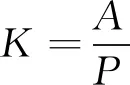
(19)
式中:K为相应产品的产运系数,A为相应产品的运输量,P为某种或多种工农业产品的生产量。
根据《2019年哈尔滨市国民经济和社会发展统计公报》,2019年年末哈尔滨市的户籍总人口数为951.3万人,其中城镇人口473.9万人,乡村人口477.4万人;根据《2020中国农村统计年鉴》,我国2019年城镇居民人均粮食消耗量110.6 kg,农村居民人均粮食消耗量154.8 kg,得出2019年哈尔滨市粮食消耗量为126.31万t;根据历史数据调研,粮食运输量约为该地区粮食产量与消耗量的差值。所以,哈尔滨市粮食产运系数为0.888 4。
通常情况下,大宗货物的运输量与其生产总量的比值(产运系数)相对稳定。结合表11和式(19)可计算出2021—2025年哈尔滨市粮食运输需求,如表15所示。

表15 2021—2025年哈尔滨市粮食运输需求
3 结 论
针对单一模型预测方法的局限性,提出了基于标准差法赋权大宗货物运输量的组合预测模型,以哈尔滨市粮食产量历史数据对所建立的组合预测模型预测精度进行了分析与验证。
1)公路货运车辆,特别是中重型柴油货车的排放是主要的大气污染源。近几年运输行业转型升级取得积极成效,但仍存在综合运输体系结构不合理、公路货运量占比过高等问题。对大宗货物运输需求进行合理预测,是进行运输结构调整方案合理设计的前提和关键,对“十四五”节能减排目标的实现起到推动作用。
2)文中构建的组合预测模型与单一预测模型相比,其平均绝对百分比误差(MAPE)、和方差(SSE)、均方误差(MSE)、均方百分比误差(MSPE)均小于另外两种单一预测模型。预测值和真实值偏差更小,证明该模型具有较高的预测精度。
3)该组合模型预测结果反映了哈尔滨市的粮食产量、运输需求量以及变化趋势,可为大宗货物运输业务发展规划、优化大宗货物运输组织、合理配置运输装备等提供一定理论依据。
4)基于已取得的研究成果,对不同种类大宗货物产量的关联因素进行更全面的分析,对大宗货物产运关系进行更深入的研究,从而进一步优化大宗货物运输需求预测模型,这也是后续研究的重要方向。

