疫情风险防控下医疗废物运输选址-路径优化

赵佳虹，黄淑媛，陈志伟，肖景文

(1.广东工业大学 土木与交通工程学院，广州 510006；2.暨南大学 管理学院，广州 510632；3.四川省交通建设集团股份有限公司，成都 610000)

2022年1月，全球“新冠”疫情医疗废物产量突破1 110万t·d-1，超过30%的国家陷入医疗废物运能短缺困境[1]。在常态化疫情防控下，优化医疗废物运输成为当前亟待解决的问题。疫情医疗废物具有感染性，如果运输管理不当，极易诱发疫情风险[2]。因此，在城市路网的基础上，优化医疗废物运输的设施选址及能力配置、运输路线和运量分配，是有效防控疫情风险的必要途径。

近年来，国内外学者针对医疗废物运输选址-路径问题进行了大量研究。在风险度量方面：黄丽霞等[3]采用了“暴露人口吨数”模型，描述了风险影响的深度和广度；Masoud等[4]以暴露人口数量衡量了运输潜在风险；Zahra等[5]将运输风险界定为不受公众欢迎的有害影响；赵佳虹等[6-7]先后构建了时变“环境-人口”风险度量模型和“环境-社会-财产”多源风险度量模型;朱海彤等[8]考虑运输时间对风险的影响，构建医疗废物运输风险度量模型。在系统建模和优化求解方面：董乾东等[9]考虑多时间周期、多种医疗废物及处理技术等因素，构建医疗废物管理系统网络的多目标规划模型；Kargar等[10]建立了总成本最小、处理技术选择最佳和医疗废物存储量最小的线性模型；Hassanpour等[11]研究了具有随机中断路段、时变参数和配送时间窗的危险物品选址-路径问题;Zahiri等[12]研究了考虑行程时间、等待时间和可用容量不确定的含设施选址的危险品网络设计问题，采用平均绝对偏差可能性规划模型在解决问题中的不确定性;Budak等[13]则以总成本最小化为目标，通过构建混合整数模型来优化医疗废物管理设施的最佳建设数量和位置。由于医疗废物运输选址-路径问题属于组合优化问题，且构建的模型含有多目标，因此Teoh等[14]提出了一种数据驱动的多目标差分进化算法，优化了含有安全容量限制的车辆路径问题；Shahrzad等[15]融合了动态规划和情景鲁棒优化方法，解决了不同情景下的危险品运输路径优化问题。

在常态化疫情防控背景下，上述研究成果主要存在以下不足：风险度量不适用于评估疫情医疗废物的运输风险;忽略了社会公众的感知差异;系统建模忽略了城市路网结构和既有运输系统;模型和算法的敏感性和稳定性分析不足。文中基于疫情风险防控，以城市医疗废物运输网络为基础，构建疫情风险最小和成本最小目标，协同优化医疗废物运输的临时设施建设位置、能力配置、路线选择和运量分配问题。主要根据医疗废物的感染性、环境传播性和公众感知差异性，设计医疗废物运输的疫情风险度量模型；结合城市路网的局部连通特征，构建疫情风险最小和成本最小的多目标医疗废物运输选址-路径模型；针对模型计算复杂性，设计基于带权重的目标规划方法和自适应遗传模拟退火算法的多目标优化算法；最后，结合武汉实际及多个测试算例，验证模型和算法的有效性、参数敏感性和计算稳定性。

1 疫情风险度量

疫情期内产生的医疗废物含有感染性病毒，若发生泄漏，病毒会以大气环境为载体，在一定的空间范围内进行立体式传播，处在该范围内的社会公众通过呼吸方式感染一定浓度的病毒，会受到风险影响。文中借鉴感知风险模型[16]和环境风险模型[17]的构建原理，将医疗废物运输疫情风险定义为：基于不同的公众感知系数，在医疗废物运输系统中，因泄露事故直接受到影响的人口数量与其吸入的病毒浓度。显然，疫情风险可描述为：在既定感知系数下，一定范围内的人口数量与病毒浓度的乘积。若将医疗废物的运输设施i和路线(i,j)分别视作风险源，则对应的疫情风险分别表示为

RNi=PNi×μNi

(1)

RAi，j=PAi，j×μAi，j

(2)

式中：PNi，PAi，j为设施i和路线(i,j)周边人口数量；μNi，μAi，j为设施i和路线(i,j)周边病毒浓度。

由于社会公众对于风险感知存在不同程度上的差异，文中引入感知差异系数q表示公众对风险的厌恶程度。如图1所示，在运输系统的关键设施上，人数的统计范围是以设施i为圆心、λ为半径划定的圆形；在运输路线上，人口数量统计范围是以路线(i,j)为中轴线、路线长度Di，j为长边、2λ为宽边的矩形。若将设施i和路线(i,j)周边的人口密度分别设定为ρNi和PAi，j时，则在感知差异系数q的条件下，医疗废物运输设施i和路线(i,j)周边一定范围内的人口数量可分别表示为

图1 人口数量统计范围

PNi=(ρNi)q×πλ2

(3)

PAi，j=(ρAi，j)q×2λ×Di,j

(4)

另外，设施i和路线(i,j)周边病毒浓度与扩散体积有关，在关键设施上，病毒扩散体积是以设施i为圆心、λ为半径划定的半球体；在关键路线上，病毒的扩散体积则是以路线(i,j)为中轴线、λ为半径的半圆柱体。当设施i和路线(i,j)上储运的医疗废物量分别为wNi和wAi，j时，其泄露的病毒浓度可分别表示为

(5)

(6)

整合式(3)～(6)，并代入到式(1)～(2)中，可推导出设施i和路线(i,j)上的疫情风险分别为

(7)

(8)

2 数学模型构建

2.1 问题描述

如图2所示，医疗废物运输系统是基于城市既有路网生成的一个含有转运中心、回收中心和处置中心的3层网络结构。由于疫情的突发性和演化不稳定性，运输系统的能力负荷存在极大不确定性，因此，需要在现有系统中进行设施选取、临时设施增加和设备升级。基于疫情风险防控，优化确定医疗废物运输系统临时转运中心的最佳建设地点、转运中心启用对象，并设计医疗废物运输路线和运量分配方案。

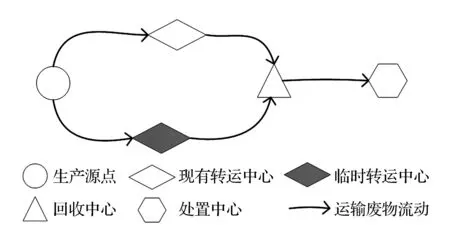
图2 城市医疗废物运输系统结构

2.2 基本假设

文中构建的模型在以下基本假设条件下开展：

1)研究区域为一个城市道路运输网络；

2)转运中心成本与能力成正相关；

3)道路及设施点附近居民为风险影响对象；

4)外部天气条件相对稳定；

5)设施选址不考虑地理等隐性因素影响。

2.3 符号说明

模型构建中用到的符号及含义说明如表1所示。

表1 符号说明

2.4 多目标选址-路径优化模型

(9)

(10)

(11)

(12)

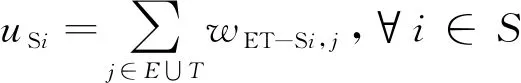
(13)

(14)

(15)

wS-Bi，j=(1-θi)uBi，∀i∈S，∀j∈B

(16)

(17)

(18)

(19)

(20)

yi,l,zi,l,xg,i,l={0,1},∀g∈G,∀i∈E∪T，∀l∈L

(21)

wG-Sg,s，wG-ETg,i,l,wET-Si,s,wS-Bs,b，uETi,l,uSs,uBb≥0,∀g∈G,∀i∈E∪T，∀s∈S,∀b∈B，∀l∈L

(22)

式(9)～(10)为目标函数，其中式(9)为最小化疫情风险，主要包括医疗废物运输疫情风险和转运中心处理医疗废物的疫情风险；式(10)为最小化成本，主要包括转运中心的建设成本和运营成本，以及医疗废物运输成本。式(11)～(14)为流量平衡约束。其中，式(11)表示从生产源点到转运中心的废物量等于源点的废物总量；式(12)表示转运中心的废物量等于运输的废物量；式(13)表示从转运中心到回收中心的废物量等于回收中心的废物量；式(14)表示回收中心运往处置中心的量等于处置中心的量。式(15)为保证经过转运中心的废物量等于其流入回收中心的量。式(16)表示回收和处置中心的流量平衡。式(17)～(18)为转运中心的容量约束。式(19)表示任意特定能力等级的转运中心的流入废物量等于分配给该中心的来自生产源点的废物量。式(20)表示每个源点的废物只能最终运到一个配置了唯一能力等级的转运中心。式(21)～(22)为决策变量定义域。

3 求解方法

文中构建了一个多目标混合整数非线性模型，模型含有两个不同量纲的子目标，却存在非线性约束条件。根据模型特征，设计求解思路为：首先线性化处理原模型的非线性约束条件，然后采用带权重的目标规划方法进行多目标转化，最后引入自适应遗传模拟退火算法求解转化后的数学模型。

3.1 模型线性化处理

模型中式(18)为非线性约束条件，且式子右侧是由两个二元变量相乘形成，首先设定新的二元变量oZYj，l，用其代替zj，l×yj，l转化为线性方程，将模型的非线性约束转化为下式

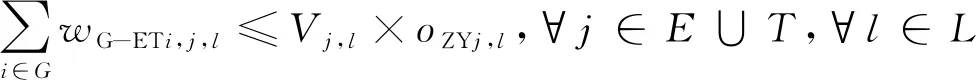
(23)

oZYj，l-zj，l-yj，l+1.5≥0,∀j∈E∪T,∀l∈L

(24)

1.5×oZYj，l-zj，l-yj，l≤0,∀j∈E∪T,∀i∈L

(25)

oZYj，l={0,1}，∀j∈E∪T，∀l∈L

(26)

其中，式(24)～(25)联合表示医疗废物只能从生产源点运输至确定建立的临时转运中心。

3.2 基于带权重目标规划的多目标转化

综合考虑不同决策者的目标偏好差异和Pareto最优解集特征，引入权重系数，采用目标规划方法将构建的多目标模型转化为单目标优化模型，然后采用自适应模拟退火方法进行模型求解，具体步骤设置如下。

步骤1：设集合G，E，T，S，D和C，令X为决策变量向量，Z1(X)和Z2(X)为目标函数，F为可行域。

步骤2:输入模型已知的定量参数。

步骤4:设置无量纲化因子σ1和σ2为

(27)

(28)

步骤5:根据决策者偏好，设定两个优化目标的权重系数λ1和λ2，且λ1+λ2=1。

(29)

3.3 自适应遗传模拟退火算法求解步骤

设定适应度函数为式(29)中的目标函数，自适应度调整设计遗传算法交叉、变异概率为

(30)

(31)

将以上参数与模拟退火算法相结合，fmax为当前种群中目标函数的最大适应度值；favg为当前种群适应度值的平均值；f′为选中的交叉个体中的较大适应度值；f为变异个体的适应度值；参考文献[18]的取值，将交叉、变异概率计算的固定参数设为cC1=cC2=0.9，mM1=mM2=0.5。具体步骤设计如下。

步骤1：初始化最大种群数目，初始温度和迭代次数等参数。

步骤2：分别采用0-1编码和整数方式对设施选址和运量分配问题进行混合编码，初始化种群染色体。

步骤3：以式(29)中已经转化的目标函数作为适应度函数，计算种群中个体适应度。

步骤4：判断是否符合终止条件，若达到迭代次数，则终止计算，输出最终结果；否则，转入步骤5；

步骤5：通过选择、交叉、变异产生新个体，其各项具体设定如下所述。

1)选择：采用轮盘赌的方法选择适应度高的染色体个体作为父代遗传给子代，从而使子代继承父代的优秀基因，通过不断选择得到最高适应度的染色体个体。

2)交叉：采用单点交叉的方式在奇数位对两个父代染色进行重组产生两个新的子个体。两个子个体继承交叉位置前的父代基因，交叉位置后奇数位继承父代染色体与交叉位前的不同基因，然后填入漏掉的基因；偶数位的基因随着奇数位的基因做对应位置的继承与填入操作。

3)变异：随机选取一对包含应急物资调度量部分和调度访问顺序的染色体基因,采用随机调换位置的操作对染色体上的基因进行变异。

步骤6：判断子代个体适应度。若子代小于父代，则接收个体，否则以概率接收,形成新种群。

步骤7：降温处理，转至步骤3。

4 算 例

结合实例和测试算例来验证模型和算法的有效性。所有计算在CPU为Intel core i5-7200U 2.50GHz和RAM为4.00 GB的个人电脑上执行，通过MATLAB编程，结合YAMIP调用CPLEX12.10进行编码实现。

4.1 武汉实例

基于武汉疫情医疗废物管理实践，在ArcGIS系统上随机选取54个节点，其中生产源点30个(G1—G30)，现有转运中心12个(E1—E12)，临时转运中心候选点7个(T1—T7)，回收中心3个(S1—S3)，处置中心2个(D1和D2)。根据文献[18]和文献[19]的参数设定，医疗废物在回收中心的回收比例为10%，各生产源点的医疗废物产量以武汉市高峰时期单日产生247 t为例，随机产生30个在[5，11]之间且和为247的数，并分别分配到30个生产源点中，各节点医疗废物产量如表2所示。根据武汉市疫情前医疗废物的设计处置能力情况，将处置能力设为50 t·d-1，确定感知系数q为4.94。结合参考文献[18]的参数设定规则，设危害半径λ为800 m，转运中心运营成本1.2元·t-1，生产源点和转运中心间的运输成本为20.27元·(t·km)-1，转运、回收和处置中心间的运输成本0.84元·(t·km)-1，现有和临时转运中心候选点数据如表3～4所示。

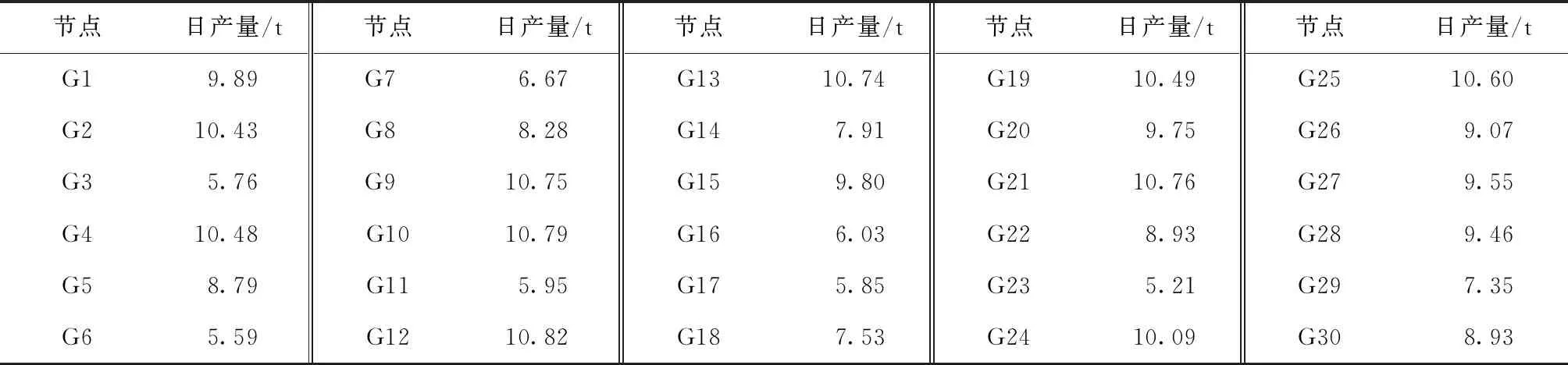
表2 各生产源点的医疗废物产生量

表3 现有转运中心候选点数据

表4 临时转运中心候选点数据

对政府部门决策者而言，建设医疗废物运输系统的第一目标是最小化疫情风险；而对于相关运输企业而言，第一目标是最小化成本。最小化风险和最小化成本对应的计算结果如表5所示。使用带有权重系数的目标规划法进行多目标转化求解，将权重系数λ1和λ2的组合共分为9种，根据参考文献[20]的取值，设置初始种群数量为30，交叉和变异概率分别为0.8和0.03 ，最大进化代数为200。如表6所示，使用自适应遗传模拟退火算法依次求解相应的权重组合，都可在25 s内求得其对应的计算结果。文中设计的求解方法可为不同偏好的管理者提供多个有效优化方案。当权重系数λ1取值在0.1～0.6时，方案总疫情风险和总成本变化趋势较为平稳。当λ1为0.6和0.7时，疫情风险和成本值有明显差异。若决策者为风险偏好型，可采用λ1=0.7的方案，若为成本偏好型，可采用λ1=0.6时的方案。

表5 单目标计算结果

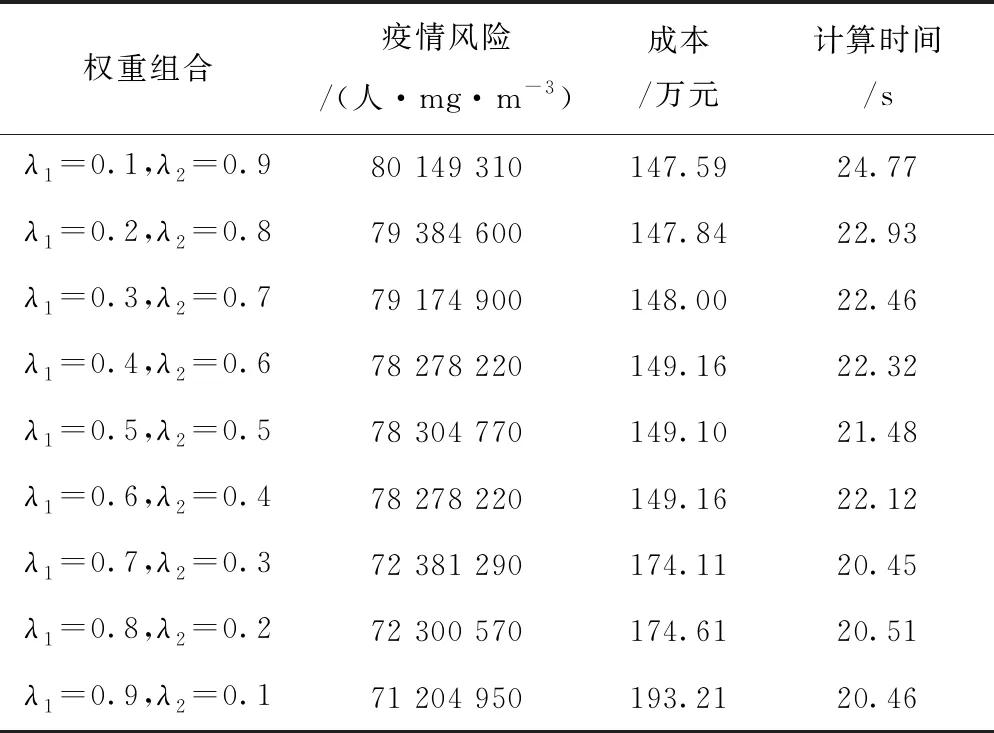
表6 带权重系数的目标规划法计算结果

4.2 测试算例

基于武汉实例，由MATLAB在50 km×50 km的区域内随机生成数据，拓展设计10个测试算例，进一步验证模型和算法的有效性。

1)疫情风险模型效用分析。分别采用暴露人口数(测试1)和暴露人口吨数模型(测试2)，在最小化风险时，对比方案总成本。如表7所示：相较于传统风险模型，新模型的优化方案可减少1.4%的总成本和34.25%的求解时间。

表7 风险度量模型效用计算结果对比

2)参数敏感性分析。根据参考文献[20]的设定方式，设定测试3和4的风险感知系数q为1.23和1。设定λ1=0.5，采用设计算法求得不同感知系数的优化方案。如表8所示：感知系数对疫情风险的影响更大，对成本影响较小。

表8 不同感知系数的敏感性分析结果

3)计算稳定性分析。各测试算例节点数量(生产源点，现有转运中心候选点，临时转运中心候选点，回收中心，处置中心)分别为：小规模测试算例(15,6,3,2,1)，中规模(60,24,14,6,4)，大规模(90,36,21,9,4)和特大规模(120,20,20,20)，各节点的参数设置参考武汉实例进行随机生成。计算结果如表9所示：虽然随着计算规模的扩散，优化方案的求解时间增加，但总体求解时间应控制在580 s以内，因此，文中设计的求解方法具有较高的计算稳定性，能够在有效的计算时间范围内，求得GAP值在7.25%以内的优化方案。

表9 不同规模问题的计算稳定性分析结果

4)求解方法对比分析。沿用武汉实例的参数设置和计算规模，基于同样的计算环境，分别采用基于线性加权的多目标优化方法和基于TOPSIS的多目标优化方法进行模型求解，对比分析测试算例的优化结果。如表10所示：相较于线性加权的常规多目标优化方法，新算法虽然在计算时间上会多10.15 s，但选址-路径方案的GAP却可降低6.71%；相较于TOPSIS法的求解方法，在新算法可以减少近62.13%的计算时间基础上，求得出GAP更低的优化方案。由此可见，新算法具有更为高效的求解效率。

表10 不同求解方法的计算结果对比

5 结 论

为降低疫情医疗废物的病毒传播风险，基于疫情风险防控目标，提出了医疗废物运输的选址-路径模型，协同优化了医疗废物转运中心选址和运输路径运量分配决策。

1)根据医疗废物感染性、环境传播性和公众感知差异性，确定了医疗废物运输的疫情风险定义，并建立了风险度量模型。

2)根据城市路网特征，构建了疫情风险最小和成本最小的多目标选址-路径优化模型。

3)整合带权重的目标规划方法和模拟退火算法，设计了多目标优化算法求解步骤。

4)结合武汉实际算例和多个测试算例，验证了新建模型和算法的有效性，计算结果表明：新模型和算法能够在25 s内为疫情防控提供多个有效方案，且具有参数敏感性和计算稳定性。相较于传统风险模型，新模型可减少1.4%的总成本和34.25%的求解时间；相较于常规多目标优化方法，新算法可减少约62.13%的计算时间，并求得GAP更低的优化方案。