常微分方程中的变换方法探究

杨继昌，陈广生，沈柳平，莫明忠，马岱君，周昌永

（广西科技师范学院数计学院，广西 来宾 546199）

0 引言

常微分方程是一个理论研究和实际应用并重的学科，它在数学专业中具有很重要的地位，在体现客观自然规律和解决实际问题方面也不可或缺[1]。

在高校数学类或理工类专业的《常微分方程》教材中列举了很多种形式的常微分方程，其中最基本的一种就是变量分离方程，只需要用初等积分法即可求解。但是其他类型的常微分方程，我们最常用的方法就是变换方法。本文将对变换方法进行讨论和研究，阐明它在求解常微分方程中的重要性。

1 一阶常微分方程的变换方法及解题步骤和

1.1 变量分离法[2]

变量分离，其实质就是将未知函数或因变量与自变量分离出来，使等式的一边为未知函数的导数，另一边为自变量的导数形式.然后通过微分的逆运算，即两边同时积分，再逐步求出未知函数。

解：根据变量分离理论，此常微分方程可以变量分离为以下形式：

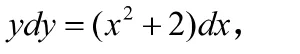
变量分离方程的基本形式为：

1.2 变量代换法

变量代换法的主要思想是对于一些微分方程形式上不是变量分离方程，若通过适当的变量代换后可以化为变量分离方程，再通过变量分离方程的求解方法求出变量代换后的方程的解，最后再将变量代换的解代回原来的变量就可以得到原方程的解。

1.2.1 齐次微分方程[3]

1.2.2 非齐次微分方程

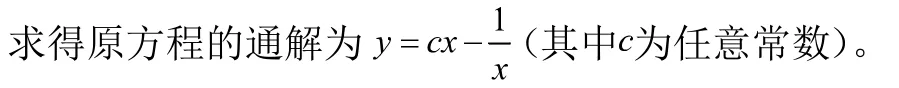
以上是对于形如（9）、（12）、（14）、（15）、（16）的微分方程求解问题中的变量代换法的应用，当然，还有其他一些类型的微分方程应该也可以通过变量代换法进行求解，限于篇幅，笔者不再赘述。

1.3 常数变易法

1.3.1 非齐次线性微分方程

1.3.2 伯努利微分方程[11]

1.4 分项组合法[12]

分项组合就是把每一项都分开，然后观察其中的每一项，先把那些本身就已经构成全微分的项分出来，再把剩下的所有项凑成全微分，这种方法也叫凑分法。

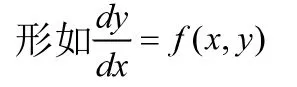
的方程可以写成一阶微分方程的形式：

当方程的左边正好是某个二元函数的全微分时，该方程称为恰当微分方程。某方程为恰当微分方程的充要条件是：

我们在判断所需求解的方程为恰当微分方程之后，便可以通过分项组合的方法来进行求解。

1.5 积分因子法