涡旋压缩机舌簧阀动态工作特性研究
马峰,董迎晖,胡兆稳,梅亚
(1.合肥工业大学机械工程学院,合肥 230000;2.合肥安信瑞德精密制造有限公司,合肥 230031)
0 引言
涡旋压缩机具有效率高、体积小、转速高等特点,被广泛应用在汽车空调中。阀片作为压缩机中的关键部件,其运动规律的好坏将直接影响涡旋压缩机的工作效率。舌簧阀按照运动特性及不同的简化条件,可以视为单质点力学系统、连续梁力学系统及薄板横向振动力学系统等[1-3]。在把舌簧阀看作单质点单自由度模型的基础上,Liu G等[4]基于真实气体状态方程建立了描述吸入阀动态过程的数学模型。杨乐之[5]应用Bredesen气阀动力学模型求解,结合阀片自身特点获得了微型往复式空压机舌簧阀的简化计算方法。林槑等[6]考虑了气流阻力,并通过实验验证引入非黏性阻尼项对阀片运动方程的修正,使得阀片的数学模型更简单,而且具有明确意义。Wambsganss等[7]基于弯曲梁模型,对舌簧阀工作特性进行了计算和实验。Mu Guangyu等[8]将有升程限位器的舌簧阀当作卷绕模型,并且还考虑了舌簧阀和阀座间油液的黏滞效应对阀片动态特性的影响,通过建立阀位移测量实验系统,验证了该模型与单质点单自由度模型相对比,在描述阀门动力学方面更加准确有效。吴丹青[9]把舌簧阀视作弹性薄板,从机械振动理论和热力学关系推导出舌簧阀运动规律的理论计算结果,其理论计算结果和实测曲线吻合程度符合要求。以上都是通过建立模型来提高排气阀性能的研究,但在模型建立和前期处理方面较为复杂,且缺少舌簧阀参数对阀片工作特性影响的量化分析。
为了更加符合工程实际,深入分析涡旋压缩机排气阀的舌簧阀工作过程中的动态特性,本文基于弹性薄板横向振动理论,运用模态叠加方法建立舌簧阀的运动模型,在实现振型叠加的时候,把舌簧阀看作悬臂薄板,获取其前3阶振型函数。通过MATLAB利用四阶龙格库塔法对舌簧阀的运动数学模型进行求解,获取舌簧阀动态响应特性,用来分析舌簧阀的可靠性,提高阀片的使用寿命,以更加简便并且更加准确地描述涡旋压缩机舌簧阀工作过程方法,同时指导舌簧阀的设计及性能优化。
1 涡旋压缩机舌簧阀数学模型
1.1 舌簧阀动力学模型
舌簧阀的长和宽远大于其厚度,可视作弹性薄板的弯曲运动,其运动方程根据有关弹性薄板横向振动理论得出
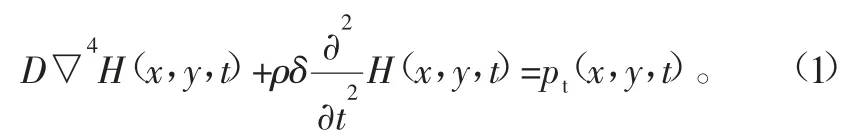

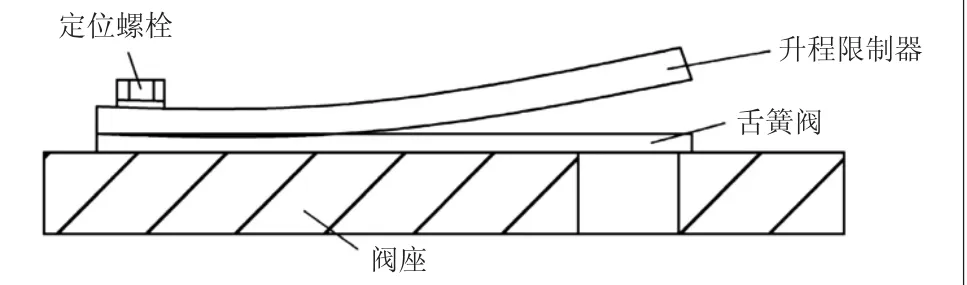
图1 舌簧阀结构图
对于式(1)直接求解比较困难,较为合适的方法是运用模态叠加法,阀片上各点的升程规律H(x,y,t)可用下式表示:

把式(2)代入式(1)并消去▽4,然后运用特征函数的正交性定理,并按照表面积的积分和多次变换,再引入一个阻尼系数ξ,通过化简计算得到[9]:
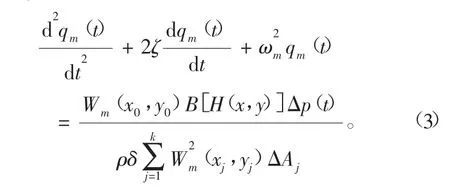
式中:B[H(x,y)]为阀片相对于阀座孔口的有效作用力面积,它是升程H(x,y)的函数;ΔP(t)为阀片上下面的压力差;(x0,y0)为阀孔中心点的坐标。
1.2 舌簧阀振型函数的获取
对于式(3)的求解,需要获取其自由振型函数Wm(x,y),对于舌簧阀一端固定一端自由,可以视作悬臂薄板来获取其各阶模态振型函数。
设l为弹性薄板长度,b为宽度,δ为厚度,根据薄板自由振动微分方程[10]:
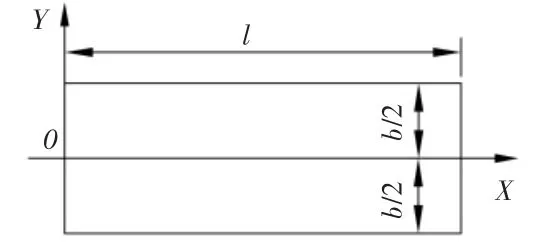
图2 弹性薄板平面图
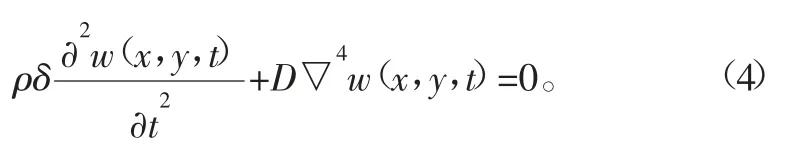
利用分离变量法求解,设
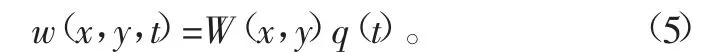
式中:W(x,y)为振型函数;q(t)为描述运动规律的时间函数。边界条件为x=0,固支x=l、y=±b/2自由,振型函数形式为

联立式(6)~式(8)获取阀片各阶模态下的振型函数。
1.3 涡旋压缩机流动微分方程
对于带排气阀的涡旋压缩机,当0≤θ≤θde时(θde为排气结束角),中心腔容积Vc为:

式中:a为基圆半径;α为渐开线发生角;h为涡旋体高度。
通过借助连续方程忽略泄漏的影响,并利用理想气体有关性质,可以推导出气流流经阀片时候的流动微分方程[11]为

联立阀片的运动微分方程和流动微分方程,运用四阶龙格库塔法,在MATLAB中编写计算程序对所联立方程进行求解。
2 数值模拟
2.1 初始条件
求解舌簧阀运动方程时,当弹力等于气体力时,阀片便有了离开阀座的趋势,此时阀片的位移、初速度和初始加速度均为0,初始条件为:
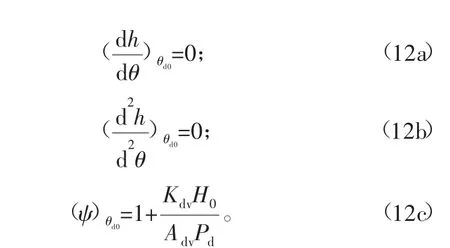
式中:θd0为舌簧阀离开阀座时对应的瞬时曲柄转角;H0为排气阀升程;Kdv为排气舌簧阀阀片刚度;Adv为单个排气阀的阀座通流面积。
对所建立的舌簧阀模型进行求解的时候,需要考虑升程限制器对于阀片运动的影响,在阀片工作过程中把升程限制器当作撞击的边界条件,可采用反弹系数来表示:
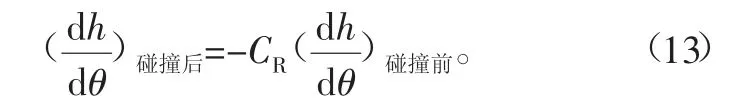
反弹系数为撞击前后阀片速度的比值,根据经验可取0.3[12]。
2.2 数值计算
涡旋压缩机转速为4000 r/min,舌簧阀材料采用山德维克碳钢阀片20C,厚度为0.18 mm,阀孔直径为7 mm,特征升程为2 mm。针对建立的弹性薄板横向振动动力学模型,采用四阶龙格库塔法在MATLAB环境下求解,计算结果如图3所示。
从图3 中可以看出,当主轴转角等于排气角的时候,阀片开启,并快速上升,当阀片与升程限位器发生碰撞的时候,阀片在反弹力的作用下回落,此时作用在阀片下端的气体力使得阀片回落到一定程度后继续上升与阀片贴合。随着气体力的逐渐减小,当气体力不足以支撑阀片回落的弹性力的时候,阀片开始回落。当阀片回落至与阀座处,与阀座发生碰撞并产生微小的回弹,最终与阀座贴合,排气阀关闭。同时图3还反映出第2阶和第3阶振型对阀片上阀孔中心所对应点的位移影响很小,并且随着振型的阶次越高,该阶振型对排气阀阀孔中心点的位移影响越小,故在研究阀片运动工作特性的时候取一阶振型便可以满足要求。
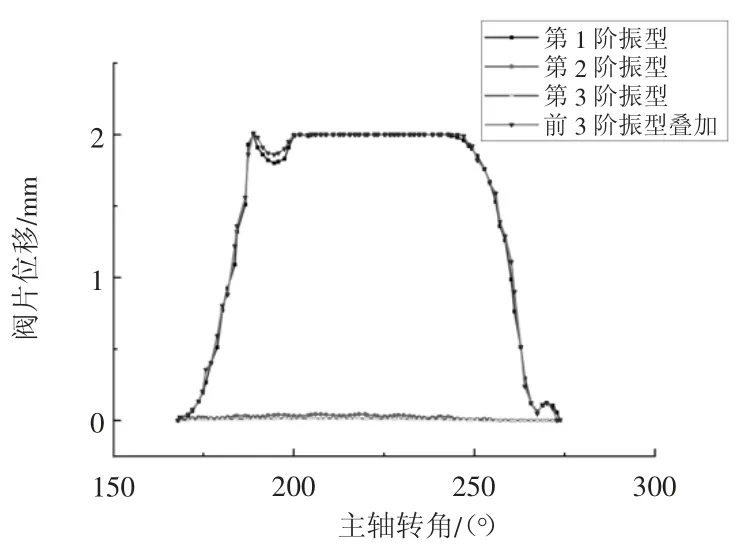
图3 模型求解结果
3 排气阀结构参数对舌簧阀工作特性的影响
3.1 升程对舌簧阀运动特性影响
在排气阀工作过程中,升程限位器高度不仅影响排气过程中工质的有效流通面积,还决定着阀片运动变化曲线,下面探究不同升程下阀片的运动规律。
从图4可以看出,不同的升程对阀片开启时的位移影响很小,阀片开启角一致。随着升程增加,阀片在与升程限位器碰撞后的反弹位移越来越大。当H=4 mm时,阀片碰撞升程限位器后便反弹回落,难以再次上升与升程限位器贴合。其原因在于,随着升程的变大,阀片与升程限位器碰撞时,阀片弯曲变形增加,弹性力增大,且碰撞时速度增大,造成碰撞后的反弹力增加,当气体力不足以克服弹性力和碰撞后的反弹力时,阀片便难以继续上升与升程限位器贴合。并且随着升程增大,阀片关闭角在减小,这是因为阀片与升程限位器接触时间越短,阀片回落速度越大,造成排气阀的提前关闭。但是过小的升程会导致阀片回落延迟,造成延迟关闭的现象。延迟关闭会引起气体倒流,压力损失增大。故在排气阀的升程高度选取上,应选择合适的升程。
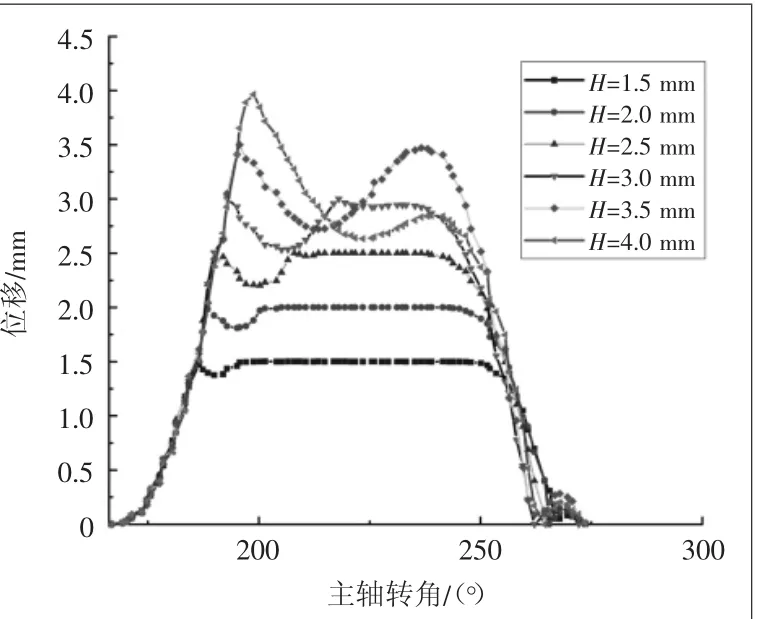
图4 阀孔中心点对应位移随不同升程的变化曲线
由图5可知,阀片处于上升状态时速度为正,下落状态时速度为负。在排气阀工作过程中,排气阀开启时,不同升程下阀片速度大致相同,阀片在气体力的作用下速度不断增加,当阀片上升到与升程限位器接触发生碰撞时,阀片速度方向瞬时变为负值,在气体力的作用下继续阀片速度继续增加,直到与升程限位器再次接触时再次变为负值,随后阀片速度会在0值附近波动且波动越来越小,直至阀片完全贴合在升程限位器上时,阀片速度变为0。阀片与升程限位器碰撞时速度随着升程增大而增大,阀片与升程限位器碰撞时的冲击力越大,而过大的碰撞速度会导致阀片的冲击破坏,故设计阀片时,应使阀片与限位器的碰撞速度在安全范围内。

图5 不同升程下阀片速度变化曲线
3.2 阀孔直径对舌簧阀运动特性影响分析
舌簧阀的有效流通面积和流量系数直接影响着涡旋压缩机的工作效率,而舌簧阀的有效流通面积跟舌簧阀的阀孔直径密切相关。当升程限位器高度为2.5 mm时,阀孔直径对舌簧阀位移的影响如图6所示,可以看出随着阀控直径变小,舌簧阀在排气过程中会出现延迟开启和延迟关闭的现象。当阀孔直径小于2.5 mm时,阀片不能及时开启和关闭,且阀片全开期变短。关闭延迟时,会导致气体回流,从而增加压力损失。
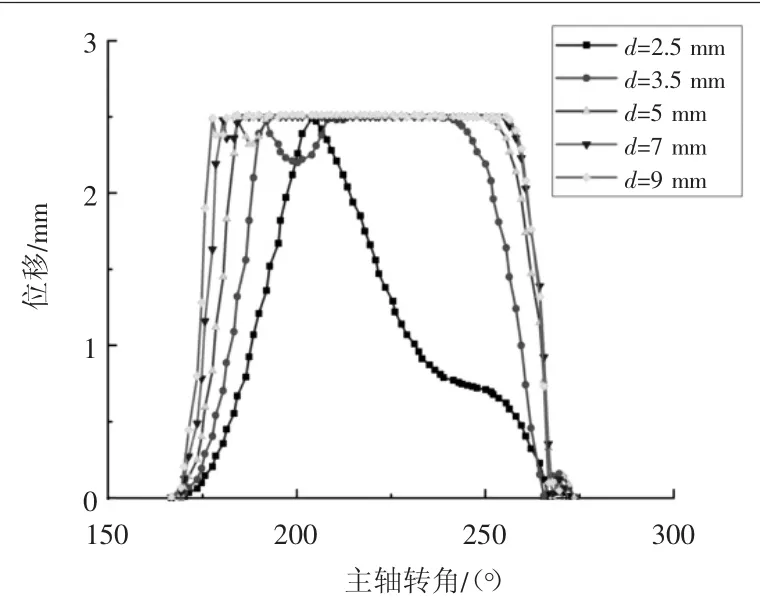
图6 阀孔中心点对应位移随阀孔直径的变化曲线
由图7可知,随着阀孔直径的变大,阀片在工作中的速度波动越大,当阀孔直径大于7 mm时,阀片在与限位器碰撞之后速度波动比较大,当阀孔直径小于3.5 mm时,阀片在排气过程中的全开时间变短,会导致排气效率下降。随着阀孔直径变大,阀片与限位器碰撞时的速度也越来越大,过大的阀孔直径会导致在排气阀全开过程中,阀片无法与限位器贴合而发生震颤现象。过小的阀孔直径会导致上升过程中速度过小,以至于阀片无法与限位器贴合,因此在设计阀孔的时候,尽量避免选择过大或者过小的阀孔直径,从而避免震颤现象和提高阀片工作效率。

图7 不同阀孔直径下阀片速度变化曲线
4 结论
本文基于薄板横向振动理论建立舌簧阀的数学模型,并在获取振型函数时把阀片看作悬臂薄板来获取,分析了前三阶振型对阀片上阀孔中心所对应点的位移情况,并研究了升程和阀孔直径对舌簧阀运动特性的影响,结果表明:1)随着振型的阶次越高,该阶振型对阀片上阀孔中心所对应点的位移影响越小,故在研究阀片运动工作特性的时候取一阶振型便可以满足要求;2)随着升程增大,阀片与升程限位器贴合时间变短,阀片会出现延迟关闭的情况且阀片与升程限位器的撞击速度变大;3)排气阀阀孔越小,有效流通面积和气体推力减小,阀片的开启和关闭都会延迟,阀孔过大会导致阀片与限位器碰撞时的速度过大,使得阀片无法与限位器贴合而产生震颤现象。
该研究结果有利于探究舌簧阀参数对于排气阀工作过程中的影响,避免阀片在工作过程中的提前开启和延迟关闭,以及阀片和限位器碰撞时产生的震颤现象,从而提升压缩机的效率,为涡旋压缩机舌簧阀的优化设计和实验提供理论基础。

