钢结构悬臂梁初始裂纹发展有限元动态仿真分析

鲁福全 王雪 裴坤 陈炳言 伊浩 张天成

（安徽建筑大学土木工程学院，安徽 合肥 230601）

0 引言

作为一种常用的建筑结构，钢结构在建筑工程中应用广泛。在计算机技术发展的推动下，有限元算法逐渐在建筑工程中得到应用，并形成了对钢结构进行研究的重要手段[1-2]。ABAQUS 在对材料进行非线性分析的问题上展现出了巨大的优越性[3]。本文以钢结构悬臂梁作为研究对象，对其初始裂纹进行有限元仿真分析。

1 钢结构悬臂梁损伤塑性模型

ABAQUS 在钢结构悬臂梁的分析工作中表现优越，钢结构悬臂梁损伤塑性模型常用于动态仿真中，通过各向同性损伤以及非关联塑性的方式对钢材料出现的无法恢复的损伤进行了有效的描述。

金属构件受压变形时，其内部形成众多细小滑移和损伤裂痕,简单地简化为几条裂痕而采用断裂力学方法研究是不可取的。钢材料受到外力时内部会产生细小裂痕和细微空腔。损伤力学适宜研究金属构件受外力时产生损伤的发展和演变。

损伤塑性模块是ABAQUS 的分析模块之一。该模块在金属构件分析中引入损伤指标，有效地模仿钢材拉伸引发强度因损伤增加而降低的特点，适用于钢结构的非线性分析。

ABAQUS 提供的钢结构损伤塑性模型是依据Kachanov，Raboinov，Lemaitre[4-7]等人提出的损伤塑性理论确定的，采用设定连续性参变量的方法，分析构件中损伤演化的复杂进程。

2 模型材料与工程概念

初始损伤对应于材料开始退化，当应力或应变满足于定义的初始临界损伤准则，则此时退化开始。ABAQUS 中 ，Damage of traction separation laws 中 包括 ：Quade Damage、Maxe Damage、Quads Damage、Maxs Damage、Maxpe Damage、Maxps Damage 6 种初始损伤准则。其中前四种用于一般复合材料分层模拟，后两种主要在扩展有限元法模拟不连续体问题时使用。此处，选用Maxps Damage 初始损伤准则进行模拟。模型材料设置如表1所示。

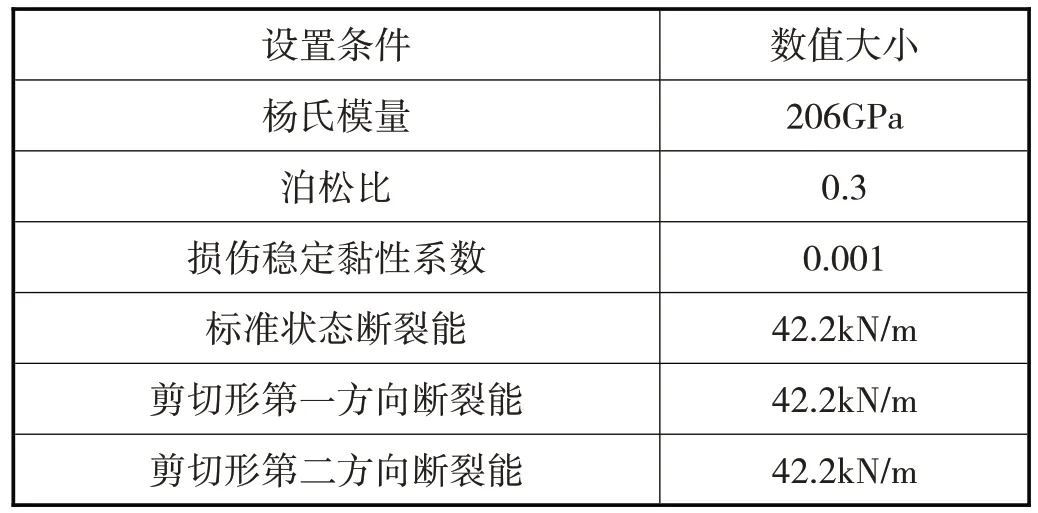
表1 模型材料设置

3 有限元仿真分析

由于篇幅有限，模型建立的过程仅进行简要说明，对Assembly模块、Step模块、Mesh模块未进行说明。

3.1 Part模块：基本建模

构建一个三维实体模型Cantileverbeam 与一个三维壳模型Crack（壳模型Crack 旨在插入实体模型Cantileverbeam中以作为悬臂梁裂缝参与仿真计算），其中，实体模型Cantileverbeam 在X-Y-Z 方向上的尺寸为10×3×2，壳模型Crack 在 X-Y-Z 方向上的尺寸为2×0×0.2。

3.2 Property模块：指派材料

创建实体模型Cantileverbeam 与壳模型Crack 的材料，并对相关部件进行材料指派。相关材料参数（如：杨氏模量、泊松比、损伤稳定黏性系数等）在模型材料与工程概念中已经阐明，此处不再赘述。

3.3 Interaction模块：设置裂纹

经Assembly 模块、壳模型Crack 插入实体模型Cantileverbeam上侧距左端1m处。

创建裂纹，并指派壳模型Crack 为实体模型Cantileverbeam的裂纹。

3.4 load模块：添加荷载

对悬臂梁施加荷载，并创建边界条件：该悬臂梁左端完全固定，右端自由，上侧受均布载荷作用100GPa，壳模型Crack 插入实体模型Cantileverbeam 上侧距左端1m 处，以作为悬臂梁裂缝参与仿真计算。完成建模的悬臂梁初始裂纹发展模型见图1所示。

4 仿真模拟结果

提交作业，得到5 个Step，由于Step1 变形不明显，只取钢结构悬臂梁的应力云图Step2～Step5。不同Step下（T2=0.200、T3=0.350、T4=0.575、T5=0.700）的应力云图如图2所示。

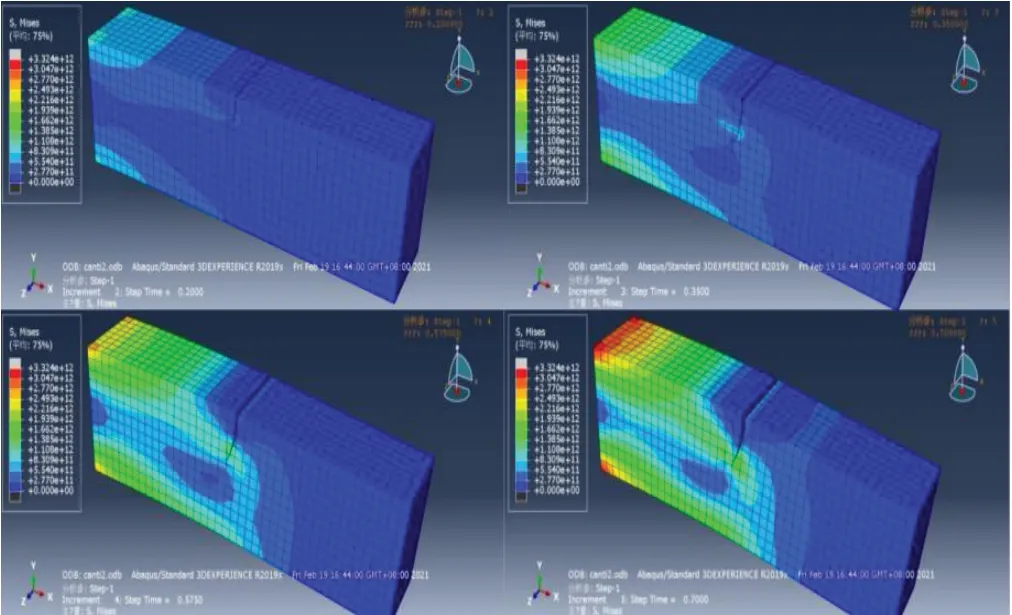
图2 不同Step下的应力云图

由图2中不同Step下的应力云图分析可知：

（1）对于悬臂梁的左端（根据模型实例，习惯上称悬臂梁受约束端方向为左，自由端方向为右，下同），其四脚周围出现了应力集中的现象。

（2）裂纹右下侧的应力普遍大于裂纹的左上侧的应力，且应力数值在裂纹处发生突变，数学上可以理解为函数在间断点（即裂纹处）发生了跳跃。

（3）裂纹左侧应力仍然较大，裂纹右侧应力普遍较小，可以判定，裂纹左侧大部分仍处于工作状态，裂纹右侧大部分已退出工作。

5 裂纹处应力分析

在钢结构悬臂梁受压变形中，为对悬臂梁裂纹处的应力状态有更为清楚的了解，对悬臂梁裂纹处在受压过程中的应力变化进行分析。

由于该模型荷载为均布荷载，且悬臂梁模型具有对称性。故对于相同位置、不同深度的单元，其应力状态相同。选取悬臂梁侧面裂纹附近的8 个单元进行应力分析，其中4 个为裂纹左侧单元，另4 个单元为裂纹右侧单元，钢结构悬臂梁裂纹处应力分析选中的单元如图3所示。

图3 钢结构悬臂梁裂纹处应力分析选中的单元

5.1 裂纹左侧单元应力分析

利用XY 数据，绘制裂纹左侧单元分析应力-时间变化曲线，如图4所示。

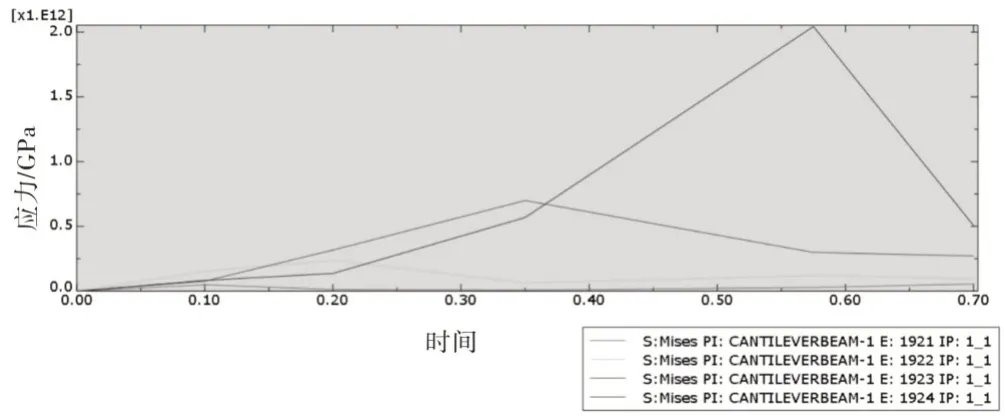
图4 裂纹左侧单元分析应力-时间变化曲线

由图像分析知：在钢结构悬臂梁上侧因均布荷载受压弯曲时：

（1）对于裂纹左侧部分，下部单元应力普遍大于上部应力；

（2）裂纹的出现导致左侧部分应力减小。对于裂纹左侧部分的应力大小，当单元右侧出现裂纹时，单元右侧部分将对该单元丧失力的作用，单元应力骤减，致使裂纹左侧部分应力随时间增大而呈现出先增大后减小的趋势；由图像可知E1921、E1922、E1923、E1924 右侧出现裂纹的分步时间分别为：T1=0.10、T2=0.20、T3=0.35、T4∈[0.55,0.60]。

（3）上部应力峰值出现的时间早于下部分。对于裂纹左侧部分，由于裂纹随时间增大而延伸，故下部裂纹出现时间迟于上部，致使上部分应力峰值出现的时间早于下部分。

5.2 裂纹右侧单元应力分析

利用XY 数据，绘制裂纹右侧单元分析应力-时间变化曲线，如图5所示。

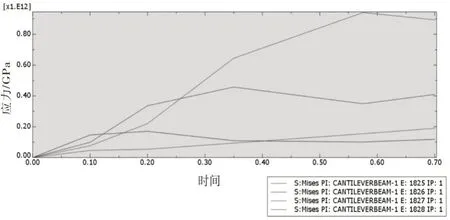
图5 裂纹右侧单元分析应力-时间变化曲线

由图5 可知，钢结构悬臂梁上侧在均布荷载受压弯曲时：

（1）对于裂纹右侧部分，下部单元应力普遍大于上部应力；

（2）与裂纹左侧不同，裂纹的出现对裂纹右侧应力大小的改变程度不及对左侧的改变：由5.1 节知，在裂纹延伸至下一单元的分步时间时（即为T1、T2、T3、T4），裂纹右侧E1825、E1826、E1827、E1828的应力大小下降较小，且后阶段并未继续下降，并没有出现裂纹左侧连续下降呈现极值的现象。

6 结束语

本文利用ABAQUS 对钢结构悬臂梁进行分析，建立了ABAQUS钢结构悬臂梁均布荷载下初始裂纹发展动态模型，并对裂纹处的应力状态进行了分析。结果表明，裂纹发展过程中存在以几种情况：

（1）下部单元应力普遍大于上部应力。

（2）约束端周围随时间增加出现应力集中的现象。

（3）裂纹约束端一侧上部应力峰值出现的时间早于下部分。

（4）裂纹自由端一侧的应力普遍大于裂纹约束端一侧的应力，且应力数值在裂纹处发生突变。

（5）裂纹两侧应力的大小、变化趋势是不同的，裂纹的出现对裂纹约束端一侧影响较大，对自由端一侧影响较小。