高速列车经过双线隧道瞬变压力及压力梯度特征

杜建明 房倩† 王赶 张顺金

（1.北京交通大学隧道及地下工程教育部工程研究中心，北京 100044；2.中国城市建设研究院有限公司，北京 100120）

高速列车突入隧道引起周围空气快速流动，因受到隧道壁面与车体表面限制而被瞬间挤压导致空气压力突变，从而在隧道内产生瞬变压力波。压力波随列车行驶不断产生并传播，同时以声速在隧道内壁、车体外壁、隧洞进出口等位置间连续反射、叠加和激发，最终在隧道内形成复杂的压力波系［1］。在作用于隧道壁面瞬变压力循环作用下（压缩波产生的压力与膨胀波产生的拉力），衬砌结构原生裂纹持续发展、交会与贯通，进而演化成宏观裂缝，从而使得衬砌结构完整性破坏、承载力降低、服役寿命缩短。隧道壁面瞬变压力时空特征及其梯度变化规律是衬砌结构动力响应分析的基础，相关研究已引起广泛关注。

高速列车经过双线隧道诱发气动特征的研究方法主要有现场实测［2-5］、动模型试验［6-9］和数值仿真［10-14］3 种方法。在现场实测方面，Ko 等［2］分析了列车速度与隧道断面对瞬变压力特征的影响规律，发现瞬变压力随断面增加而减低；瞬变压力最大正峰值近似与列车速度平方成正比；何德华等［3］分析了列车长度对瞬变压力波特征的影响规律，发现压力波动随列车长度增加而增加，其主要原因是列车进入隧道过程中车体表面摩擦效应引起压力变化所致。Liu 等［5］分析了隧道内单车经过与双车交会对瞬变压力的影响规律，发现双车交会对瞬变压力峰值影响显著，双车在隧道中断面交会位置也是最大峰值压力出现位置。在动模型试验方面，宋军浩等［8］分析了车头流线形长度对瞬变压力特征的影响规律，发现隧道壁面瞬变压力波动幅值随车头流线形长度增加而减小；Zhang等［9］分析了列车速度对瞬变压力特征的影响规律，发现瞬变压力幅值与列车速度平方近似成正比。在数值仿真方面，Li 等［10］分析了列车速度对瞬变压力特征的影响规律，发现隧道壁面瞬变压力幅值与列车速度平方近似成正比；骆建军［12］分析了海拔高度与温度对瞬变压力特征的影响规律，发现瞬变压力峰值随海拔高度与温度升高而降低；Niu 等［13］等分析了列车数量对瞬变压力特征的影响规律，发现瞬变压力峰值随列车数量增加而增加。上述研究成果极大加深了高速列车经过双线隧道诱发气动特征变化的相关认识。

隧道衬砌结构在瞬变压力作用下的动力响应分析中，瞬变压力峰值与压力梯度共同决定了衬砌结构的动力响应机制。例如，梅元贵等［15］通过数值仿真分析了隧道开孔缓冲结构长度、开口率等结构参数对初始压缩波强度及压力梯度的影响规律；闫亚光等［16］基于气动声学理论对洞口缓冲结构的横断面积函数、入口断面积及长度进行优化分析，发现隧道内初始压力波梯度峰值随缓冲结构长度增加而减小。目前，既有文献主要研究隧道洞口缓冲结构参数对初始压力波梯度的影响规律，有关车隧参数对瞬变压力梯度峰值的影响规律还未被全面研究。构建车隧参数与瞬变压力梯度之间的关系，结合瞬变压力作用下隧道衬砌损伤发展，从而建立车隧参数与衬砌损伤发展之间的内在联系，可用于直接指导我国高速列车在隧道内的安全运营。

为此，文章针对高速列车经过双线隧道诱发的气动特征变化，基于缩尺1∶1 的8 节编组列车构建隧道-列车-空气三维数值计算模型，在利用现场实测结果验证数值方法准确性的基础上，分析了隧道壁面瞬变压力时空特征，并进一步研究了列车速度、车隧阻塞比、列车数量以及双车等速交会对隧道纵轴中断面瞬变压力及压力梯度特征的影响规律。

1 计算模型

1.1 几何模型

列车模型为我国高速铁路普遍采用的CRH380型动车组，建立缩尺1∶1 的8 节编组动车，车宽与车高分别为3.38 m 与3.70 m，车身断面积为11.22 m2，车头流线形长度为12.0 m，如图1所示。

图1 高速列车模型Fig.1 High-speed train model

隧道模型为我国标准的双线隧道，净空断面积100 m2，双线间距5.0 m，车隧阻塞比0.112 2。根据田红旗［1］所提式（1）可得8 节编组列车以350 km/h 单车经过双线隧道的最不利隧道长度为912.8 m，为便于模型构建，隧道长度取1 000 m，计算模型整体布置如图2所示。列车鼻尖距隧道洞口50 m，车底距地面高度0.2 m。

图2 计算模型整体布置（单位：m）Fig.2 Overall layout of calculation model（Unit：m）

式中，LTU为最不利隧道长度，Ma为马赫数（0.286），LTR为列车长度（203 m）。

1.2 模型网格

采用结构化网格技术对整个计算模型进行网格划分，列车车头与隧道洞口模型网格如图3 所示。为保证计算结果精度，对列车车头、车尾以及隧道近壁面区域进行网格加密，隧道与列车模型最小网格尺寸分别为0.01 m 与0.007 5 m，模型网格总数为1.679×107。

图3 模型网格Fig.3 Model mesh

1.3 边界条件与测点布置

计算模型边界条件与压力测点布置如图4所示。结合滑移网格技术［17-18］将整个计算模型划分为静止域与移动域，通过在两个域之间设置接触面（Interface）来实现列车与隧道之间的相对运动。压力测点布置在隧道壁面，横断面内共布置7个测点，1号至3号测点位于近列车壁面，距地面高度分别为1.5、3.0和5.0 m；4号测点位于拱顶，距地面高度8.9 m；5号至7号测点与3号至1号测点对称于隧道中线。隧道纵向共布置19个监测断面，以与隧道入口之间的距离表示监测断面所在位置，如X=0.2 km表示距隧道入口0.2 km的横向监测断面。限于篇幅，文章主要选取典型测点压力数据进行分析。

图4 计算模型边界条件与压力测点布置Fig.4 Boundary condition of calculation model and layout of pressure monitoring point

1.4 求解方案

采用基于有限体积法的商业软件ANSYS FLUENT 进行数值计算，湍流模型采用RNGk-ε模型；压力场与速度场之间的耦合采用SIMPLE算法；对流项与扩散项采用二阶迎风格式；非定常项采用二阶隐式格式。所有数值计算时间步长设为0.001 s，每个时间步长内迭代次数设为50次。

2 数值方法验证

为了验证文章所用数值方法的可靠性，将数值计算结果与京沪高铁某隧道现场实测结果进行对比分析。该隧道为典型的单洞双线隧道，隧道长度978 m，列车试验速度300 km/h［19］。数值计算所用隧道及列车模型与现场实测保持一致。瞬变压力测点位于轨面高度1.5 m 的近列车壁面。数值计算与现场实测结果对比如图5所示。可知，数值计算与现场实测的瞬变压力时程曲线变化规律基本相似，吻合度良好。距隧道入口500 m 测点的正负压力峰值相差3.27%与1.42%；距隧道入口860 m 测点的正负压力峰值相差1.44%与1.57%，均在工程允许误差范围（±10%）之内［20］。故可认为文章所用数值方法及其计算结果是合理可靠的。

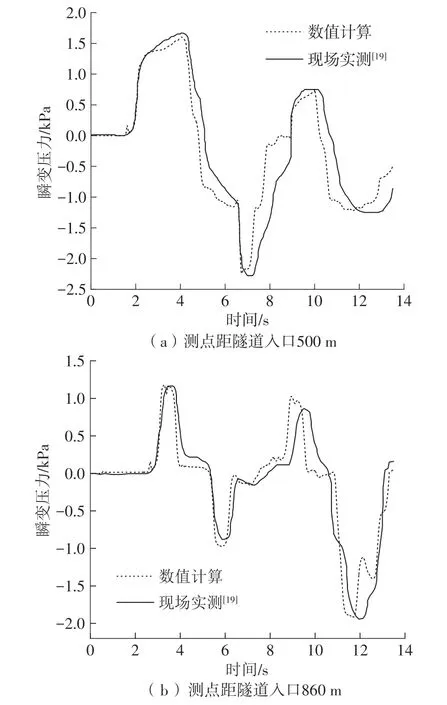
图5 数值计算与现场实测结果对比Fig.5 Results comparison between numerical calculation and field measuring

3 隧道壁面瞬变压力时空特征

3.1 瞬变压力波系及时程曲线

图6为列车通过隧道的运行轨迹及其诱发的压力波与隧道壁面瞬变压力之间的对应关系。其中，对图6（a）而言，实线（N）与虚线（T）分别代表列车车头与车尾在隧道内部的运行轨迹；实线（C1、C2、C3、C4和C5）与虚线（E1、E2、E3和E4）分别代表压缩波与膨胀波在隧道内部的传播轨迹；水平实线（M）代表隧道壁面监测断面所在的纵轴位置，即X=0.5 km；压力波以声速（340 m/s）在隧道内传播，是车速（97.22 m/s）的3.5倍。列车车头突入隧道入口诱发压缩波C1，C1 到达监测断面引起瞬变压力首次升高；车尾突入诱发膨胀波E1，E1 先于车头到达监测断面，引起瞬变压力首次降低；C1到达出口时，部分以微压波形式向四周辐射，部分以膨胀波形式E2 重新反射回隧道；E2 先于车头到达监测断面，引起瞬变压力降低；待车头到达时，瞬变压力持续降低；E1 在出口反射形成的压缩波C2 到达时，瞬变压力第二次升高；待车尾以及E2在入口反射形成的压缩波C3 顺序到达后，瞬变压力持续升高；待C2在入口反射形成的膨胀波E3到达时，瞬变压力第二次降低；待C3 在出口反射形成的膨胀波E4 到达时，瞬变压力持续降低；待车头突出隧道出口诱发的压缩波CI到达时，瞬变压力第三次升高；待E3 在出口反射形成的压缩波C4到达时，瞬变压力持续升高。综上可知，列车与压力波到达监测断面的时刻基本能够反应壁面瞬变压力的变化趋势，即压缩波与车尾到达监测断面时引起瞬变压力升高，膨胀波与车头到达时引起瞬变压力降低。

图6 隧道内列车运行轨迹及其诱发的压力波与壁面瞬变压力之间的对应关系Fig.6 Relationship between train path and induced pressure waves inside tunnel and transient pressure of tunnel wall

3.2 瞬变压力纵断面分布

图7 为3 号测点在隧道纵轴不同位置的瞬变压力时程曲线。从图7可知，隧道纵轴不同位置测点的瞬变压力时程曲线变化规律基本相似，即升高-降低周期性变化。但对每一个测点而言，瞬变压力峰值、压力梯度以及到达峰值压力所需时间又表现出显著差异，其主要原因是压力波到达测点的时刻差异以及携带能量高低所致。列车突出隧道出口会再次诱发压缩波与膨胀波，并以声速向隧道内反射传播，从而导致近出口壁面测点的瞬变压力峰值增大，如X=0.85 km测点的负压峰值显著大于近入口壁面测点X=0.15 km。图8为3个典型压力峰值（最大正峰值、负峰值与峰峰值）沿隧道纵轴分布曲线。可知，3 个典型压力峰值沿隧道纵轴方向随着测点位置不同而显著变化，主要表现为近洞口附近的3个典型压力峰值普遍小于隧道中部附近。

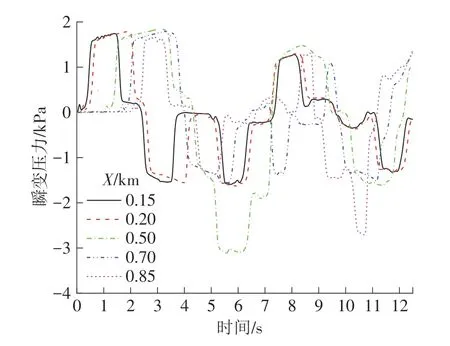
图7 3号测点在隧道纵轴不同位置的瞬变压力时程曲线Fig.7 Transient pressure time-history curves of different loca⁃tions of tunnel longitudinal axis for measuring point 3

图8 3号测点的3个典型压力峰值沿隧道纵轴分布Fig.8 Distribution of three typical pressure peaks along tunnel longitudinal axis for measuring point 3

3.3 瞬变压力横断面分布

隧道纵轴不同位置横断面测点的瞬变压力时程曲线如图9所示。可知：当列车车头到达监测断面前，壁面测点瞬变压力幅值主要由洞内压力波强度决定，同一横断面内不同测点瞬变压力时程曲线基本重叠；当车头与车尾先后经过监测断面时，由于列车偏心效应导致车体两侧的空气受压体积不同，从而使得同一横断面内不同测点瞬变压力表现出一定的差异性，但最大压力差分别仅0.044 kPa（X=0.50 km）与0.021 kPa（X=0.85 km）；当车尾经过监测断面后，受列车尾流效应［21］影响，同一横断面内不同测点瞬变压力时程曲线表现出轻微振荡；随着车尾与监测断面之间距离的增加，列车尾流效应的影响逐渐减弱，同一横断面内不同测点瞬变压力时程曲线再次重叠。

图9 隧道横断面测点瞬变压力时程曲线Fig.9 Transient pressure time-history curves of monitoring points of tunnel cross-section

4 隧道壁面瞬变压力特征影响因素分析

通过控制变量的方法进一步对列车速度、车隧阻塞比、列车数量以及双车等速交会对隧道壁面瞬变压力与压力梯度的影响规律进行探究。瞬变压力横断面分布特征分析表明，横断面内瞬变压力分布均匀、差异较小。故以下章节选取近列车壁面的3 号测点压力数据进行分析。

4.1 列车速度的影响

铁路列车速度的提高是隧道气动效应诱发的重要因素之一，为此，研究车速对瞬变压力及其梯度特征的影响规律。列车速度为300、350和400 km/h时，典型压力峰值沿隧道纵轴分布如图10 所示。可知，隧道纵轴中断面瞬变压力峰值普遍大于洞口段。图11 为不同列车速度时隧道纵轴中断面瞬变压力与压力梯度时程曲线。可知，随着列车速度的增大，瞬变压力与压力梯度正负峰值显著增加，且到达峰值所需时间逐渐减少。列车在隧道内高速挤压空气产生压力波，压力波所携能量随车速增大而增大，从而导致瞬变压力增速更快、峰值更高。相比较低车速的列车，车速更高的列车诱发的入口压力波更早在隧道内传播，从而使得到达压力峰值所需时间更短。进一步对3个典型压力峰值以及初始压力梯度正峰值与列车速度之间的关系进行拟合，发现3 个典型压力峰值与列车速度平方成线性关系，相关系数R2大于0.99，初始瞬变压力梯度正峰值与列车速度3次方成线性关系，相关系数R2大于0.99，如图12所示。

图10 不同列车速度时典型压力峰值沿隧道纵轴分布Fig.10 Distribution of typical pressure peaks for different train speeds along tunnel longitudinal axis

图11 不同列车速度时瞬变压力与压力梯度时程曲线（X=0.5 km）Fig.11 Time-history curves of transient pressure and pressure gradient for different train speeds（X=0.5 km）

图12 列车速度与典型压力峰值及初始压力梯度正峰值之间的关系（X=0.5 km）Fig.12 Relationship between train speed and typical pressure peaks and positive peak of initial pressure gradient（X=0.5 km）

4.2 车隧阻塞比的影响

既有高铁隧道可采用套衬来解决衬砌开裂或渗漏水病害，未来也可通过扩建隧道断面来降低气动负面影响，此时，车隧阻塞比随之改变。为此，研究车隧阻塞比对瞬变压力及其梯度特征的影响规律。列车车型保持不变，通过扩大隧道净空断面积来模拟不同车隧阻塞比的情况。车隧阻塞比为0.080 1，0.093 5 和0.112 2 时，典型压力峰值沿隧道纵轴分布如图13 所示。可知，不同车隧阻塞比时，典型压力峰值沿隧道纵轴分布特征基本相似，隧道纵轴中断面瞬变压力峰值普遍大于洞口段。图14 为不同车隧阻塞比时隧道纵轴中断面瞬变压力与压力梯度时程曲线。其中，图14（a）与图14（b）中“+1/2/3”分别表示瞬变压力第1/2/3 次升高与压力梯度第1/2/3次正峰值，“-”意义正好相反。可知，不同车隧阻塞比时瞬变压力与压力梯度时程曲线变化规律基本相似，瞬变压力与压力梯度正负峰值随车隧阻塞比增大而增大。车隧阻塞比越大，列车在隧道内行驶过程中受压空气体积越小，导致瞬变压力与压力梯度越大。进一步对3个典型压力峰值以及压力梯度峰值与车隧阻塞比之间的关系进行拟合，拟合结果如图15所示。发现3个典型压力峰值与车隧阻塞比的平方成线性关系，相关系数R2大于0.99，压力梯度正负峰值与车隧阻塞比的幂次方（2.51～3.14）成线性关系，相关系数R2大于0.99。

图13 不同车隧阻塞比时典型压力峰值沿隧道纵轴分布Fig.13 Distribution of typical pressure peaks for different blockage ratios along tunnel longitudinal axis

图14 不同车隧阻塞比时瞬变压力与压力梯度时程曲线（X=0.5 km）Fig.14 Time-history curves of transient pressure and pressure gradient for different blockage ratios（X=0.5 km）

图15 车隧阻塞比与典型压力峰值及压力梯度峰值之间的关系（X=0.5 km）Fig.15 Relationship between blockage ratio and typical pres⁃sure peaks and pressure gradient peaks（X=0.5 km）

4.3 列车数量的影响

为了进一步明确短列车（4 车）代替原型车（8车）研究隧道壁面瞬变压力及其梯度特征方法的合理性与准确性。对不同列车数量下的瞬变压力及其梯度特征变化规律展开研究。列车数量为4 车、6 车和8 车时，典型压力峰值沿隧道纵轴分布如图16 所示。从图16 可知，列车数量为8 车时对应的瞬变压力负峰值与峰峰值沿隧道纵轴分布特征显著区别于其它列车数量（4 车和6 车），但不同列车数量的隧道纵轴中断面瞬变压力峰值普遍大于洞口段。图17 为不同列车数量时隧道纵轴中断面瞬变压力与压力梯度时程曲线。从图17 可知，不同列车数量时瞬变压力时程曲线变化规律基本相似，但峰值压力与到达峰值压力所需时间存在差异。如t=1.8～3.4 s时间段，列车车身进入隧道引起摩擦效应［22］导致的瞬变压力峰值随列车数量增加而增大。当列车数量从4 车增加到8 车时，瞬变压力峰值增幅9.5%。不同列车数量时压力梯度时程曲线差异显著，主要表现为到达压力梯度峰值所需时间存在延迟。如t=2.4～3.5 s 与t=5.3～7.4 s 时间段，到达压力梯度峰值所需时间随列车数量增加而延迟。如t=7.4 s，列车数量为8车时对应的压力梯度正峰值显著区别于其它列车数量（4 车～7车）。进一步对3 个典型压力峰值与列车数量之间的关系进行拟合，拟合结果如图18 所示，发现3个典型压力峰值与列车数量之间的关系可用指数函数表达，相关系数R2大于0.99。综上可知，在研究隧道壁面瞬变压力时空特征时，应谨慎对待采用短列车（4 车）代替原型车（8 车）的方法，或者需对计算结果进行修正。

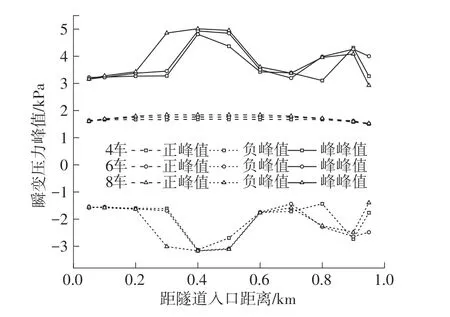
图16 不同列车数量时典型压力峰值沿隧道纵轴分布Fig.16 Distribution of typical pressure peaks for different num⁃ber of trains along tunnel longitudinal axis

图17 不同列车数量时瞬变压力与压力梯度时程曲线（X=0.5 km）Fig.17 Time-history curves of transient pressure and pressure gradient for different number of trains（X=0.5 km）

图18 列车数量与典型压力峰值之间的关系（X=0.5 km）Fig.18 Relationship between number of train and typical pres⁃sure peaks（X=0.5 km）

4.4 双车等速交会的影响

双车等速交会的数值实现与单车类似，具体实现方法可参考文献［17，19］。隧道内单车经过与双车等速交会时典型压力峰值沿隧道纵轴分布如图19所示。可知，隧道内双车等速交会诱发的瞬变压力峰值普遍大于单车经过，且隧道纵轴中断面瞬变压力峰值普遍大于洞口段。图20 为单车经过与双车等速交会时隧道纵轴中断面瞬变压力与压力梯度时程曲线。图中“+1/2/3”以及“-1/2/3”含义与图14 相似。从图20 可知，相比单车经过隧道，隧道内双车等速交会时瞬变压力与压力梯度峰值更大，其主要原因是双车等速交会诱发的压力波或膨胀波在隧道内以固定相位差进行叠加导致。进一步对3 个典型压力峰值进行分析，发现双车等速交会诱发的典型压力峰值普遍大于单车经过诱发的2倍，如图21 所示。如最大正负压力峰值，双车等速交会分别是单车经过的2.22 倍和1.15 倍。且双车等速交会时引起的压力梯度正负峰值普遍大于单车经过。双车等速交会时最大正负压力梯度峰值分别达到了27.8 kPa/s 与-23.9 kPa/s，分别是单车经过的1.87倍与2.03倍。

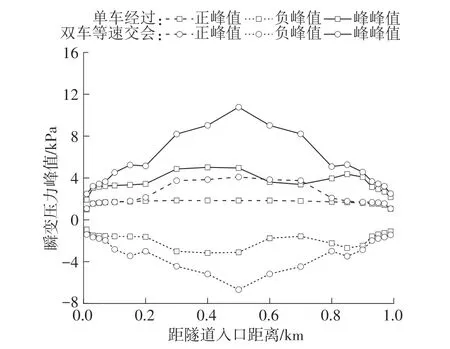
图19 单车经过与双车等速交会时典型压力峰值沿隧道纵轴分布Fig.19 Distribution of typical pressure peaks for single train passing by and two trains intersecting with the same speed along tunnel longitudinal axis

图20 单车经过与双车等速交会时瞬变压力与压力梯度时程曲线（X=0.5 km）Fig.20 Time-history curves of transient pressure and pressure gradient for single train passing by and two trains inter⁃secting with the same speed（X=0.5 km）

图21 单车经过与双车等速交会时典型压力峰值分布（X=0.5 km）Fig.21 Distribution of typical pressure peaks for single train passing by and two trains intersecting with the same speed（X=0.5 km）

5 结语

（1）隧道纵向不同截面瞬变压力时程曲线均表现出升高-降低周期性变化规律，同一横截面内瞬变压力时程曲线基本重叠。

（2）瞬变压力及其梯度正负峰值随车速或阻塞比增大而增加；典型压力峰值（正/负峰值、峰峰值）与车速或阻塞比平方成线性关系；初始压力梯度正峰值与车速3次方成线性关系，压力梯度正负峰值与阻塞比幂次方（2.51～3.14）成线性关系。

（3）瞬变压力及其梯度峰值到达时刻随列车数量增加而延迟。典型压力峰值与列车数量之间满足指数函数关系，8 车对应的压力梯度最大正峰值是其它列车数量（4～7 车）的1.25 倍，建议谨慎使用短列车（4 车）代替原型车（8 车）来研究隧道壁面瞬变压力时空特征。

（4）隧道内单车经过与双车等速交会诱发瞬变压力及其梯度时程曲线变化规律基本相似。双车交会最大的正/负压峰值分别是单车的2.22 与1.15 倍，最大压力梯度正/负峰值分别是1.87 与2.03 倍，故双车交会对隧道结构及附属设施影响更大。

（5）文章主要分析了车隧因素与隧道壁面瞬变压力及其梯度之间的关系，后续工作将研究瞬变压力及其梯度作用下隧道衬砌结构动力损伤，进而基于瞬变压力及其梯度中间变量来构建车隧因素与衬砌结构动力损伤之间的关系，最终为高铁隧道安全运营提供理论支撑。