楔形管壳式蓄热罐的传热性能

毛前军，陈凯莉

（武汉科技大学城市建设学院，湖北 武汉 430065）

在“碳达峰、碳中和”国家目标政策的积极推动下，可再生能源的兴起与发展对我国结构转换、动能转变、低碳转型具有重要意义。但是大多数可再生能源如太阳能、风能、潮汐能是间歇或循环能源，在时空尺度上供需不匹配，这就需要将储能系统与可再生能源结合使用，以确保其稳定运行。在储能技术中，采用相变材料(PCM)的潜热储能系统由于其性能稳定、储/放热温度波动小、储热密度大等特点成为学者们广泛研究的储热方式[1]。

然而，大多数相变材料的导热系数较低，使潜热蓄热系统存在热响应较慢、蓄热器工作效率达不到预期的问题，这限制了潜热存储器件的储热性能。因此，提高相变储热单元中相变材料与热源之间的换热性能是研究热点。根据传热方程，提高潜热储能系统热性能的主要途径有三种：增加传热面积[2-3]，提高导热系数[4-5]，通过混合PCM 材料改善熔化过程的均匀性[6-7]。在PCM 的熔化过程中自然对流的传热速率通常远高于热传导的传热速率[8]，所以强化相变储热单元中的自然对流能够有效提高系统储能效率。袁艳平等[9]数值模拟了在垂直热壁边界条件下，相变储能单元的熔化过程，通过对板式储能单元翻转来强化对流传热，研究了Ra数、Ste数和单元高宽比对翻转传热强化作用的影响。Kumar等[10]提出了一种新型的漏斗形结构的管壳式潜热储能罐，利用壳体表面的倾斜来实现PCM 更均匀地温度分布，从而提高系统的热性能。霍宇涛等[11]研究了内部管道位置、方腔倾斜角度对PCM 熔化过程的影响规律。结果表明内管道位置在偏上部时会受到自然对流阻碍作用，降低PCM 的熔化速率。但在此时倾斜方腔，会改变管道热流体到上部界面的距离，使熔化加快。除此之外，还有其他方式可以强化相变蓄热单元中的自然对流，如改变内流管的形状与偏心距[12]、改变相变单元的几何构造[13]、添加翅片[14]等方式。

本研究将在矩形储罐的基础上改进出一种新型几何结构的管壳式潜热蓄热装置，通过优化矩形结构来增强自然对流。依据传统矩形储热单元存在的熔化死角问题，利用楔形化、内流管偏心以及罐体倾斜以增强自然对流的方式进行改善，所得结论对相变蓄热装置的设计及优化具有指导意义。

1 模型描述

1.1 物理模型

以竖直放置的矩形管壳式相变储热单元作为基本结构，通过改变其几何外形来强化其中相变材料(PCM)熔化过程中的自然对流，达到加快相变材料熔化速度、减少熔化时间的目的。在本研究中，在保证PCM 体积一定的情况下，在基础模型矩形上改进为楔形，传热流体(HTF)放置在壳体中心的铜管内流动，PCM 储存在环形空间中，如图1所示。

图1 矩形与楔形储能罐尺寸Fig.1 Rectangular and wedge-shaped storage tank dimensions

标准矩形罐的单元尺寸为222 mm(长度)×222 mm(宽度)×350 mm(高度)，在此体积的基础上，楔形总高度为H，切体高度设为S，切体底面设为d，为50 mm。中心带有直径为25 mm 的铜管，管内流经358 K 的水为换热介质。测点1～7 分为上、中、下三层。顶层测点1、2、3 间距25 mm均匀布置在距罐体底座300 mm 处，中层测点4 布置在距底座200 mm 处，底层测点5、6、7间隔25 mm放置在距底座100 mm处。选用国药集团生产的低温切片石蜡作为相变材料，并进行热物性测试，密度与热导率取测温范围内的平均值，比热容在各个温度范围内变化较大，采用线性法保留所有测量值。动态黏度与热膨胀系数参考文献[15]，DSC曲线在253～363 K 温度范围内升温，计算得出相变潜热与固/液相温度，模拟参数设置如表1所示。

表1 石蜡热物理参数Table 1 Thermophysical parameters of paraffin wax

1.2 数学模型

数学模型被简化，只考虑PCM 和热流管外壁之间的传热行为。物理模型的假设如下：

（1）将熔化的PCM 视为不可压缩的流体，考虑相变域中的自然对流，只考虑温度变化引起的PCM 的密度变化，所以密度项设为Boussinesq 近似值。

（2）假设系统是绝热的。

（3）只考虑罐体内部的PCM 与内流管的导热与自然对流，忽略影响较小的热辐射行为。

（4）由于管程较短，忽略内流管中热水的轴向温度与径向温度变化[16]。

（5）在相变温度范围内，PCM 的热容量会发生突变，而其他热物理特性不会随着温度的变化而发生很大的变化。因此，假设PCM 的热容量是线性变化的，而其他热物理特性是各向同性的，不随温度变化。

综上所述，本案例的边界条件描述如下，HTF的入口边界：恒速和温度条件，v=5 L/min，Tin=358 K；HTF的出口边界：充分发展的条件，∂u/∂x=∂v/∂x=∂T/∂x=0；内管壁边界；无滑移速度和耦合壁条件，u=v=0；其他墙体边界：无滑移速度u=v=0和绝热边界：径向的q=kw∂T/∂r=0，轴向的q=kw∂T/∂x=0为初始条件，整个领域的温度被设定为306 K的统一值，并且整个领域的速度为0。热平衡方程是基于PCM 和热流管内壁之间的耦合传热而建立的。为了模拟固-液之间的相变，采用了焓-孔隙率法，并引入了液相分数ƒ来表示液相材料占总体积的比例，这反过来又可以表示熔化率和熔化相界面的位置。对于焓-孔隙率法，能量守恒的控制方程对于固相和液相是相同的，用总体积焓和温度来表示[17]：

由于密度变化较小，采用了Boussinesq 近似法，并根据参考密度(ρ0)和温度(T0)以及体积膨胀系数(β)进行建模。动量方程可以写成：

其中Amush是一个反映黏稠区形态的常数，描述了材料凝固时速度降低到零的陡峭程度，这个常数在104～107之间变化，本工作考虑105[18]。ε=0.001是一个小的计算常数，用于避免除以零。

连续方程为：

2 求解方法与模型验证

根据物理和数学模型，利用FLUENT软件建立三维模型。计算选择隐式、非稳态求解器求解，采用焓-多孔介质模型，并加载凝固/熔化模型、开启能量方程。计算域使用六面体网格进行离散化，压力和速度的耦合采用SΙMPLE算法，动量与能量方程采用一阶迎风格式离散，压力计算使用PRESTO。设置完成后进行试算石蜡在初始室温为306 K，HTF 的温度为358 K，流量为5 L/min 条件下的熔化过程。设置监视窗口对7个测点温度、PCM的平均温度及液相分数进行实时追踪并导出。如图2所示，经过试算，当网格数达到497979，时间步长为1 s时可满足计算精度要求。

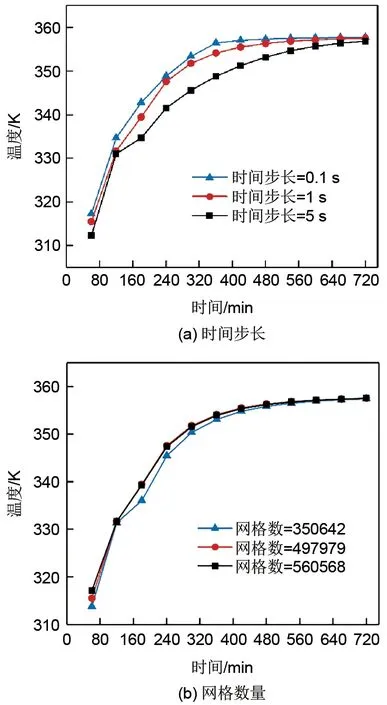
图2 时间步长及网格数量无关性验证Fig.2 Verification of the independence of the time step and the number of grids

为了验证传热模型的准确性，进行标准矩形储罐的实验研究，实验流程如图3所示。本实验中的矩形管壳式相变储热器是主要以4块2400 mm(长)×800 mm(宽)的太阳能集热板提供热源，结合温控装置与功率为1 kW 的电加热棒稳定温度的单罐储热系统。为了清晰观察PCM 的熔化特征，罐体外壳壁采用可视化良好的亚克力板(PMMA)材料，并包裹厚度为300 mm聚苯板保温，可以认为是完全绝热的。水箱是由1080 mm×1100 mm的不锈钢材料制成，内壁使用厚度为500 mm的聚氨酯发泡材料做保温处理。热水在水箱内达到358 K后，调整阀门，使涡轮流量计的示数稳定在5 L/min，在水泵的动力作用下使热水通入内流铜管进行实验。测点温度由K型热电偶传输，在常温下，其精度可达0.08 ℃。实验当天9 点室温为306 K，天气晴朗，假设设备运行不受太阳辐射的影响。

图3 实验系统流程图Fig.3 Experimental system flow chart

利用FLUKE 2638A数据记录仪记录下K型热电偶传输的测点温度数据与模拟数据进行拟合验证。避免偶然性带来的错误结论，取point 3、point 4和point 5 与模拟数据分别进行对比，以验证上述模型的可靠性。这三点不仅代表PCM 横切面上、中、下三层中各一点，也表示着纵切面距离换热管由近及远。如图4所示，实验值与模拟值一直吻合较好，但随着时间的推移实验值的温度低于模拟值的温度，这是由于实验观测需要，将保温层频繁地揭开追踪相界面的位置，致使系统有一定的热损失，并且室内温度波动也会造成一定的影响。但经计算实验结果与数值模拟吻合性较好，最大偏差不超过±3.5%，说明基于FLUENT软件的物理模型是可靠的，误差在可接受范围内。因此，该模型可用于其他被动传热的预测。

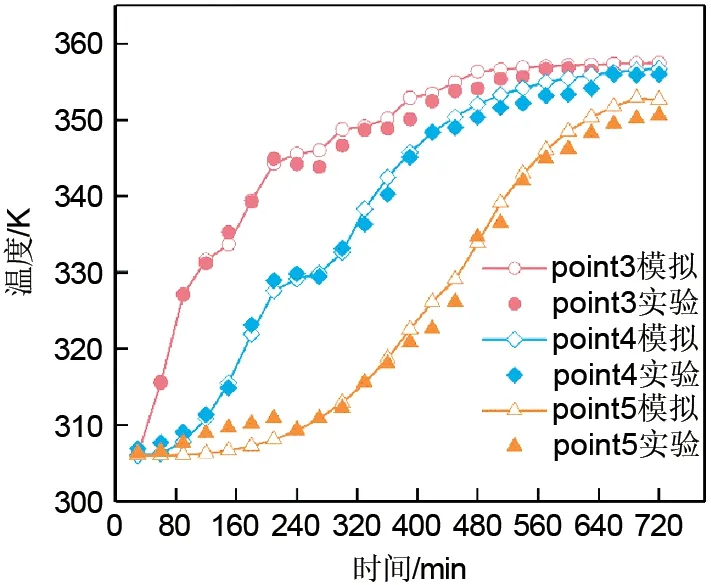
图4 模拟值与实验值的比较Fig.4 Comparison of simulated and experimental values

3 结果与讨论

3.1 罐体下部几何尺寸对熔化过程的影响

由于PCM 在矩形蓄热单元内的熔化速率由快到慢依次为上部＞左/右部＞下部[19]，故本工作将下部尺寸削减，以减轻各部分熔化速率不均造成的对蓄热效率的影响。选取切体高度S作为影响因素，将楔形比(X)定义为切体块高度(S)与切体块宽度(d)的比率，对不同楔形比模型进行数值模拟计算。表2表示了在不同的楔形比方案下，蓄热系统的详细尺寸及完全熔化时间的变化。其中“熔化时间缩短比率”定义为标准矩形罐(X=0)和不同楔形比的罐体内相变材料完全熔化时间的差值与标准矩形罐内相变材料完全熔化时间的比值。

表2 不同楔形比对蓄热单元的尺寸与效率影响Table 2 Effect of different wedge ratios on the size and efficiency of thermal storage units

由表2可知，在PCM体积相同的前提下，当X=5时，蓄热系统内PCM 的完全熔化时间最短，熔化时间缩短比率最高。由此证明，通过削减矩形下部壳体尺寸来改善系统底部蓄热速率过低的手段是有效的。这是由于PCM加热后温度升高，密度减小，在浮力作用下向上运动，使得壳体上部最先熔化，自然对流的环流由于重力的作用，只会形成一个向下的单向循环，从而在距离热流管最远的区域会形成一个难以流动和熔化的“死角”。而将“死角”区域削减后，改善了上下温度层分布的不均匀性，总熔化时间减少。

图5 从左至右展示了不同楔形比X，在t=180 min 换热管中心垂直面的温度分布云图。由图中可以看出随着切体高度S的增大，边角处的PCM 温度有所上升，到X=5 时罐体内温度分布最为均匀，但随着S的继续增加，到X=7时，罐体内出现了难以熔化的区域。这是因为当X由0增加到5时，在热传导的作用下，距离换热壁面近的PCM会最先升温熔化，故难熔区域会随着切体高度的增加而减少，升温速率加快。但是如果S过大，即当X=7时，虽然罐体边缘距离换热壁面会更近，但是一方面，PCM 加热后密度减小，在浮力作用下向上运动，高温液态PCM 在罐体上方聚集，且罐体整体高度增加，使其难以在重力的作用下向下流动传热；另一方面，液相石蜡的热阻随着几何尺寸的增大而增大，对传热的阻碍作用也增大，因此蓄热罐体的削减高度不能过大，X=5时的楔形罐具有最高传热效率。

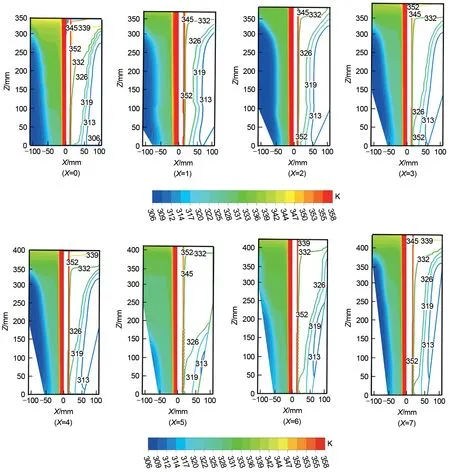
图5 不同楔形比的温度分布云图Fig.5 Cloud plot of temperature distribution for different wedge ratios

3.2 偏心距对熔化过程的影响

对于管壳式相变罐体来说，为了换热的均匀性，热流管一般放置在罐体的中心处。但是对于具有偏心圆管的楔形蓄热系统目前还鲜少涉及，图6展示了具有不同偏心距的热流管在蓄热过程中的储能量与储热速率的变化情况。将偏心距定义为I=D/C，其中D为圆管圆心到截面中心点的距离，C为截面中心到底边的距离。根据公式(9)与(10)计算储热量与储热速率，不同偏心距完全熔化时的储热量基本相同，但是在熔化时间与熔化速率上却有显著的差异。偏心距越大，即热流管越靠近储热罐体的壁面，系统的换热效率就越低。这是因为换热圆管偏心时，处于换热圆管与罐体壁面近侧的PCM 会在高温壁面的热传导作用下迅速升温熔化，而远侧PCM 厚度大于近侧PCM，通过热传导传热的速率较慢。当近侧的PCM 完全熔化成高温液态时，导热热阻增大，传热速率下降，并且在垂直向下的重力作用下，近侧的高温液态PCM 无法沿水平方向流向远侧。使得远侧较厚的固态PCM 无法与大范围的高温液态PCM 进行热接触，自然对流的效果也远不及近侧，整个蓄热系统的热响应被延长，蓄热效率也随之降低。因此偏心距会对楔形罐体熔化效率的提升起到反作用。

图6 不同偏心距的储热量，熔化时间及熔化速率Fig.6 Heat storage capacity,melting time and melting rate for different eccentric distances

3.3 倾斜角度对熔化过程的影响

在相变材料于封闭腔内的传热过程中，自然对流和接触熔化对强化传热起着重要作用。装有相变材料的封闭容器在不同方向重力的作用下，固态低温PCM紧贴加热壁面，熔化的高温液态PCM受到排挤沿着加热面被排出，形成了一层薄的液膜从而获得较高的加热率。图7 展示了每隔120 min，当X=5 的楔形罐倾斜不同角度时固液界面的动态变化，当θ=0°时，换热壁面处于罐体正中心，重力垂直向下。固态PCM 的密度大于已经熔化的高温液态PCM，固态PCM的熔化会沿着重力方向发生沉降，熔化的液体会随着固态相变材料的沉降被挤向两侧，所以可以看到其相界面的位置呈现凹型，中间熔化多，两侧熔化少。当倾斜一定角度时，重力不再只有垂直向下的作用力，在水平方向有了分力，所以当液体被挤向两侧时，由于两侧的受力平衡被打破从而使倾斜侧的熔化加剧，使固液界面呈现C 型分布。倾斜一定角度会增大固态PCM 与罐体上部空气的接触面积，倾斜角度越大，接触面积越大，自然对流越强，蓄热效率越大。当液相分数为1时，认为蓄热罐充电完成。以θ=0°为标准，当θ=45°时蓄热效率开始有大幅度提升，当θ=75°时蓄热效率增长到最大，提升了29%。在传统矩形的基础上，改进结构为楔形比X=5，偏心距为0，倾斜角度为75°放置的楔形管壳式蓄热罐的储热效率比传统矩形提高了39%。

图7 不同倾斜角度熔化进程中固液相界面的变化Fig.7 Changes in the solid-liquid interface during melting with different tilt angles

图8 展示了罐体每倾斜15°的——-Nu数随Fo数的变化情况，平均Nusselt数随Fourier数的变化可以用于确定熔化过程中对流强度大小。不同倾斜角度的——-Nu数具有相同的变化趋势，先急剧增大后再缓慢下降，最终趋于一致。这是由于在熔化初期，倾斜一定角度会加大与罐体上部空气的接触面，加强对流换热强度，所以倾斜0°时对流换热强度最低，倾斜75°时最高。随着高温液态石蜡的增多，其导热热阻越来越大，石蜡与换热壁面的温差越来越小，导致传热急剧恶化，所以——-Nu数急剧下降。放大图8可以看到在熔化后期，倾斜角度为75°时，其对流强度却低于倾斜角度为0°的罐体，这是因为倾斜75°的罐体在同一时刻熔化的液态石蜡远多于倾斜0°的罐体，热阻的阻碍作用高于自然对流的强度。

图8 不同倾斜角度的熔化进程中——-Nu数随Fo数变化情况Fig.8 Variation of number with Fo number for melting processes with different tilt angles

4 结 论

对传统矩形管壳式储热系统进行了增强自然对流技术的改进，数值模拟分析了不同的楔形比、偏心距及倾斜角度时储能系统内的传热动态机制，得到以下结论。

（1）通过削减矩形下部壳体尺寸来改善系统底部蓄热速率过低的手段是有效的，但是当下部壳体尺寸削减过多时，罐体整体高度增加，高温液态PCM 难以在重力的作用下向下流动传热。当X=5时，蓄热系统内PCM的完全熔化时间最短，熔化时间缩短比率最高，为28%。

（2）相变材料的熔化速率会随着内流管偏心距的增大而降低，表明偏心距对竖直放置蓄热系统内相变材料的熔化效率会起到反作用。

（3）罐体倾斜一定角度会增大自然对流的强度，换热过程中数随着Fo数的增大而增大，然后再急剧减小。当倾斜75°时，自然对流增强的效果最显著。

（4）在传统矩形的基础上，改进结构为楔形比X=5，偏心距为0，倾斜角度为75°放置的楔形管壳式蓄热罐的储热效率比传统矩形提高了39%。

符号说明

Amush—— 糊状区常数，kg/(m3·s)

cp—— 比热容，J/(kg·K)

g—— 重力加速度，m/s2

H—— 总焓，J/kg

HPCM—— 相变单元高度，m

h—— 焓值，J/kg

h0—— 参考温度300 K下PCM的焓值，J/kg

k—— 导热系数，W/(m·K)

L—— 相变潜热，kJ/kg

m—— 质量，kg

Q—— 储能量，J

S—— 源项

T—— 温度，K

T0—— 参考温度300 K下PCM的温度，K

Tave—— 平均温度，K

Tini—— 初始温度，K

Ts—— 固相线温度，K

TL—— 液相线温度，K

tw—— 壁面温度，K

tr—— 熔点温度，K

t—— 时间，s

v—— 速度，m/s

W—— 相变单元宽度，m

ƒ—— 液相分数

ρ—— 密度，kg/m3

ρ0—— 参考温度300 K下PCM的密度，kg/m3

μ—— 动态黏度，kg/(m·s)

ɑ—— 热扩散率，m2/s

ε—— 数值常数

β—— 体积膨胀系数，K-1

φ—— 储能速率，J/s