基于冗余阵元优化的双基地嵌套MIMO雷达目标DOD和DOA联合估计方法

游致远, 胡国平, 周 豪

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

多输入多输出(multiple input multiple output, MIMO)雷达理论被人提出后[1],因其可以发射特殊的波形信号以及更高的自由度[2-4],受到国内外广大学者的关注和研究。因为MIMO雷达经过“和联合”阵列形成的阵列与普通阵列在信号处理方面大致相同,所以在MIMO雷达进行波达方向角(direction of arrival, DOA)估计时,也可以使用很多经典空间谱估计算法。直到现在,大量的空间谱估计算法[5-9]被学者们提出并开展深入研究,这些算法也被学者用来解决二维空间谱峰搜索和角度匹配所形成的算法高复杂度问题,并且解决角度估计精度不理想的问题。为了解决传统均匀线阵阵列孔径过小、信源个数不能多于天线阵元个数和自由度性能差等问题,又有学者提出将稀疏阵列引入目标参数联合估计中,常见的稀疏阵列主要包含互质阵列[10]、嵌套阵列[11]、最小冗余阵列[12]等。

文献[13]通过二维扩展对基于旋转不变技术的信号参数估计(estimating signal parameter via rotational invariance techniques, ESPRIT)算法进行改进,很好地将其应用到双基地MIMO雷达对目标的收发角估计上,但该算法存在要对收发角进行手动角度配对的问题,算法的复杂度较大。一种适用于双基地嵌套MIMO雷达的算法在文献[14]中提出,此算法可以利用目标距离信息解决角度歧义的问题,从而实现目标收发角的自动匹配,同时保证对目标收发角的高精度估计,但该算法在自由度性能方面效果不理想,无法对多个目标进行有效估计。文献[15]研究了双基地嵌套MIMO雷达目标估计中的自由度扩展问题,提出了尽可能多地构造连续的“差联合”结构形式的虚拟阵元,能充分地通过稀疏阵列孔径扩展来实现目标收发角联合估计在自由度方面的提升,但是存在估计精度和分辨性能不理想的问题。在文献[16]中,提出了一种结合张量分解和双基地嵌套MIMO雷达估计的算法,该算法通过二维空间平滑算法重构了新的协方差矩阵,并从波离方向角(direction of departute,DOD)和DOA维度推广了三阶张量模型,并利用现有的复平行因子(complex parallelism factor, COMFAC)技术进行角度估计,但该算法与文献[14]所提出的方法相比,在估计精度上仍有不足。本文改进了二维空间平滑算法,通过重建Toeplitz矩阵以及虚拟发射阵列和虚拟接收阵列的空间平滑矩阵的方法,来解决因向量化协方差矩阵导致的单快拍问题和自由度性能不足的问题,并能对多目标收发角进行自动配对,并与文献[17]提出的传统双基地均匀线阵MIMO雷达进行了对比。为了能减小信息损失、提高角度估计精度,本文还针对在传统算法中没有充分利用的“差联合阵列”位置上的冗余阵元,通过充分利用每个位置上的冗余阵元,不断优化接收信号中的目标参量信息,并与文献[18]提出的算法进行比较,仿真实验验证了该算法在DOD和DOA的估计分辨性能和估计精度方面比双基地[19-24]嵌套MIMO雷达常规算法效果更理想。

1 双基地嵌套MIMO雷达模型

双基地嵌套MIMO雷达模型如图1所示,发射阵列由两个发射子阵组成,分别有M1和M2个阵元。同理,接收阵列由两个接收子阵组成,分别有N1和N2个阵元,阵元间距d=λ/2,λ为信号波长。阵列位置可表示为

图1 双基地嵌套MIMO雷达结构图

St={0,…,(M1-1)d,[(M1+1)-1]d,…,

[M2(M1+1)-1]d}

(1)

Sr={0,…,(N1-1)d,[(N1+1)-1]d,…,[N2(N1+1)-1]d}

(2)

若空域内有K个不相干目标,其中第k个目标的DOD和DOA由φk、θk来表示,k=1,2,…,K。其中,第k个信源的发射角由φk来表示,接收角由θk来表示。信号模型为

x(t)=[at(φ1)⊗ar(θ1),at(φ2)⊗ar(θ2),…,at(φK)⊗ar(θK)]s(t)+n(t)=(At∘Ar)s(t)+n(t)=As(t)+n(t)

(3)

式中:s(t)=[s1(t),s2(t), …,sK(t)]T,sK(t)代表第K个目标的发射系数;n(t)表示均值为0、方差为σ2的高斯白噪声组成的矩阵; ∘和⊗分别表示Khatri-Rao积和Kronecker积。导向向量A可表示为

At=[at(φ1),at(φ2),…,at(φK)]

(4)

Ar=[ar(θ1),ar(θ2),…,ar(θK)]

(5)

式中:at(φk)和ar(θk)分别代表发射阵列和接收阵列的第k个目标的导向向量,其结构可表示为

at(φk)=[1,e-jπ sin φk,…,e-j(M2(M1+1)-1)π sin φk]T

(6)

ar(θk)=[1,e-jπ sin θk,…,e-j(N2(N1+1)-1)π sin θk]T

(7)

由式(3)可得到接收信号的协方差矩阵为

(8)

(9)

(10)

2 基于冗余虚拟阵元优化的二维空间平滑算法

2.1 冗余虚拟阵元优化利用

通常在进行协方差矩阵向量化时,传统算法都是将冗余的虚拟阵元删除后重新排序,这种做法没有利用冗余虚拟阵元所带有的目标参量信息,角度估计的性能不理想。所以本文提出了一种基于冗余虚拟阵元再利用的二维空间平滑算法,该算法充分利用了虚拟接收信号冗余的虚拟阵元,使得算法分辨性能上优于常规算法。

(11)

ac(φK,θK)=[at(φK)⊗ar(θK)]*⊗[at(φK)⊗ar(θK)]

(12)

所以根据新形成的虚拟阵列,可以得到和差阵列为

(13)

(14)

(15)

(16)

式中:x表示虚拟阵列中同一位置上冗余阵元个数;Rp(i)表示在虚拟阵列p位置上的第i个协方差数值;Rp′表示在重新赋值后虚拟阵列p位置上的协方差数值。

现将新的协方差矩阵向量化,可以获得一个新的等效虚拟信号,即

(17)

上述操作虽然会增加算法的时间复杂度,但是增加的运算量全部来自于未利用到的协方差矩阵数据,将协方差矩阵中的冗余虚拟阵元信息利用后,目标的DOD和DOA联合估计性能将得到提高。

2.2 重建Toeplitz矩阵的二维空间平滑算法

通常对传统均匀线阵双基地MIMO雷达进行角度联合估计使用二维多重信号分类(multiple signal classification, MUSIC)算法或ESPRIT算法,但是向量化样本协方差矩阵引起的单快拍问题依旧没有解决,而且针对多目标联合估计,通常都会存在阵列自由度问题。为此,先定义两个选择矩阵,一个选择矩阵选择平滑虚拟发射阵列,另一个选择矩阵选择平滑虚拟接收阵列,在虚拟发射阵列和虚拟接收阵列中构建空间平滑子阵并且重新构建Toeplitz矩阵,根据新的Toeplitz矩阵再次构建全新的协方差矩阵,最后利用常规子空间类算法对虚拟接收信号进行空间谱估计得到目标的发射角和接收角。

通过将冗余阵元再利用后,得到具有连续虚拟阵元的等效虚拟信号向量,即

(18)

(19)

(20)

式中:M0=M2(M1+1),N0=N2(N1+1)。

(21)

(22)

(23)

重新构建的Toeplitz矩阵为

(24)

根据式(23),每个子阵的协方差矩阵为

(25)

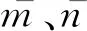
(26)

(27)

(28)

式中:En代表协方差矩阵的信号子空间。

(29)

因此,式(28)可以表示为

(30)

再定义式(30)中的一个分式为

(31)

所以,式(28)还可以表示为

(32)

则第k个目标的DOA可表示为

(33)

式中:e1=[1,0,…,0]T。

具体步骤如算法1所示。

算法 1 重建Toeplitz矩阵的二维空间平滑算法输入 x(t)=As(t)+ν(t),t=1,2,…,L;输出 {φ^k,θ^k},k=1,2,…,K;步骤 1 推导经过匹配滤波后的虚拟接收信号R,并对其近似表示为R^;步骤 2 将冗余虚拟阵元充分利用,得到新的协方差矩阵R^-,对其向量化得到观测向量r-;步骤 3 对观测向量r-引入两个选择矩阵分别对应虚拟发射阵列和虚拟接收阵列,通过选择矩阵,重新构建Toeplitz矩阵Rc;步骤 4 利用Toeplitz矩阵重构的二维空间平滑方法,得到了虚拟阵列的协方差矩阵R-c;步骤 5 通过降维MUSIC算法实现DOD和DOA自动匹配,并得到{θ^k,φ^k}。

3 仿真实验和结果分析

3.1 场景设定

假设本文中的的发射子天线阵元数为M1=2,M2=3;接收子天线阵元数为N1=2,N2=3,即M=N=5。设定本次实验次数为200次,均方根误差(root mean squared error, RMSE)的计算表达式为

(34)

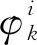
3.2 目标DOD和DOA估计的自由度性能和分辨性能

本文通过对比基于本文改进算法的双基地嵌套MIMO雷达与文献[17]的传统双基地均匀线阵MIMO雷达的归一化空间谱等高线图,验证了本文提出的重建Toeplitz矩阵的二维空间平滑算法得到的自由度M0N0大于传统双基地均匀线阵MIMO雷达的自由度MN,同时能保证其能对多个目标进行角度估计;然后通过对比文献[18]提出的双基地嵌套MIMO雷达的常规算法与本文提出改进算法的归一化空间谱峰图,可以说明本文提出的利用冗余虚拟阵元算法在分辨性能上比常规算法效果更优。

若实验的信噪比(signal to noise ratio,SNR)大小为10 dB,快拍次数为500,目标的收发角在0°至30°范围内分布,DOD估计值为1°∶2°∶3°∶9°∶12°∶14°∶25°∶26°∶28°,DOA估计值为5°∶15°∶28°∶2°∶13°∶24°∶4°∶14°∶27°,估计目标数目为9。图2(a)给出了传统双基地均匀线阵MIMO雷达的空间谱等高线图,图2(b)给出了基于改进算法的双基地嵌套MIMO雷达的空间谱等高线图。从图2可以看出,传统MIMO雷达在估计目标数目为6,谱峰数小于目标数,目标分辨性能弱,不能较好地测得目标数量和目标方向。而改进算法的嵌套MIMO雷达可以准确分辨9个目标的方位,并且等高线无重叠现象出现,在相同物理阵元的情况下,基于本文改进算法的双基地嵌套阵MIMO雷达在自由度方面优于传统均匀线阵双基地MIMO雷达。

图2 两种MIMO雷达空间谱等高线图

在同样假设的情况下,对文献[14]提出的基于常规算法的双基地嵌套MIMO雷达和基于本文改进算法的双基地嵌套MIMO雷达的空间谱峰图进行对比分析。图3(a)表示基于常规算法的双基地嵌套MIMO雷达的空间谱峰图,图3(b)表示基于改进算法的双基地嵌套MIMO雷达的空间谱峰图。从图3可以看出,改进算法相较于常规算法充分利用了虚拟冗余阵元,极大减小了虚拟阵列信号的信息损失,明显提升了对目标角度估计的分辨性能。

图3 基于两种算法嵌套MIMO雷达空间谱峰图

3.3 目标DOD和DOA估计的RMSE

假设空间中目标数目为3个,其角度信息为(φ1,θ1)=(11°,19°),(φ2,θ2)=(15°,17°),(φ3,θ3)=(22°,27°),对目标方位角度的搜索步长为0.1°。图4(a)表示传统双基地均匀线阵MIMO雷达、基于常规算法的双基地嵌套MIMO雷达和基于改进算法的双基地嵌套MIMO雷达的角度RMSE随SNR变化图, SNR的变化范围为-10 dB至10 dB,其间隔为2 dB。为凸显变化程度，纵轴采用对数坐标。图4(b)表示传统双基地均匀线阵MIMO雷达、基于常规算法的双基地嵌套MIMO雷达和基于改进算法的双基地嵌套MIMO雷达的角度RMSE随快拍数变化图,SNR设置为10 dB,快拍数设置为从100次到500次,间隔50次。从图4可知,在相同物理阵元的情况下,嵌套阵结构MIMO雷达在估计精度方面优于传统均匀线阵结构的MIMO雷达。在算法不同的情况下,由于本文的改进算法利用了冗余的虚拟阵元,目标角度信息都已充分利用,因此算法性能优于常规算法。

图4 RMSE随SNR和快拍数的变化关系

3.4 目标DOD和DOA估计的算法复杂度

根据前文可知,本文提出的基于冗余阵元优化利用的二维空间平滑算法在自由度性能和估计精度方面分别优于文献[17]的双基地均匀线阵MIMO雷达传统算法和文献[14]提出的双基地嵌套阵MIMO雷达常规算法,但本文提出的算法仍有不足。图5表示几种算法的时间复杂度对比图,在算法复杂度方面,本文提出的算法复杂度略高。

图5 算法复杂度对比图

4 结束语

本文提出了一种基于冗余虚拟阵元再利用的二维空间平滑算法,该算法充分地利用冗余虚拟阵元,有效地减小了虚拟阵列信号的信息损失,明显提升了对目标角度估计的分辨性能。针对多目标问题,本文选择了一种重建Toeplitz矩阵的空间平滑算法,不仅很好地扩展了虚拟阵列提升了自由度,并且利用降维MUSIC算法解决了DOD和DOA自动配对的问题。然而,本文提出的算法也仍存在不足,虽然算法估计精度较高,但是其时间复杂度也高。而且,此算法虽然有较高的自由度,但是自由度性能并不能到达理论推导的效果,在目标数目估计上仍存在一定自由度损失的情况，这将成为下一步研究的重点。