永磁同步电机双矢量无权重模型预测转矩控制

陈商玥，高 强，陈 愚

(1.天津理工大学 电气电子工程学院，天津 300380；2.国网天津市电力公司 城西供电分公司，天津 300110；3.天津中德应用技术大学 智能制造学院，天津 300350)

0 引 言

永磁同步电机(以下简称PMSM)驱动器高性能控制的主要控制策略为磁场定向控制和直接转矩控制[1]。模型预测控制(以下简称MPC)以其动态响应快、可直接控制多个目标等优点，被应用于电机控制领域[2]。

MPC可分为模型预测电流控制和模型预测转矩控制[3]。与模型预测电流控制相比，模型预测转矩控制目标函数包含转矩分量和磁链分量，能够直接控制转矩控制。由于转矩与磁链量纲不同，需在目标函数加入权重系数以平衡转矩和磁链的影响程度。然而权重系数需要不断调整，繁琐且耗时[4]。

为了消除权重系数，文献[3]通过转矩和磁链无差拍求出最优电压矢量，构建基本电压矢量和最优电压矢量之差的目标函数，消除了量纲。文献[5]的目标函数为定子磁链矢量误差，无需权重设计。文献[6]计算不同基本电压矢量作用下的转矩和磁链误差，分别对转矩和磁链误差排序，选择排序后序号之和最小值对应的基本矢量作为最优矢量。文献[7]提出一种级联MPC方法，根据控制变量的优先级，先选择使优先级最高的控制变量预测误差最小的基本矢量组合，再从中选择使优先级次之的控制变量预测误差最小的矢量作为最佳矢量，但该方法未说明矢量集合的一般选取方法。文献[8]在文献[7]的基础上比较了先对磁链误差排序再对转矩误差排序和先对转矩误差排序再对磁链误差排序的优劣。文献[7-8]没有给出当同时存在两个最小值时最优矢量的选取方法。文献[9]分别选择使得转矩和磁链误差最小的三个基本矢量，再从两组基本矢量中选择共有的基本矢量作为最佳矢量。此外，还可以通过构建控制变量的镜像表达式[10]、归一化[11]等方法消除权重系数。

传统的模型预测转矩控制一个控制周期只作用一个基本矢量，转矩和磁链脉动较大。为提高稳态性能，占空比控制被应用于模型预测转矩控制，传统方法首先通过目标函数选出最优矢量，然后再计算占空比[12]，所选电压矢量的目标函数值不一定最小，且目标函数仍包含权重。文献[13-14]分别通过目标函数最小化、转矩误差积分最小化求解矢量作用时间。文献[15]将两个备选矢量两两组合，提高了稳态性能，但是计算量较大。文献[16]将查表法得到的备选矢量和所有基本矢量两两组合，和文献[15]相比计算量虽有所减小，但矢量覆盖的区域有重复，计算量仍然较大。文献[17]通过转矩和磁链误差的大小确定备选矢量，目标函数为转矩无差拍矢量作用时间和磁链无差拍矢量作用时间之和。文献[18]选取第一个矢量的方法和文献[16]相同，第二个矢量从第一个矢量相邻的矢量及零矢量中选择。文献[19]通过磁链矢量的增量所在扇区来确定备选矢量组合，减小了计算量；占空比通过转矩和磁链幅值无差拍确定。此外，增加备选矢量亦可提高稳态性能[20]。

为了消除权重系数，本文将转矩误差和磁链误差转换到α，β坐标系下，构建以矢量到转矩误差直线和磁链误差圆的距离之和的目标函数。仿真和实验验证了本方法的有效性和可行性。

1 数学模型

两电平电压源逆变器驱动PMSM系统拓扑如图1所示。图1中，udc表示直流电压，Cdc表示直流侧纹波吸收电容，S1～S6构成了三相电压型逆变桥，ia、ib、ic表示三相PMSM定子电流。

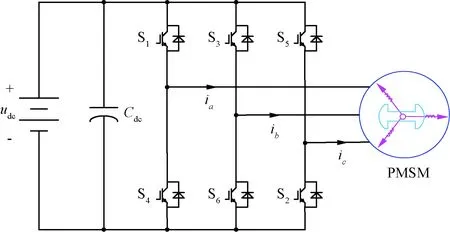
图1 三相电压源型逆变器PMSM驱动系统拓扑结构

两电平电压源逆变器共有8种开关状态，对应8种基本电压矢量，其空间分布如图2所示。

图2 矢量空间分布图

两相旋转坐标系下，PMSM电压方程可表示：

(1)

(2)

式中：Rs,ωe分别表示定子电阻和电角频率；ud，uq表示d，q坐标系下定子电压；id，iq表示d，q坐标系下定子电流；ψd，ψq为d，q坐标系下定子绕组磁链，其表达式：

ψd=Ldid+ψf

(3)

ψq=Lqiq

(4)

式中：Ld，Lq为d，q坐标系下的等效电感;ψf为永磁体磁链。

d，q坐标系下的转矩和磁链方程：

(5)

(6)

式中：p为极对数。

采用一阶欧拉公式得到id、iq预测公式：

(7)

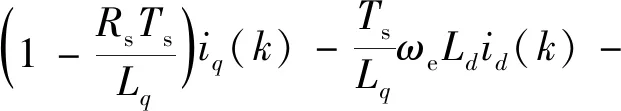
(8)

(9)

(10)

式中：id(k)、iq(k)，ud(k)、uq(k)分别为kTs时刻d，q坐标系下定子电流、定子电压；id(k+1)，iq(k+1)分别为(k+1)Ts时刻d，q坐标系下定子电流预测值；Te(k+1)，ψs(k+1)分别为(k+1)Ts时刻转矩和磁链预测值；Ts为采样周期。

2 传统预测转矩控制

传统单矢量模型预测转矩控制代价函数如下：

g=|Teref-Te(k+1)|+λ|ψsref-ψs(k+1)|

(11)

式中：Teref与ψsref分别表示转矩与磁链的给定值。ψsref表达式:

(12)

将8个基本电压矢量代入式(7)～式(11)，选择使g最小的基本电压矢量，输出给逆变器。

对转矩和磁链单独定义代价函数，表示如下:

gTe=|Teref-Te(k+1)|

(13)

gψ=|ψsref-ψs(k+1)|

(14)

传统占空比预测转矩控制(以下简称Duty-PTC)先通过目标函数选择最佳有效矢量uopt，再通过转矩无差拍的原则计算uopt的占空比，不能保证uopt全局最优。如图3所示，通过目标函数选择的最佳矢量为u2，由于u0作用效果的方向为斜向下，但其作用时间为零，则u2和u0合成矢量为u2，此时误差仍然存在。

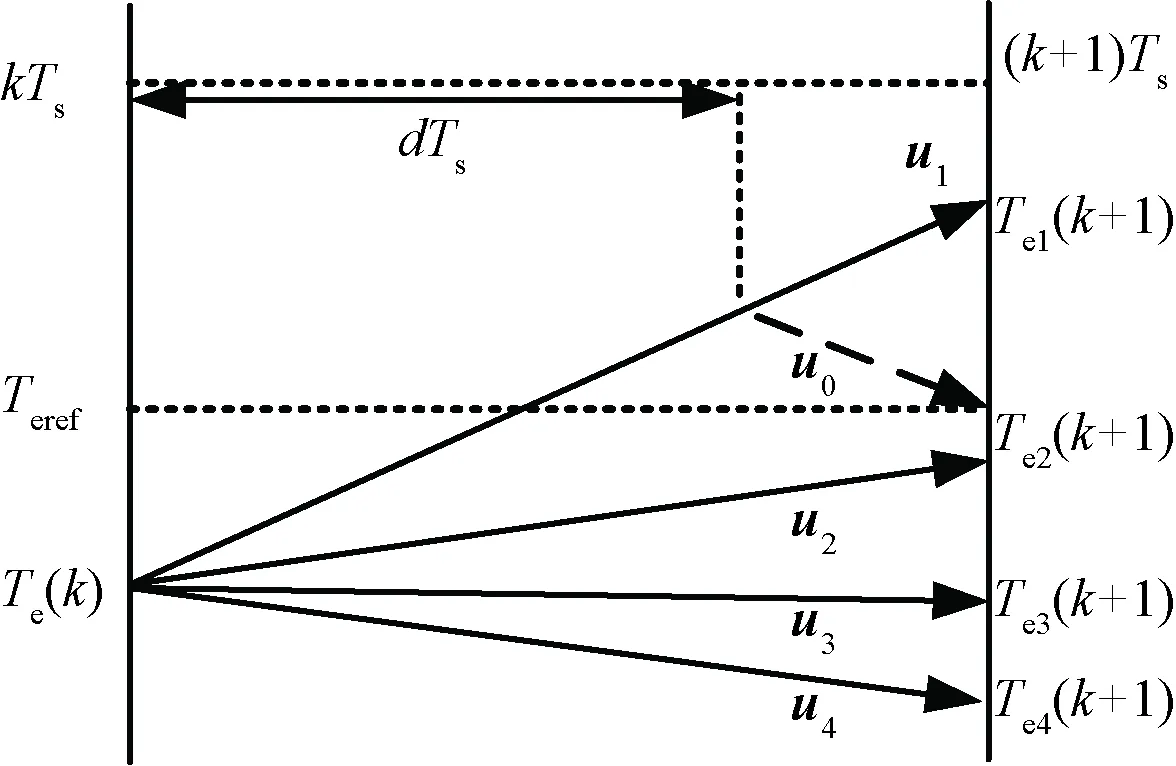
图3 矢量选择示意图

由式(9)可知，零矢量作用时Te变化率sT0:

(15)

(16)

有效电压矢量作用时Te变化率sTi：

(17)

式中:udi(k)和uqi(k)分别为第i个有效矢量ui的d,q轴分量，i=1,2,…,6。

加入占空比后的转矩预测值:

Te(k+1)=Te(k)+sTidiTs+sT0(1-di)Ts

(18)

令Te(k+1)=Teref，可得ui的占空比：

(19)

将di代入式(11)，选择gi最小的di。

3 双矢量无权重预测转矩控制

由Teref=Te(k+1)及式(5)可得:

(20)

结合式(7)和式(8)，设:

id(k+1)=k1+kud

(21)

iq(k+1)=k2+kuq

(22)

式中:

(23)

(24)

(25)

则将式(21)～式(24)代入到式(19)并转换到α,β坐标系，有:

(26)

记:

(27)

由式(25)知，Teref=Te(k+1)在α,β坐标系下对应一条直线l，可以将式(13)转换为任意矢量(uα,uβ)到l的距离dT，dT表达式:

dT=|-uαsinθ+uβcosθ-dT|

(28)

将式(20)～式(24)代入到ψsref=ψs(k+1)并转换到α,β坐标系，有:

(29)

式中：

(30)

(31)

ψsref=ψs(k+1)在α,β坐标系下对应一个圆c，圆上任意点均满足磁链无差拍，可以将式(14)转换为任意矢量(uα,uβ)到c的距离dF，dF表达式:

(32)

由式(28)和式(32)可知，dT和dF均为同一坐标系下的距离公式，有相同的含义，故可以构建新的无权重目标函数如下:

g=dT+dF

(33)

记所本提方法为SVB-NWF-PTC，其选择矢量的示意图如图4所示。

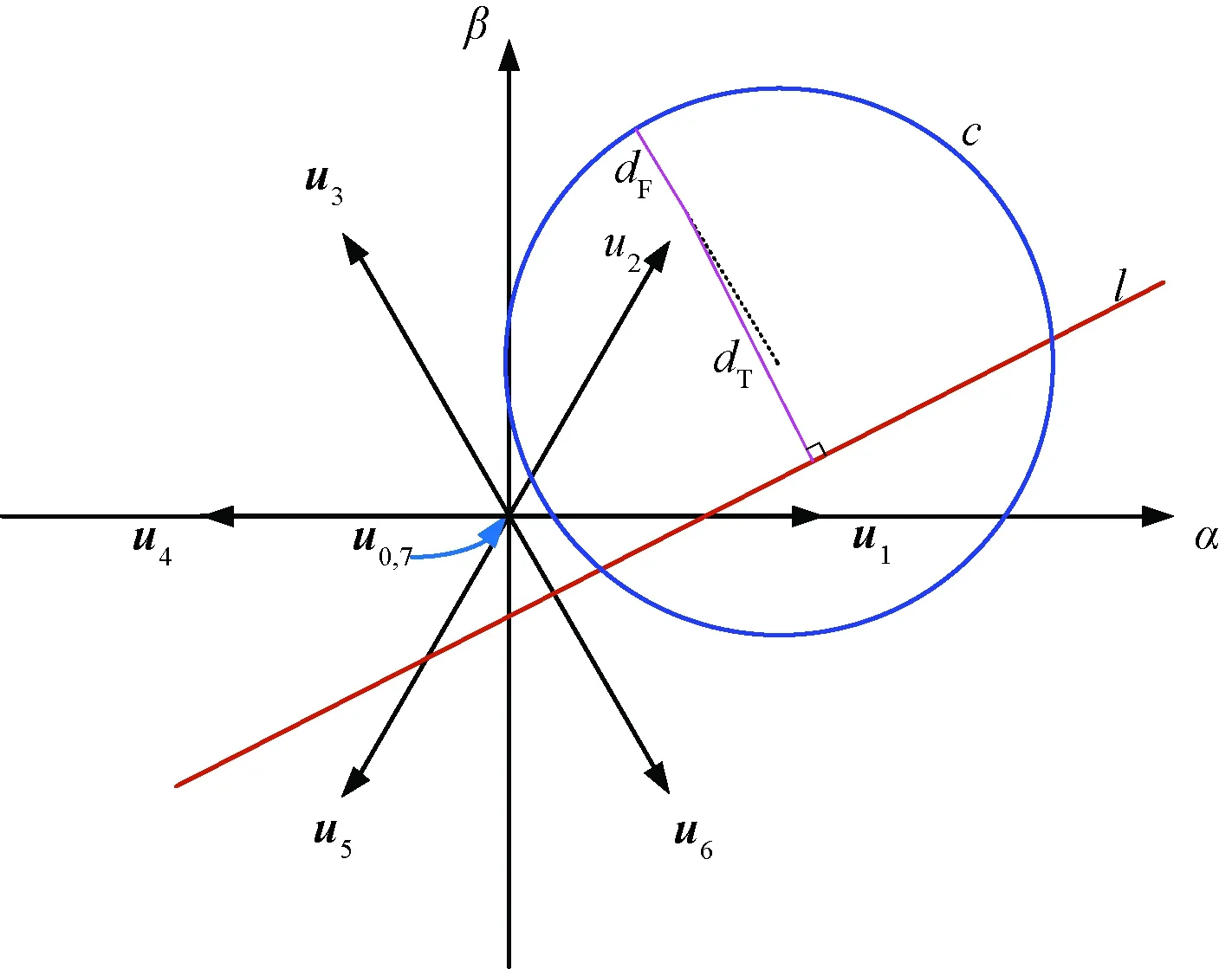
图4 SVB-NWF-PTC矢量选择示意图

基于式(33)引入占空比，记为SVB-NWF-PTC，可以借助式(13)或式(28)分别求解作用时间。

(1) 基于式(13)

该方法和Duty-PTC采用的方法完全相同。求出ui占空比di后，ui和u0合成矢量为(diuαi，diuβi)，将其代入式(33)，寻优后得到uopt和dopt。

(2) 基于式(28)

对于矢量ui和u0，有：

dTi+dT0=di(-uαisinθ+uβicosθ)

(34)

(35)

令dT=0，di表达式如式(35)所示。若di>1，则di=1；若di<0，则di=0。然后将ui和u0合成的矢量(diuαi，diuβi)代入式(33)寻优。SVB-NWF-PTC控制框图如图5所示。

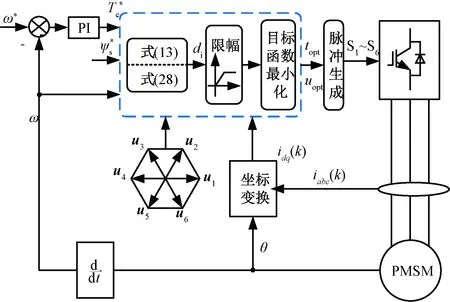
图5 SVB-NWF-PTC控制框图

4 仿真与实验分析

为了验证SVB-NWF-PTC的有效性，给出了Duty-PTC和本方法的加减转速、加减负载和稳态仿真波形。PMSM参数如表1所示，采样频率设置为20 Hz。

表1 PMSM参数

在转速1 000 r/min、转矩8 N·m和额定转速3 000 r/min额定负载15 N·m两种工况下，PMSM都设置空载起动，在0.2 s时突加负载转矩，比较Duty-PTC和SVB-NWF-PTC的A相定子电流ia和THD分析，如图6和图7所示。

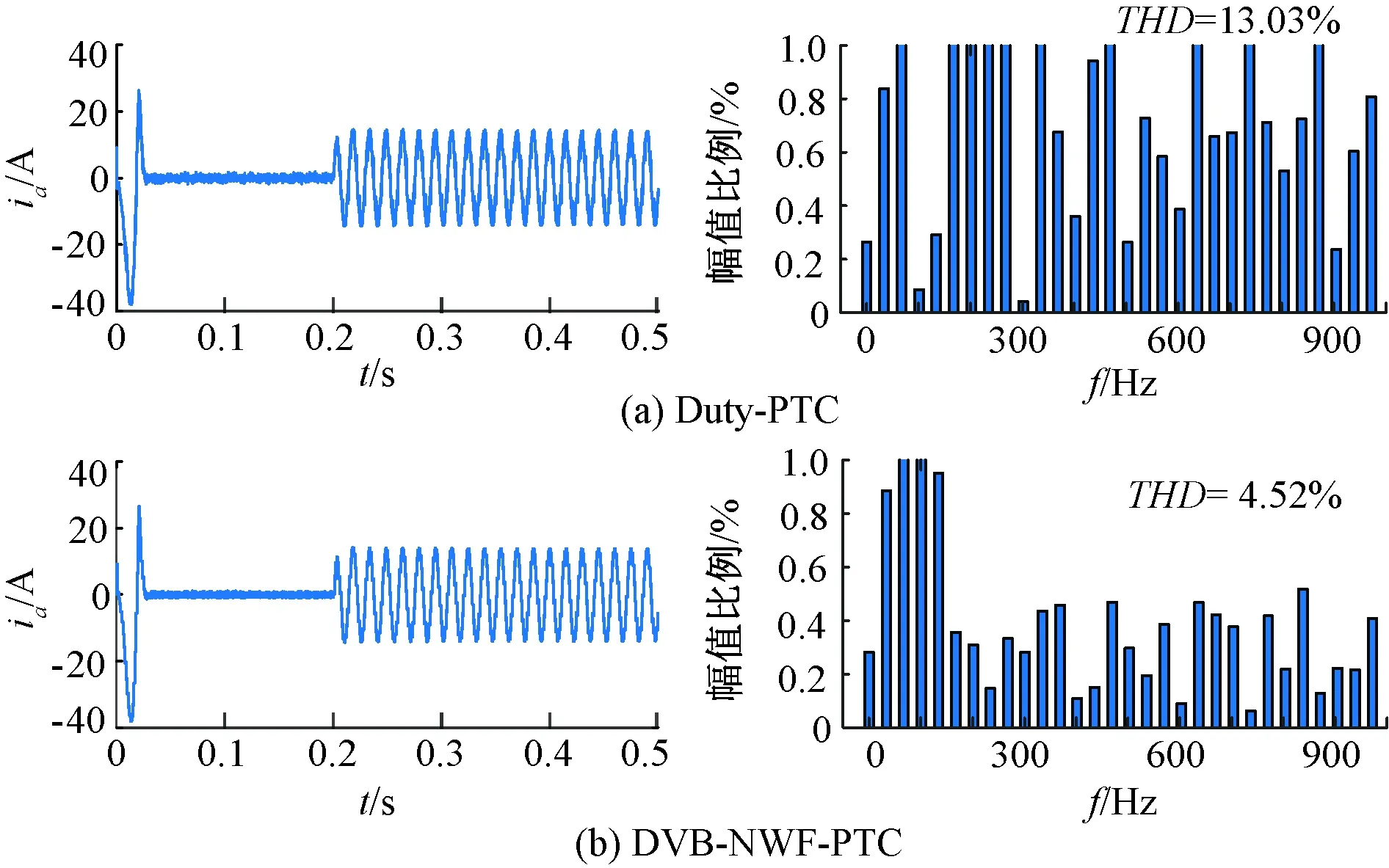
图6 转速1 000 r/min、转矩8 N·m下的相电流及THD分析

图7 额定转速、额定转矩15 N·m下相电流及THD分析

由图6和图7可得，相较于Duty-PTC，转速1 000 r/min和转矩8 N·m下本方法A相电流谐波畸变率THD减小了65.31%；额定转速、额定转矩条件下本方法A相电流谐波畸变率THD减小了20.40%。

两种工况下本方法和Duty-PTC的转矩和磁链脉动如图8、图9所示。

转矩和磁链脉动表达式如下：

(36)

(37)

式中:Te_ripple和ψe_ripple分别为转矩和磁链脉动；N为采样个数；Te_ref和ψe_ref分别为转矩和磁链参考值。

由图8和图9可知，不同工况下，本方法的转矩和磁链脉动都小于Duty-PTC。

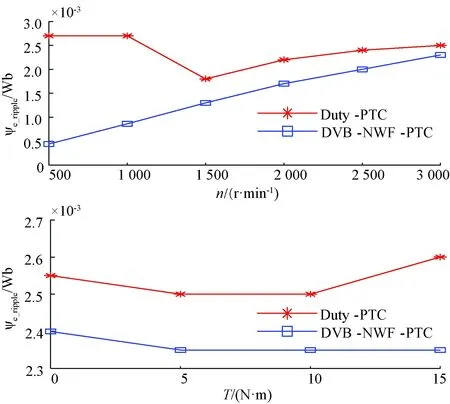
图8 转矩8 N·m、不同转速和额定转速、不同转矩条件下Duty-PTC和SVB-NWF-PTC的磁链脉动

图9 转矩8 N·m、不同转速和额定转速、不同转矩条件下Duty-PTC和SVB-NWF-PTC的转矩脉动

PMSM加减负载设置：0.2 s时突加10 N·m负载，0.3 s时突加15 N·m负载；0.4 s时将负载突减至5 N·m。图10和图11分别为Duty-PTC和SVB-NWF-PTC加减负载仿真波形。PMSM空载起动，两种方法的转矩达到限幅值，Duty-PTC的转矩脉动大于SVB-NWF-PTC。突加或突减负载，两种方法均经过约50 ms加速到给定转速2 000 r/min，动态性能基本相同。

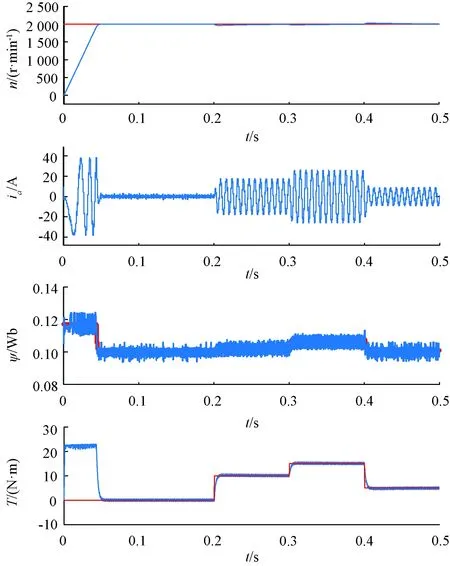
图10 Duty-PTC加减负载仿真波形

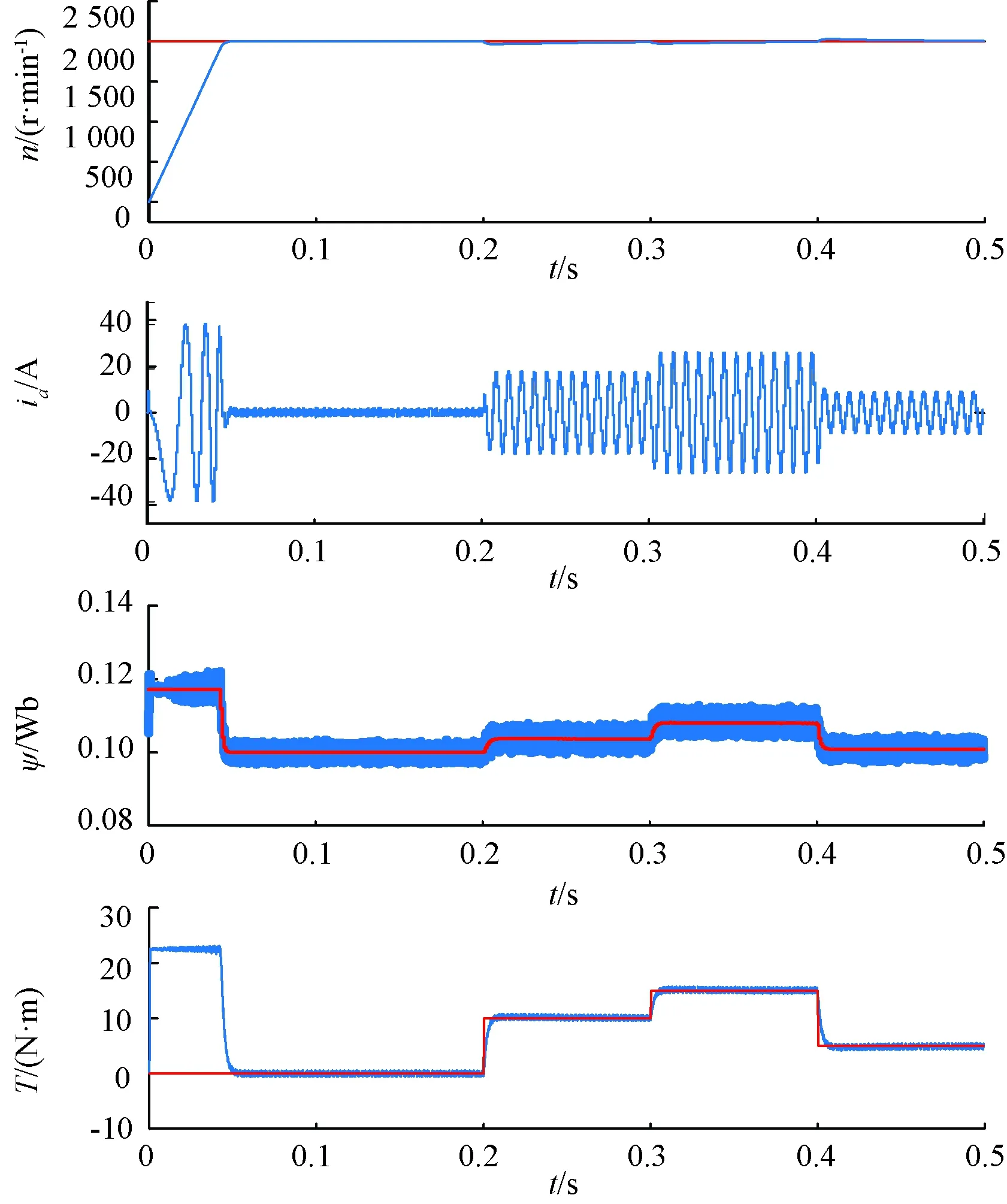
图11 SVB-NWF-PTC加减负载仿真波形

图12给出了转速800 r/min，负载转矩8 N·m工况下Duty-PTC与SVB-NWF-PTC两种控制策略的稳态实验波形。Duty-PTC下，电流谐波畸变率THD为13.62%，而SVB-NWF-PTC能显著改善稳态性能，电流谐波畸变率THD仅为5.98%，其转矩与磁链脉动也均小于Duty-PTC。

图12 转速800 r/min、转矩8 N·m条件下相电流及THD分析

5 结 语

为了消除权重系数并提高稳态性能，本文提出了一种双矢量无权重预测转矩控制方法。仿真结果表明，与Duty-PTC相比，本方法无需权重系数，能进一步减小相电流谐波畸变率THD、转矩脉动和磁链脉动，动态性能和Duty-PTC基本相同。