基于递归神经网络的超声波电机力矩迟滞辨识

傅 平

(1.闽江学院 物理学与电子信息工程学院，福州 350121；2.闽江学院 福建省教育厅先进运动控制重点实验室，福州 350121)

0 引 言

超声波电机[1-3]是利用压电材料具有的逆压电效应，并利用谐振将电能转变成机械振动能，再通过摩擦转变成旋转或其它方式运动的驱动装置。与传统的电磁型电机相比，它没有绕组和磁性材料，具有结构简单、质量轻、低速大力矩、响应速度快(几毫秒以内)、控制精度高和电磁兼容性好等优点。在非连续运动领域及精密控制领域，超声波电机要比电磁型电机优越得多。

想要充分发挥超声波电机精度高和直接驱动的特点，就必须对其进行精确控制。超声波电机是一个机电耦合的非线性系统，影响电机力矩输出的变量较多，如电机输入电压、相位差、频率、负载等，而这些变量与输出之间是强非线性关系，给精确控制造成了一定困难。对于超声波电机的时变、强非线性特性，其数学解析模型难以得到解析解且建模难度较大。虽然现在已有一些不使用数学解析模型的控制方法，如负载自适应[4]、模糊控制[5]、模型参考自适应[6]、滑模控制[7]、模糊神经网络[8-9]等，但是这些控制方法运算量较大，实时控制时需要处理大量数据，使得控制系统变得复杂。此外，超声波电机的定子使用压电材料，定子压电迟滞通过定转子之间的摩擦层耦合到转子，这也使得电机的速度和输出力矩存在迟滞[10]。近年来，压电作动器(包括超声波电机)的迟滞非线性建模及控制器设计[11-14]是一个热门领域。现有针对压电驱动平台有许多迟滞非线性建模的方法，但是超声波电机输出力矩迟滞的建模涉及较少，主要是由于压电平台的输出量可以通过传感器进行测量，超声波电机可以直接测量的机械量为速度、力矩等，而定子迟滞不易测量。为了发挥超声波电机高精度特点，必须对速度进行精确控制。当电机进行速度跟踪时，其速度-力矩之间的迟滞关系是本文研究的重点。

本文提出使用递归神经网络辨识器(以下简称RNNI)，利用李雅普诺夫稳定性方法进行RNNI的参数调整，对超声波电机速度-力矩迟滞特性进行辨识，其辨识算法可以反映电机的速度-力矩迟滞非线性特性。首先介绍超声波电机的迟滞特性及相关的测控系统，然后给出RNNI的辨识算法，最后根据本文辨识算法得到相关的实验结果并验证该算法的有效性。

1 超声波电机的迟滞特性

超声波电机驱动电路采用基于LCC谐振的电路[15]，如图1所示，整个电路由半桥电路和二相LCC驱动电路组成。外部控制器与相应的驱动电路产生开关元件SW1～SW4以及SW11、SW12所需的驱动信号。

图1 二相半桥式LCC驱动电路

本文所用的超声波电机工作频率为41.5～44 kHz。通过调整二相LCC驱动电路的驱动频率、相位差以及电压幅度可以调节电机的速度，其中测控系统使用灵奇创思控制卡完成电机速度和力矩数据的采集。电机测试系统的框图如图2所示。

图2 电机测试系统框图

超声波电机的控制变量主要有电压、驱动频率和相位差。由文献[4-9,11-14] 可以知道，电机的频率-速度特性与相位差-速度特性均为非线性，但是对力矩-速度的迟滞特性未进行描述。利用基于半实物仿真的电机测试系统，当电机跟踪给定速度y=70+20sin(2πft) (f=1.2 Hz)，负载为0.126 N·m，并使用PI控制器调节频率和相位差控制速度，得到电机速度随时间变化的特性如图3(a)所示，对应的频率-速度特性如图3(b)所示，速度-力矩特性如图3(c)所示。由图3可知，电机的速度-力矩特性存在迟滞，频率-速度特性也存在迟滞，且图3(c)的光滑性较图3(b)差。

图3 速度y=70+20sin(2πft)时的特性曲线

为了验证不同速度和不同给定曲线下也存在频率-速度和速度-力矩迟滞，我们改变跟踪速度范围和跟踪曲线类型进行上述类似实验。当电机跟踪给定三角波速度，其速度区间设为50～90 r/min，三角波的频率为1.1 Hz，负载为0.126 N·m，使用PI控制器控制速度，得到电机速度随时间变化的特性如图4(a)所示，其对应的频率-速度特性如图4(b)所示，速度-力矩特性如图4(c)所示。由图4可知，电机的速度-力矩迟滞特性较为明显，频率-速度虽然也呈现迟滞特性，但是迟滞特性边缘波动较大且光滑性较差。

图4 速度三角波50～90 r/min时的特性曲线

改变跟踪三角波速度的范围，设为30～80 r/min，三角波的频率为1.2 Hz，负载为0.126 N·m，与前面实验方法类同，得到电机速度随时间变化的特性如图5(a)所示，其对应的频率-速度特性如图5(b)所示，速度-力矩特性如图5(c)所示。虽然跟踪给定的速度区间不同，但图5(c)的速度-力矩也存在迟滞。频率-速度也呈现迟滞，由图4(b)与图5(b)对比可知，迟滞边缘波动都比较大，说明其非线性比较严重。从辨识的角度来说，速度-力矩特性相对光滑使其更易于辨识。

图5 速度三角波30～80 r/min时的特性曲线

在固定负载情况下改变速度跟踪范围重复上述实验，可初步研究速度-力矩迟滞的变化情况。实验时负载固定为0.12 N·m，给定速度频率f为1.5 Hz，改变给定速度分别为：y=80+20sin(2πft)，y=80+28sin(2πft)，y=80+10sin(2πft)，测试结果如图6所示。从图6中可以看出，当速度变化范围变大时，迟滞范围也相应变大，但不是按照比例变化，有较强的非线性。速度变化区间缩小时，迟滞也相应缩小，但迟滞缩小的幅度较大，呈现明显的非线性。

图6 速度改变后的迟滞变化情况

通过改变频率可以测试频率-速度迟滞的变化情况。实验时电机驱动频率设定为42 000+1 500×sin(2πft)，其频率f为1.2 Hz，测试结果如图7、图8所示。频率设定值随时间变化如图7(a)所示，无负载时电机的速度特性如图7(b)所示，从图7(b)中可以看出，随着时间增加，电机谐振频率发生漂移，使得电机速度下降，这与文献[2-3]相吻合，其对应的频率-速度特性如图7(c)所示，由图7(c)可知，频率-速度呈现迟滞。电机驱动频率不变情况下带负载0.12 N·m重复上述实验，有负载时电机的速度特性如图8(a)所示，与7(b)类似，同样存在频率漂移现象，其对应的频率-速度特性如图8(b)所示，速度-力矩特性如图8(c)所示，频率-力矩特性如图8(d)所示。由于只控制驱动频率未对速度进行控制，同样频率下速度值随着时间增加会发生漂移，当负载变化时速度值也不同，因此只控制电机驱动频率而不对速度控制时，由于电机的频率漂移，其速度-频率、频率-力矩、速度-力矩特性产生偏差，导致迟滞也发生变化。

图7 无负载时频率跟踪特性曲线

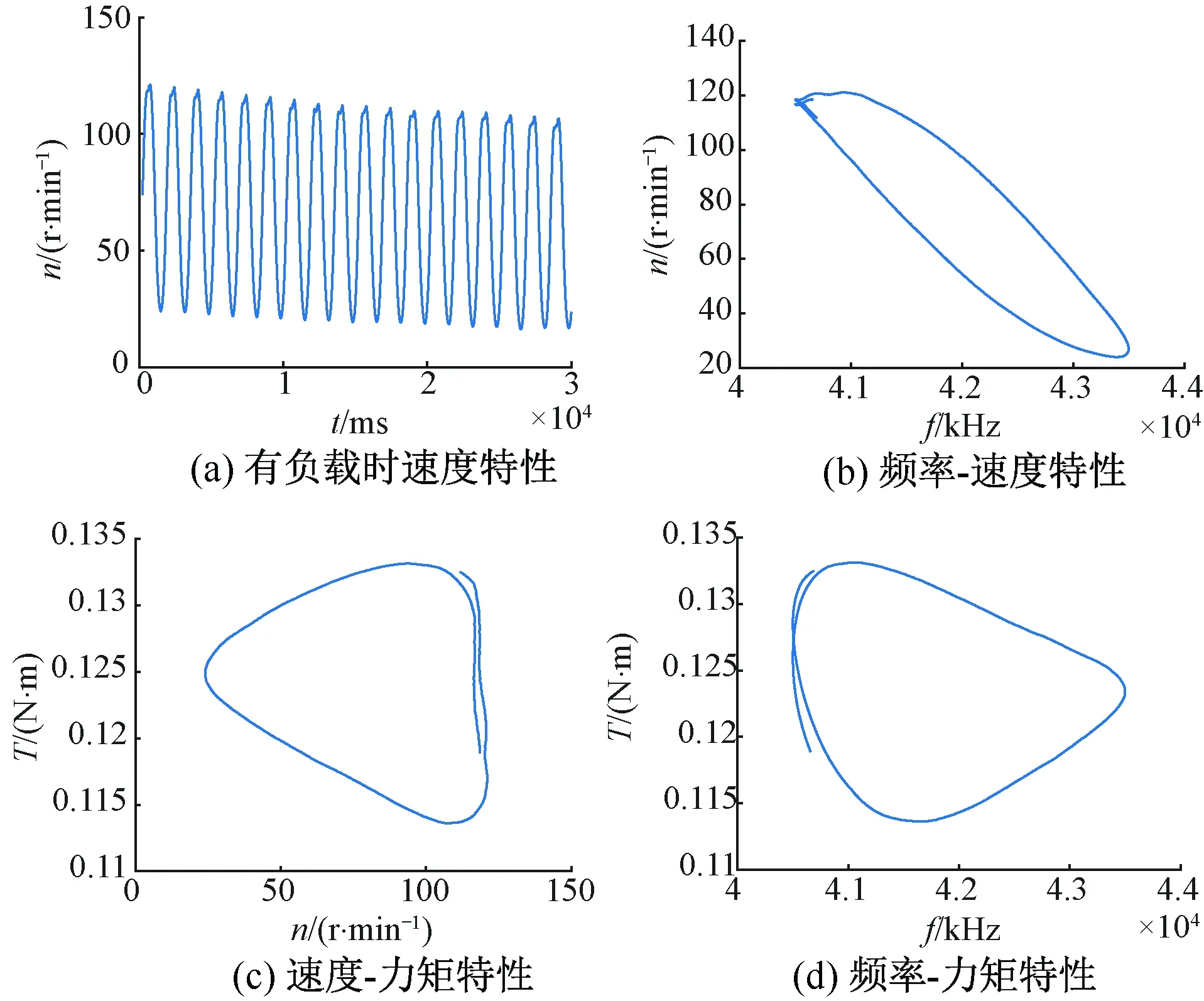
图8 有负载时频率跟踪特性曲线

综上所述，在测试力矩-频率、力矩-速度等特性时需要对电机的速度进行控制，频率是控制速度的一个变量。由实验结果可知，当使用频率调节时，其频率-速度特性边缘波动较大，导致辨识的准确性下降。本文使用电机速度调节时输出力矩和速度之间的迟滞，同样可以反映定子迟滞对电机输出力矩的影响。

2 递归神经网络的辨识算法

为了减小迟滞对电机控制系统的影响，需要先对迟滞进行辨识。本文引入递归神经网络(以下简称RNN)对其进行辨识，如图9所示。RNNI完成对超声波电机力矩-速度迟滞非线性的辨识。

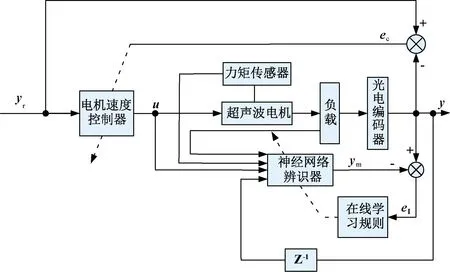
图9 RNN辨识系统结构图

RNNI由三层网络组成，分别是输入层、隐含层和输出层，如图10所示。辨识器输入信号为k-1时刻电机的速度信号和负载信号，通过神经网络辨识得到下一时刻电机的输出力矩，并与电机的实测数据进行比较，通过调整神经网络内部权重值，从而达到较好的辨识效果。

图10 RNNI结构图

(1)输入层

(1)

式中：x1(k)为k-1时刻电机的速度检测信号；x2(k)为k-1时刻电机的负载信号。

(2)

(2)隐含层

j=1,…，20

(3)

(4)

(3)输出层

(5)

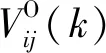
RNNI的输出ym(k)=[ym1(k)ym2(k)]T，其中ym1(k)为k时刻辨识模型的力矩值；ym2(k)为k时刻辨识模型的速度值。

(6)

定义RNNI的误差函数EI(k)：

(7)

(8)

(9)

(10)

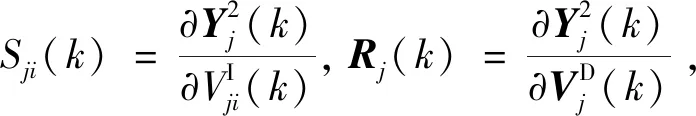
(11)

(12)

(13)

其中：

(14)

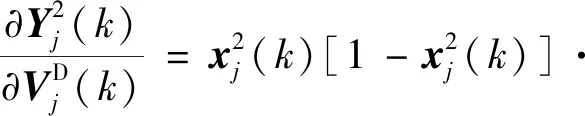
(15)

取离散型Lyapunov函数VI(k)：

(16)

同理可以证明，只要保证：

(17)

(18)

(19)

(20)

3 实验及结果分析

基于半实物仿真的超声波电机测控系统包括硬件平台和软件平台，其中硬件平台由仿真机系统和电机对拖平台两部分组成。仿真机包括机箱、CPU、板卡等，板卡主要实现AD、DA、PWM发生和脉冲计数等功能，完成测控过程的输入输出数据采集和转换。电机对拖平台如图11所示，平台由光电编码器、被测电机、力矩传感器、负载电机四部分组成。图10中，①为光电编码器；②为被测的超声波电机；③为力矩传感器；④为负载电机。我们搭建的半实物仿真平台使用量程为2 N·m的电机力矩传感器ZJ-2AM进行力矩测量，分辨率为3‰，可以满足力矩动态性能测控的要求。位置检测采用分辨率为10 000脉冲/转的光电编码器，可以实现电机速度的测量。超声波电机的型号为USR-60，其额定力矩为0.5 N·m，堵转力矩为1 N·m。负载电机型号为60LCB040C-J43A16，可通过输入电压控制输出力矩，其输出的最大力矩为1.27 N·m。整个测控系统的数据采样频率为1 kHz。

图11 电机对拖平台

电机转速、力矩、电压、负载等数据经过控制平台采集后，传送到PC机上显示与保存。PC机上运行基于RNN的辨识算法，将采集到的数据作为输入变量供RNN辨识算法进行运算，保存神经网络的输出结果，进行绘图并分析实验结果，实现对RNN辨识算法的验证。

为了预测超声波电机的力矩-速度迟滞特性，首先对RNNI进行训练。RNNI要用到的训练参数如下：

(1)损失函数

损失函数的作用是评估神经网络的准确度，函数的输入是神经网络的预测值和实测值，输出是它们的误差。在训练中损失函数采用均方误差函数MSE。MSE数值越小，说明神经网络模型误差越小，性能越好。MSE定义：

(2)训练集与测试集的构建

数据集由10组不同驱动信号和不同负载情况下的转速、力矩、电压等数据构成。负载分别设定为0.254 N·m、0.318 N·m、0.38 N·m、0.406 N·m。这些数据均在半实物仿真平台上采集得到，其中，8组数据作为训练集进行RNNI的训练，共有40 000条数据；2组数据作为测试集对RNNI进行测试，共有10 000条数据。

(3)标准化处理

在训练神经网络时，为了加速神经网络的训练和收敛速度，我们对数据集进行标准化处理，也就是对数据集进行归一化操作，将数据数值变换为0～1之间，变换关系如下：

式中：μ是均值；σ2是方差；Xin是输入数据；Xout是输出数据。选取跟踪给定速度y=180+30sin(9.42t)，负载0.254 N·m时的一组转速数据来显示标准化的效果。

通过计算图12(a)的原始数据，得到该组数据均值μ=181.644，方差σ2=548.853，代入标准化公式，可得到标准化处理后的转速曲线，如图12(b)所示。

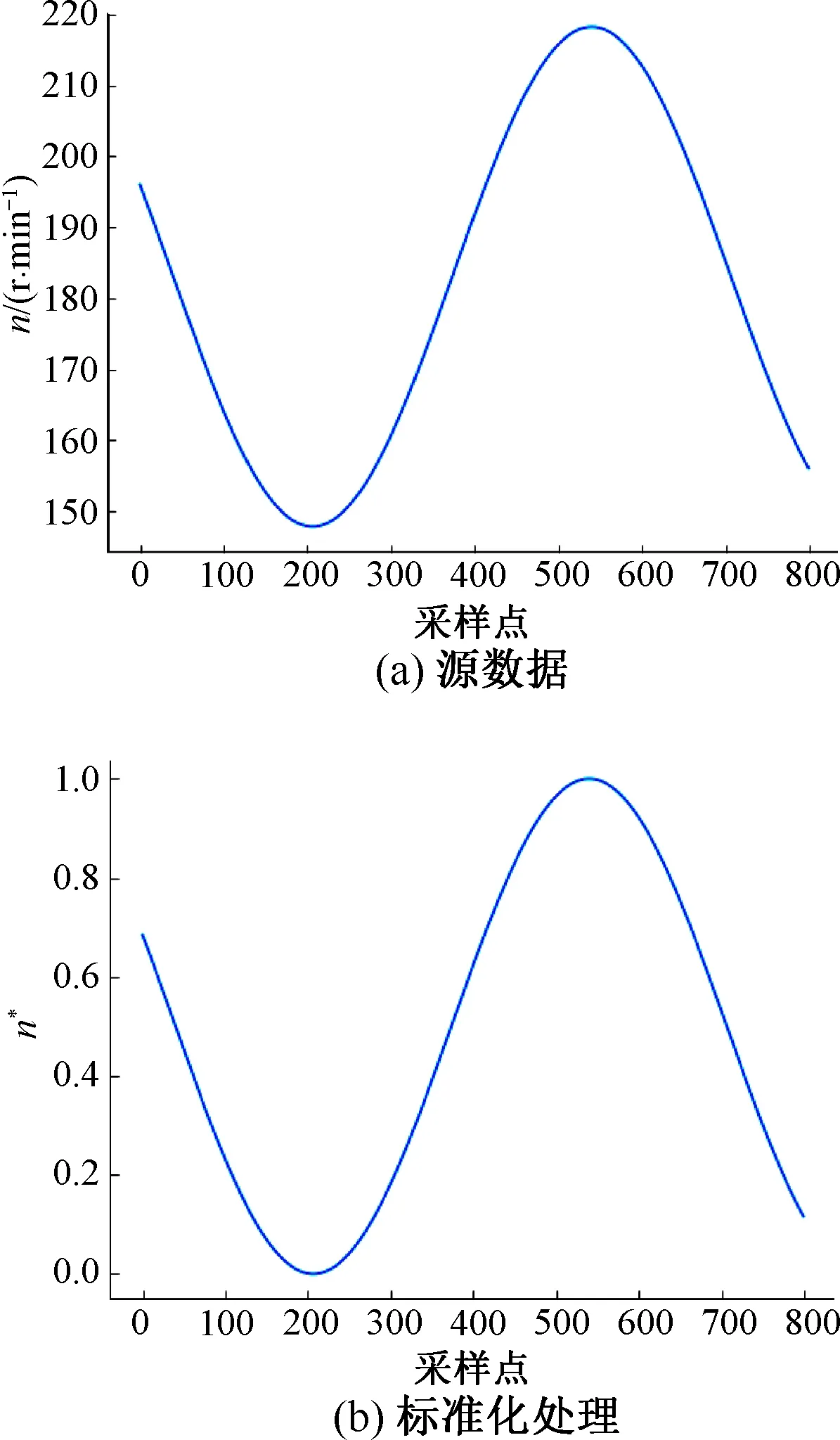
图12 标准化(归一化)处理

(4)网络参数

由图9的RNNI神经网络结构可知，输入层的神经元个数为2个，输出层的神经元个数为2个。我们使用反复训练和测试的方法来确定隐藏层神经元的个数。测试使用数据为跟踪给定速度y=180+30sin(9.42t) (一个周期约667个点)，负载0.254 N·m下的一部分转速数据，共有4 000条数据，并进行标准化处理，学习率设置为0.01，设置训练迭代1 000次。使用不同神经元个数进行训练的训练时间和均方误差MSE如表1所示。由表1可见，使用较少的神经元进行训练，虽然减少了训练所需时间，但降低了模型的拟合程度，误差变大，出现了欠拟合的问题；使用较多的神经元进行训练，不仅训练时间变长，而且误差变大，出现了过拟合的问题。由实验结果可知，如果设定隐藏层的神经元个数为20个，可以在较短的时间内达到较好的训练效率和拟合准确度。

表1 不同神经元个数下的MSE和训练时间

对于学习率的确定，我们也使用同样的方法，实验中只改变学习率而其他参数不变。使用不同学习率进行训练的时间和均方误差MSE结果如表2所示。

表2 不同学习率的MSE和训练时间

由表2可见，使用较小的学习率进行训练，误差较小，但训练时间变长；使用较大的学习率，虽然训练时间减少，但会导致误差增大，甚至导致网络无法收敛。当学习率分别使用0.001和0.01时，神经网络的误差比较接近，我们选择训练时间较少的学习率0.01来训练神经网络。

(5)训练过程

在准备好数据集并设置好网络参数后，就可以对RNNI进行训练。RNNI的输入是电机的转速与输出力矩，输出是预测的电机转速与力矩。RNNI的训练流程如下：设置好的网络各项参数，设置迭代计算的次数，网络权重使用随机初始化。第一步是通过神经网络输入数据，神经网络计算得到预测值；第二步是计算相应的损失函数；第三步是利用反向传播算法对网络的权重进行修正。重复上述过程，当迭代到最大次数时停止模型训练。

我们分别在负载0.254 N·m、0.318 N·m、0.38 N·m、0.406 N·m的情况下对数据进行训练，迭代次数设置为1 000。表3显示了不同负载情况下的模型收敛情况与误差。RNNI的训练损失值变化曲线如图13所示。从图13可以看出，在不同负载下模型收敛情况良好，误差较小，没有发生过拟合或欠拟合的问题。由训练结果可知，负载越小，网络收敛得越快。

表3 不同负载下的训练结果

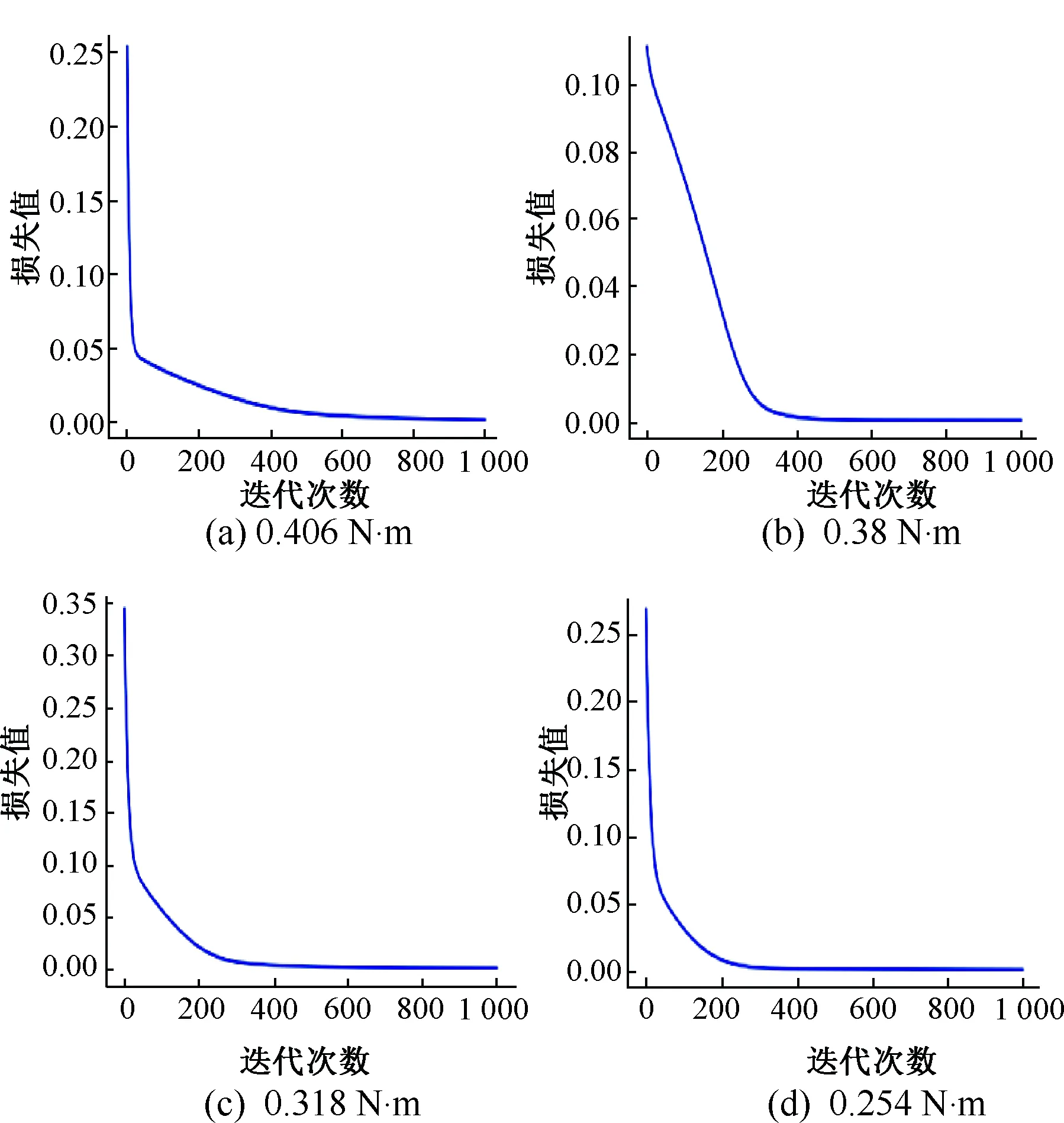
图13 不同负载下的损失值变化曲线

RNNI的目的是实现超声波电机力矩-速度迟滞非线性的辨识。模型训练结束后，为了验证RNNI的有效性，观察RNNI在不同负载情况下迟滞曲线的辨识效果来验证辨识器的性能。同时，通过绘制绝对误差曲线来观察辨识过程中的误差变化情况，并通过计算平均绝对误差来评估辨识的效果。平均绝对误差MAE定义：

接着对不同负载的迟滞曲线进行辨识，下面以负载0.318 N·m加以说明，其他负载时情况类似，对辨识器验证时给定跟踪速度不变。

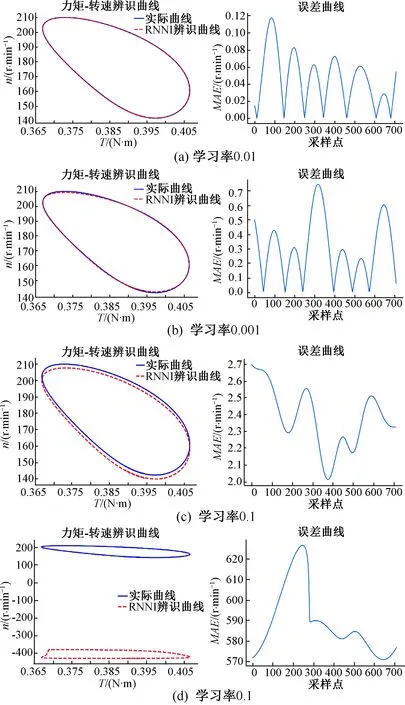
图14 负载0.318 N·m时辨识结果和误差

图14是负载为0.318 N·m，学习率为0.001、0.01、0.1与1的辨识结果和误差，由图14的辨识结果可知，学习率为0.01和0.001时，RNNI都可以较准确地对电机的迟滞情况进行辨识且误差较小，可见负载对RNNI的收敛影响不大，RNNI的抗负载干扰能力较强。另外，学习率为0.01、0.001时辨识误差分布基本没有规律，在一个周期的起始点和终止点的辨识误差不大，在一个周期的其他区间段出现误差峰值。学习率为1时辨识误差非常大，基本没有达到辨识目的。在其他负载情况下都有上述类似的情况出现。

不同负载下的辨识误差如表4所示。从表4负载与学习率的关系可以看出：学习率为0.01、0.001而负载不同时，辨识误差基本随着负载的减小而增大；同样负载条件下学习率为0.01时辨识误差最小，在不同负载下学习率为0.001时辨识误差比0.01略大，学习率为0.1时的辨识误差比0.01和0.001时大很多，学习率为1时辨识效果较差。综上所述，选择学习率为0.01时辨识效果较好。

表4 不同负载下的辨识误差MAE (r·min-1)

总之，通过合理选择RNNI网络参数，并对比表1～表4结果可以知道，对电机迟滞的辨识可以达到MSE小于6×10-4，不同负载下辨识误差小于0.11，可以实现对力矩-速度迟滞的有效辨识。

4 结 语

本文以LCC驱动电路为基础，针对不同条件下超声波电机的速度-力矩迟滞，使用RNNI对电机迟滞进行辨识，得到相应的辨识算法，然后通过实验加以验证。由实验结果可知，当参数选择合适的情况下RNNI对不同负载下的超声波电机速度-力矩迟滞辨识效果较好。