一种基于轻量级堆叠沙漏网络的机械臂姿态估计方法

王 琦,郑飂默,王诗宇,刘信君,郭 威

1(中国科学院大学,北京 100049)2(中国科学院 沈阳计算技术研究所,沈阳 110168)3(沈阳中科数控技术股份有限公司,沈阳 110168)4(盐城师范学院 信息工程学院,江苏 盐城 224002)

1 引 言

精准而灵活的机械臂在工业制造领域中有着广泛的应用,机械臂能够执行装配作业、物体抓取、人机交互、碰撞检测等任务[1].近年来,基于视觉的机械臂控制受到了越来越多的关注,与使用特定传感器的传统系统相比,视觉系统具有更大的信息量,更加灵活,能够适应复杂多样的任务[2,3].基于视觉的机械臂控制系统[4,5]能够根据视觉信息对机械臂进行控制,并且可以进一步地实现机械臂的抓取[6,7].而如果我们想对机械臂进行控制,首先就要知道机械臂各个关节的位置,即机械臂的姿态,因此机械臂的姿态估计是机械臂进行控制必不可少的一步,对于机械臂控制系统的实现至关重要.

在实际的机械臂应用中,机械臂所能提供的存储资源和计算资源有限,机械臂的姿态估计不仅需要模型有较高的精度,还要求模型具有较小的参数量和计算量.因此,在机械臂姿态估计的过程中,如何减少模型的参数量和计算量是一个非常重要且现实的研究课题.

针对机械臂的姿态估计问题,学术界已经开展了相关的研究工作.Zuo等人[8]使用3D模型生成了大量的虚拟数据,在此虚拟领域中训练视觉模型,并在领域自适应后应用于真实世界的图像.此外,其设计了一种半监督方法,该方法充分利用了关键点之间的几何约束,使用迭代算法进行优化.Lee等人[1]提出了一种从单个图像估计机械臂姿态的方法,其使用深度神经网络来处理RGB图像来检测机械臂上的关键点,并且使用域随机化完全在模拟数据上进行网络的训练.Widmaier等人[9]使用机械臂的深度图像作为输入来直接估计角关节的位置.其使用了一个随机回归森林来进行估计,该模型使用合成生成的数据进行训练.Tremblay等人[10]使用RGB图像作为神经网络的输入,并在虚拟数据上训练神经网络,通过领域随机化来弥补虚拟和真实的差距,该神经网络还会执行在线的相机标定来更精准地估计机械臂的姿态.Bohg等人[11]使用随机决策森林来分割机械臂之间的连接,并使用标注好的深度图像进行训练,从而来估计机械臂真实关节的位置.尽管上述算法的精度很高,但这些方法仍存在参数量和计算量过大等不足.现有方法往往通过牺牲模型效率来换取精度优势,精度越高的方法所需要的计算开销也越大.在云上部署这些高精度模型会很困难,庞大的参数量也限制了模型在资源受限设备(比如机械臂、手机等设备)上的部署.这些高精度模型需要巨大的计算开销和内存开销,严重阻碍了资源受限情况下的使用.

针对现有研究中缺乏通用的模型轻量化方法以及轻量级模型会面临的性能退化问题,本文以堆叠沙漏网络为基础,构建了具有两个堆的堆叠沙漏网络,并使用了一种全新的神经网络基本单元Ghost模块来替代堆叠沙漏网络中的标准卷积,从而搭建出轻量级的机械臂姿态估计神经网络,即Ghost-SHN(Ghost Module-Based Stacked Hourglass Network).Ghost-SHN在保留模型泛化性能的前提下改善机械臂姿态估计模型的推理效率,能够更好地在机械臂上进行部署,实现了轻量级的机械臂姿态估计.

2 相关理论

2.1 堆叠沙漏网络

堆叠沙漏网络(Stacked Hourglass Network,SHN)[12]是由Newell等人提出的用于姿态估计的神经网络.基于这种网络结构的人体姿态识别方法获得了 MPII 2016 竞赛的冠军.

SHN由多个堆叠起来的沙漏模块(Hourglass Module)组成.类似Inception[13]的残差块(Residual Block)组成了沙漏模块.

沙漏模块主要由下采样与上采样操作构成.下采样是通过卷积及池化操作实现的,以获得分辨率较低的特征图,降低计算复杂度.之后通过最近邻插值法(Nearest Interpolation)进行上采样,使图像特征的分辨率提高.此外,直连边(Shortcut Connection)可以向该模块的后半部传递所有分辨率的特征.该网络结构提取的特征融合了多尺度及上下文信息,具有较强的预测物体位置的能力.

相较于其他姿态估计方法,SHN拥有更加简明且易于扩展的结构,并且更加准确高效.

2.2 模型压缩方法

因为SHN之类的神经网络模型又大又慢,所以将其部署到机械臂等资源受限设备很困难.因此,学者们提出了一些模型的压缩方法,比如剪枝[14]、量化[15]、知识蒸馏[16,17]等;还有一些研究则致力于紧致的网络结构设计,比如MobileNet[18]和ShuffleNet[19]就是两个非常经典的紧致网络结构.

MobileNet将普通卷积替换为深度可分离卷积(Depthwise Separable Convolution,DSC).深度可分离卷积通过深度卷积(Depthwise Convolution)和卷积这两个操作来实现,从而实现了网络的轻量化.

由于MobileNet中大量使用1×1卷积,为了得到更加轻量级的网络,ShuffleNet将1×1卷积替换为组卷积并引入通道打乱(Channel Shuffle),从而在加快速度的同时保证模型的精度.

除了上述经典的模型压缩方法外,Han等人[20]提出了一种新颖的Ghost模块,其可以使用更少的参数来生成更多特征图,并且与普通卷积相比,在输出特征图大小不变的情况下,Ghost模块中所需的参数量和计算量都有一定程度的减少.

在本文4.3节“实验过程与结果分析”中,我们将分别采用MobileNet和ShuffleNet中使用的方法来对堆叠沙漏网络进行模型压缩,并与本文提出的模型进行对比.

3 轻量级机械臂姿态估计

由SHN的网络结构可知,SHN使用了大量的卷积,但这些卷积会占据大量的参数量和计算量,这给机械臂姿态估计模型在机械臂上的部署带来了挑战.为了减少SHN的参数量与计算量,本文引入了Ghost模块,提出了一种新的基于Ghost模块的堆叠沙漏网络,简称为Ghost-SHN.Ghost-SHN以SHN为基础,通过替换SHN的普通卷积为Ghost模块,有效地减少了模型的参数量和计算量.

3.1 基于Ghost模块的堆叠沙漏网络

Ghost-SHN用来检测机械臂的关键点,其输入是机械臂的图像,输出是机械臂图像的热图(Heatmap),并将热图中响应值较大的区域视为关键点,每个关键点对应一个热图.Ghost-SHN由两个沙漏模块组成,每个沙漏模块由多个残差块组成,每个残差块的卷积被替换为Ghost模块,其结构如图1所示.下面具体介绍下Ghost-SHN中单个沙漏模块以及沙漏模块中残差块的结构.

图1 Ghost-SHN网络结构

Ghost-SHN的单个沙漏模块用来捕捉机械臂各个尺度的信息,其结构如图2所示.在沙漏模块中,特征图(Feature Map)的计算可分为两个阶段:自顶向下(Top-Down)阶段和自底向上(Bottom-Up)阶段.在自顶向下阶段中,沙漏模块使用Ghost模块和池化操作(Pooling Operation)进行下采样.当特征图的分辨率达到最低的时候,沙漏模块开始自底向上阶段.在自底向上阶段,沙漏模块采用最近邻插值来进行上采样,并且通过直连边把较高分辨率的特征图拿过来,再将这两部分特征按元素位置进行相加(Elementwise Addition),因此沙漏模块能够提取多尺度特征.

图2 单个沙漏模块的结构

图2中的方块是残差块,残差块中的特征映射可分为残差映射(Residual Mapping)和恒等映射(Identity Mapping).我们将组成单个沙漏模块的残差块中的普通卷积替换成Ghost模块(除了1×1卷积).因此残差块包括了一个Ghost模块和两个1×1卷积,其具体结构如图3所示.

图3 残差块结构

假设输入的数据为X′∈c′×h′×w′,其中c′是输入数据的通道数,h′和w′分别是输入数据的高度和宽度.假设要输出m个特征图,SHN使用的是的p×p卷积,则计算过程如式(1)所示.

Y′=X′*W

(1)

其中*是卷积运算,W∈c′×p×p×m是这一层中的卷积核,Y′∈h″×w″×m是具有m个通道的输出特征图,h″和w″分别是输出数据的高度和宽度.

Ghost-SHN中使用的是Ghost模块,Ghost模块使用一次卷积(Primary Convolution)来生成n个原始特征图,一次卷积与普通卷积的超参数相同,其计算过程如式(2)所示.

Y″=X′*W′

(2)

其中W′∈c′×p×p×n是卷积核,n≤m.接着,本文对每个原始特征使用线性运算来生成k个幻影特征图,具体计算过程如式(3)所示.

(3)

(4)

因为线性运算g在每个通道上执行,所以其计算量比普通卷积少得多.

3.2 模型复杂度分析

接下来,本文分析下Ghost-SHN的模型复杂度.首先对比下SHN和Ghost-SHN的参数量,假设β为SHN中d个p×p卷积参数所占的内存开销,β*为Ghost-SHN中d个Ghost模块所占的内存开销,则模型参数的压缩比Cr的计算如式(5)所示.

(5)

其中a×a的大小与p×p相似,k远小于c.Ghost模块有一个恒等映射和m/k(k-1)个线性运算,每个线性运算的平均核大小为a×a.

接着对比下SHN和Ghost-SHN的计算量,假设λ为SHN中d个p×p卷积的计算开销,λ*为Ghost-SHN中d个Ghost模块的计算开销,则模型的计算量比Sr的计算如式(6)所示.

Sr(SHN,Ghost-SHN)=

(6)

由式(5)和式(6)可知,堆叠沙漏网络使用了大量的普通卷积操作,其设计存在一定的冗余性.Ghost-SHN使用Ghost模块替代SHN中的普通卷积,可以较好地减少SHN的参数量和计算量.

4 实 验

4.1 实验环境

实验服务器的操作系统为 Ubuntu 18.04,配置有Intel Core i9-10920X 3.5 GHz CPU和 9.7 G 显存的 RTX 3080 显卡.模型使用深度学习框架 PyTorch 来实现.

实验使用的是 OWI-535机械臂,如图4所示,该机械臂有4个关节和17个关键点.4个关节分别称为旋转、底座、肘部和腕部.每个关节上都有1个电机,4个电机的运动范围分别为 270度、180度、300度和120度.

图4 OWI-535 机械臂结构

4.2 实验数据集

本文使用文献[8]中的4个数据集进行模型的训练和测试.

第1个数据集是虚拟数据集,该数据集里面有用虚幻引擎 4 生成的 5000 张虚拟图像.其中,4500 张用于训练,其余 500 张用于测试.

第2个数据集是实验室数据集,该数据集包含了 720P 摄像头拍摄的428张图片.图片中有一些干扰因素,比如彩色的盒子、骰子等,这增加了数据集的难度.

第3个数据集是YouTube 数据集,其中的图片从 YouTube 上抓取的.图片类型多样,图片中的机械臂可能被修改,几何约束条件可能不完全成立.YouTube 数据集里面有 275 张图片,里面标注了每个二维关键点的可见性以及位置.

第4个数据集是第3个数据集的子集,仅考虑YouTube数据集中关键点可见的图片,本文称其为YouTube(可见)数据集.

3个数据集的图像示例如图5所示,第1行是虚拟数据集,第2行是实验室数据集,第3行是 YouTube 数据集.

图5 3个数据集的图像示例

4.3 实验过程与结果分析

首先进行关键点的检测,将输入的机械臂图像裁剪为256×256并将其传送到具有两个堆的Ghost-SHN.Ghost-SHN生成了17 个热图,每个热图的大小为64×64,对应着一个关键点.在模型训练时,本文使用了数据增强技术,对裁剪后的图像进行随机平移、旋转、缩放、色彩转换和翻转.本文使用RMSProp优化器来优化网络,学习率为2.5×10-4,损失函数为均方误差函数,每一批输入网络的样本个数为6,对于本文使用的4个数据集,Ghost-SHN训练 30个epoch.

在上述关键点检测的步骤中,本文通过Ghost-SHN进行关键点的检测,网络的输出是与17个关键点对应的17个通道的热图.在预测时,本文取热图上响应最明显的位置作为预测结果.关键点检测结果的示意图如图6所示.

图6 关键点检测结果

获取了二维关键点的位置后,本文进行三维还原,将机械臂建模为一个4个自由度的多刚体模型,因此17个关键点的位置满足一定的约束关系(比如两个关节之间的长度).在透视投影的假设下,每个关键点都是三维坐标的二维投影,因此可以写成如式(7)所示的方程:

[y|1]T·S=K·[R|t]·[z|1]T

(7)

其中y是二维坐标矩阵,z是三维坐标矩阵,1是全一向量,K是相机的内参矩阵,S是缩放向量,R是旋转矩阵,t是平移向量.本文通过解如式(7)所示的线性方程,就可以得到关键点的三维坐标,进一步地,本文可以根据几何约束关系来获得机械臂各转轴的角度.

为了验证本文算法的有效性,本文分别实现了DSC-SHN(基于深度可分离卷积的堆叠沙漏网络)以及Shuffle-SHN(基于组卷积和通道重排的堆叠沙漏网络).接下来对Ghost-SHN、SHN、DSC-SHN和Shuffle-SHN这4个算法的性能进行对比评估.

为了评估关键点检测的精度,本文把预测关键点和真正的关键点之间的距离与阈值τ进行比较,如果在阈值τ内,就认为预测关键点是正确定位的关键点,本文使用正确定位的关键点的百分比(Percentage of Correct Keypoints,PCK)作为度量指标.具体地,令τ=0.2,即使用PCK@0.2来衡量关键点检测的精度.PCK@0.2是指当阈值为0.2时,正确定位的关键点的百分比.二维关键点检测的结果如表1所示.

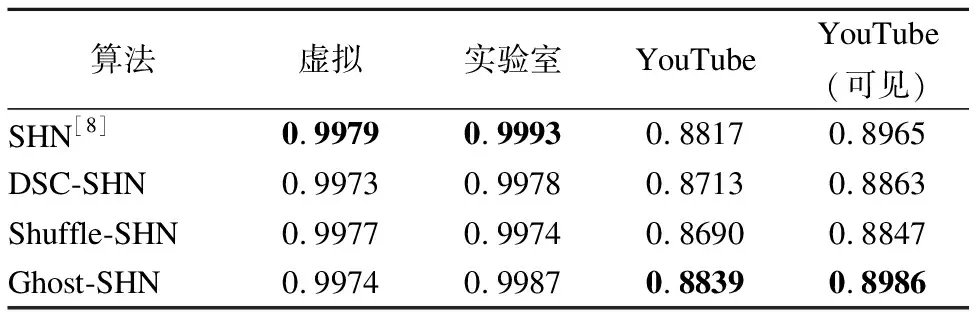
表1 4个数据集上的二维关键点检测正确率

本文还在真实图像上测试模型的三维姿态估计性能.本文仅针对实验室数据集来进行定量的 三维姿势估计,因为很难获取YouTube 数据集的三维标注.三维姿态估计的结果如表2所示.

表2 实验室数据集上的三维姿态估计误差(角度)

接下来,计算各个模型在4个数据集上的参数量与计算量.参照文献[20],本文使用浮点运算量(FLoating point OPerations,FLOPs)来衡量模型的计算量.具体来说,实验中使用的是GFLOPs,即109FLOPs.不同模型参数量的对比结果如图7所示,不同模型计算量的对比结果如图8所示.由于事先将输入图像裁剪成256×256,所以同一个模型在4个数据集上的参数量和计算量都是一样的.

最后,本文综合对比下各个算法.如表1所示,Ghost-SHN在 YouTube数据集和 YouTube(可见)数据集的精度是最高的,因此Ghost-SHN的泛化性能很好.如表2所示,Ghost-SHN在3个关节上的预测误差以及平均预测误差比SHN小.此外,如图7所示,SHN的参数量是Ghost-SHN的1.49倍.如图8所示,SHN的计算量是Ghost-SHN的1.42倍.虽然DSC-SHN 的参数量和计算量比Ghost-SHN更小,但其在4个数据集上的精度都不如Ghost-SHN高.这就是说,DSC-SHN虽然具有较低参数量与计算开销,但模型的泛化能力也同时发生了退化.而Ghost-SHN提升了模型的泛化能力,其在精度、参数量、计算量三者之间取得了一个较好的权衡.

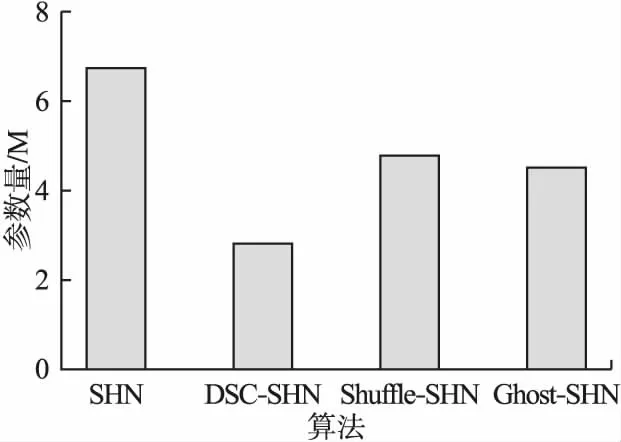
图7 不同算法参数量对比

图8 不同算法FLOPs对比

5 总 结

在实际的应用中,机械臂的姿态估计不仅需要模型有较高的精度,还要求模型具有较小的参数量和计算量.为此,本文分析了传统的机械臂姿态估计算法在参数量和计算量上的不足,提出一种基于Ghost模块的堆叠沙漏网络,即Ghost-SHN.Ghost-SHN以SHN基础,将SHN中的普通卷积替换成轻量的Ghost模块,从而实现了模型的压缩.4个典型数据集上的实验结果表明,Ghost-SHN不仅继承了SHN泛化性能好的优点,而且模型的参数量和计算量大大减少.Ghost-SHN在参数量、计算量和精度三者之间取得了较好的权衡,能够更好地在机械臂上进行部署,实现了轻量级的机械臂姿态估计.